Helmert transformation

The transformation from a reference frame 1 to a reference frame 2 can be described with three shifts Δx, Δy, Δz, three angles of rotation Rx, Ry, Rz and a scale factor μ

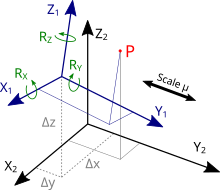
The Helmert transformation (after Friedrich Robert Helmert , 1843-1917), also called 7-parameter transformation , is a coordinate transformation for three-dimensional Cartesian coordinates , which is often used in geodesy for the distortion- free conversion from one to another, likewise three-dimensional system becomes:

${\displaystyle X_{T}=C+\mu RX}$

• ${\displaystyle X_{T}}$ ... transformed vector
• ${\displaystyle X}$ ... output vector

The seven parameters are:

• ${\displaystyle C}$... displacement vector. Contains the three shifts along the coordinate axes
• ${\displaystyle \mu }$... scale factor
• ${\displaystyle R}$... rotation matrix. Consists of three angles of rotation ( rotations around the coordinate axes ) r _x , r _y , r _z . The rotation matrix is ​​an orthogonal matrix .

The Helmert transformation is thus a similarity transformation . It is a specialization of the Galileo transformations , which include affine and projective transformations ; the latter, however, distort the length of the route.

Calculation of the parameters

If the transformation parameters are unknown, they can be calculated using identical points (i.e. points whose coordinates are known before and after the transformation). Since a total of 7 parameters (3 shifts, 1 scale, 3 rotations) have to be determined, at least 2 points and one coordinate of a 3rd point (e.g. the z coordinate) must be known. This creates a system of equations with seven equations and just as many unknowns that can be solved.

In practice, more points are usually used. This overdetermination gives you, firstly, a check on the correctness of the points used and, secondly, the possibility of a statistical assessment of the result. In this case, the calculation is carried out using a compensation calculation using the Gaussian method of least squares .

In order to obtain numerically favorable values ​​for the calculation of the transformation parameters, the calculations are carried out with coordinate differences based on the mean value of the given points.

Two-dimensional case

A special case is the two-dimensional Helmert transformation for plane coordinate systems . It is used u. a. in geodesy , when a small-scale surveying network with overdetermination is connected to the national coordinate system, or in astrometry for simple plate reduction with well-dimensional photo plates. The transformation corresponds to a rotational stretching with parallel displacement in any direction.

Instead of 7, it only requires 4 transformation parameters , namely 2 shifts, 1 scale factor and 1 rotation. The calculation of these 4 parameters requires two identical points in the two coordinate systems; if more points are given, an adjustment is made again.

application

The Helmert transformation is used in geodesy , among other things , to transform coordinates of points from one coordinate system to another. So z. B. the conversion of points of the regional land survey into the WGS84 used for GPS -locations possible.

The Gauss-Krüger coordinates plus the height are converted into 3D values ​​step by step: ${\displaystyle x,y}$ ${\displaystyle H}$

1. Calculation of the ellipsoidal latitude, longitude and height ( ) ${\displaystyle B,L,H}$
2. Calculation of the reference ellipsoid of the national survey ${\displaystyle X,Y,Z}$
3. 7-parameter transformation (which changes almost uniformly by a maximum of a few hundred meters and the distances by a few mm per km). ${\displaystyle X,Y,Z}$
4. Inverse transformation into ellipsoidal latitude, longitude and height

This enables terrestrially measured positions to be compared with GPS data; the latter can - transformed in the reverse order - be introduced as new points in the national survey.

The third step (the Helmert transformation) consists in the application of a rotation matrix , the multiplication with a scale factor (µ is close to the value 1) and the addition of a shift . ${\displaystyle \mu =1+m/10^{6}}$ ${\displaystyle C}$

Since the sub-operations of this transformation all cause only small changes, the coordinates of a reference system can be derived from the reference system using the following formula : ${\displaystyle B}$ ${\displaystyle A}$

${\displaystyle {\begin{bmatrix}X\\Y\\Z\end{bmatrix}}^{B}={\begin{bmatrix}c_{x}\\c_{y}\\c_{z}\end{bmatrix}}+\mu \cdot {\begin{bmatrix}1&r_{z}&-r_{y}\\-r_{z}&1&r_{x}\\r_{y}&-r_{x}&1\end{bmatrix}}\cdot {\begin{bmatrix}X\\Y\\Z\end{bmatrix}}^{A}}$

where the angles of rotation , and are to be used with their value in radians. ${\displaystyle r_{x}}$ ${\displaystyle r_{y}}$ ${\displaystyle r_{z}}$

Or for each individual component:

${\displaystyle {\begin{aligned}&X_{B}=c_{x}+\mu \cdot (X_{A}+r_{z}\cdot Y_{A}-r_{y}\cdot Z_{A})\\&Y_{B}=c_{y}+\mu \cdot (-r_{z}\cdot X_{A}+Y_{A}+r_{x}\cdot Z_{A})\\&Z_{B}=c_{z}+\mu \cdot (r_{y}\cdot X_{A}-r_{x}\cdot Y_{A}+Z_{A})\\\end{aligned}}}$

For the reverse transformation, all parameters are multiplied by −1.

The 7 parameters are determined for the respective region (separate survey , federal state, etc.) with 3 or more "identical points" of both systems. In the event of overdetermination, the small contradictions (usually only a few cm) are balanced out using the least squares method - that is, eliminated in the most statistically plausible way.

Standard parameter sets

area	Starting system	Target system	c x (meters)	c y (meters)	c z (meters)	m ( ppm )	r x ( arcsecond )	r y ( arcsecond )	r z ( arcsecond )
England , Scotland , Wales	WGS84	OSGB36	−446.448	125.157	−542.06	20.4894	0.1502	0.247	0.8421
Ireland		Ireland 1965	−482.53	130.596	−564.557	−8.15	−1.042	−0.214	−0.631
Germany		DHDN / Potsdam 2001	−598.1	−73.7	−418.2	−6.7	0.202	0.045	−2.455
		Pulkowo S42 / 83 2001	−24.9	126.4	93.2	−1.01	−0.063	−0.247	−0.041
Austria (BEV)		MGI	−577.326	−90.129	−463.919	−2.423	5.137	1.474	5.297
Switzerland		LV95	−674.374	−15,056	−405.346	0	0	0	0
United States		Clarke 1866	8th	−160	−176	0	0	0	0

The examples are standard parameter sets for the 7-parameter transformation (or: datum transformation) between two ellipsoids. For the transformation in the opposite direction, the sign must be changed for all parameters . The angles of rotation , and are sometimes referred to as κ, φ and ω. The datum transformation from WGS84 to Bessel is interesting for Central Europe insofar as GPS technology refers to the WGS84 ellipsoid, whereas the Gauß-Krüger coordinate system used in Germany and Austria is usually based on the Bessel ellipsoid. ${\displaystyle r_{x}}$ ${\displaystyle r_{y}}$ ${\displaystyle r_{z}}$

Since the earth does not have a perfect ellipsoid shape, but is described as a geoid , the standard parameter set is not sufficient for a datum transformation with measuring accuracy. Instead, the geoid shape of the earth is described by a multitude of ellipsoids. Depending on the actual location, the parameters of the "locally best-matching ellipsoid" are used. These values ​​can deviate significantly from the standard values ​​and usually lead to significant changes in the result in the transformation calculation.

restrictions

Since the Helmert transformation only knows one scale factor, it cannot be used as a similarity transformation for:

• The equalization of measurement images or photos , here is a projective transformation or photogrammetric rectification apply;
• The adjustment of a paper distortion when scanning old plans and maps . In these cases an affine transformation should be used.

See also

• Reference system , Global Positioning System , Galileo
• Engineering geodesy , photogrammetry

Web links

• Quaternion transformation to determine the 7 parameters of a spatial Helmert transformation (online calculator)
• helmparms3d Determination of the 7 parameters of a 3d Helmert transformation (#c Library)
• w-volk.de
• Stefan A. Voser: Geometric Requirements for Data Exchange 1996
• Parameter values ​​of the Helmert transformation DHDN to ETRS89