Kiss number

In geometry , the -th kiss number (also contact number ) is the maximum number of one - dimensional unit spheres ( spheres with radius 1). which at the same time can touch another such unit sphere in Euclidean space without overlapping. Of lattice kiss numbers is when the centers of the balls in a grid are arranged. A known kiss number problem is the lack of a general formula to calculate kiss numbers. ${\ displaystyle n}$ ${\ displaystyle n}$

Kiss numbers in different dimensions

The kiss number for the first dimension is 2.

The kiss number for the second dimension is 6.

${\ displaystyle \ mathbf {n = 1}}$ : In one dimension the unit sphere is not a sphere, but a segment whose endpoints are 1 from the origin . Here, a further line can be added to both end points so that the kiss number for one dimension is obviously 2.

${\ displaystyle \ mathbf {n = 2}}$ : In the second dimension , the unit sphere is not a sphere, but a circle with radius 1. The problem of determining the kiss number in this dimension corresponds to the task of arranging as many coins as possible so that they all touch a central coin of the same size. It is easy to see (and prove) that the kiss number for the second dimension is 6.

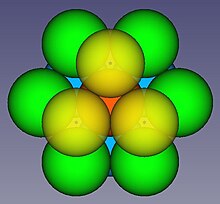
${\ displaystyle \ mathbf {n = 3}}$ : In the third dimension , finding the kiss number is not that easy; see. the graphic on the right. It is easy to arrange twelve spheres so that they touch the central sphere (for example, so that their centers form the corners of a cuboctahedron ). But you can still see a lot of empty space between the spheres and wonder whether a thirteenth sphere can be added. This problem was the subject of a famous argument between Isaac Newton and the mathematician David Gregory , which they led in 1692 over the Kepler conjecture . Newton said the maximum was twelve, Gregory said it was thirteen. In the 19th century, the first publications claiming to contain evidence for Newton's claim appeared. However, by today's standards, formal evidence was not provided until 1953 by Kurt Schütte and Bartel Leendert van der Waerden and in 1956 by John Leech .

${\ displaystyle \ mathbf {n = 4}}$ : It was only at the beginning of the 21st century that it was proven that the kiss number for the fourth dimension is 24.

${\ displaystyle \ mathbf {n> 4}}$ : Furthermore, the kiss numbers for the dimensions n = 8 (240) and n = 24 (196,560) are known; in the 24-dimensional space the balls are placed on the points of the leech grid so that there is no space left. The exact kiss numbers for dimensions 8 and 24 were determined independently in 1979 by Andrew M. Odlyzko and Neil JA Sloane or Vladimir Levenshtein.

The following table shows the known limits for the number of kisses up to dimension 24.

Kiss numbers in dimensions 1-12
dimension	Kiss number
dimension	lower limit	upper limit
1	2
2	6th
3	12
4th	24
5	40	44
6th	72	78
7th	126	134
8th	240
9	306	364
10	500	554
11	582	870
12	840	1,357

The kiss number for the third dimension is 12.
The central ball (red) is touched by
6 balls (green) in the same plane,
3 balls (yellow) above and
3 balls (blue, rotated 60 ° against yellow) below.

The exponential growth in the number of kisses; Dimensions 1 to 24. The gray area is limited by the upper and lower limits (see table).

Kiss numbers in dimensions 13-24
dimension	Kiss number
dimension	lower limit	upper limit
13	1,154	2,069
14th	1,606	3,183
15th	2,564	4,866
16	4,320	7,355
17th	5,346	11,072
18th	7,398	16,572
19th	10,688	24,812
20th	17,400	36,764
21st	27,720	54,584
22nd	49,896	82,340
23	93,150	124,416
24	196,560

Estimates show that the growth in kiss numbers is exponential ; see. Graphic next to the table. The basis of exponential growth is unknown.

Little is known about the kiss numbers in even higher dimensions; lower bounds are known for the dimensions (276.032), (438.872), (991.792), (2.948.552), (331.737.984) and (1.368.532.064). ${\ displaystyle n = 32}$ ${\ displaystyle 36}$ ${\ displaystyle 40}$ ${\ displaystyle 44}$ ${\ displaystyle 64}$ ${\ displaystyle 80}$

Lattice kiss numbers in different dimensions

The exact grid kiss numbers are known for the dimensions 1 to 9 and 24. The following table shows the lattice kiss numbers and the known lower limits up to dimension 24:

Lattice kiss numbers in dimensions 1-12
dimension	Lattice kiss number
1	2
2	6th
3	12
4th	24
5	40
6th	72
7th	126
8th	240
9	272
10	≥ 336
11	≥ 438
12 ^a	≥ 756

Lattice kiss numbers in dimensions 13-24
dimension	Lattice kiss number
13	≥ 918
14th	≥ 1,422
15th	≥ 2,340
16	≥ 4,320
17th	≥ 5,346
18th	≥ 7,398
19th	≥ 10,668
20th	≥ 17,400
21st	≥ 27,720
22nd	≥ 49,896
23	≥ 93,150
24 ^b	196,560

 Die Gitterpackungen für die Dimensionen 12 und 24 haben eigene Namen:

^a Coxeter Todd Grid (after Harold Scott MacDonald Coxeter and John Arthur Todd )

^b Leech grid (after John Leech)

calculation

If the spherical radii are normalized to 1/2 and the origin of the coordinate system is placed in the center of the central sphere, then the following system of inequalities must be fulfilled for N kissing spheres:

{\ displaystyle \ exists}

{\ displaystyle x {\ Big (}}

{\ displaystyle \ forall}

{\ displaystyle n: || x_ {n} || = 1 \ land \ forall n \ neq m: || x_ {n} -x_ {m} || \ geq 1 {\ Big)}}

Here m and n run from 1 to N and is the sequence of the vectors to the N spherical centers, || a || is the norm (length) of the vector a . For reasons of symmetry it is sufficient if the second universal quantifier extends over all m , n with m < n . In a D -dimensional real vector space , this becomes after transition to the standard squares in matrix notation ${\ displaystyle x = (x_ {n}) _ {n \ in \ {1 \ dots {N} \}}}$
${\ displaystyle \ mathbb {R} ^ {D}}$

{\ displaystyle \ exists x {\ Big (} \ forall n: {x_ {n}} ^ {T} x_ {n} = 1 \ land \ forall m <n: (x_ {n} -x_ {m}) ^ {T} (x_ {n} -x_ {m}) \ geq 1 {\ Big)}}

.

The vectors x are understood as column vectors, and x ^T is the corresponding row vector ( transposed matrix ), the scalar product . This system of inequalities is transformed into the system of equations after transformation and the introduction of auxiliary variables ${\ displaystyle a ^ {T} b}$ ${\ displaystyle y_ {mn}}$

{\ displaystyle \ exists x, y: \ sum _ {n = 1} ^ {N} ({x_ {n}} ^ {T} x_ {n} -1) ^ {2} + \ sum _ {\ begin {smallmatrix} (m, n) \ in {N} \ times {N} \\ m <n \ end {smallmatrix}} {\ big (} (x_ {n} -x_ {m}) ^ {T} ( x_ {n} -x_ {m}) - 1- {y_ {mn}} ^ {2} {\ big)} ^ {2} = 0}

.

The above system of equations has a total of equations for the N vectors x , plus half of those for the matrix y ; all in all equations. Because of the relative size of the number N of kissing balls to be tested, the practical limits of predictability are quickly reached. ${\ displaystyle D \ cdot {N}}$ ${\ displaystyle N \ cdot {N} -N}$ ${\ displaystyle D \ cdot {N} + N \ cdot (N-1) / 2}$

Estimates
The general form of the lower bound for -dimensional lattice measures is given by ${\ displaystyle n}$

{\ displaystyle \ eta \ geq {\ frac {\ zeta (n)} {2 ^ {n-1}}}}

,

where is the Riemann zeta function . This limit is specified by the Minkowski-Hlawka theorem (after Hermann Minkowski and Edmund Hlawka ). ${\ displaystyle \ zeta}$

Notes and references

↑ C. Bender: Determination of the greatest number of equal balls that can be placed on a ball of the same radius as the rest. In: Archive Math. Physics. (Grunert) Volume 56, 1874, pp. 302-306.

^ S. Günther: A stereometric problem. In: Archive Math. Physics. Volume 57, 1875, pp. 209-215.

^ R. Hoppe: Comment from the editorial team. In: Archive Math. Physics. (Grunert) Volume 56, 1874, pp. 307-312

↑ Schütte, van der Waerden: The problem of the thirteen balls. In: Math. Annals. Volume 125, 1953, pp. 325-334.

↑ Leech: The Problem of Thirteen Spheres. In: The Mathematical Gazette. Volume 40, 1956, pp. 22-23

^ Oleg R. Musin: The kissing number in four dimensions . In: Annals of Mathematics . Vol. 168, No. 1 , 2008, p. 1-32 , arxiv : math / 0309430 .

^ Andrew M. Odlyzko , Neil JA Sloane : New bounds on the number of unit spheres that can touch a unit sphere in n dimensions. In: J. Combin. Theory. Ser. A, Vol. 26, 1979, No. 2, pp. 210-214

↑ Vladimir I. Levenshtein : О границах для упаковок в n-мерном евклидовом пространстве . No. 6, Docl. Akad. Nauk SSSR 245 1979. pp. 1299-1303

^ Hans D. Mittelmann, Frank Vallentin: High accuracy semidefinite programming bounds for kissing numbers . arxiv : 0902.1105

↑ Follow A001116 in OEIS

↑ ^a ^b https://www.wolframalpha.com/input/?i=kissingnumber Proof from Zinov'ev and Ericson

^ Yves Edel, EM Rains, NJA Sloane: On Kissing Numbers in Dimensions 32 to 128 . In: The Electronic Journal of Combinatorics. Volume 5, Issue 1, 1998

^ John Horton Conway , Neil JA Sloane : The Kissing Number Problem. and Bounds on Kissing Numbers. In: John Horton Conway, Neil JA Sloane: Sphere Packings, Lattices, and Groups. 2nd Edition. Springer-Verlag, New York 1993. pp. 21-24 and 337-339, ISBN 0-387-98585-9 .

^ Neil JA Sloane , Gabriele Nebe : Table of Highest Kissing Numbers Presently Known. http://www.research.att.com/~njas/lattices/kiss.html

↑ Eric W. Weisstein : Coxeter-Todd grid . In: MathWorld (English).

↑ Eric W. Weisstein : Leech grid . In: MathWorld (English).

↑ Sergei Kucherenko et al .: New formulations for the Kissing Number Problem , in: Discrete Applied Mathematics, Volume 155, Issue 14, September 1, 2007, pages 1837–1841, doi: 10.1016 / j.dam 2006.05.012 . The author works with spherical radii standardized to 1.

↑ d. H. an auxiliary matrix , of which only the coefficients with m < n are required. In particular, they can be set to 0, and the matrix can optionally be assumed to be symmetric, antisymmetric or a triangular matrix. ${\ displaystyle y = (y_ {mn}) _ {N \ times {N}}}$ ${\ displaystyle y_ {nn}}$

↑ because of symmetry

↑ Eric W. Weisstein : Minkowski-Hlawka Theorem . In: MathWorld (English).

literature

Florian Pfender , Günter M. Ziegler : Kissing Numbers, Sphere Packings, and Some Unexpected Proofs . Notices of the American Mathematical Society, pp. 873-883. ( PDF )
Eric W. Weisstein : Kissing Number . In: MathWorld (English).
Robert Calderbank: Interview with Neil Sloane (English)
Christine Bachoc, Frank Vallentin: New upper bounds for kissing numbers from semidefinite programming . In: Journal of the American Mathematical Society. Volume 21, 2008, pp. 909-924. arxiv : math.MG/0608426
John Horton Conway, Neil James Alexander Sloane, Eiichi Bannai: Sphere packings, lattices, and groups . Springer, 1999. ISBN 978-0-387-98585-5 . limited online version (Google books)
Casselman on the Kissing Number problem and its history, Notices of the AMS, 2004, Issue 8, PDF file

Web links

Commons : kiss number - collection of pictures, videos and audio files

Wiktionary: kiss number - explanations of meanings, word origins, synonyms, translations

[1] C. Bender: Determination of the greatest number of equal balls that can be placed on a ball of the same radius as the rest. In: Archive Math. Physics. (Grunert) Volume 56, 1874, pp. 302-306.

[2] S. Günther: A stereometric problem. In: Archive Math. Physics. Volume 57, 1875, pp. 209-215.

[3] R. Hoppe: Comment from the editorial team. In: Archive Math. Physics. (Grunert) Volume 56, 1874, pp. 307-312

[4] Schütte, van der Waerden: The problem of the thirteen balls. In: Math. Annals. Volume 125, 1953, pp. 325-334.

[5] Leech: The Problem of Thirteen Spheres. In: The Mathematical Gazette. Volume 40, 1956, pp. 22-23

[6] Oleg R. Musin: The kissing number in four dimensions . In: Annals of Mathematics . Vol. 168, No. 1 , 2008, p. 1-32 , arxiv : math / 0309430 .

[7] Andrew M. Odlyzko , Neil JA Sloane : New bounds on the number of unit spheres that can touch a unit sphere in n dimensions. In: J. Combin. Theory. Ser. A, Vol. 26, 1979, No. 2, pp. 210-214

[8] Vladimir I. Levenshtein : О границах для упаковок в n-мерном евклидовом пространстве . No. 6, Docl. Akad. Nauk SSSR 245 1979. pp. 1299-1303

[9] Hans D. Mittelmann, Frank Vallentin: High accuracy semidefinite programming bounds for kissing numbers . arxiv : 0902.1105

[10] Follow A001116 in OEIS

[wolframalpha-11] ttps://www.wolframalpha.com/input/?i=kissingnumber Proof from Zinov'ev and Ericson

[12] Yves Edel, EM Rains, NJA Sloane: On Kissing Numbers in Dimensions 32 to 128 . In: The Electronic Journal of Combinatorics. Volume 5, Issue 1, 1998

[13] John Horton Conway , Neil JA Sloane : The Kissing Number Problem. and Bounds on Kissing Numbers. In: John Horton Conway, Neil JA Sloane: Sphere Packings, Lattices, and Groups. 2nd Edition. Springer-Verlag, New York 1993. pp. 21-24 and 337-339, ISBN 0-387-98585-9 .

[14] Neil JA Sloane , Gabriele Nebe : Table of Highest Kissing Numbers Presently Known. http://www.research.att.com/~njas/lattices/kiss.html

[15] Eric W. Weisstein : Coxeter-Todd grid . In: MathWorld (English).

[16] Eric W. Weisstein : Leech grid . In: MathWorld (English).

[17] Sergei Kucherenko et al .: New formulations for the Kissing Number Problem , in: Discrete Applied Mathematics, Volume 155, Issue 14, September 1, 2007, pages 1837–1841, doi: 10.1016 / j.dam 2006.05.012 . The author works with spherical radii standardized to 1.