Neutron flux

Physical size
Surname	Neutron flux
Size type	Volume -related product of number and speed
Formula symbol	${\displaystyle \Phi }$
Size and unit system unit dimension SI ${\displaystyle \mathrm {\tfrac {1}{cm^{2}s}} }$ ${\displaystyle L^{-2}T^{-1}}$

Fuel element quarter of a pressurized water reactor, projective representation: The discretization grid on which the calculation is based (bottom), the thermal (middle) and the fast neutron flux with the control rods pulled. It can be seen, among other things, that the neutron flux is location-dependent and within which limits it varies ( see below ).

The neutron flux ( English neutron flux ), and neutron flux density is a physical quantity of nuclear physics , one scalar quantity. It clearly indicates the sum of all distances covered by the free neutrons present in a spatial area in a time interval, divided by the volume of the spatial area and the duration of the time interval. Its usual symbol is (capital phi), its dimension . The usual unit of measurement is cm ⁻² s ⁻¹ , for the sake of clarity it is usually written as n cm ⁻² s ⁻¹ ("neutrons per square centimeter and second"). ${\displaystyle \Phi }$ ${\displaystyle \mathrm {L} ^{-2}\mathrm {T} ^{-1}}$

The neutron flux is neither a flux nor a flux density in the sense of the otherwise usual physical nomenclature.

It can be expressed by the number density of neutrons and the mean value of the velocity values ​​of the neutrons: ${\displaystyle n}$ ${\displaystyle v}$

${\displaystyle \Phi =n\cdot v}$.

The neutron flux can be measured using neutron detectors .

Free neutrons occur in stars , in supernovae and - caused by cosmic rays or thunderstorms - in our natural terrestrial environment. The neutron flux and some related quantities in nuclear reactors , shields , etc. are of particular importance .

definition

The neutron flux in a space is defined as:

${\displaystyle \Phi (t,{\vec {r}}):={\frac {1}{V}}\sum _{i}v_{i}}$

Here are:

• ${\displaystyle i}$: the counting variable for the neutrons (for a possible selection of the counted neutrons see "Neutron angle density and other differential quantities")
• ${\displaystyle t}$: the time at which the number of neutrons and their speed is recorded,
• ${\displaystyle {\vec {r}}}$: the position vector indicating the position of the spatial area,
• ${\displaystyle V}$: the volume of the considered spatial area,
• ${\displaystyle v_{i}}$: the magnitude of the velocity of the -th neutron. ${\displaystyle {\vec {v}}_{i}}$ ${\displaystyle i}$

Independent variable

The neutron flux depends not only on the location but also on the kinetic energy of the neutrons and can change over time : ${\displaystyle E}$ ${\displaystyle t}$

${\displaystyle \Phi =\Phi ({\vec {r}},E,t)}$.

The vector is the position vector which specifies the position of a spatial area - in the limiting case infinitesimally small - in a three-dimensional coordinate system . Consequently, the neutron flux generally depends on five independent variables. ${\displaystyle {\vec {r}}}$

Clear explanation

The neutron flux in the point in space can also be illustrated by the idea of ​​a small circular disk with the center , which is penetrated by the neutrons. One imagines that the circular disk is rotated in space with a fixed center for each individual neutron so that the neutron falls in the direction of the normal . The neutron flux is then the number of neutrons that penetrate the disk in a time interval, divided by the time interval and by the area of ​​the disk. Turning the disk in all directions produces a sphere with the diameter of the disk as the envelope. ${\displaystyle {\vec {r}}}$ ${\displaystyle {\vec {r}}}$

Neutron angle density and other differential quantities

The selection of the neutrons to be counted at the time in the volume around the location can be made according to whether the neutrons have an energy within an energy range and at the same time their flight direction lies in the vicinity of a given flight direction with the unit vector ( ). This results in the differential quantity neutron angle density ( English angular neutron density ) or angle density for short : ${\displaystyle t}$ ${\displaystyle V}$ ${\displaystyle {\vec {r}}}$ ${\displaystyle E_{i}}$ ${\displaystyle E-\delta E\leq E_{i}\leq E+\delta E}$ ${\displaystyle {\hat {e}}_{i}}$ ${\displaystyle {\vec {\Omega }}}$ ${\displaystyle {\hat {e}}_{i}\cdot {\vec {\Omega }}\geq 1-\delta e}$ ${\displaystyle n}$

${\displaystyle n({\vec {r}},E,t,{\vec {\Omega }}):=\lim _{V\rightarrow 0}\lim _{\delta E\rightarrow 0}\lim _{\delta e\rightarrow 0}{\frac {1}{V}}{\frac {1}{\delta E}}{\frac {1}{4\pi (\delta e)^{2}}}\Phi (t,{\vec {r}},V,E,\delta E,{\vec {\Omega }},\delta e)}$.

A precise analysis of the transport processes of neutrons in a nuclear reactor (correspondingly also of other particles) requires the definition of further parameters linked to the neutron flux. The names of these quantities are not the same in all reactor physics textbooks. Here we follow the naming and definition of some of these quantities according to the textbook Nuclear reactor theory by Bell and Glasstone.

Neutron flux spectrum

The quantity neutron flux spectrum , neutron spectrum , neutron energy spectrum , energy-differential neutron flux or energy-dependent neutron flux is the partial derivative of the neutron flux according to the energy:

${\displaystyle \varphi ({\vec {r}},E,t)={\frac {\partial \Phi ({\vec {r}},E,t)}{\partial E}}}$.

The unit of measurement is accordingly z. B. n cm ⁻² s ⁻¹ eV ⁻¹ , neutrons per square centimer, second and electron volts. The flow of neutrons with energies between and is . ${\displaystyle E}$ ${\displaystyle E+\partial E}$ ${\displaystyle \varphi (E)\,\partial E}$

Direction of flight of the neutrons

The unit vector of the neutron flight direction and its components, the polar angle and the azimuth angle in spherical coordinates ${\displaystyle {\vec {\Omega }}}$ ${\displaystyle \theta }$ ${\displaystyle \varphi }$

To distinguish neutrons according to their direction of flight, two further independent variables are required, which are combined in the vector neutron flight direction (unit vector of the neutron flight direction ).

The following should be added: There are quantities in physics that depend on the location and the momentum, for example the wave function of quantum mechanics . In addition to the position coordinates , the impulse components are also included in the symbols as independent variables for such quantities . If such a quantity is also dependent on time , then one symbolizes the dependence of the quantity on seven independent variables . ${\displaystyle {\vec {r}}=(x,y,z)}$ ${\displaystyle {\vec {p}}=(p_{x},p_{y},p_{z})}$ ${\displaystyle f}$ ${\displaystyle t}$ ${\displaystyle f}$ ${\displaystyle f({\vec {r}},{\vec {p}},t)}$

In reactor physics , one could also calculate with these seven independent variables, the three position coordinates, the three momentum components and the time. But instead of the three momentum components one chooses three other independent variables, the kinetic energy of the neutrons and two solid-angle variables that record the direction of flight of the neutrons. They are the polar angle and the azimuth angle of the flight direction (normalized to the value 1) in spherical coordinates , as shown in the figure. ${\displaystyle E}$ ${\displaystyle {\vec {\Omega }}=(\theta ,\varphi )}$ ${\displaystyle \theta }$ ${\displaystyle \varphi }$

The vector , the unit vector in the direction of neutron motion, is defined by ${\displaystyle {\vec {\Omega }}}$

${\displaystyle {\vec {\Omega }}={\frac {{\vec {v}}(E)}{|{\vec {v}}(E)|}}={\frac {{\vec {v}}(E)}{v(E)}}}$.

The speed vector and the amount of the speed vector symbolize , each depending on the kinetic energy . ${\displaystyle {\vec {v}}(E)}$ ${\displaystyle |{\vec {v}}(E)|}$ ${\displaystyle v(E)}$ ${\displaystyle E}$

Note the difference between this two-component vector and the usual solid angle , which is a scalar and is symbolized with, which can lead to misinterpretations. ${\displaystyle {\vec {\Omega }}}$ ${\displaystyle \Omega }$

With these independent variables to a reactor physical quantity symbolized then with appropriately . This choice of the independent variables has proven to be expedient and, from a physical point of view, is equivalent to a choice of the impulse components. The momentum components can be calculated from the kinetic energy and the solid angle vector and vice versa. ${\displaystyle f}$ ${\displaystyle f({\vec {r}},E,{\vec {\Omega }},t)}$

Neutron angular flux

The neutron flux angle ( Angular neutron flux ) or short angle River is the dependent variable of the neutron transport equation ( neutron transport equation ) and thus one of the most important physical parameters of the reactor theory at all. It is defined as

${\displaystyle \psi ({\vec {r}},E,{\vec {\Omega }},t)=v\cdot n({\vec {r}},E,{\vec {\Omega }},t)}$.

Neutron Flux or Neutron Scalar Flux

From the neutron angular flux, the neutron flux defined above results simply as the integral of the angular flux over all spatial directions:

${\displaystyle \Phi ({\vec {r}},E,t)=\int _{4\pi }d{\vec {\Omega }}\psi ({\vec {r}},E,{\vec {\Omega }},t)}$.

Because the neutron flux is formed by integration via the vector quantity neutron angular flux , the neutron flux in the context of neutron transport theory is also referred to as neutron scalar flux or scalar neutron flux .

Neutron fluence

By integrating the neutron flux or the neutron flux spectrum over time, e.g. B. the duration of an irradiation, the total or energy-dependent neutron fluence results . It is important to calculate z. B. caused by neutron radiation damage or the yield of a neutron activation .

Importance for nuclear reactors

In connection with nuclear reactors, the parameter neutron flux is mainly used to answer the question of whether and why a fissile material arrangement (nuclear reactor) becomes critical , and to calculate nuclear reaction rates in the reactor. Without knowledge of spatially and energetically sufficiently "resolved" nuclear reaction rates, both questions cannot be answered. The decisive parameter of the nuclear reaction rate density is the product of the neutron flux and the material-dependent size of the macroscopic cross-section . The macroscopic cross-section depends on the particle densities and nuclear properties of all nuclides with which the neutrons “share” the spatial area.

In a nuclear reactor, the neutron flux is generally dependent on location, neutron energy and time. In a consistently critical held reactor can neglect the time dependence over a small period of time. One then speaks of the stationary state of the reactor. The total or thermal neutron flux is relatively easy to measure, e.g. As with the reactor core built fission chambers .

The power density in a volume area of ​​the reactor results from the product of the neutron flux and a special cross-section, a material and location-dependent variable . If one assumes (in a somewhat simplistic way) that the shape of the spatial distribution of the neutron flux over the reactor core always remains the same, then measuring the neutron flux at one point is sufficient to infer the total output of the reactor. A temperature measurement, on the other hand, would not be suitable as a measure of performance, because the temperature at one point is the result of the performance at the point itself, the performance in neighboring areas in the recent and medium past, and the cooling performance.

The flow measurement signal is therefore generally used to control and monitor the reactor. Even when the (subcritical) reactor is switched off, the flow measurement is kept in operation. A radioactive neutron source built in for this purpose always ensures a low neutron flux; this means that the function of the measuring instrumentation is continuously monitored.

Mean and discretization

A measured neutron flux value is always an average value over a certain spatial area, an energy interval and a period of time. A discretization of the independent variables is also necessary for calculations of the neutron flux , since the corresponding equations can only be solved numerically. The interval sizes for the discretization are usually determined before this calculation.

Spatial discretization

The size and shape of the area of interest can vary greatly. In the case of an extensive arrangement, such as a reactor core, the available computing capacity sets practical limits for the resolution in small spatial areas. How finely the spatial resolution must be chosen depends on the mean free path of the neutrons; this is determined by the neutron energy and the respective medium. Typical dimensions of the individual “cells” in reactor calculations are in the centimeter range.

Energy discretization

Neutron flux spectrum of the fuel element of a pressurized water reactor in a double logarithmic representation. The discretization grid on which the calculation is based is shown as a miniature image at the top right.

The energy resolution is selected in reactor calculations depending on the issue, from the total range of possible neutron energy (10 ⁻⁴ to 2 · 10 ⁷ ) eV - i.e. no “resolution” at all - up to a few hundred energy intervals (“neutron groups”). In the case of thermal reactors, for some questions it is sufficient to divide them into two groups ( thermal flow and fast flow ; see first figure). For fast reactors , calculations are e.g. B. often carried out with 26 groups.

By integrating the neutron flux spectrum over the energy interval of the respective neutron group, the so-called group fluxes are calculated. For example, in the case of two energy groups, these are the integrals

${\displaystyle \Phi _{\text{thermisch}}=\int _{E_{u}}^{E_{1}}\varphi ({\vec {r}},E,t)\ \mathrm {d} E}$ (thermal flow) and

${\displaystyle \Phi _{\text{schnell}}=\int _{E_{1}}^{E_{o}}\varphi ({\vec {r}},E,t)\ \mathrm {d} E}$ (fast flow).

In the example in the first figure, the energy limits , and were used. ${\displaystyle E_{u}=10^{-4}\ \mathrm {eV} }$ ${\displaystyle E_{1}=0{,}625\ \mathrm {eV} }$ ${\displaystyle E_{o}=20\ \mathrm {MeV} }$

The neutron flux spectrum is u. a. required as a weighting function in order to obtain the so-called group constants for neutron diffusion calculations .

The figure shows the neutron flux spectrum of a fresh fuel element of a pressurized water reactor (PWR). It is the same model to which the neutron flux distributions shown at the beginning of the article belong and was also calculated with the HELIOS 1.8 program system. The figure shows the neutron flux spectrum of a selected coolant region ( region 1 , the region at the top left corner) and the mean value of the neutron flux spectrum, averaged over the entire fuel assembly. One recognises:

• The energy at the maximum of the neutron flux spectrum is close to the thermal energy of 0.0253 eV (20 ° C).
• The neutron flux spectrum breaks off at around 20 MeV, since nuclear fission does not produce neutrons with a higher energy.

Example: neutron flux in a pressurized water reactor

Cross-sections through calculation cells of the pressurized water reactor under consideration: cell with fuel rod and cell with control rod guide tube. Scheme of the cell on the left, the discretized cell on the right

Cross-section through a quarter of a fuel element of the pressurized water reactor under consideration

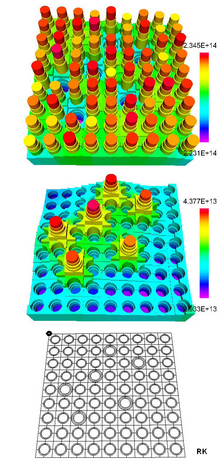
The first figure of the article shows the horizontal position dependence of the thermal and the fast neutron flux over the cross section of a fuel element of a pressurized water reactor in a stationary state, obtained from a neutron transport calculation with the cell and combustion program HELIOS 1.8 and cross sections from the core data library ENDF / B-VI data files (Rose and Dunford, 1990).

The fuel assembly grid contains two types of "cells": fuel rod cells and guide tube cells. The fuel rod cell contains three materials: fuel (red), zircalloy shell (green) and water (blue), the guide tube cell only the guide tube and water. The adjacent figure shows the two cell types on the left and their discretization in 6 or 8 regions on the right.

The fuel assembly is an 18 × 18 arrangement with 300 fuel rods and 24 control rod guide tubes into which neutron absorbers can immerse. The control rods are drawn into this calculation. Since the fuel assembly is symmetrical, it was enough to calculate a quarter of the fuel assembly shown in the graph. The center of symmetry (the center of the fuel assembly cross-section) is marked on the discretization grid at the top left as a small black square.

The thermal flow is greatly increased at the locations of the drawn control rods, which can be clearly seen in the middle part of the first illustration of the article by the six red to orange colored maxima. The fast flow, however, is comparatively low in these places. The numbers in the figure indicate the flow values ​​in n cm ⁻² s ⁻¹ at a specific heat output of 37.4 W / g heavy metal . In this model case, the fast flow lies in the interval (2.2 · 10 ¹⁴ - 2.3 · 10 ¹⁴ ) neutrons cm ⁻² s ⁻¹ , the thermal flow in the interval (2.9 · 10 ¹³ - 4.4 · 10 ¹³ ) Neutrons cm ⁻² s ⁻¹ .

Nuclear reactors

The neutron flux values ​​(more precisely: neutron angular flux values ) in a nuclear reactor obey the neutron transport equation , a balance equation for neutrons. Solving this integro-differential equation numerically is one of the most demanding tasks in physics and numerical mathematics .

Program systems for the numerical solution of the neutron transport equation, for example for a nuclear reactor fuel element in a spatial and energetic resolution, as shown in the figure at the beginning of the article, are developed by very few specialized companies in the world. They are either state-dominated companies, for example in France under the umbrella of EDF or the CEA ( APOLLO program system ), or companies under private law such as Studsvik Scandpower ( CASMO and HELIOS program systems ). The private law firms mostly emerged through the outsourcing of working groups that began with the program development in a state institute or at a university. The development of such program systems takes tens of person-years and is currently not possible at a university. In addition, every developer has to familiarize himself with the physical theory and the mathematical-numerical solution methods of several years before he can even start programming. A user of such a program should also allow about three to five years for training.

A whole chain of programs is required for the development of new types of nuclear reactors, for example a molten salt reactor for power operation or for the routine operation of an existing nuclear power plant. a. also far less “complex” neutron transport programs that solve special tasks numerically. However, the first link in this chain always remains a high-performance neutron transport program. The common type name cell and burn-off program for such a program only suggests its scope of services. These cell and burn programs were (as of 2007) written exclusively in Fortran of different versions. A program system of this type cost at least $ 100,000 in 2000.

However, the behavior of the neutrons in the reactor can also be roughly described as a diffusion process. Such a neutron diffusion program only calculates the neutron flux, not the neutron angular flux. Roughly speaking, a program of this type can be developed in two to five person-years (depending on the spatial dimension: 1D, 2D, 3D). The common programming language for a neutron diffusion program is also Fortran. Programs of this type are provided free of charge for public institutes and universities from the database of the NEA Computer Program Library , especially under the category C. STATIC DESIGN STUDIES (training period several months).

Monte-Carlo computer programs such as MCNP (“Monte-Carlo N-Particle Transport Code”) are also used for special tasks .

Fusion reactors

The Monte Carlo method is generally used to calculate the neutron flux distribution and the related variables in fusion reactors and corresponding test facilities.

Natural neutron flux

Neutron-induced nuclear reactions in AGB stars ( english asymptotic giant branch ) are responsible for most of the natural elements through nucleosynthesis have emerged. These are elements more massive than iron. The neutron flux is relatively low and is of the order of 10 ⁵ to 10 ¹¹ n cm ⁻² s ⁻¹ . It leads to nucleosynthesis through the s-process ( English slow neutron capture process ).

In contrast to this, the neutron flux after the explosion of a massive star ( supernova ) is very high and reaches the order of magnitude of 10 ³² n cm ⁻² s ⁻¹ . This leads to nucleosynthesis through the r-process ( English Rapid Neutron Capture Process ).

In the earth's atmosphere, cosmic radiation , which mainly consists of high-energy protons (1 GeV and higher), generates free neutrons by spallating the atomic nuclei of nitrogen and oxygen. At the same time, it generates secondary protons and charged and neutral pions , which in turn can release neutrons in further reactions. The resulting neutron flux strongly depends on the primary proton flux and the location of the reaction in the atmosphere.

In the case of lightning , atoms of atmospheric nitrogen and oxygen are ionized, but also the heavy water that is always present in a cloud of water vapor . In the electric field of the lightning discharge, the ions (like the released electrons) can be accelerated and trigger nuclear reactions, which in turn release neutrons. In particular, fusion reactions can also occur. For these processes, theory and experiment are still at the beginning. The atmospheric neutron flux during a thunderstorm reaches up to about 90 n cm ⁻² s ⁻¹ .

Further numerical examples for the neutron flux

The “Research with Neutrons Committee” distinguishes between research neutron sources (FNQ)

• Spallation sources. There are 2 spallation neutron sources in Europe.
• Reactors with high neutron flux ( > 10 ¹⁵ n cm ⁻² s ⁻¹ ). There is such a high flux reactor in Europe, in the ILL . ${\displaystyle \Phi _{\mathrm {th} }}$
• Reactors with a medium neutron flux (10 ¹⁴ n cm ^-2 s ^-1 < <10 ¹⁵ n cm ^-2 s ^-1 ). There are 3 such FNQs in Europe. ${\displaystyle \Phi _{\mathrm {th} }}$
• Reactors with low neutron flux ( ≤ 10 ¹⁴ n cm ⁻² s ⁻¹ ). There are 7 such FNQs in Europe. ${\displaystyle \Phi _{\mathrm {th} }}$

${\displaystyle \Phi _{\mathrm {th} }}$ means the thermal neutron flux.

The spallation neutron source SINQ achieves a total neutron flux of 10 ¹⁴ n cm ⁻² s ⁻¹ , the research reactor FRM-II 8 × 10 ¹⁴ n cm ⁻² s ⁻¹ .

In a fusion reactor , the wall of the plasma vessel will also be exposed to a neutron flux of around 10 ¹⁴ n cm ⁻² s ⁻¹ , which here consists predominantly of neutrons with a high energy of around 14 MeV.

Web links

• C. STATIC DESIGN STUDIES
• NEA Computer Program Library

Individual evidence

1. ↑ Dieter Emendörfer, Karl-Heinz Höcker: Theory of nuclear reactors . Bibliographical Institute, Mannheim / Vienna / Zurich 1970 (380 pages).
2. ^ Dieter Smidt: Reactor technology . 2nd Edition. Braun, Karlsruhe 1976, ISBN 3-7650-2019-2 (XVI, 325 pages). On p. 20, Smidt gives almost literally the same definition for neutron flux as Emendörfer / Höcker, Theory of Nuclear Reactors Vol. 1 on p. 63 for neutron flux density, namely: "The total distance covered by all neutrons of a volume unit in a unit of time."
3. ^ Albert Ziegler: Textbook of reactor technology . Springer, Berlin / Heidelberg 1983, ISBN 3-540-12198-6 (XI, 242 pages).
4. ↑ Albert Ziegler, Hans-Josef Allelein (ed.): Reactor technology: physical-technical basics . 2nd, revised edition. Springer Vieweg, Berlin 2013, ISBN 978-3-642-33846-5 (634 pages, limited preview in the Google Book Search [accessed on January 21, 2018]).
5. ^ ^{A b c d} Samuel Glasstone, Milton C. Edlund: The elements of nuclear reactor theory . MacMillan, London 1952 (VII, 416 pp.). This monograph occupies a prominent position because like no other it shaped the then young generation of reactor physicists in West and East and the later textbook writers. It is fully online in the 6th print from February 1957. babel.hathitrust.org . Full text search is possible.
6. ^ ^{A b} James J. Duderstadt, Louis J. Hamilton: Nuclear reactor analysis . Wiley, New York 1976, ISBN 978-0-471-22363-4 (xvii, 650 pages). The authors write on p. 106: "... the tradition in nuclear engineering of referring to this quantity as the neutron" flux "is very misleading." (... the tradition in nuclear engineering to designate this quantity as the neutron "flux" is very misleading.)
7. ↑ As far as the monographs cited here are concerned, Duderstadt and Hamilton (p. 106) are the only authors who explicitly address the fallacy of the name neutron flux . Other English-speaking authors do this implicitly, e.g. B. Weinberg and Wigner s. o., by the name of track length ( track length bring) into play. This name is also far removed from the usual naming for physical quantities . He suggests that this size has the dimension of a length. The fact that some authors correctly add that this orbit length still has to be divided by the volume of the spatial area and the time interval in which the orbit length was "measured" does not change this . The authors of German-language monographs (at least those cited here) define and interpret the names neutron flux and orbit length uncritically. Some authors even "dilute" their definitions, for example by using units of measurement : "This (the neutron flux density) can be understood as the total orbit length covered by all neutrons per cm ³ and s." (Ziegler 1983, p. 58)
8. ^ Alvin M. Weinberg, Eugene Paul Wigner: The physical theory of neutron chain reactors . Univ. of Chicago Press, Chicago 1958, ISBN 0-226-88517-8 (XII, 800 pages). The authors write on p. 23: “The quantity nv (ie, the flux of incident particles) has the dimension of cm ⁻² sec ⁻¹ . It is sometimes also called "track length," since it is the total distance traveled during unit time by all particles contained in unit volume. " (The size nv (i.e. the flow of the incident particles) has the dimension cm ⁻² sec ⁻¹ . It is sometimes also called "orbit length", since it is the total distance that during the unit of time of all particles contained in the unit of volume is covered.)
9. ↑ ^{a b c} Karl Wirtz , Karl Heinz Beckurts : Elementare Neutronenphysik . Springer, Berlin 1958 (VIII, 243 pp., Limited preview in the Google book search [accessed on January 3, 2018]).
10. ↑ Aleksey D. Galanin: Theory of thermal nuclear reactors . Teubner, Leipzig 1959 (XII, 382 pages). The original monograph was published in Russian that same year and a year later by Pergamon Press in English under the title “Thermal reactor theory”.
11. ↑ Rudi JJ Stamm'ler, Máximo J. Abbate: Methods of steady-state reactor physics in nuclear design . Acad. Press, London 1983, ISBN 0-12-663320-7 (XVI, 506 pages).
12. ^ Paul Reuss: Neutron physics . EDP ​​Sciences, Les Ulis 2008, ISBN 978-2-7598-0041-4 (xxvi, 669, limited preview in Google book search). On p. 98 of this monograph, the parameters neutron density, neutron flux and nuclear reaction rate are very clearly defined.
13. ^ KH Beckurts, K. Wirtz: Neutron Physics. Springer 1964, ISBN 978-3-642-87616-5 , pages 82-83
14. ↑ A. Ziegler, HJ Allelein (Ed.): Reaktortechnik . Physical and technical basics. 2nd Edition. Springer 2013, ISBN 978-3-642-33845-8 , page 58
15. ↑ George I. Bell, Samuel Glasstone: Nuclear reactor theory . Van Nostrand Reinhold, New York 1970, p. 2 ff . (XVIII, 619 pp.).
16. ↑ "Neutron spectrum" is ambiguous. It could also be the neutron number density spectrum.
17. ↑ In the case of the calculation model shown in the figure, the "centimeter range" was sometimes undercut.
18. ↑ H. Giese: KfK Analysis of the Superphenix-1 control rod experiments part 2: Rod worth calculations. Nuclear Research Center Karlsruhe Report KfK-4896 (1992)
19. ↑ For reactor calculations with only two groups, the limit energy of 0.625 eV is a "quasi-standard".
20. ↑ ^{a b c} Rudi JJ Stamm'ler et al .: HELIOS Methods: Version 1.8 . Studsvik Scandpower 2003 (192 pages).
21. ↑ ^{a b} RK: PWR-Calculations with the Code-System HELIOS 1.8 , Studsvik 2005 International User's Group Meeting, Charlotte, NC, USA, June 1-3, 2005.
22. ↑ www-nds.iaea.org
23. ↑ To a good approximation, the neutron flux is proportional to the specific heat output . The specific heat output of the reactor is the quotient of the total heat output and the initially used heavy metal mass of the reactor core. The reactor of the Emsland nuclear power plant, for example, is operated with a thermal output of 3850 MW. The heavy metal mass initially used is 103 t. This results in an average specific power of 37.4 W / g.
24. ↑ Studsvik studsvik.episerverhosting.com in the case of the CASMO program system , University of Oslo in the case of the HELIOS program system . Both companies merged in the early 2000s to form Studsvik ScandPower
25. ↑ When developing a new type of reactor, the proportion of what can be summarized under neutron physics requires only approx. 20% of the total effort.
26. ^ RA Forster, LJ Cox, RF Barrett et al .: MCNP Version 5. Nuclear Instruments in Physics Research Section B Volume 213 (2004) pages 82-86
27. ↑ Z. Xu, J. Rhodes, K. Smith: CASMO-5 versus MCNP-5 benchmark of radial power profile in a fuel pin. Int. Conf. on Mathematics, Computational Methods and Reactor Physics , Saratoga Springs, 2009 (PDF)
28. ^ Y. Li, L. Lu, A. Ding, H. Hu, Q. Zheng, S. Zheng, Y. Wu: Benchmarking of MCAM 4.0 with the ITER 3D model. Fusion Engineering and Design Volume 82 (2007) pages 2861-2866
29. ↑ SP Simakov, U. Fischer, K. Kondo and P.Pereslavtsev: Status of the McDeLicious Approach for the D-Li neutron source term modeling in IFMIF Neutronics Calculations. Fusion Science and Technology Volume 62 (2012) pages 233-239
30. ↑ P. Pereslavtsev, L. Lu, U. Fischer, O. Bitz: Neutronic analyzes of the HCPB DEMO reactor using a consistent integral approach. Fusion Engineering and Design Volume 89 (2014) pages 1979-1983
31. ^ E. Margaret Burbidge, GR Burbidge, William Fowler, Fred Hoyle: Synthesis of the Elements in Stars . In: Rev. Mod. Phys. tape 29 , no. 4 , 1957, pp. 548-650 , doi : 10.1103 / RevModPhys.29.547 .
32. ^ Neutrons Born In Lightning . PhysOrg, 2005
33. ↑ Christoph Köhn, Ute Ebert: Calculation of beams of positrons, neutrons and protons associated with terrestrial gamma-ray flashes . In: Journal of Geophysical Research: Atmospheres , 2015, 120, pp. 1620–1635. doi: 10.1002 / 2014JD022229
34. ↑ AV Gurevich , AM Almenova: Observations of high-energy radiation during thunderstorms at Tien-Shan . In: Physical Review D . Americal Physical Society, 2016, 94 (2), p. 023003. doi: 10.1103 / PhysRevD.94.023003
35. ↑ Christoph Köhn, Gabriel Diniz, Mushin N. Harakeh: Production mechanisms of leptons, photons, and hadrons and their possible feedback close to lightning leaders . In: Journal of Geophysical Research: Atmospheres , 2017, 122, pp. 1365-1383, doi: 10.1002 / 2016JD025445
36. ↑ sni-portal.de
37. ^ Research neutron source Heinz Maier-Leibnitz
38. ^ Weston M. Stacey: Fusion. An Introduction to the Physics and Technology of Magnetic Confinement Fusion. Wiley-VCH, 2010, ISBN 978-3-527-40967-9 , limited preview in Google Book Search