Level-k reasoning

The level-k argument ( english level-k reasoning ) is a model of the economic parts of the behavioral economics and game theory , which attempts the human decision-making in strategic games to explain. In experiments, a significant deviation of the players from the predicted behavior from the standard theories, such as backward induction or the iterative elimination of strictly dominated strategies , is sometimes observed. The level-k reasoning was first introduced by Rosemarie Nagel and Dale O. Stahl and Paul W. Wilson and is an attempt to improve the accuracy of such predictions.

Theoretical model

Most behavioral theories assume that players are thinking strategically , which means that they make guesses about the likely actions of other players and find best answers based on those guesses . However, this rationality alone is not enough to make an accurate prediction about the outcome of the game, since players can be wrong when forming their guesses.

Accordingly, behavioral economists also assume that each player's guess about the behavior of the other players corresponds to their actual behavior. The assumption of mutual rationality and the assumption of mutual consistency thus jointly define the equilibrium .

However, many games, both real and fictional, result in game outcomes that deviate from the predicted equilibria of standard theories. To explain these deviations, Rosemarie Nagel, among others , developed the non-equilibrium model of the level-k argument based on the beauty contest according to John Maynard Keynes , as well as Stahl and Wilson, based on 12 different, symmetrical 3x3 games . According to this theory, the players can be categorized according to the level of their strategic considerations and thus the assumption of limited rationality is in focus.

Rosemarie Nagel's model

The crucial difference between the level-k argument and equilibrium models is that it allows for heterogeneity in the decision-making of the players. This is captured by the levels of strategic considerations . The level-k reasoning specifies the behavior of these types of players as follows. ${\ displaystyle \ textstyle k = 0,1,2,3, ...}$

Level 0 players are non-strategic . This means that you can make assumptions about the likely actions of the other players, but do not take them into account during the decision-making process, so you are not looking for the best answer to these. Nagel assumes here that the actions of the level 0 players are evenly distributed over all possible actions. Types of players at higher levels (i.e., ) make guesses about the distribution of the lower types of players and use these to choose a best answer as their action. ${\ displaystyle \ textstyle k \ geq 1}$

In Nagel's original model, the players assume that all other players belong to the next lower player type. So a level 1 player assumes that all other level 0 players are and forms his best answer accordingly. A level 2 player therefore assumes that all other level 1 players are. This pattern of behavior continues for higher types of players, with each player having a finite number of trains of thought . This means that individuals are limited in how deeply they can think strategically.

An important implication of the level-k reasoning in its original form is the assumption that each player is at the highest level of all the players in the game. At some level-k, players will neglect the fact that other players might be level-k or even higher as well. This behavior has been attributed to many factors, such as maintenance costs or simply overconfidence .

Stahl and Wilson's model

In Stahl and Wilson's version, players do not determine their best answer without errors. As in Nagel's model, an even distribution of the actions of the level 0 players across all possible actions is assumed, but this is viewed as imprecise. The errors manifest themselves in the fact that level-1 and level-2 players find the best answers, whereby actions with a higher payout are chosen with a higher probability.

Higher level player types are not considered in this form of level-k argument . In addition to the classic level-k player types, Stahl and Wilson introduce other types. The naive Nash player chooses the Nash equilibrium , the secular player finds a best answer on the distribution of the level-k players and the naive Nash player, and the rational expectations player finds a best answer based on correct guess about the frequency of everyone else Types. With the exception of the latter, the other two types of players can also be represented in Nagel's model.

The Classic Game: Beauty Contest

Probably the most frequently studied example of the deviant behavior of the players in experiments in connection with the level-k reasoning is the beauty contest according to John Maynard Keynes . Rosemarie Nagel described the game as follows: Suppose there are many players, each of whom simultaneously selects an integer from the range of numbers . The winner is the player whose chosen number is closest to the mean of all chosen numbers (multiplied by a generally known parameter , whereby usually ). If two or more players are equidistant from this number, the payout will be split evenly between the winners (or randomly decided who won). ${\ displaystyle \ textstyle [0.100]}$ ${\ displaystyle \ textstyle p}$ ${\ displaystyle \ textstyle 0 \ leq p <1}$

Nash equilibrium through iterative elimination of strictly dominated strategies

The standard solution for the Keynes beauty pageant is determined by iterative elimination of strictly dominated strategies . Be for all subsequent considerations of the beauty pageant. ${\ displaystyle \ textstyle p = {\ frac {2} {3}}}$

A completely rational player will observe that the highest possible mean multiplied by 67 is. This player will also predict that the other players also know this and will act accordingly so that the maximum possible number becomes 45. The other players should know that too. This process repeats itself indefinitely and ends with all players choosing 0, the Nash equilibrium , for this game. If only whole numbers are allowed, there is also the Nash equilibrium, in which all players select 1. ${\ displaystyle \ textstyle p}$

Level-k reasoning in the beauty pageant

However, in experiments it is observed that most players choose numbers around either 22 or 33. This can be explained with the help of the level-k argument : A level-1 player assumes that all other level-0 players are, i.e. a number is non-strategic (e.g. random number, number with a special meaning for the player) choose. In Nagel's model, these random numbers are evenly distributed over all possible numbers, so the mean is 50. A level-1 player chooses 33 as the best answer. A level-2 player in turn assumes that all other players are level-1 and chooses 22 as the best answer. This process is repeated accordingly for players of higher levels.

The observed deviations from the Nash equilibrium agree with the player types of the first and second level and support the level-k argument . Only a small proportion of players have deeper thoughts than those of level 2.

Limitations of level-k reasoning

Level 0 players

The distribution of level-0 players within the population is an essential part of the level-k argument , as it forms the basis for the decisions of all types of players at a higher level. The prevailing opinion in the literature is that this basic type of player is just a construct in the minds of higher-level players. Not only is level 0 behavior difficult to prove empirically, but there are even studies that show with a general discrete distribution that the estimated proportion of such player types is often 0.

In general, both the original versions of the level-k reasoning according to Nagel, Stahl and Wilson and most of the later extensions and models assume that level-0 players choose their action randomly from all possible actions and thus evenly across all possible actions are distributed. An alternative assumption of level 0 behavior is that such types of players choose the most prominent choice among all possible actions.

This shows that level 0 players are not only existential for determining the higher levels of strategic considerations, but also always require certain assumptions. Accordingly, depending on the context, game format and / or research question, a different level 0 behavior is assumed. Which specification is best is sometimes seen as an empirical challenge.

Categorization of the types of players

In the context of the level-k argumentation , the problem of the pure observation data also represents a major challenge for economists. It is not uncommon for the behavior of the players to be used alone to derive the actually underlying decision rule. As a result, behavioral theorists are increasingly trying to develop methods with which additional information about the decision-making processes of the players can be obtained.

Typically, economists collect data for a particular game and then find a suitable distribution of player types within the population. Such ex post distributions may not provide any information as to whether a decision can be traced back to a certain level of strategic considerations or some other underlying decision rule.

Different approaches to improved categorization of player types

A large number of alternative approaches were pursued to improve the categorization of player types. One approach identifies an individual's decision rule by examining their behavior patterns in a variety of games in the same class and assigning them the type of player that best fits their overall behavior.

Another approach confronts the observed actions with additional data that provide clues about the decision-making process to determine the types of players. For example, some researchers examined information-seeking data recorded with MouseLab, others used ex-post participant explanations of their decisions, and still others analyzed players' arguments to persuade their teammates to follow their advice.

11-20 Money Request Game

As a contrast to these earlier approaches in the literature developed Ayala Arad and Ariel Rubinstein , the 11-20 money request game (English 11-20 Request Money Game ). In the basic version, two players are asked to individually request a whole number between 11 and 20 shekels . After that, each player receives the amount they asked for. If a player demands exactly one shekel less than the opponent, he receives an additional 20 shekels.

This relatively simple game format enables an instinctive, clear specification of the player types according to the level-k argument . Furthermore, determining the best answers is both simple and accurate: level-0 players choose the prominent 20, and level-1 (-2) players answer best with 19 (18).

An experiment with students from Tel Aviv University gave clear indications that the Nash equilibrium could not explain the behavior observed: more than two-thirds of the players asked for 17, 18 or 19 shekels. The written explanations suggest that choices below 17 shekels are more a result of random decisions than strategic considerations.

Extensions to level-k reasoning

After the introduction of the level-k argumentation by Nagel and Stahl and Wilson, various economists examined various games in the most diverse of variations. Due to the previously described limitations of the theory, a large number of extensions and modeling of the original model were made.

For example, there are some theorists who note that a player does not necessarily have to fall into one of the above types of players. Instead, assuming that a certain percentage of each type of player is represented in the population, a player could find his corresponding best answer.

Theory of the cognitive hierarchy (cognitive hierarchy theory)

The theory of the cognitive hierarchy (English Cognitive Hierarchy Theory , CHT ) goes back to Colin Camerer , Teck-Hua Ho and Juin-Kuan Chong . The main difference to the level-k argument lies in the distribution of the different types of players within the population .

In particular, Camerer, Ho and Chong assume in their model that the players do not assume that all other players belong exactly to the next lower level, but that all lower types of players are represented to a certain extent in the population. Furthermore, the CHT assumes that all players make correct guesses about the relative frequency of these lower types of players and that this true distribution follows a Poisson distribution with parameters . ${\ displaystyle \ textstyle \ tau}$

In the example of the beauty pageant, the level-1 players continue to assume that all other players are level-0 players and choose 33. However, level-2 players now suspect that both types of players exist in the population - the exact ratio depends on the true one Distribution within the population, that is , from. Accordingly, they will choose a number greater than 22. ${\ displaystyle \ textstyle \ tau}$

Generalized Cognitive Hierarchy Theory

The generalized theory of the cognitive hierarchy (English Generalized Cognitive Hierarchy Theory , GCHT ) is a further development of the CHT by Chong, Ho and Camerer. It represents the most recently published model from the level-k argumentation area . In comparison to their original theory, the authors have added two parameters to improve the accuracy of the predictions.

The parameter captures the tendency of the players to experience distortion through stereotyping . This means that, especially in situations of strong cognitive stress or exhausted cognitive capacities, individuals are tempted to simplify or reduce their assumptions by stereotyping information, i.e. grouping it on the basis of common typical properties, in order to increase the effectiveness of information processing and the decision-making process to increase (see also out-group homogeneity ). Applied to the level-k argument , this means that players, as in the CHT , include all lower types of players in their decision-making process, but the relative distribution of the lower levels is only correctly determined if . The higher the parameter , the more players focus on the most common lower types of players. ${\ displaystyle \ textstyle \ alpha}$ ${\ displaystyle \ textstyle (\ geq 1)}$ ${\ displaystyle \ textstyle \ alpha = 1}$ ${\ displaystyle \ textstyle \ alpha}$

The parameter supports a changed specification of the level 0 behavior. The common assumptions of a randomly acting level 0 player or a level 0 player who experiences an attraction through the prominent action are replaced by the fact that this type of player is reluctant to receive the minimum payout in the GCHT . In short, level 0 players still act non-strategically, but they are able to choose actions that never result in the smallest possible payout for any strategy of the opponent with a higher probability ( ) than the action that will give the least Payout results. In contrast to the assumption of randomly acting level 0 players, the GCHT suggests that every player selects non-dominated actions more often than dominated actions . ${\ displaystyle \ textstyle \ beta}$ ${\ displaystyle \ textstyle (\ geq 1)}$ ${\ displaystyle \ textstyle \ beta}$

The generalized theory of the cognitive hierarchy includes both the original CHT and a modified form of the classic level-k reasoning , in which higher types of players find a best answer to the most frequently occurring lower level (and not necessarily to the next lower level).

For and there is the theoretical framework of the theory of cognitive hierarchy : players are able to correctly specify the relative distribution of the lower types of players and level 0 players follow the assumption of random action. ${\ displaystyle \ textstyle \ alpha = 1}$ ${\ displaystyle \ textstyle \ beta = 1}$

For and there is the theoretical framework of the modified form of the level-k argumentation : players assume that the other players belong to a single lower player type, and level-0 players follow the assumption of random action. ${\ displaystyle \ textstyle \ alpha = \ infty}$ ${\ displaystyle \ textstyle \ beta = 1}$

Level-k reasoning in dynamic games

The level-k reasoning has at times been applied almost exclusively to games in normal form , such as the beauty pageant . Games in extensive form have therefore not yet been studied much in theory. However, even with these games, a different behavior of the players is often observed. A classic example of this is the millipede game by Robert W. Rosenthal.

Centipede Game

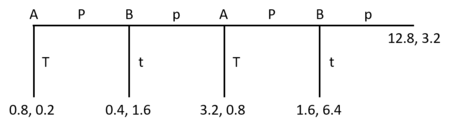
Play tree of a 4-round millipede game. The money pot doubles in the next round if A or B increases it in their round (P or p). If a player ends the game in his round (T or t), he receives 80% of the money pot and the other player receives the remaining 20%.

In Tausendfüßlerspiel (English Centipede game ) Two players decide alternately, if they want to increase a constantly growing pot of money ( "Pass" ) or whether they want to end the game ( "Take" to keep) to a larger share of the money pot. In this example the players are called A and B. A decides first and also receives the larger share if B decides to raise the money pot in the last round.

The standard solution for the millipede game is determined by backward induction . In the final round, B will compare his two possible payouts and end the game instead of increasing the pot, as this will maximize his payout.

Categorization of the player types in the 4-round millipede game. R stands for random action by a player, P stands for raising the money pot and T stands for ending the game.

In the penultimate round, A knows that B will end the game in the last round. So he decides to end the game instead of increasing the pot in order to maximize his potential payout. This process is repeated iteratively and ends with the subgame-perfect Nash equilibrium , in which A ends the game in his first round.

Therefore, standard theory predicts that all players will quit the game as soon as they have the opportunity, despite the higher payouts that would result from more cooperative trading. However, such cooperative behavior is regularly observed in experiments - even if only for a limited number of rounds. While the benefits of cooperation remain (and even grow), most games are ended halfway through the rounds by a player who was previously cooperative.

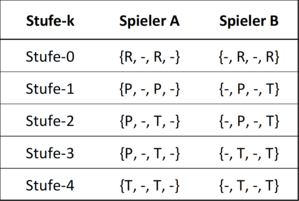
Assuming that a level 0 player acts randomly, i.e. increases the pot of money or ends the game with the same probability for each of his decisions, the behavior of the players observed in experiments corresponds to the level 2 and level 3 player types for player A. or level 3 and level 4 for player B.

Dynamic Level-k Model

With the k-stage dynamic model (English Dynamic Level-k model ) have Teck-Hua Ho and Xuanming Su made the first an attempt to stage-k reasoning applied to dynamic games. The authors assume that a level 0 player at each decision point with the same probability either increases the money pot or ends the game. A higher player type always finds the best answer to the next lower player type.

In the context of extensive forms of play, it is important to define a player's strategy for all decision points. Accordingly, Ho and Su make the assumption that a player would also end the game at all further decision points from the point in time at which he first decided to end the game. This assumption is justified by the fact that it does not matter which decision is made at later decision points, since these are never reached.

In the dynamic level-k model, the players form initial guesses about the player type of the other players. Based on this initial guess, players then find a best answer. The authors emphasize that their theory, in comparison to the classic models of level-k argumentation and the CHT, does not include the heterogeneity of the player types, but the heterogeneity of the assumptions about the player types of the other players.

Additionally, in this dynamic approach, players are able to update their initial guesses between repetitions of the same game using Bayes' theorem . This models that players are able to learn from the experiences they have gathered and to adapt both their guesses and their actions accordingly.

Compared to the classic forms of level-k argumentation and the CHT , Ho and Su highlight three fundamental differences.

Players are not limited in their cognitive abilities in the dynamic level-k model . This means that every player is capable of capturing every type of player at any time.
Closely related to this is the assumption that players do not necessarily assume that they belong to the highest level of all players. In the dynamic level-k model , players may well perceive that there are higher types of players within the population, but still maintain their actions, as they suspect that the majority of players are of a lower type than their own.
Updating the guesses is probably the clearest differentiating feature, as this enables a player to adapt to the observed behavior of the other players. If a player encounters mainly higher types of players, he will choose the actions of a higher level himself, but if he encounters mainly lower types of players, he will himself choose the actions of a lower level.

Individual evidence

↑ ^a ^b ^c ^d ^e ^f Nagel, Rosemarie. "Unraveling in Guessing Games: An Experimental Study". American Economic Review , 85 (5): 1313-1326. 1995
↑ ^a ^b ^c ^d ^e ^f ^g ^h Stahl, Dale O., and Paul W. Wilson. " On Players' Models of Other Players: Theory and Experimental Evidence ". Games and Economic Behavior . 10 (1): 218-254. 1995
↑ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Camerer, Colin F., Teck-Hua Ho and Juin-Kuan Chong. " A Cognitive Hierarchy Model of Games ". Quarterly Journal of Economics . 119 (3): 861-898. 2004
↑ Camerer, Colin F. "Behavioral Game Theory". Princeton University Press . 2003
↑ ^a ^b ^c ^d ^e ^f ^g ^h Burchardi, Konrad B. and Stefan P. Penczynski. "Out of Your Mind: Eliciting Individual Reasoning in One Shot Games". Games and Economic Behavior . 84: 39-57. 2014
↑ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l Ho, Teck-Hua and Xuanming Su. " A Dynamic Level-k Model in Sequential Games ". Management Science . 59 (2): 452-469. 2013
↑ ^a ^b ^c ^d ^e Kawagoe, Toshiji, and Hirokazu Takizawa. "Level-k Analysis of Experimental Centipede Games". Journal of Economic Behavior & Organization . 82 (2-3): 548-566. 2009
^ ^A ^b ^c Costa-Gomes, Miguel and Vincent P. Crawford. "Cognition and Behavior in Two-Person Guessing Games: An Experimental Study". American Economic Review . 96 (5): 1737-1768. 2006
↑ Crawford, Vincent P., and Nagore Iriberri. "Fatal Attraction: Salience, Naivete, and Sophistication in Experimental Hide-and-seek Games". American Economic Review . 97 (5): 1731-1750. 2007
↑ Crawford, Vincent P., and Nagore Iriberri. "Level-k Auctions: Can a Nonequilibrium Model of Strategic Thinking Explain the Winner's Curse and Overbidding in Private-Value Auctions?". Econometrica . 75 (6): 1721-1770. 2007
↑ ^a ^b ^c ^d ^e ^f ^g Chong, Juin-Kuan, Teck-Hua Ho, and Colin Camerer. " A Generalized Cognitive Hierarchy Model of Games ". Games and Economic Behavior , 99: 257-274. 2016
^ ^A ^b Arad, Ayala and Ariel Rubinstein. "The 11-20 Money Request Game: A Level-K Reasoning Study". American Economic Review . 102 (7): 3561-3573. 2012
^ ^A ^b Costa-Gomes, Miguel, Vincent P. Crawford, and Bruno Broseta. "Cognition and Behavior in Normal-form Games: An Experimental Study". Econometrica . 69 (5): 1193-1235. 2001
^ Bosch-Domènech, Antoni, José G. Montalvo, Rosemarie Nagel, and Albert Satorra. "One, Two, (Three), Infinity, ...: Newspaper and Lab Beauty-contest Experiments". American Economic Review . 92 (5): 1687-701. 2002
↑ Arad, Ayala. " The Tennis Coach Problem: A Game-theoretic and Experimental Study ". BE Journal of Theoretical Economics . 12 (1): Article 10. 2012
↑ Nagel, Rosemarie. "A Survey on Experimental Beauty Contest Games: Bounded Rationality and Learning". in Budescu, David V., Ido Erev and Rami Zwick (eds.). "Games and Human Behavior: Essays in Honor of Amnon Rapoport". Lawrence Erlbaum Associates . 105-142. 1999
^ Rosenthal, Robert W. " Games of Perfect Information: Predatory Pricing and the Chain-Store Paradox ". Journal of Economic Theory . 25 (1): 92-100. 1981
^ Aumann, Robert J. " On the Centipede Game ". Games and Economic Behavior . 23 (1): 97-105. 1998
↑ McKelvey, Richard D., and Thomas R. Palfrey. "An Experimental Study of the Centipede Game". Econometrica . 803-836. 1992

[Nagel-1] ↑ ^a ^b ^c ^d ^e ^f Nagel, Rosemarie. "Unraveling in Guessing Games: An Experimental Study". American Economic Review , 85 (5): 1313-1326. 1995

[StahlWilson-2] ↑ ^a ^b ^c ^d ^e ^f ^g ^h Stahl, Dale O., and Paul W. Wilson. " On Players' Models of Other Players: Theory and Experimental Evidence ". Games and Economic Behavior . 10 (1): 218-254. 1995

[CamererHoChong-3] ↑ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Camerer, Colin F., Teck-Hua Ho and Juin-Kuan Chong. " A Cognitive Hierarchy Model of Games ". Quarterly Journal of Economics . 119 (3): 861-898. 2004

[Camerer-4] Camerer, Colin F. "Behavioral Game Theory". Princeton University Press . 2003

[BurchardiPenczynski-5] ↑ ^a ^b ^c ^d ^e ^f ^g ^h Burchardi, Konrad B. and Stefan P. Penczynski. "Out of Your Mind: Eliciting Individual Reasoning in One Shot Games". Games and Economic Behavior . 84: 39-57. 2014

[HoSu-6] ↑ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l Ho, Teck-Hua and Xuanming Su. " A Dynamic Level-k Model in Sequential Games ". Management Science . 59 (2): 452-469. 2013

[KawagoeTakizawa-7] Kawagoe, Toshiji, and Hirokazu Takizawa. "Level-k Analysis of Experimental Centipede Games". Journal of Economic Behavior & Organization . 82 (2-3): 548-566. 2009

[CostaGomesCrawford-8] A ^b ^c Costa-Gomes, Miguel and Vincent P. Crawford. "Cognition and Behavior in Two-Person Guessing Games: An Experimental Study". American Economic Review . 96 (5): 1737-1768. 2006

[9] Crawford, Vincent P., and Nagore Iriberri. "Fatal Attraction: Salience, Naivete, and Sophistication in Experimental Hide-and-seek Games". American Economic Review . 97 (5): 1731-1750. 2007

[10] Crawford, Vincent P., and Nagore Iriberri. "Level-k Auctions: Can a Nonequilibrium Model of Strategic Thinking Explain the Winner's Curse and Overbidding in Private-Value Auctions?". Econometrica . 75 (6): 1721-1770. 2007

[ChongHoCamerer-11] ↑ ^a ^b ^c ^d ^e ^f ^g Chong, Juin-Kuan, Teck-Hua Ho, and Colin Camerer. " A Generalized Cognitive Hierarchy Model of Games ". Games and Economic Behavior , 99: 257-274. 2016

[AradRubinstein-12] A ^b Arad, Ayala and Ariel Rubinstein. "The 11-20 Money Request Game: A Level-K Reasoning Study". American Economic Review . 102 (7): 3561-3573. 2012

[CostaGomesEtAl-13] A ^b Costa-Gomes, Miguel, Vincent P. Crawford, and Bruno Broseta. "Cognition and Behavior in Normal-form Games: An Experimental Study". Econometrica . 69 (5): 1193-1235. 2001

[BoschDomènechEtAl-14] Bosch-Domènech, Antoni, José G. Montalvo, Rosemarie Nagel, and Albert Satorra. "One, Two, (Three), Infinity, ...: Newspaper and Lab Beauty-contest Experiments". American Economic Review . 92 (5): 1687-701. 2002

[Arad-15] Arad, Ayala. " The Tennis Coach Problem: A Game-theoretic and Experimental Study ". BE Journal of Theoretical Economics . 12 (1): Article 10. 2012

[16] Nagel, Rosemarie. "A Survey on Experimental Beauty Contest Games: Bounded Rationality and Learning". in Budescu, David V., Ido Erev and Rami Zwick (eds.). "Games and Human Behavior: Essays in Honor of Amnon Rapoport". Lawrence Erlbaum Associates . 105-142. 1999

[Rosenthal-17] Rosenthal, Robert W. " Games of Perfect Information: Predatory Pricing and the Chain-Store Paradox ". Journal of Economic Theory . 25 (1): 92-100. 1981

[Aumann-18] Aumann, Robert J. " On the Centipede Game ". Games and Economic Behavior . 23 (1): 97-105. 1998

[McKelveyPalfrey-19] McKelvey, Richard D., and Thomas R. Palfrey. "An Experimental Study of the Centipede Game". Econometrica . 803-836. 1992