Term logic
Term logic , also called traditional logic or conceptual logic in philosophy , describes the logic that began with Aristotle and which was dominant until the late 19th century, when modern predicate logic emerged.
In order to understand philosophical texts that arose before the development of predicate logic (e.g. the medieval or Leibniz 'and Kant's logic), a basic knowledge of the terminology and the ideas of term logic are indispensable.
Aristotle's system
Aristotle's work is summarized in the six texts that are collectively referred to as the Organon . Two of these texts in particular, the Analytica priora and De Interpretatione, contain the core of his logic, the study of judgments and conclusions .
The basics
The basic assumption of the theory is that judgments (also statements or sentences ; English propositions ) are composed of two terms - hence the name term logic - and that the process of inference is based on judgments:
- The term is that part of a speech that means something in itself, such as human or mortal , but which means nothing that can be true or false.
- The judgment (Greek apophansis ): a combination of two terms that indicates or announces something that can be true or false. The judgment contains two terms, one term, the predicate , of which the other term, the subject , is affirmative or negative .
- The syllogism is an inference in which one judgment (the conclusion ) necessarily follows from two others (the premises ).
The term
The term (Greek horos , Latin terminus ) is the basic component of the judgment. The original meaning of horos and also of terminus is boundary (Latin determinatio ). Terms mean concepts and delimit meanings. The two terms are on the edge of the judgment, connected by the act of affirmation or negation.
For Aristotle a term is simply a thing , a part of the judgment. For early modern logicians such as Arnauld (whose Port-Royal logic was the most famous logic text of his time), Leibniz and Kant, terms stand for terms, ideas or concepts .
The fact that subject and predicate have equal rights in classical interpretations and can also change places within different judgments is important both for understanding traditional terminology and for its appropriate translation into modern formalisms: the term human can occur as a subject (if, for example, he is assigned the predicate white ) and as a predicate (e.g. if the term Greek is assigned the predicate human or the term horse is denied this predicate).
The judgment
In term logic, a (categorical) judgment (or: a sentence, a proposition) is a special type of sentence in which the subject term and the predicate term are linked so that - in a corresponding interpretation - something true or false is stated. There are four different types of judgments, namely the A, I, E, and O judgments, and these types of judgments are classified according to their quality and quantity ( cf.quantity and quality of judgments ):
The logical quality of a judgment can be affirmative (if the predicate is affirmed by the subject) or negative (if the predicate is denied to the subject).
The quantity of a judgment says whether it is total (or general ) (the predicate is assigned or denied to "the whole", Greek Catholicou , of the subject) or particular (Greek meros ; the predicate is only assigned to part of the subject - or agreed).
With the help of these terms, the following classification results:
| general | particular | |
|---|---|---|
| affirmative | A judgment | I judgment |
| negative | E judgment | O judgment |
If there are terms, then the four judgments are usually written in the form ; however, other spellings are also common.
In words one reads these judgments as follows:
| A judgment | SaP | All S are P |
|---|---|---|
| I judgment | SiP | Some S are P |
| E judgment | SeP | No S is P |
| O judgment | SoP | Some S are not P |
This way of speaking is problematic for the following reason: It seems to take for granted that an extensional interpretation is presupposed (see the section Intensional and Extensional Interpretation ); that is, an interpretation in which S and P stand for sets of individuals . Now you can - albeit somewhat unusual in the German language - also choose an intensive way of speaking (for example: P comes to S; or: the term S contains the term P), but that would not solve the problem that the syntax of the Term logic does not need a semantic definition at all, but - however you speak - such a definition of standard semantics always resonates.
The conclusion (syllogism)
Aristotle set up a sophisticated theory of logical inference based on individual rules of inference, the syllogisms (see the detailed description in General Presentation of the Syllogism ).
He assumes perfect syllogisms:
“If three terms are related to one another in such a way that the last (the sub-term) is in the middle as a whole, and the middle is either or not in the first (the generic term) as a whole, then there is a necessary one for the outer terms perfect end. ... Because if A is predicted by every B and B by every C, A must be predicated by every C. ... Likewise, if A is stated by no B, but B is stated by every C, A cannot belong to any B. "
In formula notation, these rules can be written as follows:
- CaA follows from CaB and BaA.
- CeA follows from CaB and BeA.
This system also includes conversions such as
- AeB follows BeA.
- AiB follows BiA.
- AaB follows BiA.
Aristotle illustrated the latter rule (referred to as subalternation) through the following example:
"If every pleasure is a good, then some good must also be a pleasure."
Algebraic term logic
In the course of the algebraization of logic in the 19th century, George Boole's first mathematical logic calculus emerged in 1847 as a formalization of Aristotelian term logic. Calculations by his successors John Venn , Ernst Schröder and Charles Sanders Peirce were also part of this term logic tradition. The older attempts at formalizing the logic of terms by Leibniz around 1690 were published as early as 1840, but only influenced the term calculi by Giuseppe Peano .
Term logic and predicate logic
The modern predicate logic, founded in 1879 by the conceptual writing by Gottlob Frege , contains an interpretation of the term logic, as it is still often given today.
| judgment | translation |
|---|---|
| SaP | |
| SeP | |
| SiP | |
| SoP |
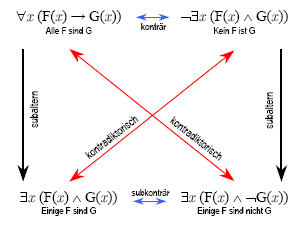
In his conceptual writing, Frege sketched the classic judgment square as follows (we use today's notation):
This Fregesche formalization, which has been adopted from almost all current textbooks, has the disadvantage that it does not reflect important properties of term logic. For example, the subalternation (the arrow on the far left in the sketch) is valid in Aristotle's term logic:
but not in Fregesch's "translation" into predicate logic:
Attempts have been made to remedy this problem by modifying the Fregesch formulas. Strawson discusses several possibilities; including the following:
The Fregesche formulation of the universal judgment is expanded to include an existence assumption :
The idea behind it is that in the case of a “non-empty set of subjects” the subalternation applies - which is certainly correct. Strawson states, however, that this change has undesirable consequences for the entire system - the subalternation is now valid, but other, previously correct laws are no longer correct. His attempts to save the Fregesche predicate logic formulation prove unsuccessful.
The Polish logician Stanisław Jaśkowski has proven that there is no meaningful formalization of term logic by means of the (monadic) first-order predicate logic . Klaus Glashoff has confirmed these results with computer-aided evidence.
Decline of term logic
Predicate logic prevailed in the 20th century. At the same time, the term logic with the associated syllogistics fell more and more out of use; it was practiced almost exclusively in the field of philosophy. Term logic also survived in the context of traditional Roman Catholic theological training.
Modern term logic
The most important development of term logic in recent times is John Corcoran's formalization of Aristotelian logic through natural deduction in 1973. The forerunner is Jan Łukasiewicz , who in his book gave the first termological formalization of Aristotelian logic. Both systems have the advantage that the entire Aristotelian syllogistics can be derived without additional assumptions that Aristotle does not have (existence assumptions). In contrast to Corcoran, Łukasiewicz used propositional logic in his formalization of Aristotelian logic , which has been criticized frequently since then and can be avoided through Corcoran's work. Corcoran's theory is valued by philosophers and historians of logic because the evidence through Natural Inference reproduces almost verbatim Aristotle's reasoning in his Analytica priora .
In the following, the formal elements of the modern, Corcoran terminology are described.
Calculus of modern term logic
building blocks
The atoms of the term logic consist of
- the four characters A, I, E, O . They designate the classic four Aristotelian forms of judgment ;
- the countably many term constants (or simply terms) . It's also easier to write .
The variables of the term logic are denoted with , and this is sometimes also used . These variables are also called term variables .
There is a single rule of formation ; it says that strings of the form Aab, Iab, Eab, Oab are allowed; here a and b can be any term constants (including ... etc.).
Strings of the form Uab (where U is one of the atoms A, I, E, O and a, b are arbitrary terms) are referred to as judgments , Aristotelian statements , or, for short, just statements . They are the actual building blocks of the term logic.
Term logic has no axioms . This means that the rules discussed in the following section always apply to assumptions . In particular, it follows from this that there are no tautologies in this logic .
However, there is a variant of the term logic presented here, in which all expressions of the form Aaa are axioms.
The following language has become common for the judgments:
- Aab: All a are b
- Iab: Some a are b
- Eab: No a is b
- Oab: Not all a are b
There are many different representations of judgments in the literature; for example - for our Aab - also aAb or A (a, b) .
Transformation rules
The transformation rules belonging to the calculus of term logic are as follows:
- Example: With the help of these rules, the assumptions can e.g. B. derive the conclusion as follows:
- From is derived from R2
- From is derived from R4
In this case you write .
Intensional and extensional interpretation
In his doctrine of the inference in the Analytica priora, Aristotle has already denoted terms in general, with etc. This opens up the possibility of operating purely syntactically with these term constants, and it is the precondition for a calculus-based investigation of his term logic.
Regardless of the syntactic issues that are in the foreground in most investigations into term logic, the semantics of Aristotelian term logic have long been discussed; d. H. about the question of what exactly the term constants mean (or: what they denote, what they stand for). There are two different possibilities here: the extensional and the dimensional semantics.
Extensional semantics
In this semantics, one assumes that the term constants stand for non-empty sets (collections of individuals). According to this, "man" stands for the totality of all people, and "Greek" stands for the multitude of all Greeks. Semantics based on this interpretation are also referred to as scope logic .
The dimensional semantics
Here the term constants are interpreted as terms . Each concept has other, further concepts as content; z. B. the term “gold” has the term “metal” as content. This example comes from Leibniz , who clearly described the two ways of interpreting the logic of terms.
Which semantics are historically correct?
The question of which interpretation - intensional or extensional - Aristotle had in mind in his Analytica Priora has been much debated; Individual authors claim that the doctrine of the difference between extension and intention can already be found in Aristotle and that medieval authors had already discussed this difference. What is certain is that these terms were treated in the logic of Port-Royal by Antoine Arnauld and then later in detail and in a very formal framework by Leibniz and compared with one another as equivalent, Leibniz preferring the dimensional interpretation:
“I have preferred, however, to look at the universal concepts or ideas and their summary, because they do not depend on the existence of individuals. ... Our expressions and those of the schools ... must, however, be carefully distinguished. "
Recently , based on the work of Gottfried Wilhelm Leibniz , Klaus Glashoff gave an intensive semantics with the corresponding completeness theorem .
literature
- Christoph Horn , Christof Rapp (Hrsg.): Dictionary of ancient philosophy . Beck, Munich 2002, ISBN 3-406-47623-6 , pp. 501 .
- Otfried Höffe (Ed.): Aristoteles Lexicon (= Kröner's pocket edition . Volume 459). Kröner, Stuttgart 2005, ISBN 3-520-45901-9 , p. XV, 640.
- Raili Kauppi: About Leibniz's logic with special consideration of the problem of intension and extension. In: Acta Philosophica Fennica. Fasc. XII, Helsinki 1960.
- Joseph Maria Bocheński : Ancient Formal Logic. North Holland 1951.
- Louis Couturat : La Logique de Leibniz. Olms, Hildesheim 1961 (1901).
- Peter Geach : Reason and Argument. University of California Press, 1976.
- NGL Hammond, HH Scullard (eds.): The Oxford Classical Dictionary . Oxford University Press, 1992, ISBN 0-19-869117-3 .
- George Hayward Joyce: Principles of Logic. ( Memento of February 27, 2006 in the Internet Archive ) 3rd edition. Longmans, 1949 (1908). (A manual for use in Catholic seminaries. Reference work on traditional logic, with many references to medieval and ancient sources. Contains no references to modern logic. The author lived from 1864 to 1943).
- Jan Łukasiewicz : Aristotle's Syllogistic, from the Standpoint of Modern Formal Logic. Oxford Univ. Press, 1951.
- John Stuart Mill : A System of Logic. 8th edition. London 1904.
- William Thomas Parry, Edward A. Hacker: Aristotelian Logic. State University of New York Press, 1991.
- Arthur Norman Prior : Formal Logic. Oxford University Press, 2nd edition 1962. (Mainly on modern formal logic; however, the text contains quite a bit of term logic and medieval logic).
- Arthur Norman Prior: The Doctrine of Propositions and Terms. Ed. Peter Geach , AJP Kenny. Duckworth, London 1976.
- Willard Van Orman Quine : Philosophy of Logic. 2nd Edition. Harvard University Press, 1986.
- Lynn E. Rose: Aristotle's Syllogistic. Thomas, Springfield 1968.
- Fred Sommers: The Calculus of Terms. In: Mind 79, 1970, pp. 1–39. Reprinted in: G. Englebretsen (Ed.): The new syllogistic. Lang, New York 1987, ISBN 0-8204-0448-9 .
- Fred Sommers: The logic of natural language. Oxford University Press, 1982.
- Fred Sommers: Predication in the Logic of Terms. In: Notre Dame Journal of Formal Logic. 31, 1990, pp. 106-126.
- Fred Sommers, George Englebretsen: An invitation to formal reasoning. The logic of terms. Ashgate, Aldershot 2000, ISBN 0-7546-1366-6 .
Web links
- Robin Smith: Aristotle's Logic. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
- Terence Parsons : Traditional Square of Opposition. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
- (Editor): Aristotle: Logic. In: Internet Encyclopedia of Philosophy .
- Aristotle's term logic online , online program for experimentation and research on Aristotelian logic
- Aristotelian Logic on PlanetMath
Individual evidence
- ↑ The Romans translated apophansis with enuntiatio , propositio and iudicum . Statement is a recent translation of enuntiatio . Iudicum occurs mainly in Boethius and was introduced into German by Leibniz as a "judgment" and naturalized by Wolff . English logic has always spoken of proposition .
- ↑ Immanuel Kant: Writings on metaphysics and logic. Work edition Volume VI. Edited by Wilhelm Weischedel. Suhrkamp, ISBN 3-518-27789-8 , p. 521.
- ↑ Doctrine of Conclusion or First Analytics. First Book, Chapter 4, p. 25.
- ↑ Doctrine of Conclusion or First Analytics. First Book, Chapter 2, p. 25.
- ^ Peano, G: Logique mathématique. In: Peano: Formulaire de mathématique , Tome II, Turin 1897, p. 18 list of quotations, most of the quotations from: GW Leibnitii Opera philophophica , ed. Erdmann, Berlin 1840.
- ^ PF Strawson: Introduction to Logical Theory. Methuen & Co., New York and London 1952. pp. 125 ff.
- ^ Stanisław Jaśkowski: On the interpretations of Aristotelian categorical propositions in the predicate calculus. In: Studia Logica. 24, pp. 161-172 (1969).
- ^ Klaus Glashoff : On the translation of the Aristotelian logic into the predicate logic .
- ↑ Frederick Copleston: A History of Philosophy. Image Books 1993-1994, ISBN 0-385-46843-1 .
- ↑ John Corcoran: Completeness of an Ancient Logic. In: The Journal of Symbolic Logic. Volume 37, No. 4, December 1973.
- ↑ Jan Łukasiewicz: Aristotle's syllogistic. From the standpoint of modern formal logic. Clarendon Press, Oxford 1951.
- ↑ George Boger: Completion, Reduction and Analysis: Three Proof-theoretic Processes in Aristotle's Prior Analysis. In: History and Philosophy of Logic. 19, 1998, pp. 187-226.
- ^ Aristotle: Doctrine of the conclusion or first analytics (Organon III). Meiner, Hamburg 1992, ISBN 3-7873-1092-4 .
- ↑ A. Hamacher-Hermes: Content or scope logic? Alber, Freiburg, Munich 1994, ISBN 3-495-47792-6 .
- ↑ Gottfried Wilhelm Leibniz: Complete writings and letters. Row 6: Philosophical Writings. Volume 4, 1677-1690, Part A, N. 1, N. 56 - N. 64 and N. 72. Akademie-Verlag, Berlin 1999.
- ↑ Ellen Walther-Klaus: Content and scope - studies on the validity and history of the reciprocity of extension and intention. Hildesheim, Zurich, New York 1987.
- ↑ z. B. Joseph C. Frisch: Extension and Comprehension in Logic. New York 1969.
- ↑ Gottfried Wilhelm Leibniz: Complete writings and letters. Row 6: Philosophical Writings. Volume 4, 1677-1690, Part A, N.1, N. 56 - N. 64 and N. 72, Akademie-Verlag, Berlin 1999.
- ^ Klaus Glashoff: An intensional Leibniz Semantics for Aristotelian Logic . In: The Review of Symbolic Logic. 3, 2010, p. 262, doi: 10.1017 / S1755020309990396 .