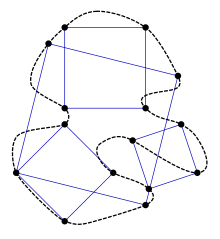
Toeplitz conjecture

Example: The black dashed line goes through all the corner points of the various blue squares.

The Toeplitz conjecture is an unsolved question from geometry : Does every closed Jordan curve contain all corner points of a square ? In some special cases, the assumption has already been solved, for example if the curve is convex or piecewise smooth . The problem was first described by Otto Toeplitz in 1911. The first positive results were found by Arnold Emch and Lew Genrichowitsch Schnirelman . The general case is open (2016).

definition

Be a closed Jordan curve . A polygon is inscribed, if all the vertices of to include. The Toeplitz conjecture reads: ${\displaystyle C}$ ${\displaystyle P}$ ${\displaystyle C}$ ${\displaystyle P}$ ${\displaystyle C}$

Every closed Jordan curve has an inscribed square.

It is not necessary that the corner points of the square appear in a certain order.

Examples

Some geometric representations, such as circles and squares , allow an infinite number of inscribed squares. If C is an obtuse triangle , then there can be exactly one inscribed square, for right triangles there can be exactly two, and acute triangles allow exactly three.

Solved cases

An obvious approach would be to solve the inscribed square problem by proving that a special class of closed curves always contains an inscribed square and then approximating an arbitrary curve by a series of closed curves and concluding that there is an inscribed square as There is a limit to the number of squares that can be written into the curve sequence. One reason this line of reasoning has not been advanced is that the limit of a sequence of squares need not necessarily be a square, but can also be a single point.

Pieces of analytical curves

Emch (1916) has shown that piecewise analytical curves always have inscribed squares. This is particularly true of polygons . Emch's proof considers the curves formed by the midpoints of those secants that are parallel to a given line. It shows that if these curves are intersected with the curves generated in the same way for a perpendicular family of secants, an odd number of intersection points are obtained. Therefore there is always at least one point of intersection which forms the center of a diamond inscribed in the curve . By continuously rotating the two perpendicular straight lines and using the intermediate value theorem , he shows that at least one of these diamonds is a square.

Locally monotonous curves

Walter Stromquist has proven that every locally monotonous plane simple curve allows an inscribed square. The condition of local monotony has the consequence that for each point p the curve C can be represented locally as a graph of the function . More precisely: for every point on there is an environment and a fixed direction (the direction of the " axis"), so that no chord of in this environment is parallel to . Locally monotonic curves include all polygons , all closed convex curves, and all piecewise C ¹ -curves with no apex. ${\displaystyle y=f(x)}$ ${\displaystyle p}$ ${\displaystyle C}$ ${\displaystyle U(p)}$ ${\displaystyle n(p)}$ ${\displaystyle y}$ ${\displaystyle C}$ ${\displaystyle n(p)}$

Curves without specially trapezoids

A weaker condition for the curve than the local monotony is that for some the curve has no inscribed so-called "special trapezoids" of size . A special trapezoid is the trapezoid with three sides of equal length, each of which is longer than the fourth side. The corner points of the trapezoid are arranged on the curve in such a way that their sequence corresponds to that of a clockwise passage through the curve. The size of the trapezoid is understood to be the length of the part of the curve that corresponds to the course along the three sides of the trapezoid of equal length. Its size is part of the curve that is expanded by the three sides of the same length. If there are no such trapezoids (or an even number of them), a boundary crossing can be carried out and it can be shown that the curves always have an inscribed square. ${\displaystyle \varepsilon >0}$ ${\displaystyle \varepsilon }$

Curves in a circular ring

If a Jordan curve lies in a circular ring , the outer radius of which is at most- times the inner radius, and the curve is drawn in such a way that it separates the inner circle from the outer, then it has an inscribed square. If this curve can be approximated by a closed curve, then all "large" squares that contain the center of the annulus and are inscribed in this approximation are topologically separated from the squares that do not contain the center of the annulus. Again, the limit of the sequence of large squares must be a large square and not collapse into a single point. Therefore the limit value theorem may be applied. ${\displaystyle (1+{\sqrt {2}})}$

Symmetrical curves

Centrally symmetric curves also have inscribed squares, even fractals such as the Koch curve .

Variants and generalization

One can ask oneself whether other forms can also be written into any Jordan curve. It is known that for every triangle and every closed Jordan curve there is too similar a triangle inscribed in. In addition, the set of vertices of such triangles is a dense subset in the curve . Above all, there is always an equilateral inscribed triangle. It is also known that every closed Jordan curve allows an inscribed rectangle . ${\displaystyle \Delta }$ ${\displaystyle C}$ ${\displaystyle \Delta }$ ${\displaystyle C}$

Some generalizations of the Toeplitz conjecture consider inscribed polygons for curves and even general continua in higher dimensional Euclidean spaces . Stromquist has shown, for example, that every continuous closed curve im , which satisfies the condition that no two circular chords are perpendicular to each other in a suitable neighborhood of any point, allows an inscribed quadrilateral with equal sides and equal diagonals. This class of curves includes all curves. Nielsen and Wright have proven that every symmetric continuum in includes many inscribed rectangles. HW Guggenheimer showed that each hypersurface -diffeomorph to the sphere is vertices of a regular hypercube includes. ${\displaystyle C}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle C}$ ${\displaystyle C^{2}}$ ${\displaystyle K}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle C^{3}}$ ${\displaystyle S^{n-1}}$ ${\displaystyle 2n}$

Individual evidence

1. ^ O. Toeplitz : About some tasks of Analysis situs . In: Negotiations of the Swiss Society for Natural Research in Solothurn . 94, 1911, p. 197.
2. ^ Emch: On some properties of the medians of closed continuous curves formed by analytic arcs, American Journal of Mathematics, Volume 38, 1916, pp. 6-18
3. ↑ Lev Šnirel'man: On Certain geometrical properties of closed curves . In: Akademiya Nauk SSSR i Moskovskoe Matematicheskoe Obshchestvo. Uspekhi Matematicheskikh Nauk . 10, 1944, pp. 34-44.
4. ^ Terence Tao : An integration approach to the Toeplitz square peg problem . 22nd November 2016.
5. ^ Herbert Bailey: Squares inscribed in angles and triangles . In: Mathematics Magazine . 71, 1998, pp. 278-284.
6. ^ Benjamin Matschke: A survey on the square peg problem . In: Notices of the American Mathematical Society . 61, 2014, pp. 346-253. doi : 10.1016 / 0033-5894 (85) 90074-2 .
7. ^ Benjamin Matschke: A survey on the square peg problem . In: Notices of the American Mathematical Society . 61, 2014, pp. 346-253. doi : 10.1016 / 0033-5894 (85) 90074-2 .
8. ^ Walter Stromquist: Inscribed squares and square-like quadrilaterals in closed curves . In: Mathematika . 36, 1989, pp. 187-197. doi : 10.1112 / S0025579300013061 .
9. ^ Benjamin Matschke: A survey on the square peg problem . In: Notices of the American Mathematical Society . 61, 2014, pp. 346-253. doi : 10.1016 / 0033-5894 (85) 90074-2 .
10. ^ Benjamin Matschke: A survey on the square peg problem . In: Notices of the American Mathematical Society . 61, 2014, pp. 346-253. Doi : 10.1016 / 0033-5894 (85) 90074-2 .
11. ^ Mark Nielsen, SE Wright: Rectangles inscribed in symmetric continua . In: Geometriae Dedicata . 56, 1995, pp. 285-297. doi : 10.1007 / BF01263570 .
12. ↑ Mark D. Meyerson: Equilateral triangles and continuous curves . In: Fundamenta Mathematicae . 110, 1980, pp. 1-9.
13. ^ EH Kronheimer, PB Kronheimer: The tripos problem . In: Journal of the London Mathematical Society . 24, 1981, pp. 182-192. bibcode : 1985QuRes..23 ... 87O . doi : 10.1112 / jlms / s2-24.1.182 .
14. ^ Mark Nielsen, SE Wright: Rectangles inscribed in symmetric continua . In: Geometriae Dedicata . 56, 1995, pp. 285-297. doi : 10.1007 / BF01263570 .
15. ^ Walter Stromquist: Inscribed squares and square-like quadrilaterals in closed curves . In: Mathematika . 36, 1989, pp. 187-197. doi : 10.1112 / S0025579300013061 .
16. ^ Mark Nielsen, SE Wright: Rectangles inscribed in symmetric continua . In: Geometriae Dedicata . 56, 1995, pp. 285-297. doi : 10.1007 / BF01263570 .
17. ^ H. Guggenheimer: Finite sets on curves and surfaces . In: Israel Journal of Mathematics . 3, 1965, pp. 104-112. doi : 10.1007 / BF02760036 .

literature

• Victor Klee and Stan Wagon , Old and New Unsolved Problems in Plane Geometry and Number Theory , The Dolciani Mathematical Expositions, Number 11, Mathematical Association of America , 1991

Web links

• Mark J. Nielsen, Figures Inscribed in Curves. A short tour of an old problem
• Inscribed squares: Denne speaks at Jordan Ellenberg's blog