Three-phase traffic theory

The three-phase traffic theory is an alternative traffic theory , founded by Boris Kerner in the years 1996–2002. It explains the collapse of traffic and the resulting congested traffic on expressways . Kerner describes three phases of traffic, whereas the classical theories based on the fundamental diagram of traffic flow include two phases: free traffic and congested traffic . The congested traffic is divided by Kerner into two phases, synchronized traffic and moving wide traffic jam , which then result in a total of three phases:

Synchronized traffic

Traffic jam

1. Free traffic ( F )
2. Synchronized traffic ( S )
3. Moving Wide Jam ( J )

A phase is defined as a state in space and time .

Free traffic ( F )

Figure 1: Data measurements of traffic flow in relation to traffic density with free traffic (fictitious data)

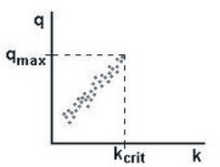
Most of the time, drivers can freely choose their speed in free traffic . Empirical data show a positive relationship between traffic flow (in vehicles per unit of time ) and traffic density (in vehicles per unit of length). This relationship is limited by a maximum point of free traffic at a maximum flow with a corresponding critical density (Figure 1). ${\displaystyle q}$ ${\displaystyle k}$ ${\displaystyle q_{\mathrm {max} }}$ ${\displaystyle k_{\mathrm {crit} }}$

Congested traffic

Figure 2: Data measurements of traffic flow in relation to traffic density in free and congested traffic (fictitious data)

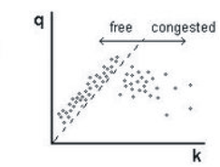
In congested traffic, empirical data show a less clear relationship between flow and density. Therefore Kerner concludes that the fundamental diagram, which is used in classical traffic theory, cannot adequately describe the complex dynamics of traffic. Instead, it divides the congested traffic into synchronized traffic and moving wide traffic jams . In congested traffic, the vehicle speed is lower than the minimum vehicle speed in free traffic. The line with the gradient , which corresponds to the minimum vehicle speed for free traffic (dotted line in Figure 2), divides all empirical data on the flow-density level into two areas: data on the left correspond to free traffic, data on the right the jammed (English: congested) traffic. ${\displaystyle v_{\mathrm {free} }^{\mathrm {min} }}$ ${\displaystyle v_{\mathrm {free} }^{\mathrm {min} }={\frac {q_{\mathrm {max} }}{k_{\mathrm {crit} }}}}$

Definitions [ J ] and [ S ] of phases J and S in congested traffic

In Kerner's theory, the phase definitions [ J ] and [ S ] for congested traffic are the result of the generally applicable empirical temporal-spatial properties of the traffic data. The phases J and S are defined by the definitions [ J ] and [ S ] as follows:

Figure 3: Generally valid temporal-spatial properties of traffic disruptions and their connection with Kerner's three-phase traffic theory. Measurement data of the velocities in time and space (a) and their representation in the time-space plane (b)

The traffic phase "moving wide traffic jam" [ J ]

A “wide moving jam” moves upstream through all the bottlenecks. The mean speed of the downstream traffic jam is maintained. Phase J is defined on the basis of this characteristic property of large moving traffic jams . ${\displaystyle v_{g}}$

The term moving wide traffic jam is intended to reflect the characteristic property of the traffic jams in question to move through all other traffic conditions and all bottlenecks while maintaining the speed of the downstream traffic jam. The term moving traffic jam reflects that the traffic jam is moving as a whole localized structure on the road. Kerner uses the term broadly to distinguish between moving traffic jams and other moving traffic jams that do not necessarily maintain the mean speed of the downstream traffic jams . The term broad reflects the following fact: If the width (i.e. extent along the road) of a moving traffic jam is significantly greater than the width of the front of the traffic jam and if the vehicle speed is zero inside the traffic jam, then the traffic jam always remains the same Speed ​​of the downstream congestion front at (see Section 7.6.5 of the book). Thus, the term broad does not mean the width across the traffic jam, but refers to the fact that the entire traffic jam has a significantly greater length than the transition areas at both ends. Historically, Kerner used the term broadly in qualitative analogy to broad autosolitons that occur in many systems from the natural sciences (such as gas plasma, electron-hole plasma in semiconductors, biological systems, and chemical reactions): Both broad moving congestion as broad autosolitons also have characteristic properties that do not depend on the initial conditions under which these localized structures were formed.

The traffic phase "Synchronized traffic" [ S ]

In “synchronized traffic”, the downstream front, where the vehicles accelerate when entering free traffic, does not show the characteristic property of wide moving traffic jams. In particular, the downstream front of Synchronized Traffic is often attached to a bottleneck. Synchronized traffic is characterized by a continuous flow of traffic with no significant standstill, as often occurs in moving wide traffic jams.

The term “synchronized traffic” is intended to reflect the following properties of this traffic phase: On the one hand, there is a tendency towards the synchronization of vehicle speeds in different lanes. In addition, there is a tendency to synchronize the vehicle speeds in the individual lanes (group formation of vehicles). This is due to a low probability of overtaking.

Explanation of the phase definitions [ J ] and [ S ] with empirical measurement data

The definitions [ J ] and [ S ] are illustrated in Figure 3 (a) by real measurement data for the mean vehicle speed. There are two different temporal-spatial structures of congested traffic with low vehicle speeds in Figure 3 (a). A structure of the congested traffic propagates upstream with almost constant speed of the downstream front through the narrow point on the expressway. According to the definition [ J ], this structure of the congested traffic belongs to the traffic phase “moving wide congestion”. In contrast, the downstream front of the other structure of the congested traffic is fixed at the narrow point. According to the definition [ S ], this structure of the congested traffic belongs to the traffic phase “synchronized traffic” (Figs. 3 (a) and (b)). Other examples for the empirical validation of the traffic phase definitions [ J ] and [ S ] are in the books and, in the article as well as an empirical study of floating car data (floating car data are also called sample vehicle data ).

Definition of the traffic phases based on individual vehicle data

In section 6.1. The book shows that the traffic phase definitions [ J ] and [ S ] are the starting point for most hypotheses of three-phase traffic theory and related microscopic traffic flow models. The traffic phase definitions [ J ] and [ S ] are non-local, macroscopic definitions and can only be used after macroscopic data have been measured in space and time, that is, in "offline" investigations. This is because, in order to clearly differentiate between traffic phases J and S , it is necessary to examine how congested traffic moves at a bottleneck using the definitions [ J ] and [ S ]. This is often seen as a disadvantage of the traffic phase definitions [ J ] and [ S ]. However, there are also microscopic criteria for distinguishing phases J and S without examining the propagation of congested traffic through a bottleneck. The microscopic criteria are as follows (see Section 2.6 in the book): If an "interruption of the flow of traffic" is observed in individual vehicle data ( microscopic data ) of congested traffic, i. H. a time gap between two successive vehicles, which is much larger (the latter is approximately 1.3 to 2.1 s) than the average time delay in accelerating from a wide moving traffic jam, then the interrupt corresponds to the phase of the traffic flow J . Were found with this criterion all the wide moving traffic jams, all other states include the congested traffic of the phase J on.

Kerner's hypothesis about the two-dimensional (2D) area of ​​homogeneous states of synchronized traffic in the flow-density plane

Hypothetical homogeneous states of synchronized traffic

A homogeneous state of synchronized traffic (English: “a steady state of synchronized flow”; hereinafter referred to as “homogeneous synchronized traffic”) is a hypothetical state of synchronized traffic of the same vehicles and drivers moving at the same time-independent speed and at the same intervals (the distance is the net distance between two consecutive vehicles). This means that this synchronized traffic is homogeneous in time and space.

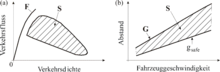
Kerner's hypothesis reads as follows: Conditions of homogeneous synchronized traffic cover a two-dimensional area in the flow-density plane (2D area “S” in Fig. 4 (a)). The set of possible states of free traffic overlaps the set of states of homogeneous synchronized traffic. The states of free traffic on a multi-lane expressway and the states of homogeneous synchronized traffic are separated at a given traffic density by a gap in the flow of traffic and, consequently, by a gap in speed: at each individual traffic density the speed in synchronized homogeneous traffic is less than in free traffic.

In accordance with this hypothesis of Kerner's three-phase traffic theory, a driver can make any choice of the distance to the vehicle in front at a given speed in synchronized traffic . This is possible within a certain range of distances corresponding to the two-dimensional area of ​​the homogeneous synchronized traffic conditions (Fig. 4 (b)): a driver accepts different distances at different times and does not steer towards a fixed distance to the vehicle in front.

Figure 4: Hypothesis of Kerner's three-phase traffic theory over the two-dimensional area of ​​homogeneous states of synchronized traffic in the flow-density level: (a) Qualitative representation of states of free traffic (F) and the two-dimensional area of ​​the states of the homogeneous synchronized traffic (dashed area S) on a multi-lane expressway in the river density level. (b) Part of the two-dimensional region of the states of homogeneous synchronized traffic from (a) in the distance-speed plane (dashed region S). In (b) is the synchronization distance of the traffic and is the safety distance between two vehicles following one another. ${\displaystyle G}$ ${\displaystyle g_{\mathrm {safe} }}$

The hypothesis of Kerner's three-phase traffic theory about the 2D area of ​​homogeneous synchronized traffic contradicts previous traffic flow theories about the fundamental diagram of traffic , which assume a one-dimensional relationship between traffic density and traffic flow.

Vehicle following behavior in three-phase traffic theory

According to Kerner's three-phase traffic theory, a vehicle accelerates to the vehicle in front if the distance is greater than a synchronization distance , i.e. H. at (referred to as "vehicle acceleration" in Fig. 5). A vehicle decelerates when its distance is less than a safe distance , i.e. H. at (referred to as "vehicle deceleration" in Fig. 5). ${\displaystyle g}$ ${\displaystyle G}$ ${\displaystyle g>G}$ ${\displaystyle g}$ ${\displaystyle g_{\mathrm {safe} }}$ ${\displaystyle g<g_{\mathrm {safe} }}$

Figure 5: Qualitative representation of the vehicle following behavior in Kerner's three-phase traffic theory: a vehicle accelerates at distances and decelerates at , while under the condition it adapts its speed to that of the vehicle in front without paying attention to the exact spatial distance. The dashed area of ​​the synchronized traffic is taken from Fig. 4 (b). ${\displaystyle g>G}$ ${\displaystyle g<g_{\mathrm {safe} }}$ ${\displaystyle g_{\mathrm {safe} }\leq g\leq G}$

If the distance to the vehicle in front is less than the synchronization distance , the driver adapts his speed to the speed of the vehicle in front without paying attention to the exact distance. This applies as long as this distance is not smaller than the safety distance (referred to as "speed adjustment" in Fig. 5). Accordingly, in the vehicle following behavior according to Kerner's three-phase traffic theory, the distance can assume any value in the range . ${\displaystyle g}$ ${\displaystyle G}$ ${\displaystyle g_{\mathrm {safe} }}$ ${\displaystyle g}$ ${\displaystyle g_{\mathrm {safe} }\leq g\leq G}$

Traffic collapse - an F → S phase transition

In the measurement data, the congested traffic usually arises at a bottleneck in an expressway, such as an entrance , an exit or a construction site . Such a transition from free to congested traffic is known as a traffic breakdown (i.e., traffic breakdown). In Kerner's three-phase traffic theory, a traffic collapse is explained by an F → S phase transition . This explanation is confirmed by available measurement data, since in measurements of the traffic after a traffic collapse at a bottleneck, the downstream flank of the congested traffic is fixed at the bottleneck. Therefore, the congested traffic resulting from a traffic breakdown corresponds to the definition [ S ] for the traffic phase “synchronized traffic”.

Empirical spontaneous and induced F → S phase transitions

Using empirical measurement data, Kerner establishes that synchronized traffic can develop spontaneously (spontaneous F → S phase transition) or induced from outside (induced F → S phase transition) in free traffic.

A spontaneous F → S phase transition means that a traffic collapse occurs if there was previously free traffic both at the bottleneck and downstream and upstream of the bottleneck. This means that a spontaneous F → S phase transition occurs through the growth of an intrinsic disturbance in free traffic.

In contrast, an induced breakdown is caused by disruptions in the flow of traffic that originally occurred at a different location. This is usually related to an upstream expansion of a synchronized traffic area or a wide moving congestion. An empirical example of the induced traffic collapse at a bottleneck, which leads to synchronized traffic, can be seen in Figure 3: The movement of a wide traffic jam through the bottleneck creates synchronized traffic. The existence of empirically induced traffic crashes (i.e. empirically induced F → S phase transitions) means that F → S phase transitions occur in metastable free traffic states. The term “metastable free traffic” means that the state of free traffic is stable to small disturbances; H. in the case of minor disruptions, free traffic continues at the narrow point. However, if major disruptions occur near a bottleneck in free traffic, the free traffic is unstable and synchronized traffic occurs at the bottleneck.

Physical explanation of the traffic collapse in the three-phase theory

Figure 6: To explain the traffic collapse by a Z-type nonlinear jump-type function of the overtaking probability in Kerner's three-phase traffic theory. The dashed curve shows the critical overtaking probability as a function of traffic density.

Kerner explains the nature of the F → S phase transition on the basis of a competition between "speed adaptation" and "over-acceleration". Speed ​​adaptation is defined as the deceleration of a vehicle to the speed of the slower vehicle in front. Over-acceleration is defined as the acceleration of a vehicle whose vehicle in front is neither moving faster nor accelerating. In Kerner's theory, the probability of over-acceleration is a discontinuous function of the vehicle speed: for a given vehicle density, the probability of over-acceleration in free traffic is greater than in synchronized traffic. If in free traffic within a local disturbance of the speed the speed adjustment is predominant compared to the over-acceleration, an F → S phase transition takes place. If, on the other hand, the over-acceleration outweighs the speed adaptation, the disturbance subsides over time. In a synchronized traffic area, strong over-acceleration is responsible for a reverse transition from synchronized traffic to free traffic (S → F transition).

Vehicle over-acceleration can occur through several possible mechanisms. It can be assumed that on a multi-lane expressway, changing to a faster lane is the most likely mechanism of over-acceleration. In this case, F → S phase transitions are explained by the interplay of acceleration when overtaking a slower vehicle (over-acceleration) and deceleration to the speed of the slower vehicle in front (speed adjustment). Overtaking supports the continuation of free traffic. “Speed ​​adjustment”, on the other hand, leads to synchronized traffic. Such a speed adjustment takes place when overtaking is not possible. Kerner assumes that the probability of overtaking is an interrupted function of the vehicle density (Figure 6): for a given vehicle density, the probability of overtaking in free traffic is significantly greater than in synchronized traffic.

Discussion of Kerner's explanation of the traffic collapse

Kerner's explanation of the traffic collapse at bottlenecks in expressways by an F → S phase transition is related to the following fundamental empirical properties of the traffic collapse at bottlenecks, as observed in real measurement data: (i) Spontaneous traffic collapses in the free traffic at the entrance lead to the occurrence of congested traffic Traffic whose downstream front is fixed at the bottleneck (at least for a certain time interval), d. H. this congested traffic satisfies the definition [ S ] for the traffic phase of synchronized traffic. In other words: spontaneous traffic breakdown is always an F → S phase transition. (ii) The probability of spontaneous traffic collapse is an increasing function of the traffic flow at the bottleneck. (iii) At the same bottleneck, a traffic breakdown can be either spontaneous or induced (see the empirical examples of these basic characteristics of traffic breakdown in Sections 2.2.3 and 3.1. of the book); for this reason the F → S phase transition occurs in metastable free traffic.

The reason for Kerner's theory and his criticism of classical traffic theories

The basic empirical properties (i) - (iii) of the traffic collapse cannot be explained by classical traffic theories and models. The search for explanations of these fundamental empirical properties of the traffic collapse was the reason for the development of Kerner's three-phase traffic theory. In particular, in two-phase traffic models in which the traffic collapse is related to an instability of the free flow, this instability leads to an F → J phase transition. In other words, in these traffic models, the traffic collapse is determined by the spontaneous occurrence of large moving traffic jams in the entrance free traffic (see Kerner's criticism of such two-phase models and other classic traffic models and theories in Chapter 10 of the book as well as in the critical one Review article).

Infinite number of road capacities

In the three-phase traffic theory, the fundamental empirical properties of the traffic collapse are explained by an F → S phase transition that occurs in metastable free traffic. Probably the most important consequence of this is the existence of a margin of road capacity between a maximum and a minimum capacity.

Maximum and minimum road capacity

Figure 7: Maximum and minimum road capacities in Kerner's three-phase traffic theory

A spontaneous traffic breakdown, i. H. a spontaneous F → S phase transition can occur in a wide range of traffic flows in free traffic. Using empirical measurement data that shows that both a spontaneous and an induced traffic collapse is possible at the same bottleneck on an expressway, Kerner determines that an infinite number of road capacities exist at any point in time . This infinite number of road capacities lie between a minimum road capacity and a maximum road capacity for free traffic (Fig. 7). ${\displaystyle C_{\mathrm {min} }}$ ${\displaystyle C_{\mathrm {max} }}$

Road capacities and metastability of free traffic

If the traffic flow in free traffic is close to the maximum road capacity, even small disturbances in free traffic at a bottleneck lead to a spontaneous F → S phase transition. In contrast, with a traffic flow close to the minimum road capacity, only very large disruptions in free traffic at a bottleneck can lead to a spontaneous F → S phase transition (cf. e.g. Section 17.2.2 of the book). However, the likelihood of a minor disruption in free traffic is much greater than that of a major disruption. Therefore, the greater the flow of traffic in free traffic at the bottleneck, the greater the probability of the spontaneous F → S phase transition. If the traffic flow in free traffic is less than the minimum road capacity , no traffic collapse (F → S phase transition) can take place at the bottleneck, i.e. H. free movement is stable. ${\displaystyle C_{\mathrm {max} }}$ ${\displaystyle C_{\mathrm {min} }}$ ${\displaystyle C_{\mathrm {min} }}$

The infinite number of road capacities can be due to the metastability of free traffic when traffic flows in the area ${\displaystyle q}$

${\displaystyle C_{\mathrm {min} }\leq q<C_{\mathrm {max} }}$

be clarified. Metastability of free traffic means that in the event of minor disruptions the traffic status can still be stable (free traffic remains), but in the event of larger disruptions the free traffic becomes unstable and an F → S phase transition to synchronized traffic then takes place.

Discussion of the definitions of road capacity

The basic theoretical understanding of the three-phase traffic theory about the stochastic capacity of free traffic at a bottleneck is as follows: At any point in time there is an infinite number of road capacities for free traffic at a bottleneck. The infinite number of traffic flows at which a traffic collapse can be induced at a bottleneck corresponds to the infinite number of road capacities. These capacities lie within the range of traffic flows between a minimum and a maximum capacity (Fig. 7). The infinite number of road capacities of Kerner's three-phase traffic theory fundamentally contradicts the classic understanding of stochastic road capacity as well as the classic traffic theories and methods for traffic management and traffic control , in which the existence of a certain road capacity is assumed at all times . In contrast, in Kerner's three-phase traffic theory, there is an infinite number of road capacities at any one time , which are within the above-mentioned range between the minimum road capacity and the maximum road capacity. The values of and can considerably different traffic parameters depend (percentage share of trucks , weather, characteristics of effective bottleneck, etc.). The existence of a range of road capacities at any point in time according to Kerner's theory has a decisive effect on the methods of traffic control, dynamic traffic allocation and traffic management. In particular, in order to satisfy the fundamental empirical properties of traffic collapse , Kerner introduced the breakdown minimization principle (BM principle) for optimizing and controlling road traffic networks . ${\displaystyle C_{\mathrm {min} }}$ ${\displaystyle C_{\mathrm {max} }}$ ${\displaystyle C_{\mathrm {min} }}$ ${\displaystyle C_{\mathrm {max} }}$

Moving wide jams ( J )

A moving traffic jam is called "wide" if its length (in the direction of travel of the road) clearly exceeds the length of the front of the traffic jam. The average speed of the vehicles within the wide moving traffic jam is significantly lower than the average speed in free traffic. At the downstream traffic jam, the vehicles accelerate again to the speed possible in free traffic or in synchronized traffic. On the upstream front, the vehicles are coming out of free traffic or synchronized traffic and have to reduce their speed. According to the definition [ J ], a moving wide traffic jam maintains the average speed of the downstream traffic jam front , even if the traffic jam moves through other traffic phases or bottlenecks. The flow of traffic (number of vehicles per unit of time) is very much reduced within a wide moving traffic jam. ${\displaystyle v_{g}}$

Characteristic parameters of moving wide congestion

Figure 8: The three traffic phases in the river density level in Kerner's three-phase traffic theory

Kerner's empirical results show that some characteristic parameters of moving wide traffic jams are independent of the traffic volume and the properties of a bottleneck (e.g. where and when a traffic jam occurred). However, these characteristic parameters can strongly depend on weather conditions, road conditions, vehicle technology, proportion of long vehicles, etc. The speed of the downstream congestion front of a moving wide congestion (in the upstream direction ) is a characteristic parameter, as is the traffic flow downstream of the downstream congestion front (with free traffic at this point, see Figure 8). This means that multiple moving wide jams will have similar characteristics under similar conditions. For these reasons, these parameters are predictable to a certain extent. The movement of the downstream damming front can be represented in the flow density plane by a line called “Line J” (Line J in Figure 8). The slope of line J is equal to the speed of the downstream congestion front . ${\displaystyle v_{g}}$ ${\displaystyle q_{\mathrm {out} }}$ ${\displaystyle v_{g}}$

Minimal road capacity and drainage from moving wide congestion

Kerner emphasizes that the minimum road capacity and the outflow from a wide moving traffic jam correspond to two qualitatively different properties of free traffic : The minimum road capacity is a characteristic of the F → S phase transition at a bottleneck (i.e., the traffic collapse). On the other hand, the discharge from a moving wide impoundment characterizes the conditions of existence and formation of the impoundment, i.e. H. the traffic phase J , while the traffic jam moves through free traffic. A wide moving traffic jam that moves through free traffic can only continue if the congestion inflow is greater than the congestion outflow , otherwise the congestion will dissolve over time. Depending on traffic parameters (such as weather, proportion of trucks in the traffic flow, etc.) and on the characteristics of the bottleneck where the F → S phase transition takes place, the minimum road capacity can either be smaller than the congestion discharge (as shown in Fig. 8) or also bigger than his. ${\displaystyle C_{\mathrm {min} }}$ ${\displaystyle q_{\mathrm {out} }}$ ${\displaystyle C_{\mathrm {min} }}$ ${\displaystyle q_{\mathrm {out} }}$ ${\displaystyle q_{\mathrm {in} }}$ ${\displaystyle q_{\mathrm {out} }}$ ${\displaystyle C_{\mathrm {min} }}$ ${\displaystyle q_{\mathrm {out} }}$ ${\displaystyle q_{\mathrm {out} }}$

Synchronized traffic ( S )

In contrast to moving wide traffic jams, both the traffic flow and the speeds of the vehicles can vary considerably within the traffic phase of the synchronized traffic. The downstream front of the synchronized traffic is often fixed at a certain point along the road (see definition [ S ]), usually at a bottleneck. The flow of traffic in this phase can still be comparable to the flow of traffic in free traffic even if the speeds of the vehicles are significantly reduced. Since synchronized traffic does not have the characteristic congestion property of phase J of moving wide congestion, it is assumed in Kerner's three-phase traffic theory that hypothetical homogeneous states of synchronized traffic form a two-dimensional area in the flow density plane (dashed areas in picture 8).

S → J phase transition

Large moving traffic jams do not arise spontaneously in free traffic, but can arise spontaneously in synchronized traffic areas. This phase transition is called the S → J phase transition.

"Jam out of nowhere" - F → S → J phase transitions

Figure 9: Empirical example of a cascade of F → S → J phase transitions according to Kerner's three-phase traffic theory: (a) Phase transitions in space and time. (b) Representation of the same phase transitions as in (a) in the speed-density plane (the arrows S → F, J → S and J → F show possible phase transitions).

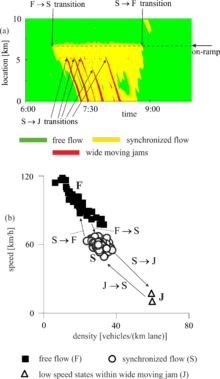
In 1998, Kerner found out that the occurrence of a wide moving traffic jam in free traffic can be observed in real traffic data as a cascade of F → S → J phase transitions (Figure 9): First, synchronized traffic occurs in an area of ​​free traffic. As explained above, such an F → S phase transition occurs mostly at a bottleneck in the expressway. Then this synchronized traffic “self-compression” takes place, the traffic density increases, the speed decreases further. This self-compression is called the “pinch effect”. In these pinch areas of synchronized traffic, narrow moving traffic jams arise. As these moving narrow jams grow, they become moving wide jams, which is indicated by S → J in Figure 9. Thus, wide moving traffic jams arise later and at a different point on the road than the traffic collapse (F → S phase transition) took place. Therefore, one should pay attention to the representation of the traffic phase transitions occurring in real traffic (Fig. 9 (a)) in the speed-density level (Fig. 9 (b)) (or the speed-traffic flow level or traffic flow-density level) that the synchronized traffic conditions and the low speed conditions in the moving wide congestion were measured at different locations on the road. Kerner notes that the higher the density of synchronized traffic, the higher the frequency of occurrence of moving wide traffic jams. These moving wide congestion travel upstream even as they pass through synchronized traffic areas or other bottlenecks. Obviously, all combinations of reverse phase transitions (transitions S → F, J → S and J → F in Fig. 9) are possible.

Physics of the S → J phase transition

To further clarify the S → J phase transition, it should be noted that in Kerner's three-phase traffic theory, line J divides the homogeneous states of synchronized traffic into two areas (Fig. 8). Homogeneous synchronized traffic states that are above line J are metastable . In contrast, the homogeneous synchronized traffic states that are below line J are stable . In these stable states, no S → J phase transition can take place. Metastable homogeneous synchronized traffic means that the traffic status is still stable in the event of small disturbances occurring, but the synchronized traffic becomes unstable in the case of larger disturbances and an S → J phase transition to a moving traffic jam can take place.

Traffic pattern from S and J

Very complex patterns of congested traffic caused by F → S and S → J phase transitions can be observed.

Classification of traffic patterns from S.

A synchronized flow pattern (SP) with a stationary downstream and a non- continuously propagating upstream front is called a localized synchronized flow pattern (LSP). However, it is often seen that the upstream front of an SP moves upstream. If only the upstream congestion front moves upstream, then this SP is called a widening synchronized flow pattern (WSP). The downstream front remains at the effective bottleneck and the expansion of the SP increases. It is also possible for both the upstream and downstream fronts to move upstream. The downstream front is then no longer fixed at the effective bottleneck. These patterns are called Moving Synchronized Flow Patterns (MSP).

“Capturing” of synchronized traffic at a bottleneck

The difference between an SP and a wide moving traffic jam is shown in the so-called “catch effect”, which can occur when a WSP or MSP reaches an upstream bottleneck. The SP is captured at the bottleneck and as a result a new congested traffic pattern is formed at this bottleneck. A wide moving traffic jam, on the other hand, is not caught at a bottleneck and continues to move upstream through the bottleneck. In contrast to moving wide congestion, Synchronized Traffic, even when moving as an MSP, has no characteristic parameters. For example, the velocity of the downstream front of an MSP can vary over a wide range and be different for different MSPs. These properties of SPs and moving wide congestion follow from the traffic phase definitions [ S ] and [ J ].

General congestion pattern (GP) - traffic pattern from S and J

Often jam patterns are observed, which include both traffic phases of congested traffic, both S and J . Such a traffic pattern from S and J is called a general congestion pattern (GP).

Figure 10: Measured traffic pattern EGP at three bottlenecks , and ${\displaystyle B_{1}}$ ${\displaystyle B_{2}}$ ${\displaystyle B_{3}}$

On many expressways, neighboring bottlenecks are often a short distance from one another. A congested traffic pattern in which the synchronized traffic comprises two or more bottlenecks in the road is called EP (EP: Expanded Pattern). An EP can consist exclusively of synchronized traffic (ESP: Expanded Synchronized Flow Pattern), but usually large moving traffic jams arise in synchronized traffic. In the latter case, the EP is known as EGP (EGP: Expanded General Pattern). An EGP consists of synchronized traffic as well as large moving traffic jams (Figure 10).

Applications of the three-phase theory

Figure 11: EGP traffic pattern in the ASDA / FOTO application in three countries

One of the applications often used Kerner the three-phase traffic theory are the methods ASDA / PHOTO ( A utomaticsearch S tau D ynamik A nalysis and F orecasting O f T raffic O bjects). ASDA / FOTO is a software tool that can process large amounts of traffic data quickly and efficiently, even for larger expressway networks (see examples from three countries, Figure 10). ASDA / FOTO is used in an online traffic system based on traffic measurements. To recognize, track and forecast the respective traffic phases S and J , the properties from Kerner's theory are used and implemented in the ASDA / FOTO models in a software tool that can process large amounts of traffic data quickly and efficiently, even in larger expressway networks ( see examples from three countries, Figure 10).

Other possible applications of the theory, which are described in the two books by Kerner, include the development of models for traffic simulation, for example, flow control (ANCONA), collective traffic control , driver assistance and traffic status detection in the vehicle.

Criticism of the theory

The theory has been criticized for two main reasons. First, the theory was based almost entirely on measurements taken on Federal Motorway 5 in Germany. It could therefore be that these patterns occur on this expressway, but other roads in other countries have different characteristics. So future research must show the validity of the theory on other roads in other countries of the world. Second, it is not clear how the data was interpolated. Kerner uses measurements at certain points along the road (loop detectors), but draws conclusions about vehicle trajectories that run along the entire length of the road under investigation. These trajectories can only be measured directly using floating car data, but, as stated, only measurements from loop detectors have been used. How the data was interpolated between the detector positions is not clear.

The above criticism was recently responded to with a study of data measured in the USA and the United Kingdom, which confirms the conclusions drawn from measurement results from Autobahn 5 in Germany. In addition, there is a more recent study of the theory based on floating car data, in which one can also find methods for the temporal-spatial interpolation of detector data (see the appendices to the article).

Other criticisms were made, such as B. that the concept of phase is not well defined, or that so-called two-phase models successfully reproduce the essential properties of traffic described by Kerner. The latter criticism was countered in a review article as follows: The most important property of Kerner's theory is its explanation of the fundamental empirical properties of the traffic breakdown caused by the F → S transition. The basic empirical properties of traffic breakdown cannot be explained with previous theories of traffic flow, including the two-phase models considered in. See the next section for more details.

Incommensurability of the three-phase traffic theory and classical theories of traffic flow

The explanation of the traffic collapse at a bottleneck by an F → S transition in metastable free traffic is the basic assumption of Kerner's three-phase theory. No previous theory includes the F → S transition in metastable free traffic at a bottleneck. Therefore, none of the classic theories of traffic flow is consistent with the empirical properties of traffic collapse at a narrow point on an expressway.

The F → S phase transition in metastable free traffic at a bottleneck explains the empirically proven induced transition from free to synchronized traffic together with the dependence of the probability of the breakdown on the traffic flow. In accordance with Kuhn's classic book, this shows the incommensurability of the three-phase theory and classic theories of traffic flow (more details can be found in):

The minimum road capacity at which an F → S phase transition can still be induced at a bottleneck according to Kerner's theory has no meaning for other theories and models of traffic flow. ${\displaystyle C_{\mathrm {min} }}$

The term “incommensurability” was introduced by Kuhn in his classic book to explain a paradigm shift in a scientific field.

Furthermore, it must be noted that the existence of the two phases F and S in the same traffic flow does not result from the stochastic nature of the traffic: even if there are no stochastic processes in the traffic, the states F and S exist in the same traffic flow. On the other hand, classic stochastic approaches to traffic control do not take into account the possibility of the F → S phase transition in metastable free traffic. For this reason, these stochastic approaches cannot solve the problem of the inconsistency of classical theories with the basic empirical properties of traffic breakdown.

According to Kerner, this inconsistency can explain why approaches to network optimization and traffic control that are based on these principles and methods have failed in practical application. Even decades of intensive efforts to improve and validate models for network optimization were unsuccessful. In fact, there are no examples that online implementations of the models for network optimization based on these principles and methods could reduce congested traffic in real traffic and transport networks.

This is due to the fact that the basic empirical properties of traffic breakdown at narrow passages of expressways have only been understood during the last 20 years. In contrast, the generally accepted principles and methods of transport and traffic theory were introduced in the 1950-1960s. Examples of these classic theories of traffic flow are the Lighthill-Whitham-Richards model (LWR), the General Motors traffic flow model (GM) by Herman, Gazis, Montroll, Potts, and Rothery, and Wardrop's principles of optimizing transportation networks. Therefore, the scientists whose ideas led to these classical foundations and methods of transport and traffic theory could not know the fundamental empirical properties of the traffic collapse. It should be noted that some of the diverse characteristics of driver behavior related to real traffic, as well as some mathematical approaches to traffic flow modeling, which are included in classical approaches to traffic flow theory, also in three-phase traffic theory and associated traffic flow models can be used (see section 11 of the review article for more details).

Individual evidence

1. ↑ ^{a b} Boris S. Kerner, "Experimental Features of Self-Organization in Traffic Flow", Physical Review Letters, 81, 3797-3400 (1998)
2. ↑ Boris S. Kerner, "The physics of traffic", Physics World Magazine 12, 25-30 (August 1999)
3. ↑ Boris S. Kerner, "Congested Traffic Flow: Observations and Theory", Transportation Research Record, Vol. 1678, pp. 160–167 (1999) ( Memento of the original from December 9, 2012 in the web archive archive.today ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this notice.  
4. ↑ ^{a b c d} B.S. Kerner, The Physics of Traffic , Springer, Berlin, New York 2004
5. ↑ BS Kerner, VV Osipov: Autosolitons . Springer, 1994, ISBN 978-94-017-0825-8 .
6. ↑ ^{a b c d e f} B.S. Kerner, Introduction to Modern Traffic Flow Theory and Control: The Long Road to Three-Phase Traffic Theory , Springer, Berlin, New York 2009
7. ^ ^{A b} Hubert Rehborn, Sergey L. Klenov, Jochen Palmer, "An empirical study of common traffic congestion features based on traffic data measured in the USA, the UK, and Germany". Physica A: Statistical Mechanics and its Applications, Volume 390, Issues 23-24, November 1, 2011, Pages 4466-4485.
8. ↑ R.-P. Schäfer et al., "A study of TomTom's probe vehicle data with three-phase traffic theory". Traffic Engineering and Control, Vol 52, No 5, Pages 225-231, 2011
9. ↑ ^{a b c d} Boris S. Kerner, "Criticism of generally accepted fundamentals and methodologies of traffic and transportation theory: A brief review", Physica A: Statistical Mechanics and its Applications 392, 5261-5282 (2013). doi : 10.1016 / j.physa.2013.06.004
10. ↑ Boris S. Kerner, Hubert Rehborn, Ralf-Peter Schäfer, Sergey L. Klenov, Jochen Palmer, Stefan Lorkowski, Nikolaus Witte. "Traffic dynamics in empirical probe vehicle data studied with three-phase theory: Spatiotemporal reconstruction of traffic phases and generation of jam warning messages" . Physica A: Statistical Mechanics and its Applications 392, 221-251 (2013).
11. ↑ ^{a b} M. Driver, A. Kesting, D. Helbing, "Three-phase traffic theory and two-phase models with a fundamental diagram in the light of empirical stylized facts". Transportation Research Part B: Methodological 44, 983-1000 (2010). doi : 10.1016 / j.trb.2010.03.004 .
12. ↑ ^{a b} T.S. Kuhn, "The structure of scientific revolutions". Fourth edition. (The University of Chicago Press, Chicago, London 2012)
13. ↑ Boris S. Kerner, Sergey L. Klenov, and Michael Schreckenberg, "Probabilistic physical characteristics of phase transitions at highway bottlenecks: Incommensurability of three-phase and two-phase traffic-flow theories" Phys. Rev. E 89, 052807 (2014). doi : 10.1103 / PhysRevE.89.052807
14. ^ MJ Lighthill and GB Whitham, "On kinematic waves: Theory of traffic flow on long crowded roads". Proc. Roy. Soc. A, 229, 281-345 (1955)
15. ^ Paul I. Richards: Shock Waves on the Highway. In: Operations Research. 4, 1956, p. 42, doi : 10.1287 / opre.4.1.42 .
16. ^ Robert Herman, Elliott W. Montroll, Renfrey B. Potts, Richard W. Rothery: Traffic Dynamics: Analysis of Stability in Car Following. In: Operations Research. 7, 1959, p. 86, doi : 10.1287 / opre.7.1.86 .
17. ^ Denos C. Gazis, Robert Herman, Richard W. Rothery: Nonlinear Follow-the-Leader Models of Traffic Flow. In: Operations Research. 9, 1961, p. 545, doi : 10.1287 / opre.9.4.545 .
18. ↑ JG WARDROP: ROAD PAPER. SOME THEORETICAL ASPECTS OF ROAD TRAFFIC RESEARCH .. In: Proceedings of the Institution of Civil Engineers. 1, 1952, p. 325, doi : 10.1680 / ipeds.1952.11259 .

Web links

• Physics Today - November 2005 by Henry Lieu (Federal Highway Administration, McLean, Virginia), Reviewer of the book "The Physics of Traffic: Empirical Freeway Pattern Features, Engineering Applications, and Theory" by Boris S. Kerner.
• Gao, K., Jiang, R., Hu, SX., Wang, BH. & Wu, QS "Cellular-automaton model with velocity adaptation in the framework of Kerner's three-phase traffic theory" Phys. Rev. E 76,026105 (2007).
• M. Schönhof, D. Helbing, "Criticism of three-phase traffic theory". Transportation Research Part B: Methodological 43 (7): 784-797 (2009). doi : 10.1016 / j.trb.2009.02.004 .
• H. Rehborn, S. Klenov, "Traffic Prediction of Congested Patterns", In: R. Meyers (Ed.): Encyclopedia of Complexity and Systems Science, Springer New York, 2009.
• H. Rehborn, J. Palmer, "Using ASDA and FOTO to generate RDS / TMC traffic messages", Traffic Engineering and Control, July 2008, pp. 261-266.
• LC Davis, A review on the book by BS Kerner "Introduction to Modern Traffic Flow Theory and Control" in Physics Today, Vol. 63, Issue 3 (2010), p. 53
• M. Driver, A. Kesting, D. Helbing, "Three-phase traffic theory and two-phase models with a fundamental diagram in the light of empirical stylized facts". Transportation Research Part B: Methodological 44, 983-1000 (2010). doi : 10.1016 / j.trb.2010.03.004 .
• H. Hartenstein, A review on the book by BS Kerner "Introduction to Modern Traffic Flow Theory and Control" in IEEE Vehicular Technology Magazine, Vol. 5, Issue 3 (2010), p. 91.

See also

• Fundamental diagram of traffic flow
• Traffic telematics
• Traffic flow
• Traffic jam
• ASDA / PHOTO
• Traffic model (traffic planning)