Rope statics

The design of suspension bridges , such as the Capilano suspension bridge , is achieved using rope statics.

The rope statics is a field of engineering mechanics that deals with the static of ropes or rope-like structures such as chains involved. Their behavior under static loads, which consist of individual forces , line loads or weight , is the subject of rope statics. Even wind loads may be significant that the collapse of the Tacoma Narrows Bridge in 1940 underscores dramatically.

Common applications for the rope statics for example, in cable cars , cable cranes , Public swimming or overhead lines and suspension bridges .

Properties of the ropes

Piece of a rope (black) loaded with a line load q with mechanical tensions σ _1.2 and resulting rope forces S _1.2 .

In the model representation of the rope static ropes are limp and dehnstarr . All structures to which these assumptions apply to a good approximation are idealized in the same way and collectively referred to as “ropes”.

Flexibility means that ropes can only transfer tensile forces that are tangential to the rope line as shown in the picture . Normal stresses (σ _1,2 , red), which are constantly distributed across its cross-section, act in the rope , the sum of which, the internal forces S _1,2 (blue), act perpendicular to the cross-section tangential to the rope fibers (black dash-dotted lines). The impression of shear transverse forces , bending and torsional moments is therefore excluded .

Extensibility means that the change in length of the rope under load is neglected or assumed to be insignificantly small. However, this only applies to tensile forces; ropes cannot absorb compressive forces in the axial direction.

The shear-free state of tension in ropes makes optimal use of the load-bearing behavior of materials. The rope lines determined in the rope statics deliver optimal designs for arches - support lines - under the given load.

General

Even if ropes cannot transfer transverse forces that are associated with shear, they can still absorb loads acting across the rope and transfer them to the rope suspension points, see picture.

a: suspension bridge, b: site plan of the bridge and c: cut of a piece of rope

Part a shows a suspension bridge spanning a valley. Part b is the site plan belonging to the bridge with the forces and dimensions acting on it. While the function y (x) defines the rope line, η (x) stands for the sag curve , which indicates the vertical distance between the rope and the connecting line of the suspension points. Part c shows a cut-free piece of the supporting rope . The rope force S and its horizontal and vertical components H and V, respectively on the positive right and negative left side of the cut, as well as the dimensions of the (infinitesimal) small piece of rope can be seen.

Rope line

The general equation for the rope line can be derived from figure c. If the line load q only acts in the vertical direction, as in the figure, the equilibrium in the x direction results in H (x + dx) - H (x) = 0, with the consequence:

Wenn die Streckenlast q nur in vertikaler Richtung wirkt, dann ist die Horizontalkomponente der Seilkraft konstant.

Because the load from dead weight and other weight forces is the most widespread, a load acting in the vertical direction is assumed below.

The equilibrium in the y-direction results in:

${\displaystyle V(x+\mathrm {d} x)-V(x)-q(x)\mathrm {d} x=0\quad \rightarrow \quad V'(x):=\lim \limits _{\mathrm {d} x\to 0}{\frac {V(x+\mathrm {d} x)-V(x)}{\mathrm {d} x}}=q(x).}$

Because the rope force works tangentially to the rope line everywhere, the slope of the rope line can also be expressed with the force components:

${\displaystyle y'={\frac {V}{H}}\quad \rightarrow \quad y''={\frac {V'}{H}}={\frac {q}{H}}.}$

The rope line provides twofold integration:

${\displaystyle y'(x)={\frac {1}{H}}\int _{0}^{x}q(\xi )\,\mathrm {d} \xi +C_{1}\quad \rightarrow \quad y(x)={\frac {1}{H}}\int _{0}^{x}\int _{0}^{x}q(\xi )\,\mathrm {d} \xi \mathrm {d} \xi +C_{1}x+C_{0}}$

The sag curve η (x) is the difference between the rope line and the straight line between the suspension points:

${\displaystyle \eta (x)=y(x)-{\frac {y_{L}-y_{0}}{L}}x-y_{0}\quad \rightarrow \quad \eta (0)=\eta (L)=0.}$

Here y _{0 is} the height of the bearing at x = 0 and y _{L is} the height of the bearing at x = L. The maximum sag is at

${\displaystyle \eta '(x)=y'(x)-{\frac {y_{L}-y_{0}}{L}}=0.}$

According to the mean value theorem of differential calculus, there is such a place between the suspension points. If the suspension points are not the same height, the lowest point of the sag curve is not where the rope has a horizontal tangent (at y '(x) = 0).

Rope forces

The rope forces result from the rope line

${\displaystyle V(x)=Hy'(x)\quad \rightarrow \quad S(x)={\sqrt {H^{2}+V^{2}(x)}}=H{\sqrt {1+y'(x)^{2}}}.}$

Die maximale Seilkraft ist dort, wo das Seil die betraglich größte Steigung hat, was in einem der Aufhängepunkte der Fall ist, sofern die Belastung des Seils überall nach unten wirkt.

The lowest point of the rope is either at the rope ends or where y '(x) = 0 applies, where the vertical pull V (x) has a zero crossing, the rope force is at a minimum and corresponds to the horizontal pull.

Adaptation to specifications

The previously available equations for the rope line and the rope forces do not provide any information about the integration constants C _0.1 or the horizontal pull H and are therefore not sufficient for the design of a rope in a specific application. With the three missing pieces mentioned, the rope line and the forces in the rope are clearly defined. The unknowns can of course be specified explicitly , but mostly they are specified implicitly by other information, for example by

• the maximum sag,
• the maximum rope force or
• the length of the cable between the suspension: . ${\displaystyle \textstyle l:=\int _{0}^{L}{\sqrt {1+y'(x)^{2}}}\,\mathrm {d} x}$

While the determination of the constant of integration is still relatively easy, the calculation of the horizontal pull is more difficult. In particular, the length of the rope, although an obvious specification, generally leads to a non-linear equation that has to be solved using numerical mathematics .

Rope under single load

Rope under the single load of a lantern that is suspended between two houses.

Under a point load that is negligible compared to the mass of the rope, the rope assumes a straight shape in sections, see picture. The lantern is held by two rope forces F _1,2 , seen from the lantern at an angle α or β to the horizontal . Equilibrium in x and y directions with the addition theorems at given angles α and β yields :

${\displaystyle {\begin{aligned}\sum _{i}F_{ix}=&F_{2}\cos \beta -F_{1}\cos \alpha =0\quad \rightarrow \quad F_{2}={\frac {\cos \alpha }{\cos \beta }}F_{1}\\\sum _{i}F_{iy}=&F_{1}\sin \alpha +F_{2}\sin \beta -G=F_{1}\sin \alpha +{\frac {\sin \beta \cos \alpha }{\cos \beta }}F_{1}-G=0\\\rightarrow F_{1}=&{\frac {G\cos \beta }{\sin(\alpha +\beta )}}\\F_{2}=&{\frac {G\cos \alpha }{\sin(\alpha +\beta )}}\end{aligned}}}$

If the lantern can move freely on a pulley on the rope, then it rolls into the equilibrium position α = β , where the rope forces F _{1,2 are} equal:

${\displaystyle F_{1}=F_{2}={\frac {G}{2\sin \alpha }}.}$

Rope under constant line load

A constant line load on a rope is a good approximation if

• the same load hangs on the rope, as on suspension bridges , at many equally distributed points,
• the rope has only a slight sag under its own weight or
• a ship pulls a weight through the water with a rope like a hand plummet .

With a constant line load q (x) = q ₀ , the above formula results in the rope line and sag curve

${\displaystyle {\begin{aligned}y'(x)=&{\frac {1}{H}}\int _{0}^{x}q_{0}\,\mathrm {d} \xi +C_{1}={\frac {q_{0}}{H}}x+C_{1}\\y(x)=&{\frac {1}{H}}\int _{0}^{x}\int _{0}^{x}q_{0}\,\mathrm {d} \xi \mathrm {d} \xi +C_{1}x+C_{0}={\frac {q_{0}}{2H}}x^{2}+C_{1}x+C_{0}\\\eta (x)=&-{\frac {q_{0}}{2H}}x(L-x).\end{aligned}}}$

With a constant line load, a parabolic rope line appears. The rope forces are:

${\displaystyle {\begin{aligned}V=&Hy'=q_{0}x+C_{1}H\\S=&H{\sqrt {1+y'^{2}}}={\sqrt {H^{2}+\left(q_{0}x+C_{1}H\right)^{2}}}\end{aligned}}}$

The rope length is calculated from the integral With the substitution and results ${\displaystyle \textstyle l=\int _{0}^{L}{\sqrt {1+y'(x)^{2}}}\,\mathrm {d} x.}$ ${\displaystyle z=y'(x)={\tfrac {2n}{L}}x+C_{1}}$ ${\displaystyle n={\tfrac {q_{0}L}{2H}}}$

${\displaystyle {\begin{aligned}l=&\int _{0}^{L}{\sqrt {1+y'(x)^{2}}}\,\mathrm {d} x=\int _{C_{1}}^{C_{1}+2n}{\sqrt {1+z^{2}}}{\frac {L}{2n}}\,\mathrm {d} z={\frac {L}{4n}}\left[\operatorname {arsinh} (z)+z{\sqrt {1+z^{2}}}\right]_{C_{1}}^{C_{1}+2n}\\=&{\frac {L}{4n}}\left[(C_{1}+2n){\sqrt {1+(C_{1}+2n)^{2}}}-C_{1}{\sqrt {1+C_{1}^{2}}}+\operatorname {arsinh} (C_{1}+2n)-\operatorname {arsinh} (C_{1})\right]\end{aligned}}}$

Here arsinh forms the inverse function of the hyperbolic sine . So now there are five equations for the rope forces, the rope line and length. The integration constants are determined by specifying their values ​​at certain points, especially at the suspension points. For example, if the left bearing at x = 0 at height y ₀ and the right bearing at x = L at height y _L , then the rope line is

${\displaystyle y(x)={\frac {q_{0}}{2H}}x^{2}+\left({\frac {y_{L}-y_{0}}{L}}-{\frac {q_{0}L}{2H}}\right)x+y_{0}}$

and the pitch:

${\displaystyle l={\frac {L}{4n}}\left[(m+n){\sqrt {1+(m+n)^{2}}}-(m-n){\sqrt {1+(m-n)^{2}}}+\operatorname {arsinh} (m+n)-\operatorname {arsinh} (m-n)\right].}$

This is the slope of the straight line connecting the suspension points. ${\displaystyle m={\tfrac {y_{L}-y_{0}}{L}}}$

If the horizontal pull H is also known, by direct specification or after calculation from another variable, all other forces and dimensions can also be determined. The determination of the horizontal pull is generally the biggest problem in the solution and the route over the rope length is, although complex, at least obvious. In any case, the solution is possible with numerical means.

Rope under its own weight

The load applied above the horizontal increases more and more towards the suspension points.

Forces (red) acting on the piece of rope (blue)

The dead weight is a constant load on ropes and is therefore particularly relevant. If there is only little sag, the line load of the rope is roughly constant due to its weight and the rope can be calculated as in the previous section. This view is forbidden with increasing sag, because the load applied above the horizontal increases more and more towards the suspension points, see small picture. In the cut piece of rope (large picture) equilibrium in the x-direction means:

Weil die Gewichtskraft vertikal zieht, ist der Horizontalzug konstant.

In the vertical direction, the weight d q = γ A d s , which is made up of the weight γ , the cross-sectional area A and the length d s , pulls on the piece of rope:

${\displaystyle {\begin{aligned}V(x+\mathrm {d} x)-\gamma A\mathrm {d} s-V(x)=&V(x+\mathrm {d} x)-\gamma A{\sqrt {\mathrm {d} x^{2}+\mathrm {d} y^{2}}}-V(x)\\=&V(x+\mathrm {d} x)-\gamma A{\sqrt {1+y'^{2}}}\mathrm {d} x-V(x)=0\\\rightarrow V':=&\lim \limits _{\mathrm {d} x\to 0}{\frac {V(x+\mathrm {d} x)-V(x)}{\mathrm {d} x}}=Hy''=\gamma A{\sqrt {1+y'^{2}}}\\\rightarrow y''=&{\frac {\gamma A}{H}}{\sqrt {1+y'^{2}}},\end{aligned}}}$

because the slope corresponds, as shown above, the ratio of the Vertikalzugs V to horizontal draft H . Twice integration provides the chain line expressed with the hyperbolic functions sinh and cosh

${\displaystyle y'=\sinh \left({\frac {\gamma A}{H}}x+C_{1}\right)\quad \rightarrow \quad y={\frac {H}{\gamma A}}\cosh \left({\frac {\gamma A}{H}}x+C_{1}\right)+C_{0}.}$

The length l of the rope is

${\displaystyle {\begin{aligned}l=&\int _{0}^{L}{\sqrt {1+y'^{2}}}\,\mathrm {d} x=\left[{\frac {H}{\gamma A}}\sinh \left({\frac {\gamma A}{H}}x+C_{1}\right)\right]_{0}^{L}={\frac {H}{\gamma A}}\sinh \left({\frac {\gamma A}{H}}L+C_{1}\right)-{\frac {H}{\gamma A}}\sinh(C_{1})\end{aligned}}}$

and the forces are in the rope

${\displaystyle V=Hy'=H\sinh \left({\frac {\gamma A}{H}}x+C_{1}\right)\quad {\text{und}}\quad S=H{\sqrt {1+y'^{2}}}=H\cosh \left({\frac {\gamma A}{H}}x+C_{1}\right)}$

Three of these equations to determine the unknown constants of integration C _0.1 and Horinzontalzugs H used. Non-linear, coupled equations will result, the solution of which is numerical.

Rope under single load and dead weight

Site plan of the rope and free body picture in point P

In the case of ropeways, neither the dead weight of the cable nor that of the cabin can be neglected, so it is necessary to combine single and dead weight as loads. The rope forces in front of and behind the force introduction point act tangentially to the rope and must be in balance with the point load. This is only possible if there is a kink in the rope line at the point of the individual force, which cannot be differentiated there , see picture. So the pieces of rope in front of and behind the individual force at point P must be considered separately.

The first piece of rope is treated in the x ₁ -y ₁ system and runs from the bearing in the origin to point P. The second piece of rope is given the x ₂ -y ₂ system, starts in P and ends in the bearing with the coordinates (L ₂ , y _L ). The common point P therefore has the coordinates (L ₁ , y ₁ ) in the left section and (0, y ₂ ) in the right. The rope lines derived in the previous section apply in both areas:

${\displaystyle {\begin{aligned}y_{1}=&{\frac {H_{1}}{\gamma A}}\cosh \left({\frac {\gamma A}{H_{1}}}x+C_{1}\right)+C_{0}\\y_{2}=&{\frac {H_{2}}{\gamma A}}\cosh \left({\frac {\gamma A}{H_{2}}}x+C_{3}\right)+C_{2}\end{aligned}}}$

The unknown horizontal pulls H _1,2 and integration _constants C _{0,1,2,3 are} determined from the boundary conditions at the rope ends and at point P:

boundary condition	equation
Height of the bearing on the left:	${\displaystyle y_{1}(0)=y_{0}}$
Right bearing height:	${\displaystyle y_{2}(L_{2})=y_{L}}$
Sag in P:	${\displaystyle y_{1}(L_{1})=y_{2}(0)}$
Horizontal equilibrium of forces in P:	${\displaystyle H_{1}-F_{x}=H_{2}}$
Vertical equilibrium of forces in P:	${\displaystyle H_{1}y_{1}'(L_{1})+F_{y}=H_{2}y_{2}'(0)}$
Rope length:	${\displaystyle \textstyle l=\int _{0}^{L_{1}}{\sqrt {1+y_{1}'^{2}}}\,\mathrm {d} x_{1}+\int _{0}^{L_{2}}{\sqrt {1+y_{2}'^{2}}}\,\mathrm {d} x_{2}}$

example

Profile of the Schwägalp – Säntis cable car. The straight lines connecting the suspension points are dashed, the rope lines are solid and the rope line in the first section, which results without the cabin, is shown dotted.

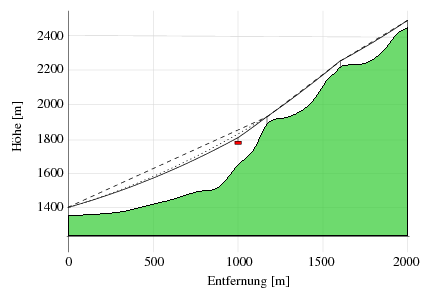
The Schwägalp – Säntis cable car leads from Schwägalp to the mountain station on the Säntis , see picture. Technical data and precise topographic maps are available on the Internet. The data of the cable car are compiled in the table.

size	value	unit
Weight of the suspension ropes	12.3	kg / m
Breaking strength of the suspension ropes	2350	kN
Suspension cable tension weight per lane	98,000	kg
Gross weight of the cabin	15,890	kg
Location of the valley station (x, y)	(0, 1351)	m
Location of the first column (x, y)	(1170, 1900)	m
Location of the second column (x, y)	(1600, 2250)	m
Location of the mountain station (x, y)	(2009, 2473)	m

It should be clarified to what extent the breaking force of the ropes is exhausted when the vertically hanging cabin has traveled 1000 m in the horizontal direction, i.e. just before the first support as shown in the picture. Friction losses should be negligible.

Because all forces act in the vertical direction, the horizontal pull is constant throughout the rope. Two suspension ropes are tensioned per carriageway so that the tensioning and cabin weights are distributed over two ropes. The gravitational acceleration of 9.81 m / s² results in the rope force S ₀ in the valley station, the individual force F and the line load

${\displaystyle {\begin{aligned}S_{0}=&{\frac {98{.}000\,{\rm {kg}}}{2}}\cdot 9{,}81{\frac {\rm {m}}{\rm {s^{2}}}}=481\,{\rm {kN}}\\F=&{\frac {15{.}890\,{\rm {kg}}}{2}}\cdot 9{,}81{\frac {\rm {m}}{\rm {s^{2}}}}=78\,{\rm {kN}}\\q_{0}=&12{,}3{\frac {\rm {kg}}{\rm {m}}}\cdot 9{,}81{\frac {\rm {m}}{\rm {s^{2}}}}=121\,{\frac {\rm {N}}{\rm {m}}}\end{aligned}}}$

The unknowns in the rope lines worked out in the previous section are here

Site plan of the rope and free body picture in point P

specification	equation
Height of the camp on the left	y 1 (0) = 1351 m
Rope force in the left bearing	${\displaystyle H{\sqrt {1+y_{1}'(0)^{2}}}=S_{0}}$
Place P of the individual force	L 1 = 1000 m
Distance from P to the right bearing	L 2 = 170 m
Right bearing height	y 2 ( L 2 ) = 1900 m
Slack in P	y 1 ( L 1 ) = y 2 (0)
Vertical equilibrium of forces in P	H y 2 '(0) = H y 1 ' ( L 1 ) + F

The rope length is not required. Because only a slight sag is observed, the weight force is assumed to be a constant line load, so that the rope lines in front of and behind the cabin

${\displaystyle y_{1}(x_{1})={\frac {q_{0}}{2H}}x_{1}^{2}+C_{1}x_{1}+C_{0}\quad {\text{und}}\quad y_{2}(x_{2})={\frac {q_{0}}{2H}}x_{2}^{2}+C_{3}x_{2}+C_{2}}$

be valid. The five equations in the table are available for determining the unknowns C _0,1,2,3 :

${\displaystyle {\begin{aligned}y_{1}(0)=&C_{0}=y_{0}\\y_{2}(L_{2})=&{\frac {q_{0}}{2H}}L_{2}^{2}+C_{3}L_{2}+C_{2}=y_{L}\\y_{1}(L_{1})=&{\frac {q_{0}}{2H}}L_{1}^{2}+C_{1}L_{1}+C_{0}=y_{2}(0)=C_{2}\\S_{0}=&H{\sqrt {1+C_{1}^{2}}}\\HC_{3}=&H\left({\frac {q_{0}}{H}}L_{1}+C_{1}\right)+F\end{aligned}}}$

This system of equations has the solution:

${\displaystyle {\begin{aligned}C_{0}=&y_{0}=1351\,{\rm {m}}\\C_{1}=&p-{\sqrt {p^{2}-q}}=0{,}2917\\H=&{\frac {S_{0}}{\sqrt {1+C1^{2}}}}=461\,{\rm {kN}}\\C_{2}=&{\frac {q_{0}L_{1}^{2}}{2H}}+L_{1}C_{1}+y_{0}=1773\,{\rm {m}}\\C_{3}=&{\frac {q_{0}}{H}}L_{1}+C_{1}+{\frac {F}{H}}=0{,}7221\end{aligned}}}$

With

${\displaystyle {\begin{aligned}L=&L_{1}+L_{2},\quad M={\frac {q_{0}}{2}}L^{2}+FL_{2},\\p=&{\frac {S_{0}^{2}y_{L}L}{S_{0}^{2}L^{2}-M^{2}}}\quad {\text{und}}\quad q={\frac {S_{0}^{2}y_{L}^{2}-M^{2}}{S_{0}^{2}L^{2}-M^{2}}}.\end{aligned}}}$

The vertical pulls are calculated at the location of the cabin

${\displaystyle {\begin{aligned}V_{1}(L_{1})=&q_{0}L_{1}+C_{1}H=255\,{\rm {kN}}\quad (261\,{\rm {kN}})\\V_{2}(0)=&HC_{3}=333\,{\rm {kN}}\quad (339\,{\rm {kN}})\end{aligned}}}$

and the rope forces

${\displaystyle {\begin{aligned}S_{1}(L_{1})=&{\sqrt {H^{2}+V_{1}^{2}(L_{1})}}=527\,{\rm {kN}}\quad (531\,{\rm {kN}})\\S_{2}(0)=&{\sqrt {H^{2}+V_{2}^{2}(0)}}=569\,{\rm {kN}}\quad (574\,{\rm {kN}})\end{aligned}}}$

Only about a quarter of the breaking force of 2350 kN is used in P. The rope forces calculated with the chain line are shown in brackets. They are all higher than those calculated here, but the deviation is less than 3%.

Individual evidence

1. ↑ Dankert (2009), p. 157ff.
2. ↑ Schwägalp-Säntis cable car. (PDF) Technical description. Säntis-Schwebebahn AG, January 2016, accessed on December 28, 2016 . 
3. ↑ Topographic map of the route. Federal Office of Topography swisstopo, accessed on December 28, 2016 . 

literature

• Jürgen Dankert, Helga Dankert: Technical Mechanics . Statics, strength theory, kinematics / kinetics. 5th edition. Vieweg + Teubner, 2009, ISBN 978-3-8351-0177-7 , pp. 157 ff . ( google.de ).