Balance (clock)

Balance is the abbreviation for a balance-spring oscillation system as used in mechanical watch movements. The oscillation system serves as a regulator for small watches , i.e. especially for wristwatches and pocket watches , but also for alarm clocks, wall clocks, chronometers, etc. The precursor of the balance was the Unrest .
The balance wheel oscillates around its axis with a certain period of oscillation or frequency , which is determined by the two pivots (see picture). In conjunction with the escapement , it ensures the alternating, step-by-step stopping and releasing of the gear train (drive), which is driven by the clock's energy source (spring drive, see barrel ) (see also clockwork ). The step-by-step process (and thus the passage of time) is indicated by a pointer train connected to the gear train .
The idea of using the balance wheel together with a spiral spring was developed by Christiaan Huygens on a proposal by Jean de Hautefeuille , and in 1675 he was granted a French patent for it.
precursor
Until the invention of suitable escapement systems, only the pendulum clock had a satisfactory accuracy, but could not be transported without damage. The portable clocks developed for the first time in the 15th century (see Nuremberg Egg ), on the other hand, were equipped with short torsion pendulums for reasons of space . However, these were influenced by every movement of the wearer and had daily errors of up to several minutes. The invention of the torsion pendulum as a clock generator for portable clocks was wrongly attributed to Peter Henlein , but was known as early as the early 15th century. The oldest wearable clock comes from Henlein .
construction
The oscillating system consists of the actual balance wheel (balance shaft with trumpet pivot, double roller with lever stone, balance ring, balance arm) and the hairspring (with spiral studs and spiral roller). The materials used are steel, spring steel, spring bronze, brass, but especially special alloys that should be as non-magnetic as possible (influence of external magnetic fields). In the last handle of the hairspring, two so-called regulator pins (regulator keys) engage, which are attached to an arm that can be rotated on the balance cock. They are used to regulate the period of oscillation (see below).
The balance is stored in two (oiled) bearings, each consisting of perforated and cap stones, which are located in the balance cock or the plate. In good works, the journal bearings are made of corundum , previously made of natural sapphires and rubies, today made of synthetically produced ones in order to enable the lowest possible friction. The balance pins have a very small diameter. This ensures that the pin friction when the pin is in contact with the hole stone (frictional torque when the balance shaft is not in a vertical position) is low and does not differ significantly from the friction conditions with a vertical balance shaft (point contact of the spherical pin with the cap stone). This minimizes the difference in time between different positions of the (portable) clocks. The low journal friction also ensures that the oscillation is only weakly dampened and thus the energy (periodically supplied by the escapement) to maintain the oscillation is reduced (power reserve ). The disadvantage of the filigree tenons is the risk of breakage if the watch is hit. The trumpet-like cone shape counteracts this, but does not completely eliminate the danger. So that the journals are not damaged in the event of impact , a shock protection device is used , such as B. Parechoc or Incabloc . The jewels are movably supported by a spring and can avoid impacts. So-called grain bearings are common for simple clocks (conical journal in a conical bearing socket). Special bearings (e.g. magnetically relieved) are also known.
The (Archimedean) spiral is preformed and therefore has a tension-free central position. It should have at least ten turns. The spiral is attached to the inside of the spiral roller, which is (detachably) connected to the balance shaft. The outer end is pinned in the spiral block which is held in the balance cock or the balance bridge. The lever stone (also known as an ellipse, usually made of ruby) is located on the double roller (double disc). Via this, on the one hand, the oscillation system receives the drive impulses required to maintain the oscillation, and on the other hand, it switches the escapement in time with the balance oscillation. This applies to the lever escapement, which is predominantly used in portable watches . With further escapements ( spindle escapement , cylinder escapement , chronometer escapement , coaxial escapement or co-axial escapement, etc.), these two tasks are implemented in a different way.
Period of oscillation
The balance represents an inert mass (centrifugal mass, moment of inertia). If it is deflected from the central position determined by the tension-free spiral, a restoring force (more precisely: a torque) arises from the tension-free spiral Vibration. If the torque curve is linear (proportional) as a function of the deflection angle, the oscillation system oscillates harmoniously (friction neglected). In this case, oscillations with small and large amplitudes have the same oscillation duration ( isochronism ). This is a desirable state, because the oscillating system cannot be supplied with constant large drive pulses due to the drop in torque of the mainspring (energy storage) that drives the watch. This would have no effect on the accuracy of the clock if isochronism could be implemented, which is only possible approximately. Attempts have also been made to keep the drive pulses constant despite the torque drop in the drive spring (see intermediate lift ). The oscillation system then oscillates constantly with the same oscillation amplitude and the isochronism error (i.e. the non-linearity) does not matter.
The period of the balance oscillation depends on the moment of inertia of the balance and on the directional moment of its spiral:
The balance's moment of inertia is determined by its design and the materials used. For an estimate it is sufficient to only consider the balance ring (see picture). The real value of the moment of inertia is then somewhat larger. The balance wheel vibrates at a slightly lower frequency than calculated. Under this condition:
The mass of the ring is calculated as follows:
is the density of the material used (for brass and Glucydur approx. ).
The directional moment for a spiral with a rectangular blade cross-section ( area moment of inertia , width , height , active length , modulus of elasticity ) results from
- (see image)
The modulus of elasticity is z. B. with Nivarox spirals approx and with Elinvar spirals approx . The spiral length can be calculated with a good approximation if you use the mean radius of the full turns and add the remaining piece up to the regulator (see picture). The equation then reads:
When calculating the spiral length exactly (see spiral or), it must be ensured that the corresponding formula applies to the spiral beginning at the zero point. So you also have to calculate the length li from the zero point to the spiral roller and subtract it from the total length determined (see attached picture).
The equations assume that the spiral remains in its linear working range and the damping can be neglected. A (reciprocal) measure of damping is the quality factor - a quality feature of the movement. A low quality means that a considerable part of the contained energy has to be supplied by the escapement per period . This makes the clock sensitive to changes in the spring tension of the mainspring . On the other hand, a high quality also reduces the influence of periodic disturbances, for example when the person wearing the watch waves or applauds.
The usual oscillation frequency is 18,000 vibrations per hour. Produced in series Quick chair work with up to 36,000 vibrations per hour, with serial works but usually 21,600 or 28,800 balance vibrations are spread per hour.
In principle, the higher the frequency, the less such interference. Therefore, the introduction of the fast- swinging balance brought about a noticeable improvement in the rate of the watch . The largest possible oscillation amplitude (standard min. 220 ° per half oscillation) also contributes to the fact that disturbances (e.g. due to the inhibition) have less of an impact, as the kinetic energy of the oscillation system in the area of its central position (where the inhibition intervenes with the Energy supply) is then greater in relation to the disturbance.
Problems and solutions
Balance
Since the period of oscillation essentially depends on the moment of inertia of the balance wheel and the properties of the hairspring, changes in temperature due to dimensional changes and changes in the material properties (elasticity module of the hairspring) affect the accuracy. Compensation balance was therefore developed from a cut bimetal ring (mostly made of steel combined with brass). Compensation balance (also called bimetal balance) has adjusting screws on the balance ring (see compensation ). The disadvantage was that the compensation is not the same at every temperature and only at two temperatures there is no temperature-related rate deviation. Thanks to the use of special temperature-stable alloys (Elinvar, Nivarox, etc.) for spiral springs, the need for compensation has been eliminated since the 1930s, so that since around 1960, only monometallic balance balances (mostly made of brass) have been increasingly used.
In the case of portable watches, the oscillating system changes its position. An eccentric center of gravity of the balance wheel acts like a small pendulum depending on the position of the clock and causes (except when the balance shaft is exactly vertical) rate deviations in the clock. It is therefore necessary that the balance wheel is balanced. This means the exact shift of the center of gravity to the axis of the balance shaft. In the past, this was done by (multiple) manual removal of material on the balance ring or (similar to the compensation balance) by adjusting screws on the balance ring (screw balance). The control was carried out with a balance balance. These were activities that involved a lot of work. In modern watch production, the balance is balanced by machine with a single milling process. Screw balances are still being made. However, the screws are only decorative and are not functionally required.
spiral
Flat spirals are built into portable watches. In stationary watches (especially chronometers), helical springs (helix) are used (see video).
With the materials previously used for the spiral, the change in the modulus of elasticity with a change in temperature played a major role. Compensation unrest was therefore necessary for precise clocks. Modern spirals consist of special alloys that are practically no longer temperature dependent (recently also silicon materials).
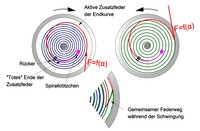
The above-mentioned desirable linear characteristic for the return torque M (α) of the spiral would be given if, with any rotation of the balance shaft by α and a force F (α) acting on the outer spiral end, there would be a uniform change in curvature of the entire spiral (compared to the curvature the tension-free middle layer).
The spiral would then oscillate concentrically (“breathe”). For this, however, the line of action of the force would have to shift continuously during the oscillation (e.g. from P to P *, see figure) and thus the radius r (α) would have to change. However, the spiral is fixed on the outside at a fixed point P by the spiral block. The consequence of this is that a uniform change in curvature is not possible (as shown exaggerated in the picture for clarity) and consequently the return torque has a non-linear characteristic curve (no isochronism). Furthermore, the center of gravity of the hairspring, which is not on the axis of the balance shaft even in the central position, is shifted during the oscillation. The eccentric center of gravity of the spiral has a similar effect on the clock rate as the eccentric center of gravity of the balance, as it is also influenced by gravity.
For watches with normal requirements, the rate deviation caused by the non-linearity of the returning torque is tolerable if the spiral has ten or more turns, because then the deviation from the ideal change in curvature is not too great (illustrated in the picture for a half oscillation of 180 °).
However, this is not the case for precise watches.
Breguet spiral (movement)
Breguet has experimentally found a way to achieve an approximately linear characteristic. Put simply, he provided the spiral with an additional spring (see picture). This must be shaped so that
- it exerts a force F (α) on the spiral which, at any angle of rotation α, corresponds exactly to the force required for a uniform change in the curvature of the spiral;
- the line of action of the force shifts when the balance shaft is rotated by α exactly as required by the uniform change in curvature;
- the line of action is always tangential to the spiral end.
The spring end of the additional spring then represents a movable spiral block, as it were, and when deflected, moves on the same spring path as the end of the oscillating spiral when its curvature changes evenly.
Breguet has expediently implemented the additional spring by extending the spiral and shaping this extension accordingly (end curve). To do this, he had to raise the end curve to a level above the spiral, otherwise the spiral and the additional spring would collide. Two kinks are to be made for this (see picture). Continuous twisting is also possible. The Breguet hairspring is difficult to manufacture by hand. End curves for the inner end of the spiral are also known, but are not used. Helical springs are also provided with end curves.
Long after Breguet, Phillips treated the end curve problem theoretically. As a result, he established three simple rules:
- The end curve must be tangential to the end of the spiral
- The center of gravity of the end curve must lie on a perpendicular to a line going through the center point to a line from the spiral center point to the spiral end
- The product of the center of gravity distance from the center point and the spiral length must be equal to the square of the distance between the spiral end and the center point
The rules apply to the voltage-free state (central position). According to these rules, end curves were designed as templates (Gerstenberger), according to which the watchmakers could shape the spirals. The theoretical curves are slightly modified based on practical experience. Due to the Phillips curves, the center of gravity of the scroll is also shifted to the axis of the balance shaft and remains there during the oscillation.
With modern silicon spirals, similar results can be achieved even without end curves. Using the appropriate manufacturing methods (lasers, etching, etc.), such spirals can be manufactured with a cross-section that can be changed over their length, which opens up completely new design options
Rücker
The regulator is a simple way of setting the oscillation period of the oscillation system. Otherwise the length of the spiral would have to be adapted to the requirements by laboriously pinning and pinning. By moving the regulator, the effective (or also active) spiral length and thus the period of oscillation is changed. This length extends from the spiral roll to the regulator. The area from the regulator to the block is the "dead" end of the spiral, which has (approximately) no influence on the period of oscillation. The spiral swings between the two regulator pins and alternately rests against them. This means that different effective spiral lengths are effective during an oscillation. When the regulator pins are touched, the length is shortened. This makes it clear that the regulator offers a simple possibility of regulation, but on the other hand there is an undefined source of interference (e.g. with large oscillation amplitudes, the spiral is longer on the regulator pins than with small ones). The desired isochronism is thereby disturbed. This also applies to Breguet spirals, where the regulator acts on the end curve (additional spring).
compensation
Caspari and Grossmann have developed ways in which spirals without end curves can be used and still an approximately even rate of the clock can be achieved with large and small oscillation ranges. For this purpose, opposing interfering influences are used to compensate for each other's effects. For example, the play of the spiral in the regulator key causes the clock to slow down in the case of small oscillation amplitudes, while a certain structurally determined position of the inner and outer fastening point of the spiral to each other results in a procedure in this case. For details see.
High-quality modern mechanical watches are made with flat caspari and Grossmann spirals as well as with Breguet spirals (Phillips end curves).
Reglage
As a regulator is called the fine adjustment of a clock.
The watchmaker uses a timing machine to check the regulation and thus the accuracy , a device in which the vibration is measured and graphically displayed with a structure-borne sound microphone . A Micro-Dynagraph can be used to record the fluctuations in the moment of force on the escape wheel , the change in the oscillation amplitude of the balance wheel and the rate deviations of the watch.
literature
- Otto Böckle, Wilhelm Brauns: Textbook for the watchmaking trade. Work skills and materials. 8-10 Edition. Wilhelm Knapp, Halle (Saale) 1951, (reprint, edited by Michael Stern. Heel, Königswinter 2010, ISBN 978-3-86852-288-4 ).
- Hermann Brinkmann: Introduction to watchmaking (= The watchmaking school. Vol. 2). 10th unchanged edition. Wilhelm Knapp, Düsseldorf 2005, ISBN 3-87420-010-8 .
- George Daniels : Watchmaking. Updated 2011 edition. Philip Wilson Publishers, London 2011, ISBN 978-0-85667-704-5 .
- Helmut Kahlert , Richard Mühe , Gisbert L. Brunner : Wristwatches: 100 years of development history. Callwey, Munich 1983; 5th edition, ibid 1996, ISBN 3-7667-1241-1 , pp. 36-59.
Web links
Individual evidence
- ↑ Milham, Willis I. (1945). Time and timekeepers. New York: MacMillan. ISBN 0-7808-0008-7 ., P.121
- ↑ "Clock". The New Encyclopaedia Britannica. 4. Univ. of Chicago. 1974. p. 747. ISBN 0-85229-290-2 .
- ↑ Anzovin, Steve; Podell, Janet (2000). Famous First Facts: A record of first happenings, discoveries, and inventions in world history. HW Wilson Company. ISBN 0-8242-0958-3 ., P.440
- ↑ Usher, Abbot Payson (1988). A History of Mechanical Inventions. Courier Dover. ISBN 0-486-25593-X ., P.305
- ^ White, Lynn Jr. (1966). Medieval Technology and Social Change. New York: Oxford Univ. Press. ISBN 0-19-500266-0 ., P. 126-127
- ^ Dohrn-van Rossum, Gerhard (1997). History of the Hour: Clocks and Modern Temporal Orders. Univ. of Chicago Press. ISBN 0-226-15510-2 ., P.121
- ↑ Krug u. a .: BI Lexicon Clocks and Time Measurement . Ed .: Rudi Koch.
- ^ Siegfried Hildebrand: Feinmechanische Bauelemente. VEB Verlag Technik Berlin
- ^ Siegfried Groß: Calculation and design of springs. Jumper
- ↑ Geometry: Archimedes Spiral Calculator - Calculatoronline. Retrieved May 2, 2017 .
- ^ Helmut Kahlert , Richard Mühe , Gisbert L. Brunner , Christian Pfeiffer-Belli: wrist watches: 100 years of development history. Callwey, Munich 1983; 5th edition, ibid 1996, ISBN 3-7667-1241-1 , p. 505.
- ^ Helmut Kahlert , Richard Mühe , Gisbert L. Brunner : Wristwatches: 100 years of development history. Callwey, Munich 1983; 5th edition ibid. 1996, ISBN 3-7667-1241-1 , pp. 36-39.
- ↑ c9w3W9m1: balance wheel of a clock in action. March 27, 2010, accessed October 3, 2017 .
- ^ Edouard Phillips: Mémoire sur le spiral réglant des chronomètres et des montres. 1860, accessed April 1, 2017 (French).
- ↑ Phillips end curves. Retrieved April 16, 2017 .
- ↑ Oscillating system for mechanical clockworks. Retrieved April 16, 2017 .
- ↑ DEPATISnet | Document CH000000703272A2. Retrieved May 2, 2017 .
- ↑ DEPATISnet | Document CH000000699882A2. Retrieved May 2, 2017 .
- ↑ Martinek Rehor: Mechanical watches. VEB Verlag Technik Berlin