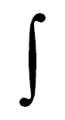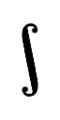Integral sign

∫
Mathematical signs
arithmetic
Plus sign	+
Minus sign	- , ./.
Mark	⋅ , ×
Divided sign	: , ÷ , /
Plus minus sign	± , ∓
Comparison sign	< , ≤ , = , ≥ , >
Root sign	√
Percent sign	%
Analysis
Sum symbol	Σ
Product mark	Π
Difference sign , Nabla	∆ , ∇
Prime	′
Partial differential	∂
Integral sign	∫
Concatenation characters	∘
Infinity symbol	∞
geometry
Angle sign	∠ , ∡ , ∢ , ∟
Vertical , parallel	⊥ , ∥
Triangle , square	△ , □
Diameter sign	⌀
Set theory
Union , cut	∪ , ∩
Difference , complement	∖ , ∁
Element character	∈
Subset , superset	⊂ , ⊆ , ⊇ , ⊃
Empty set	∅
logic
Follow arrow	⇒ , ⇔ , ⇐
Universal quantifier	∀
Existential quantifier	∃
Conjunction , disjunction	∧ , ∨
Negation sign	¬

The integral sign is derived from the letter s ("ſ") as an abbreviation for the word sum , Latin ſumma . This symbolic notation of integrals goes back to Gottfried Wilhelm Leibniz . For the integral sign there are a number of variations, including for multiple integrals , line integrals , surface integrals and volume integrals . ${\displaystyle \textstyle \int }$

history

Leibniz first mentioned the integral sign in a later published manuscript Analysis tetragonistica of October 29, 1675.

" Utile erit scripsisse ∫ pro omnia "

"It will be useful to write ∫ instead of omnia"

Omnia stands for omnia l and is used in the geometrically oriented area calculationmethodby Bonaventura Cavalieri . Leibniz's corresponding printed publication is De geometria recondita ( Latin for “The geometry is saved”), from 1686. At that time he called the integral calculus calculus summatorius , hence the long S. Johann I Bernoulli was also busy at the time with the topic, and since Leibniz was striving for uniform scientific symbols, they discussed it. So the sign of Leibniz and the name calculus integralis , integral calculus, remained from Bernoulli.

use

The integral of a real function with respect to the variable over the interval is given by ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle [a,b]}$

${\displaystyle \int \limits _{a}^{b}f(x)\;\mathrm {d} x}$

written down. The multiplicative notation indicates how the integral operation from strips of height and infinitesimal width adds up to the area under the function. ${\displaystyle f(x)\;\mathrm {d} x}$ ${\displaystyle f(x)}$ ${\displaystyle \mathrm {d} x}$

Traditions of the formula set

Slightly different forms of the integral sign have become established in the various traditions of the formula set . In the German formula set, the form shown in the picture German form of the integral sign is used, while, for example, in the Russian area a form variant has been established that reproduces the graphic Russian form variant of the integral sign.

• 

  German form of the integral sign

• 

  Russian variant of the integral sign

In addition, in American typesetting, the upper and lower limits are placed to the right of the integral sign in text formulas in order to limit disruptive line spacing.

${\displaystyle \int _{0}^{T}f(t)\;\mathrm {d} t,}$

while in German tradition

${\displaystyle \int \limits _{0}^{T}f(t)\;\mathrm {d} t}$

is common. Integrals in text formulas are always smaller than in separate formulas.

Coding

The integral symbol and its modifications are encoded in computer systems as follows.

Coding in Unicode, HTML and LaTeX

character	Unicode		designation	HTML			Latex
	position	designation		hexadecimal	decimal	named
∫	U+222B	integral	integral	& # x222B;	& # 8747;	& int;	\int
∬	U+222C	double integral	Double integral	& # x222C;	& # 8748;		\iint
∭	U+222D	triple integral	Triple integral	& # x222D;	& # 8749;		\iiint
∮	U+222E	contour integral	Curve integral	& # x222E;	& # 8750;		\oint
∯	U+222F	surface integral	Surface integral	& # x222F;	& # 8751;		\oiint
∰	U+2230	volume integral	Volume integral	& # x2230;	& # 8752;		\oiiint
∱	U+2231	clockwise integral	clockwise integral	& # x2231;	& # 8753;		\intclockwise
∲	U+2232	clockwise contour integral	clockwise curve integral	& # x2232;	& # 8754;		\ointclockwise
∳	U+2233	anticlockwise contour integral	counter-clockwise curve integral	& # x2233;	& # 8755;		\ointctrclockwise
⌠	U+2320	top half integral	upper half of an integral	& # x2320;	& # 8992;
⌡	U+2321	bottom half integral	lower half of an integral	& # x2321;	& # 8993;
⎮	U+23AE	integral extension	Extension of an integral	& # x23AE;	& # 9134;
⨋	U+2A0B	summation with integral	Integral sum	& # x2A0B;	& # 10763;		\sumint
⨌	U+2A0C	quadruple integral operator	Quadruple integral	& # x2A0C;	& # 10764;		\iiiint
⨍	U+2A0D	finite part integral	Integral with finite part	& # x2A0D;	& # 10765;		\dashint
⨎	U+2A0E	integral with double stroke	Integral with double line	& # x2A0E;	& # 10766;		\ddashint
⨏	U+2A0F	integral average with slash	Mean value integral with dash	& # x2A0F;	& # 10767;		\strokedint
⨑	U+2A11	anticlockwise integration	counterclockwise integral	& # x2A11;	& # 10769;		\intctrclockwise
⨕	U+2A15	integral around a point operator	Integral around a point	& # x2A15;	& # 10773;
⨖	U+2A16	quaternion integral operator	Quaternion integral	& # x2A16;	& # 10774;		\sqint
⨗	U+2A17	integral with leftwards arrow with hook	Integral with left arrow with hook	& # x2A17;	& # 10775;
⨘	U+2A18	integral with times sign	Integral with marks	& # x2A18;	& # 10776;
⨙	U+2A19	integral with intersection	Integral with average	& # x2A19;	& # 10777;		\landdownint
⨚	U+2A1A	integral with union	Integral with union	& # x2A1A;	& # 10778;		\landupint
⨛	U+2A1B	integral with overbar	Integral with overline	& # x2A1B;	& # 10779;
⨜	U+2A1C	integral with underbar	Integral with underscore	& # x2A1C;	& # 10780;

Web links

Commons : Mathematical integration symbols  - collection of images, videos and audio files

Wiktionary: integral signs  - explanations of meanings, word origins, synonyms, translations

Individual evidence

1. ^ Carl von Prantl:  Leibniz, Gottfried Wilhelm . In: Allgemeine Deutsche Biographie (ADB). Volume 18, Duncker & Humblot, Leipzig 1883, pp. 172-209., Search calculus summatorius
2. ^ Alfred Warner, Historical Dictionary of Electrical Engineering, Information Technology and Electrophysics
3. ↑ Zaitcev, V .; Janishewsky, A .; Berdnikov, A. (1999), Russian Typographical Traditions in Mathematical Literature. EuroTeX'99 Proceedings ( Online ( Memento of the original from September 28, 2012 in the Internet Archive ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this note .; PDF; 200 kB ) 
4. ↑ Scott Pakin: The Comprehensive LaTeX Symbol List. (PDF, 8.7 MB) January 19, 2017, archived from the original on September 28, 2017 ; Retrieved on September 28, 2017 (English, linking the original results in a mirror of CTAN , the archive link compare file: Comprehensive LaTeX Symbol list.pdf ).