Larmor precession
Larmor precession (after the Irish physicist Joseph Larmor ) is the precession of the angular momentum of a particle with a magnetic dipole moment around the direction of an external magnetic field . In the case of atoms , it can be observed in particular through the splitting of spectral lines caused by the magnetic field , the Zeeman effect .
The frequency of the precession movement is called the Larmor frequency . In the case of a charged particle, the Larmor frequency differs from the cyclotron frequency in the same magnetic field by half the Landé factor . This can be explained quantum mechanically .
Important applications of the Larmor precession are magnetic resonance spectroscopy and magnetic resonance tomography .
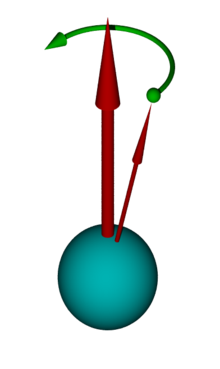
Precession using the example of the heavy top
On a gyro that is not stored in its center of gravity and whose axis of rotation is not perpendicular - z. B. a toy top - gravity acts with a torque that is perpendicular to gravity and the axis of the top. If the top doesn't turn, it will fall over. In the case of (not too slow) rotation, on the other hand, the torque causes a precession movement that guides the top axis and thus the angular momentum vector in a circle around the perpendicular. The angle of attack to the perpendicular remains constant and the angular velocity of the precession is the same for all angles of attack.
Precession in a magnetic field
The Larmor precession is based on the fact that every charged particle with angular momentum also represents a magnetic dipole . This also applies to totally neutral particles (e.g. neutrons , neutral atoms with an odd number of electrons), which are composed of charged particles whose magnetic moments do not add up to zero. In a magnetic field a torque acts on the particle , which tends to make the dipole parallel to the field direction. It is . Magnitude and direction of the dipole are given by the angular momentum vector: . Here the gyromagnetic ratio is a constant that can be calculated for each energy level according to the Landé formula, depending on the type of particle. The precession with the Larmor frequency follows from the equation of motion of the top,, . This is proportional to and to the flux density of the magnetic field
or as angular frequency (with the Landé factor , the charge and the mass of the particle)
Macroscopic effect
The above description applies equally to classical and quantum physics. Has one z. For example, if a drop of water is slightly magnetized by a strong magnetic field, the (partially) aligned magnetic moments of the protons ( atomic nuclei of hydrogen ) together form a weak macroscopic dipole magnet, which is connected to a small total angular momentum via the same gyromagnetic factor. If the magnetic field is replaced quickly enough by one in a different direction, this dipole magnet will retain its original orientation for a short time and will perform the Larmor precession. It generates an easily observable induced alternating voltage in an antenna coil , the frequency of which is the Larmor frequency. The amplitude of the alternating voltage decreases as the strength of the rotating dipole perpendicular to the field direction decreases because the macroscopic magnetization adapts to the new field direction (longitudinal relaxation ) and because the individual protons get out of step due to small disturbances (transverse relaxation). Both the precise measurement of the frequency and the observation of the relaxation are among the most important tools in materials research when researching structures and reactions. In geophysics, this procedure is used in the proton magnetometer to precisely measure the earth's magnetic field and its disturbances.
Quantum mechanical description
Zeeman effect
In terms of quantum mechanics, the magnetic moment in the magnetic field splits up the energy level with the angular momentum quantum number into equidistant levels to the various possible magnetic quantum numbers . The level distance is always (therein is the reduced quantum of action ). This splitting was first observed in 1896 on optical spectral lines and was one of the first approaches to studying the processes in atoms and thus to the development of quantum mechanics.
In formulas: The above torque shows that the particle in the magnetic field has additional energy
where is the component of the vector that is too parallel and the field direction was chosen as the z-axis. Since the quantum numbers belong to (see directional quantization ), the level splits into as many Zeeman levels . Your energies are
Precession movement
According to quantum mechanics, no movement can be read from a single Zeeman state, neither the rotation around the top axis nor the precession of the top axis around the axis. As an eigenstate of an energy , the state is stationary, i.e. H. with advancing time, its shape does not change, only the quantum mechanical phase of its state vector by means of the phase factor . States of different energies change their phase at different speeds. In the case of the Zeeman states with energy split according to the magnetic quantum number , the phase factor is accordingly . Since it is precisely the eigenvalue of the component of the angular momentum of the Zeeman state in question, this phase factor means the same as a rotation around the angle around the z-axis. For a Zeeman state alone, this phase or rotation is not expressed in any observable fact, only in the phase factor of the associated state vector, which is in principle arbitrary according to quantum mechanics.
A rotational movement around the -axis can only be observed in a state that at any given moment characterizes a certain direction perpendicular to the -axis in a measurable way. To do this, it must be a superposition of several Zeeman states. Which axis is marked perpendicular to the axis then depends on the relative phase of its Zeeman components. For example, a particle with spin can have the Zeeman states and , and the state aligned to the -axis is given by the superposition (apart from a common factor, see also properties of spin ). If the phases of the two components have developed 90 ° apart for whatever reason, the state is called (apart from one common factor) and has aligned the spin towards the -axis. After another 90 ° phase difference, the state is called and is aligned, etc.
Since the individual state vectors change with the passage of time, as if they had all been rotated by the same angle around the axis, the same superposition now describes a state that has actually performed this rotation. If at the beginning it showed a polarization that was not parallel to the -axis, then later it shows the same shape and strength of the polarization, but in a correspondingly rotated direction.
In other words: the system described rotates entirely with angular velocity , in complete agreement with the view. Here it becomes clear that the energy splitting of the angular momentum eigenstates as in the Zeeman effect allows such a simple spatial illustration, because it is equidistant. A split proportional to the square of the magnetic quantum number, such as B. through the interaction of the electric quadrupole moment with an inhomogeneous electric field, cannot be interpreted in this way.
Effect on polarized particle beams
The Larmor precession can become noticeable when working with a spin-polarized ion beam if the beam crosses matter - such as a foil or a gas. If an ion traps an electron, the spin vector of this ion then precesses around the (random) direction of the electron's much larger magnetic moment, so that the polarization of the beam is reduced.
In the case of a film behind which there is a vacuum, the captured electron can remain permanently bound; then, after a period of precession, all ion spins have their original directions again, and the polarization has returned to the initial value. If the speed of the ions corresponds to an easily measurable distance per Larmor orbit, a sinusoidal decreasing and increasing polarization can be measured along the beam path. This was clearly demonstrated in an experiment with polarized deuterons of around 160 keV .
Magnetic resonance
By irradiating an alternating magnetic field, transitions between the levels split in the Zeeman effect are stimulated if the frequency of the alternating field matches the Larmor frequency ( resonance ). By varying the frequency, an absorption spectrum with a visible absorption line is created. This method is called electron spin resonance or nuclear magnetic resonance , depending on the object being observed, and allows measurements with extreme accuracy. For example, with nuclear magnetic resonance, the influence of the chemical bond between the atom and its wider environment can be measured because it changes the magnetic field acting on the nucleus by a fraction of a million ( chemical shift ).
This absorption of energy can also be understood macroscopically, because a linearly polarized alternating field contains a circularly polarized component that exerts a constant moment (in its rest system) on the precessing dipole at the correct frequency. If it is heading “as if it wanted to accelerate precession”, energy is supplied to the top. But it cannot store this in the form of a faster precession, because the Larmor frequency is fixed. Instead, the gyroscope absorbs the energy - in the classic vivid way - by increasing the setting angle (away from the constant field ), expressed in quantum mechanics by a correspondingly increasing admixture of Zeeman states with a lower m-quantum number. On a large toy top that precesses in a gravitational field, you can directly observe the classic behavior when you try to accelerate (or slow down) the precession with your finger.
Web links
literature
- Gerthsen, Kneser, Vogel: Physics . 13th edition, Springer 1977, ISBN 978-3-662-09311-5 , page 478
- W. Zinth, H.-J. Grains: optics, quantum phenomena and the structure of atoms. Oldenbourg Verlag 1998, ISBN 3-486-24054-4 , page 256
- 13C-NMR spectroscopy , H.-O. Kalinowski, S. Berger, S. Braun; Georg Thieme Publishing House
- 13C-NMR spectroscopy , E. Breitmaier, G. Braun; Georg Thieme Verlag (an exercise book)
Individual evidence
- ↑ WW Lindstrom, R. Garrett, U. von Möllendorff: Depolarization of low-energy deuterons by electron pick-up. Nuclear Instruments and Methods Volume 93 (1971) p. 385