Heat transfer coefficient
The heat transfer coefficient is a measure of the heat transfer through a solid body (such as a wall) from one fluid (a gas or a liquid) into a second fluid due to a temperature difference between the fluids. In the case of a flat wall, it indicates the heat flow (heat energy per time) per area of the wall and per Kelvin temperature difference between the two fluids. Its SI unit is therefore W / (m² · K) (watts per square meter and Kelvin). The symbol used is usually (especially in mechanical engineering and process engineering ) or (especially in construction ). The heat transfer coefficient depends on the heat transfer coefficient between the solid body and the fluids as well as the thermal conductivity ( heat transfer coefficient ) and geometry of the solid body. The following statements apply to construction and are special cases of process engineering and thermal apparatus construction.
The heat transfer coefficient is a specific parameter of a component . It is mainly determined by the thermal conductivity and thickness of the materials used, but also by the thermal radiation and convection on the surfaces.
The measurement of the heat transfer coefficient takes place with a steady temperature profile (i.e. constant temperature on both sides) so that the heat storage capacity of the body does not falsify the measurement result.
The reciprocal of the heat transfer coefficient is the heat transfer resistance in m² · K / W.
- Depending higher the heat transfer coefficient, the worse is the thermal insulation of the body.
- The lower the heat transfer coefficient (= the higher the heat transfer resistance), the better the heat insulation property.
The heat transfer coefficient is particularly widespread in the building industry, where it is used to determine the transmission heat losses through components .
Definition and meaning
The heat flux density ( SI unit watt / meter ²) through a component that is exposed to the outside air temperature on one side and the inside air temperature on the other is proportional to the temperature difference in the steady state , with the proportionality constant :
The derived SI unit of the U-value is W / (m² · K) with the unit symbol W for the unit of measurement watt and K for Kelvin .
It thus describes the amount of thermal energy in joules (= watt seconds ). which is allowed to pass through a partition between two rooms over an area of one square meter over a period of one second if the temperatures on both sides are stationary (i.e. not only during the measurement second) by 1 K (corresponds to a difference of 1 ° C) distinguish. The unit watt seconds of energy is no longer explicitly used in the final unit of the U-value, as the time component ("seconds") in the energy unit is shortened against the time component in the denominator ("per second") . The unit could therefore also be understood as J / (s · m² · K).
The U-value defined in this way is therefore a measure of the “thermal permeability” or the thermal insulation properties of components, for example a specific glazing of a window. A component with a small U-value lets through less heat than a component with a larger U-value. The amount of heat that passed through the surface during the period is
The heat flux density between the media on both sides of a component is considered here (e.g. indoor air to outdoor air). If you do not want to determine the properties of the entire component, but rather those of the materials used (e.g. surface temperature inside to outside), then instead of the heat transfer coefficient of the component, its heat transfer coefficient should be used (see also below ).
Limitations of definition
The definition equation (1) assumes stationary conditions and is not suitable for calculating the current heat flux density at temperatures that change over time. During a heating process, for example, due to the heat storage capacity of the component, delay effects occur which are not taken into account when attempting to calculate the surface heat flows using equation (1). In the subsequent cooling process, however, the error occurs in the opposite sense. If the heating and cooling are symmetrical, the two errors cancel each other out. As can be seen, in the case of strictly periodic temperature changes, equation (2) still applies if it is used to calculate the amount of heat lost during a period and the mean temperature values and averaged over the period are used:
- (for periodic temperature changes)
The temperature changes that occur in reality are never strictly periodic, but the resulting error is only related to the slightly different heat content of the component at the beginning and at the end of the period under consideration and therefore remains limited. Compared to the total heat loss, which increases with increasing length of time, it is completely negligible if the building is exposed to climatic conditions under which it suffers a transmission heat loss on average over the long term:
- (for any temperature changes and sufficiently large )
Despite its definition, which is initially limited to stationary conditions, the U-value is therefore a suitable measure for the transmission heat losses accumulated over a longer period of time through the standard cross-section of a component, which are caused by different mean temperatures of the inside and outside air, even under real, unsteady conditions . This is the basis of its importance as an important criterion in the energetic evaluation of a building.
Comparison of stationary and unsteady behavior
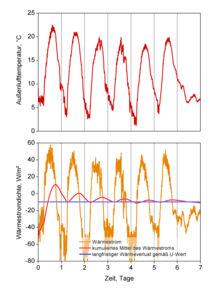
In the figure on the right, these relationships are illustrated using a specific example. A 40 cm thick solid brick masonry with a U-value of 1.2 W / (m² · K) is considered, which is exposed to the outside air temperatures shown in the upper part of the picture on the outside, while a constant temperature of 20 ° C is applied on the inside. The outside air temperatures are real five-minute measurement data from seven days in May 2006.
The orange curve in the lower part of the picture shows the heat flow through the outer surface of the wall, as determined by means of an unsteady calculation program in five-minute steps from the available data (positive currents flow into the wall, negative currents out). The strong fluctuations in the heat flow show the clearly unsteady character of the situation. The mean value of the outside air temperature during the seven days under consideration is 11.9 ° C. The U-value therefore indicates an average heat loss
ahead. This value is shown as a blue line. The red curve in the lower part of the picture shows the cumulative mean value of the heat flow, i.e. the mean value over five minutes, over ten minutes, over fifteen minutes, etc., until the mean value over the entire seven days is finally reached on the right-hand side. As can be clearly seen, as the averaging period increases, the transient fluctuations in the heat flow are quickly averaged away and within the seven days already approach the mean value predicted by the U-value almost perfectly.
The cumulative mean is initially systematically above the U-value result, because after previous cooler days (not shown here), warming up the wall initially required an above-average flow of heat into the wall. Even this deviation no longer plays a role after several days of averaging.
For the sake of simplicity, heat input from solar radiation was not included here. They could be taken into account, for example, by appropriately increasing the outside air temperatures (to so-called radiant air temperatures or combined outside temperatures ). This does not change the mathematical relationships or general behavior.
Calculation of the U-value of components and materials
The calculation of the heat transfer coefficient for the public law proof in the building industry is carried out according to the calculation steps according to EN ISO 6946 , which also deals with more complicated building-relevant cases. The required rated values are specified in EN 12524 and DIN 4108-4 .
Designations
Designations for heat transfer coefficients of windows , unit W / (m² · K):
- Kv value: old designation; typically 0.1 W / (m² · K) higher than U g
- U f value ( f for frame ): characteristic value for window frames; typical value: 1.3 W / (m² K)
- U g value ( g for glazing ): characteristic value for window glass (calculation method according to EN 673)
- U w value ( w for window ): characteristic value of the entire window
- ψ g value: thermal bridge between panes of glass ( warm edge )
- ψ e value: thermal bridge between window frame and masonry
U f value
The U f value is a modification of the general U value. The f stands for "frames" ( English frame ). What is meant is a window frame, usually consisting of the fixed frame part and the movable frame part.
The U f value can be determined by calculation, hot box measurement or a very simplified approximate method. The calculation of the U f value is based on the specifications of EN ISO 10077-2.
calculation
For the calculation (as well as for the measurement), the actual glazing (with thickness) is first exchanged for a calibration panel ( ) with the actual glass thickness ( ) in order to create comparable conditions. Other geometric specifications for the calculation are varied and regulated in EN ISO 10077-2. The two-dimensional thermal conductance is now determined in the stationary process based on a defined area and a temperature difference .
There are:
- Q : total heat flow in W / m
- L 2D : two-dimensional thermal conductance in W / (m K)
- : Temperature difference inside-outside in K
- U f : frame U-value in W / (m² · K)
- U p : Panel U-value in W / (m² · K) ( )
- : projected frame width in m
- : Panel length, from the end of the profile in m ( )
The greatest difficulty here is determining the total heat flow , which, due to the complex geometry of a window profile and cavities, which are difficult to calculate individually, can only be measured or calculated using the finite element method (FEM) .
Ideal wall
In the case of a flat, infinitely extended wall, which is composed of layers of thickness and thermal conductivity lying one behind the other , the proportionality constant is calculated according to:
With
- U : heat transfer coefficient in W / (m² · K)
- R T : thermal resistance in m² · K / W
- R se : external heat transfer resistance in m² · K / W
- d i : layer thickness of layer number i in m
- λ i : specific thermal conductivity of this layer in W / (m K)
- 1 ⁄ λ i = R λ, i : the specific thermal resistance of the i-th layer in mK / W
- d i ⁄ λ i =Ri: thethermal resistance ofthis layer in m² · K / W
- R si : internal heat transfer resistance in m² · K / W
Components
The heat transfer of a component depends on the thermal conductivity of the materials used and their layer thicknesses as well as on the component geometry (flat wall, cylindrically curved pipe wall, etc.) and the transition conditions on the component surfaces.
In general, the heat transfer resistance is the sum of the heat transfer resistances of the individual component layers lying one behind the other as well as the heat transfer resistances to the surrounding fluids (air, water, etc.) on the two surfaces and is the reciprocal of the heat transfer coefficient:
Measurement of the U-value of components and materials
The determination of precise heat transfer coefficients for the certification of building material parameters is carried out by material research and testing institutes on behalf of the manufacturer at complex test facilities in order to guarantee comparable conditions.
In addition, there are three other methods of assessing the quality of the building insulation on site (in situ): thermal imaging camera, multiple temperature measurements and heat flow measurement (U-value measurement).
Thermal camera
The thermal imaging process (also known as thermography ) is used to test the thermal insulation of houses, for building diagnostics and / or generating energy certificates for structural analysis of the masonry, for moisture detection in walls and roofs and for localizing cracks in pipelines. A thermal image helps to understand the general quality of the insulation of a building (identification of thermal bridges, inhomogeneous insulation layers). Thermal imaging cameras only measure thermal radiation, but not temperatures or thermal convection or thermal conduction; therefore they do not produce any data (e.g. U-value) that can be used for evaluating insulation. This technique can therefore only be used to roughly determine the U-value.
Multiple temperature measurements
With multiple temperature measurements inside and outside of the building and simplifying assumptions, a heat flow through a building element can be calculated. This heat flow allows the U-value to be determined. This method provides quantitative measurement results, but is only suitable for practical use for in-situ measurements in a few scenarios.
With a special temperature sensor for U-value determination, a compatible measuring device and another temperature sensor, the heat transfer coefficient (U-value) of a component can be determined non-destructively at the place of use (e.g. construction site). The following are determined for measuring the U-value:
- Outside temperature Ta
- Internal temperature Ti
- Surface temperature Tw of the component (inside).
A radio sensor is used to measure the outside temperature. All data are recorded and saved in the measuring device via a measuring program and then evaluated and documented with the aid of the software. The measurement of the respective temperatures and the determination of the differences is easy. The following requirements must be met for reasonably reliable measurement results:
- Temperature difference between inside and outside, ideal> 15 K
- constant conditions
- no sun exposure
- no heating radiation in the measuring range.
The night or early morning hours before sunrise are particularly suitable for multiple temperature measurements to determine the U-value.
Multiple temperature measurements - special case of windows
Another development for determining the U g value is the two-part U g value measuring device "Uglass" from Netzsch Gerätebau GmbH , which was developed together with the Bavarian Center for Applied Energy Research . The temperature difference between the inside and outside required for measurement is ensured here by actively heating one side of the glass. This means that the operating temperature range is between −10 ° C and +60 ° C. The measuring device can be used to determine the insulation values of all commercially available double and triple glazing with U g values between 0.5 and 4 W / (m² · K). The measurement accuracy of Uglass is in the range of ± 10% with U g values above 1.0 W / (m² · K). For U g values below 1.0 W / (m² · K), the measurement accuracy is ± 0.1 W / (m² · K). Measurement and evaluation are carried out automatically by the Uglass software.
Heat flow method
As soon as there is a temperature difference between two sides of a building element, heat flows through this material. The heat flow method is based on this effect and measures the U-value using a heat flow sensor (inner wall) and two temperature sensors (indoor air temperature and outdoor air temperature). Since temperature differences of 5 ° C are sufficient for reliable measurements, this method works in-situ and enables the simple calculation of the U-value of any building material. The heat flow method is described in standards (ISO 9869, ASTM C1046 and ASTM C1155). To perform measurements according to these standards, the measurement time must be at least 72 hours. For use among practitioners, a shorter duration may be sufficient (depending on the building material, thickness and temperature fluctuations on site). This is due to the fact that the U-value can reach a stable value before the required 72 hours for an ISO 9869-compliant measurement are reached. In combination with software, the measurement can be followed live on a laptop and the measured values can be used for other calculation programs. This means that the U-value, which is an indicator for assessing the thermal properties of the building envelope, can be measured without material destruction.
criticism
When determining the heat transfer coefficient, only temperature differences due to heat conduction are measured, but not heat losses or gains due to thermal radiation. Their influence (for example in the case of aluminum layers of thermal insulation materials reflecting infrared radiation ) on the thermal insulation is therefore only insufficiently taken into account. The comparability of the results and the relevance of the U-value for the assessment of the heat losses of a building is disputed by some despite clear measurements, even if they took part in the measurements themselves (Bossert).
Typical values of the construction industry
| Component | thickness | U-value in W / (m² · K) |
|---|---|---|
| External wall made of concrete without thermal insulation | 25 cm | 3.3 |
| Brick outer wall | 24 cm | about 1.5 |
| 36.5 cm | approx. 0.8 | |
| Outer wall made of masonry bricks (17.5 cm) with thermal insulation composite system (PUR) |
30 cm | approx. 0.32 |
| Outer wall made of highly porous perforated brick , unplastered | 50 cm | 0.17-0.23 |
| Outer wall timber frame construction , typical apartment structure | 25 cm | 0.15-0.20 |
| Outer wall made of solid wood (without thermal insulation) | 20.5 cm | 0.5 |
| Exterior wall made of aerated concrete | 36.5 cm | 0.183-0.230 |
| 40 cm | 0.163-0.210 | |
| 50 cm | 0.125-0.146 | |
| Inner wall made of masonry bricks | 11.5 cm | 3.0 |
| Inner wall made of aerated concrete | 28 cm | approx. 0.6 |
| External door made of wood or plastic | - | 3.49 |
| Acrylic glass (plexiglass) | 5 mm | 5.3 |
| Simply window | 4 mm | 5.9 |
| Double window | - | 3.0 |
| Windows with double glazing | 2.4 cm | 2.8-3.0 |
| Windows with thermal insulation glazing | 2.4 cm | approx. 1.3 |
| Total window Requirement energy certificate Switzerland (2011) | - | 1.3 |
| Light building element made of polycarbonate | 5 cm | approx. 0.83 |
| Passive house standard windows | - | 0.5-0.8 |
Importance for thermal protection
According to the ordinance amending the Energy Saving Ordinance (EnEV), which came into force in Germany on October 10, 2009 , the annual primary energy demand Q P and the specific transmission heat loss H ' T (for non-residential buildings: mean heat transfer coefficients of the heat-transferring surrounding areas according to the type of component) complying with certain limit values. U-values are included in the calculation of the transmission heat loss and this in turn is used in the calculation of the primary energy demand. Furthermore, the EnEV stipulates limit values for the heat transfer coefficient of certain components if these are replaced or newly installed in existing buildings.
Norms
- EN ISO 6946 Building components - Thermal resistance and thermal transmittance - Calculation method
- EN ISO 7345 , as DIN: 1996-01 Thermal insulation - physical quantities and definitions (replaces DIN 4108-1)
- EN ISO 9346 Thermal insulation - Mass transfer - Physical quantities and definitions
- EN ISO 10077-2 , as DIN: 2012-06: Thermal behavior of windows, doors and shutters - Calculation of the thermal transmittance - Part 2: Numerical method for frames
- EN 673 , as DIN: 2011-04 Glass in building - Determination of the heat transfer coefficient (U-value) - Calculation method
- EN 12524 Building materials and products - Thermal insulation properties - Tabulated rated values
- DIN 4108 thermal insulation in building construction , places further requirements on the U-values of components, but not with the aim of saving energy, but rather the avoidance of structural damage ( minimum thermal insulation )
literature
- W. Heindl: The thermal protection of a flat wall in case of periodic thermal loads (1st part). In: The brick industry. Issue 18, 1966, pp. 685-693.
- W. Heindl: On the unsteady thermal behavior of thermal bridges - or: Does the heat storage capacity of components with multi-dimensional heat conduction have an influence on the transmission heat losses? In: Building Physics. Volume 4, 1982, pp. 145f.
- M. Reick, S. Palecki: Extract from the tables and formulas of DIN EN ISO 6946 . Institute for Building Physics and Materials Science. University of Essen. Status: 10-1999. ( online ; PDF; 168 KB)
- T. Richter, S. Winkelmann-Fouad: Use of the U-value as a parameter for heat transport processes. In: E. Cziesielski (Ed.): Building Physics Calendar 2005 . Ernst & Sohn, Berlin 2005, ISBN 3-433-01722-0 .
Web links
- Easy online U-value calculation at energiesparhaus.at
- Definition and formulas for calculating the k-value on baustoffkunde.info
- Introduction to U-value calculation and online calculator at www.Bastelitis.de
- Free demo version of the online U-value calculation on U-Wert.net
Individual evidence
- ↑ EN ISO 6946 according to Reick, Palecki; see standards and literature
- ↑ W. Heindl: The thermal protection of a flat wall with periodic heat loads (1st part) . In: The brick industry. Issue 18, 1966, pp. 685-693.
- ↑ W. Heindl: On the unsteady thermal behavior of thermal bridges - Or: Does the heat storage capacity of components with multi-dimensional heat conduction have an influence on the transmission heat losses? In: Building Physics. Volume 4, 1982, pp. 145f.
- ↑ J. Ebel: The U-value: only stationary or also unsteady. In: bauzeitung. 56, H. 3, 2002, pp. 56-60.
- ↑ J. Ebel: EnEV, solar radiation and Boltzmann emission. In: Building Physics. 25, H. 5, 2003, pp. 306-310.
- ↑ Window: Determine the total U-value
- ↑ greenTEG AG: U-Value Measurements with greenTEG's U-Value Kit. Retrieved July 4, 2017 .
- ↑ Guido F. Moschig: Building renovation. Vieweg + Teubner Verlag, 2008, ISBN 978-3-8351-0183-8 , pp. 101f. (books.google.at)
- ↑ EMPA : Influence of the heat storage capacity of the outer wall on the solar energy gain. EMPA investigation report No. 136,788. December 1994.