Wave packet

Propagation of a one-dimensional wave packet without dispersion

A wave packet , a wave group or a wave train is a spatially or temporally limited wave . Mathematically, a wave packet can be understood as a composite system of simpler waves. In particular, a wave packet can be represented by superposition (addition) of several plane waves . This decomposition of the wave packet according to frequency components is motivated by the Fourier transformation and can be determined experimentally with a spectrometer . The speed at which the envelope of a wave packet moves is called the group speed .

Mathematical formulation

Dispersion behavior of a wave packet, above without dispersion, below with dispersion

plane or monochromatic wave (real part / cos wave)

A wave packet that is composed of a superposition of different monochromatic waves (see figure above).

A wave packet can be represented as the sum of plane waves: ${\displaystyle \psi (x,t)}$

${\displaystyle \psi (x,t)=\sum \limits _{j}C_{j}\cdot e^{\mathrm {i} (\omega _{j}\cdot t-k_{j}\cdot x)}}$

Are there

• the amplitudes of each individual plane wave are arbitrary and determine the special structure of the wave packet, especially the more or less narrow limitation of the spatial extent. ${\displaystyle C_{j}}$
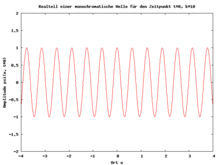
• the individual plane waves each monochromatically with the angular frequency ; the wave packet as a whole, however, does not have a single frequency, but a frequency distribution . ${\displaystyle \omega _{j}}$
• the wave number given by . It is the phase velocity of the plane wave, depending on the medium may be a function of frequency ( dispersion , leads to the bleed of the wave packet with time). If it is frequency-independent, the medium is free of dispersion and the wave packet does not change its shape over time (see first illustration). ${\displaystyle k_{j}}$ ${\displaystyle k_{j}=\omega _{j}/c(\omega _{j})}$ ${\displaystyle c(\omega )}$ ${\displaystyle c}$ ${\displaystyle \psi (x,t)}$

The phase velocity can also be expressed with the refractive index by the formula . This results in the shape of the wave packet ${\displaystyle n}$ ${\displaystyle n={\tfrac {c_{0}}{c(w)}}}$

${\displaystyle \psi (x,t)=\sum \limits _{j}C_{j}e^{\mathrm {i} (\omega _{j}\cdot t-{\frac {w_{j}\cdot n(w_{j})}{c_{0}}}\cdot x)}.}$

This means that the following statement can be made: "If a medium has a constant refractive index , the wave packet will not dissipate (no dispersion)". ${\displaystyle n(\omega _{j})={\text{const}}}$

Only the absolute square, the real part or the imaginary part of are physically meaningful . ${\displaystyle \psi }$

A wave packet is, just like a plane wave, a solution to the general wave equation

${\displaystyle {\frac {\partial ^{2}\psi }{\partial x^{2}}}={\frac {1}{c^{2}}}\cdot {\frac {\partial ^{2}\psi }{\partial t^{2}}}}$

This results from the linearity of the wave equation, it results in the superposition principle .

With a continuous frequency distribution one goes from the sum to the integral . It defines the amplitude distribution, which now depends on the wave number : ${\displaystyle C(k)}$ ${\displaystyle k}$

${\displaystyle {\text{(1)}}:\,\psi (x,t)=\int _{-\infty }^{\infty }C(k)\cdot e^{\mathrm {i} (\omega t-k\cdot x)}\mathrm {d} k}$

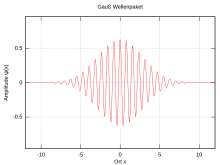
Example: Gaussian wave packet

Gaussian wave packet

A frequently used example of a wave packet is the Gaussian wave packet. This is a wave whose amplitude distribution is a Gaussian distribution . ${\displaystyle C(k)}$

A special feature of the Gaussian wave packet is that the Fourier transformation of a Gaussian function results in a Gaussian function again. The specification of a Gaussian amplitude distribution thus leads to a Gaussian wave in the spatial area . Conversely, if a wave packet in spatial space is given the Gaussian form, the frequency distribution of this wave packet is automatically Gaussian.

In addition, the Gaussian wave packet is the wave packet with the least blurring . I.e. with no other wave packet is the product of the width of the wave in spatial space and its width in frequency space smaller.

Mathematically

If one sets a Gaussian function for the amplitude distribution in equation (1) above

${\displaystyle C(k)=e^{-{\frac {(k-k_{0})^{2}}{(2/a)^{2}}}}}$

one, after the integration at the time : ${\displaystyle t=0}$

${\displaystyle \psi (x,0)=\left({\frac {2}{\pi a^{2}}}\right)^{1/4}\cdot e^{-x^{2}/a^{2}}\cdot e^{i\cdot k_{0}\cdot x}}$

The figure on the right shows the result. You now only have one area in which the amplitude is noticeably different from 0.

Dispersion

Reflected impulses with unloaded cable

Most of the time, the speed of propagation of the wave depends on the wavelength or frequency (e.g. light in matter), so that the wave packet "dissolves", ie. H. its width becomes larger (or smaller) over time and the spatial definition becomes more and more imprecise. Wave packets that show no dispersion, i.e. that retain their shape and width, are also referred to as solitons .

The following experiment can be used to prove that electromagnetic waves propagate over an extremely large wavelength range from a few centimeters to a few kilometers (frequency range 20 kHz to around 2 GHz) at the same speed, so that there is no dispersion for electromagnetic waves in a coaxial cable : A Pulse generator generates short voltage pulses of around 10 ns duration at a repetition frequency of around 20 kHz. If these are sent through a 20 m long coaxial cable, they are reflected at the open end and run back again. Depending on the cable attenuation, around a hundred pulses can be observed whose shape does not change. The unavoidable ohmic losses in the cable and at the connection resistance between generator and cable cause a certain decrease in amplitude but no change in shape of the envelope of the wave packets.

A Fourier analysis can be used to determine the frequency content of the very short voltage pulses:

• The lowest frequency is the repetition frequency of the impulses, i.e. 20 kHz.
• The highest frequency is around 100 times the reciprocal of the pulse width, i.e. 10 GHz in the case assumed above.

If the travel time of the pulses were to differ noticeably due to dispersion, the waveform of the pulses would also have to change according to the laws of Fourier synthesis . Since this is not observed, it follows that the propagation speed in the cable remains constant in the frequency range described.

Applications

• Water waves :
  Wave packets are used as surface waves in water, for example to measure the transfer functions (RAO = Response Amplitude Operator ) of ships and offshore structures in model tests. The fact that all waves emanating from the wave machine meet at the same time in the same place is only possible because, according to the dispersion relation , short (high-frequency) waves propagate more slowly on the water surface than long (low-frequency) waves. (Few) shipbuilding research institutes act as service providers for such model tests .
• Matter waves :
  In quantum mechanics , wave packets are used to represent particles in a wave image. The widths of a wave packet in the spatial and momentum space are linked to one another via the Heisenberg uncertainty principle . A spatially well-determined particle therefore has a very broad momentum distribution and vice versa. The same goes for energy (frequency) and time.

Multi-dimensional wave packet

Equation (1) can also be expressed in vector terms:

${\displaystyle {\vec {\psi }}({\vec {x}},t)=\int _{-\infty }^{\infty }\mathrm {d} k_{x}\int _{-\infty }^{\infty }\mathrm {d} k_{y}\int _{-\infty }^{\infty }\mathrm {d} k_{z}{\vec {C}}({\vec {k}})\mathrm {e} ^{\mathrm {i} (\omega t-{\vec {x}}\cdot {\vec {k}})}}$

At the point in time , an initial pattern can be   impressed on the space (generator), which is then propagated spatially for all subsequent time steps (iterator) using Huygens' principle . ${\displaystyle t=0}$ ${\displaystyle C({\vec {x}})=\operatorname {FT} [C]({\vec {k}})}$

Wave train

A wave train is understood to be a time-limited (permanent ) wave of a frequency . Although all oscillations of the wave train have the same period , the spectrum of the wave train does not consist solely of the frequency component . From the Fourier theory follows a minimum width of the frequency spectrum with the time limitation : ${\displaystyle \Delta t}$ ${\displaystyle f}$ ${\displaystyle 1/f}$ ${\displaystyle f}$ ${\displaystyle \Delta f}$

${\displaystyle \Delta t\cdot \Delta f\geq 1}$( Küpfmüller's uncertainty relation ).

literature

• Wolfgang Demtröder : Experimental physics 3. Atoms, molecules and solids . 3. Edition. Springer, New York / Berlin / Heidelberg 2005, ISBN 3-540-21473-9 .

Remarks

1. ↑ The amplitude (capital letter) of the j-th frequency component must not be confused with its phase velocity (lower case letter). The symbols used here are common in this form. In the theory of the Fourier transform, the complex coefficients are referred to as. The real and imaginary parts, however, often with and . ${\displaystyle C_{j}}$ ${\displaystyle c(\omega _{j})}$ ${\displaystyle C_{j}}$ ${\displaystyle A_{j}}$ ${\displaystyle B_{j}}$
2. ↑ FT [.] Stands for the Fourier transformation

Individual evidence

1. ^ Stöcker: Taschenbuch der Physik . 6th edition. Verlag Harry Deutsch, 2010, ISBN 978-3-87171-860-1 . , Section 10.3.4 "Waves with different frequencies"
2. ↑ 2D wave packet simulation with finite resolution of space and time.
3. ↑ Clemens Schaefer: Electromagnetism . 8th edition. Walter de Gruyter, 1999, p. 399 ( limited preview in Google Book search).