Two-digit link
A two-digit link , also called a binary link , is a link in mathematics that has exactly two operands . Two-digit links occur very frequently , especially in algebra, and there is also an abbreviation of linkage without the addition of two-digit . But there are also links with a different arity , which link three or more operands with one another, for example.
definition
A two-digit link is a mapping of the Cartesian product of two sets and a third set . Such a link assigns an element to each ordered pair of elements and as the two operands with as the result of the link. If the sets , and are equal, the connection is also called an internal connection; otherwise one speaks of an external connection.
Spellings
Two-digit links are often written in infix notation instead of the usual prefix notation . For example one writes an addition as instead of . A multiplication is often written without any symbol so . The best-known postfix notation is the reverse Polish notation , which does not require brackets. The chosen spelling, whether prefix, infix, or postfix, essentially depends on the usefulness in the given context and the respective traditions.
Examples
- The basic arithmetic operations (addition, multiplication, subtraction and division) on corresponding sets of numbers are two-digit combinations. For example, dividing an integer by a natural number creates a rational number . This corresponds to a link .
- The composition of figures is a two-digit link: it assigns each figure and each figure its execution one after the other . This corresponds to a link . The quantities , and can be chosen as desired. This connection occurs in almost all areas of mathematics and forms the basis of category theory.
Inner two-digit link
An inner two-place link or two-place operation on a set is a two-place link that assigns an element of to every ordered pair of . This corresponds to the above general definition in the special case . The additional attribute inner expresses that all operands are from the set and the link does not lead out. It is said to also be completed with respect .
Inner two-digit links are an important part of algebraic structures that are studied in abstract algebra . They occur with semigroups , monoids , groups , rings and other mathematical structures .
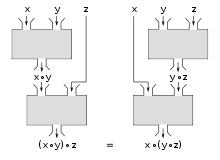
In general, a set with any internal connection is also called magma . Such links often have other properties, for example they are associative or commutative . Many also have a neutral element and invertible elements .
Examples
- The addition and the multiplication of whole numbers are internal connections or . The same is true for the natural , rational , real, and complex numbers .
- The subtraction of whole numbers is an inner link . The same is true for the rational , real, and complex numbers . Note, however, that the subtraction of natural numbers leads out of the set of natural numbers and is therefore not an internal connection. (Here is for example ).
- The division of rational numbers without is an internal connection . The same applies to the real and complex numbers without . Note, however, that the division of whole numbers leads out of the set of whole numbers and is therefore not an internal connection. (Here is for example ).
- For a given set the averaging and the union of subsets are internal connections on the power set .
- For any crowd , the composition of images is an inner link .
Outer two-digit links of the first kind
An outer two-place link of the first kind is a two-place link which is called the right operation of on , or which is called the left operation of on . They differ from inner two-digit links in that the set called the operator area , the elements of which are called operators , is not necessarily a subset of , i.e. it can come from outside . We then say operated from the right or from the left on and the elements of hot right or left operators .
Each operator defines exactly one mapping or which is also called the transformation to . In the case of a multiplication , instead of or , one writes briefly or and there is usually or no longer a distinction between the operator and the associated transformation . One then writes in the so-called operator notation : resp.
Examples
- For every natural number an inner - digit connection is always also an outer two-digit connection of the first kind, namely both a right and a left operation of on (it is always ). Such internal links are therefore also generally referred to as -digit operations . A zero-digit link can be viewed as an inner link and therefore always count as a zero-digit operation .
- A group operation is a group and a set. One also demands a certain compatibility of this operation with the group structure namely and for all and the neutral element of
- In linear algebra , the operator domain for scalar multiplication is a field , usually or and an Abelian group, for example or. In addition, a corresponding compatibility of the scalar multiplication with the already given structures and equipped with the operation becomes a vector space
comment
The term operation or operator is used e.g. B. in functional analysis , also for general two-digit links or used. Here are sets with the same (mostly algebraic ) structure , and often the transformation or with the structure should be on and compatible .
Outer two-digit links of the second kind
An outer two-digit link of the second kind is a mapping, that is , a two-digit link on a set but does not have to be closed with respect to it, so it may also apply.
Examples
- Every inner two-place link is also an outer two-place link of the second kind.
- The scalar product in the - dimensional - vector space assigns a real number to two vectors from and is thus an outer two-digit combination of the second kind. For the scalar product is also an inner two-digit combination, but not for.
- The scalar product in division ring of quaternions is an internal binary operation and thus an external binary operation of the second kind. Summing up against it as a four-dimensional division algebra over on, then the dot product is no internal link more, but it remains an external binary operation of the second kind.
- If an affine space is over a vector space , then with is an outer two-place link of the second kind.
See also
literature
- Gert Böhme: Algebra (= application-oriented mathematics . Volume 1 ). 4th, verb. Edition. Springer, Berlin / Heidelberg / New York 1981, ISBN 3-540-10492-5 , pp. 80 .
- F. Reinhardt, H. Soeder: dtv-Atlas Mathematik . 11th edition. tape 1 : Fundamentals, Algebra and Geometry . Deutscher Taschenbuchverlag, Munich 1998, ISBN 3-423-03007-0 , p. 38-41 .
- Günter Scheja, Uwe Storch: Textbook of algebra: including linear algebra . Part 1. Teubner, Stuttgart 1980, ISBN 3-519-02203-6 , pp. 101, 204-207 .
- Bartel Leendert van der Waerden : Algebra I . 9th edition. Springer, Berlin / Heidelberg / New York 1993, ISBN 978-3-662-01514-8 , pp. 146-148 .