Ribbon model
The band model or energy band model is a quantum mechanical model for describing electronic energy states in an ideal single crystal . The atomic cores are in a strictly periodic lattice. There are several energy ranges in which many quantum-physically possible states exist, which are energetically so close that they can be viewed as a continuum - as an energy band . The associated representation is called a band diagram . The energy band model of a solid is then the band structure shown in the momentum space (see below at Ek diagram ).
Origin of the tapes
Looking at a single atom , the energy levels of the atom are in discrete form. This also applies to atoms that are far apart. If two atoms are brought closer to each other, the observed effect is similar to that of coupled pendulums , in which the number of possible oscillation frequencies increases. With atoms in the lattice and when approaching from a certain distance, the atomic electron levels split due to the electrostatic interaction of the electrons (which corresponds to the coupling spring of the coupled pendulums) of the two atoms. The energy levels shift slightly up and down (see two-state system ). If you now look at a crystal in which a large number of atoms interact with one another, the number of permitted energy states increases accordingly, they merge into common energy bands.
This is the simplified, clearer explanation. Physically exact, the ribbons are not created by electrostatic interaction, but by superposition of the atomic orbitals if they overlap sufficiently, or in other words: from the solution of the Schrödinger equation for a single electron in the field of the ion cores .
The width of the energy bands is not the same for the different atomic energy levels. The reason for this is the different strengths of the bond between the electrons and their atom. Electrons at low energy levels are more strongly bound and interact less with neighboring atoms. This leads to narrow bands. The valence electrons in the valence band are bound more easily and can therefore easily overcome the potential mountains between the atoms. They interact strongly with those of the neighboring atoms and can no longer be assigned to a single atom in a crystal, these bands become wider, see figure.
See also: model of the quasi-free electrons
Basics for the conduction process of electrical charges
When considering the electrical properties of a crystal, it is important whether the energy levels in the outer, energetically highest energy bands (the valence and conduction bands) of the crystal are unoccupied, partially or fully occupied. A fully occupied belt, just like an unoccupied belt, does not contribute to the transport of cargo. The reason for this is that electrons in fully occupied bands have no energy, e.g. B. through an electric field, because there are no unoccupied states with slightly higher energy. Only a partially occupied band enables a net current other than zero in the electric field. However, this is only a necessary condition for the flow of current, as so-called Mott insulators with partially occupied bands show. To explain this, electronic correlation effects must be taken into account that are outside the validity of the band model as "one-electron dispersion" of the solid.
The good electrical conductivity of metals (even at low temperatures) is due to the only partially occupied conduction band (monovalent metals). In the case of multi-valued metals, it can happen that the corresponding band would theoretically be fully occupied, but with metals this band overlaps with the next higher band. In both cases, the bands are only partially occupied, so that free energy levels are available for charge transport. In both cases, the Fermi level is in the outer band that is still occupied.
Even with semiconductors and insulators at absolute zero (temperature), the highest energy band is completely occupied by electrons; this band is called the valence band . In contrast to metals, this band does not overlap with the next higher band, the unoccupied conduction band at absolute zero. There is a quantum mechanically “forbidden area” between the two bands , which is called the band gap . Since the valence band is fully occupied at 0 K, no charge transport can take place. If the material is supplied with sufficient energy by increasing the temperature or by exposure to light, electrons can overcome the band gap and be raised into the conduction band. In this way, an unoccupied trunk band can be partially occupied. These electrons and the holes remaining in the valence band both contribute to the electric current ( intrinsic conduction ).
Classification based on the position of the bands
Insulators and semiconductors
A crystalline dielectric (also known as an insulator ) has an unoccupied conduction band and such a large band gap ( E G > 3 eV) that only very few electrons are thermally excited from the valence to the conduction band at room temperature and even at significantly higher temperatures. The specific resistance of such a crystal is very high. However, by supplying a sufficient amount of energy , i.e. at (very) high temperatures or by applying a sufficiently high voltage, any insulator can become a conductor, but this is then destroyed.
The situation is similar for a crystalline semiconductor , but the band gap here is so small (0.1 eV < E G <3 eV) that it can be easily overcome by supplying thermal energy or absorbing a photon ( photo semiconductor ). An electron can be lifted into the conduction band and is mobile here. At the same time, it leaves a gap in the valence band that can be filled by neighboring electrons. Thus the gap is movable in the valence band. They are also known as defect electrons , electron defects or holes (see hole conduction ). As a result, a semiconductor exhibits low intrinsic conductivity at room temperature , which can be increased by increasing the temperature.
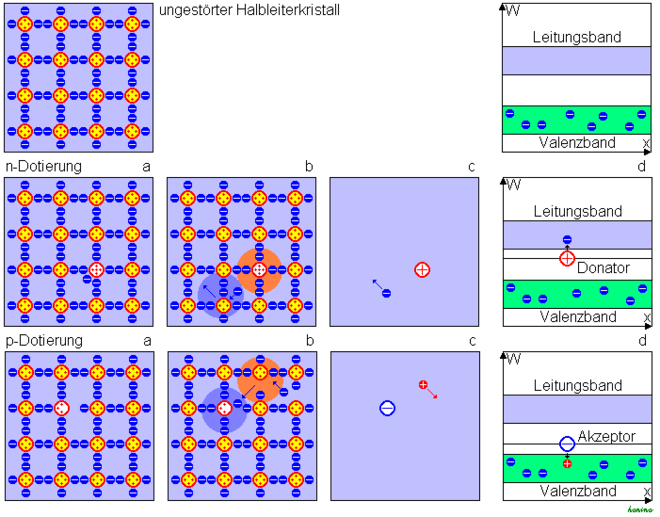
A semiconductor can be specifically equipped with charge carriers by doping . The semiconductor crystal is based on a crystal lattice made up of 4- valent atoms, each bound by four electron pairs. Doping with pentavalent atoms leaves an electron in the lattice that is not required for binding and is therefore only loosely bound (figure below, figure a). It can therefore be lifted into the conduction band with only little energy and is mobile here (Fig. B). Such an atom is called an electron donor ( Latin donare , to give). The crystal is equipped with mobile negative charge carriers, one speaks of n-doping. At the same time, a positive atomic core remains in the lattice. If the background of the neutral basic substance is disregarded (Fig. C), a positive fixed and a negative mobile charge have been introduced into the grid. In terms of energy, a donor lies just below the conduction band, as little energy is required to excite the conduction band due to the weak bond of the “additional” electron (Fig. D).
Doping with 3-valent atoms leads to an unsaturated bond in which one electron is missing. This can be torn from another bond with little energy expenditure. Such an atom is called an electron acceptor (Latin: accipere , to accept), which is energetically just above the valence band. A negative stationary charge is created. At the same time, the electron leaves a gap in the crystal that can be filled by another electron, i.e. a movable electron defect. The result is a negative fixed and a positive mobile charge. One then speaks of p-doping.
The doped crystals find an important application in microelectronics , the structures of which are mainly based on semiconductor diodes . These are formed from a pn junction , i.e. from a combination of a p-doped and an n-doped crystal.
However, there are also semiconductors (and insulators) to which the ribbon model does not apply. These include, for example, so-called hopping semiconductors, with which the dominant mechanism for charge carrier transport is hopping (English for 'hopping'). The electrons therefore do not “wander” from one place to another through the conduction band, but rather “jump” from atom to atom, so to speak.
Metals and semi-metals
In a metal , one usually does not speak of a conduction or valence band. However, it also applies here that the highest fully occupied band is the valence band. The partially occupied band above can be referred to as the conduction band.
In monovalent metals, the highest occupied energy band is half filled. In the case of polyvalent metals, the outer energy bands partially overlap. Electrons can therefore change to a higher energy state when any small electrical field strengths are applied (move freely, so to speak) and contribute to the flow of electrical current, which is why metals are good electrical conductors. An increase in temperature generally leads to a decrease in the conductivity of the crystal, since the increased scattering of the electrons results in a lower average speed. In the case of metals or semi-metals, the Fermi level is within the highest occupied band or in the overlap area of the bands.
In the case of semi-metals , the lower edge of the conduction band is only slightly lower than the upper edge of the valence band. Even at temperatures around absolute zero, this small overlap leads to a low concentration of electrons in the conduction band and holes in the valence band.
Ek diagram
In the figures above, the energy levels are plotted one-dimensionally over the position coordinate . For the consideration of the processes when an electron leaps from one band to another, however, the representation using the wave vector has proven itself. This is explained in more detail under the heading of band structure .
history
The ribbon model of electron conduction in metals was developed in 1928 by Felix Bloch (in his dissertation with Werner Heisenberg in Leipzig), at that time still as a one-electron model in periodic potential, he only considered the ground state ribbon and no interaction of the electrons with one another. This was done independently and simultaneously in 1928 by Hans Bethe in his Munich dissertation with Arnold Sommerfeld. In the following years it was further developed by Rudolf Peierls (from 1929 with Heisenberg in Leipzig), Léon Brillouin and Alan Herries Wilson (1931). Wilson also looked at insulators and semiconductors in terms of band structure. Realistic band structure calculations began with a work by Eugene Wigner and Frederick Seitz on the sodium grid in 1933, in which the Wigner-Seitz cell was also introduced. Early researchers in the field included John C. Slater at MIT and Nevill Mott and Harry Jones in Bristol.
Web links
- What is the ribbon model? ( Memento from May 1, 2010 in the Internet Archive )
Individual evidence
- ^ A b Hans-Jürgen Bargel, Hermann Hilbrans (Hrsg.): Material science . 10th edited edition. Springer, Berlin et al. 2008, ISBN 978-3-540-79296-3 , p. 11 ( limited preview in Google Book search).
- ↑ a b Wolfgang Demtröder : Atoms, Molecules and Solids (= Experimentalphysik . Volume 3 ). 3rd, revised edition. Springer, Berlin et al. 2005, ISBN 3-540-21473-9 , pp. 441 ( limited preview in Google Book search).
- ^ Rudolf Gross, Achim Marx: Solid State Physics . Walter de Gruyter GmbH & Co KG, 2014, ISBN 978-3-11-035870-4 ( limited preview in the Google book search [accessed on December 23, 2016]).
- ↑ Heinrich Frohne, Karl-Heinz Locher, Hans Müller, Franz Moeller: Moeller Fundamentals of Electrical Engineering . Springer-Verlag, 2005, ISBN 978-3-519-66400-0 ( limited preview in the Google book search [accessed December 23, 2016]).
- ↑ Hansgeorg Hofmann, Jürgen Spindler: Materials in electrical engineering: Fundamentals - structure - properties - testing - application - technology . Carl Hanser Verlag GmbH & Company KG, 2013, ISBN 978-3-446-43748-7 ( limited preview in the Google book search [accessed December 23, 2016]).
- ^ AF Holleman , E. Wiberg , N. Wiberg : Textbook of Inorganic Chemistry . 101st edition. Walter de Gruyter, Berlin 1995, ISBN 3-11-012641-9 , p. 1313.
- ↑ Erwin Riedel , Christoph Janiak: Inorganic Chemistry . 7th edition. Walter de Gruyter, Berlin a. a. 2007, ISBN 978-3-11-018903-2 , pp. 724 ff .
- ↑ Felix Bloch: About the quantum mechanics of electrons in crystal lattices . In: Journal of Physics . tape 52 , no. 7–8 , July 1, 1929, pp. 555-600 , doi : 10.1007 / BF01339455 .
-
↑ On the story: Lillian Hoddeson u. a. (Ed.): Out of the Crystal Maze. Chapters in the history of solid state physics . Oxford University Press 1992, Chapter 2: Lillian Hoddeson, Gordon Baym, Michael Eckert: The development of the quantum mechanical electron theory of metals 1926-1933. 88-181, Chapter 3: Paul Hoch: The development of the band theory of solids 1933-1960. Pp. 182-235.
See also: Lillian Hoddeson, Gordon Baym, Michael Eckert: The development of the quantum-mechanical electron theory of metals: 1928-1933 . In: Reviews of Modern Physics . tape 59 , no. 1 , 1987, pp. 287-327 , doi : 10.1103 / RevModPhys.59.287 .