Fusion by means of magnetic inclusion

Fusion by means of magnetic confinement is the most widely pursued development path for the technical production of electrical energy from nuclear fusion . Concepts of generating commercially usable electrical power with a reactor based on magnetic confinement are also known as magnetic fusion energy , or MFE for short. In general, the way to generate fusion energy by magnetic confinement is considered to be more advanced and more promising than inertial fusion, which was also investigated .
In the projects currently being specifically pursued to fuse lighter atomic nuclei into heavier ones, the hydrogen isotopes deuterium and tritium are used, which are converted into helium -4 (see also nuclear fusion reactor ). A single fusion reaction occurs when a deuterium and a tritium nucleus come very close. Because of the mutual electrostatic repulsion of the positively charged nuclei, this can only be achieved with a very high kinetic energy of the reactants in the range of 10 to 20 keV , which corresponds to temperatures of around 100–250 million degrees Celsius. At these temperatures atomic nuclei and electrons are separated from each other and form a plasma .
Such a plasma cannot be enclosed in material vessels, since if it touched the cold walls it would immediately cool down so much that the plasma state is ended. One way to confine such a hot plasma is to use appropriately shaped magnetic fields. Their action ( Lorentz force ) on the moving, charged plasma particles can keep them away from the vessel wall. If one regards the plasma in its magnetic vessel as a fluid , then its outwardly directed pressure is compensated for by the inwardly directed magnetic field pressure (a formal arithmetic variable, not to be understood clearly as mechanical pressure). The necessary plasma pressure of the order of magnitude of 1 bar could be maintained for seconds to minutes in previous experiments.
From the variety of possible magnetic field arrangements, two concepts with toroidal geometry have emerged as the most promising: the tokamak and the stellarator . The greatest of these experiments are
- the tokamak JET (in operation since 1983), with which fusion power on a megawatt scale was briefly generated,
- the Heliotron LHD (in operation since 1998),
- the Wendelstein 7-X stellarator (in operation since 2015), which is supposed to maintain a stable plasma with fusion-relevant parameters for 30 minutes,
- the tokamak ITER (construction started in 2006, planned completion 2025 ), with which the first fusion power “net” (i.e. exceeding the heating power requirement) is to be generated.
All research efforts to date are aimed at generating stable plasmas in the temperature range mentioned for a longer period of time. Except in a few experiments in the TFTR ( Tokamak Fusion Test Reactor , USA) and JET plants, no deuterium-tritium mixture has been used, but ordinary hydrogen or, in some cases, pure deuterium.
Plasma confinement by magnetic fields
Fusion with magnetic confinement is based on the Lorentz force . This holds the charged plasma particles, electrons and ions , in the magnetic field on helical paths. Such a particle trajectory can be imagined as a combination of a movement along a magnetic field line and - perpendicular to it - a circular movement around the field line (gyration).
The simplest magnetic confinement can be achieved with a long solenoid . The magnetic field of such a coil is directed parallel to the coil axis; it prevents the loss of the particles in the radial direction, but not along the axis, i.e. at the coil ends. There are essentially two methods of avoiding these end losses. One tries to build up magnetic mirrors at the coil ends, with the other one bends the solenoid to a certain extent into a closed ring ( torus ).
Magnetic mirrors
An active area of research in the early years of fusion research were magnetic mirror arrangements (technical jargon: "mirror machines"), as these have great advantages over toroidal arrangements in practical and technical terms, e.g. B. in terms of maintenance work and replacement of parts. Most of the mirror machines designed tried to confine the plasma at the ends of the coil by non-planar magnetic fields. Although the simple mirror with its bottle neck-shaped course of the field lines is not sufficient to hold the hot fusion plasma in place, with additional magnets of more or less complicated shape it can be achieved that the field lines are largely bent back inside the confinement volume, so that fast particles can also be made stay locked up. For reasons of symmetry, however, there is a point that is permeable to the particles in every mirror configuration. This clearly means that there is a field line that is not closed inside the vessel, but leads out of the confinement area. Even advanced designs (e.g. in the MFTF experiment) can never completely prevent this.
Toroidal arrangements
An exclusively toroidal magnetic field cannot include charged particles because of the gradient and curvature drift (see figure): In a toroidal arrangement of coils, the magnetic field strength is necessarily higher on the inside, where the coils are closer together, than on the outside. The electrons and ions therefore do not perform exactly circular screw movements around the field lines, but the curvature of their screw paths is somewhat narrower towards the inside of the torus than outside. The particle trajectories of electrons and ions therefore drift up and down as shown in the figure. The resultant charge separation creates an electric vertical field. This electric field, together with the magnetic field, leads to another drift, which brings the particles outwards and thus destroys the confinement.
The way out is to use a poloidal component of the magnetic field in addition to the toroidal component, so that the magnetic field lines wind helically around the torus. The plasma particles following their field line thus experience alternating drifts towards the plasma center and away from it, so that overall no charge separation takes place.
A distinction is made between the tokamak and the stellarator as to how the poloidal magnetic field component is generated: In the tokamak, this is caused by an induced current flowing in the plasma (with disadvantages for plasma stability), in the case of the stellarator, particularly complex magnetic coils.
An early attempt to build a system for magnetic confinement was the stellarator developed by Lyman Spitzer in 1951 (from the Latin stella "star", as an allusion to the generation of energy by nuclear fusion in stars). This essentially consisted of a torus divided into two half-rings, the halves of which were connected to form a figure eight by two straight, crossing tubes. The result of this is that particles that migrated from the inside to the outside during the orbit through the half eight are again inside when they enter the other half of the eight. In newer stellarator concepts, the averaging of this drift is achieved in that the magnetic field causes the plasma to constantly rotate around its own axis following the center circle.
In 1968 the Russian research results on the tokamak were published for the first time , with results that far overshadowed all previously competing fusion reactor concepts, whether magnetic or not. Since then, the tokamak principle has been the most widely used concept for magnetic confinement. In a tokamak, a poloidal field is created by a current flowing in the plasma. This poloidal field, together with the toroidal field generated by coils, leads to the twisting of the field lines. In contrast to the stellarator, where the magnetic field has a three-dimensional structure, in the tokamak it is two-dimensional, i.e. H. it is rotationally symmetrical about the torus axis.
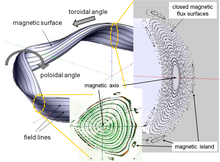
In the toroidal enclosure, the helically twisted magnetic field lines form onion-like nested magnetic flux surfaces around the central magnetic axis. Since the field lines cannot intersect, a fixed twist ( rotation transformation ) can be assigned to each river area . Without further disturbances, a charged particle would always move on the same flux surface on which it rotates toroidally and poloidally. This creates an equilibrium between the plasma particles on a river surface through collisions, i.e. That is, thermodynamic quantities can be assigned to them on the river surface, e.g. B. a common temperature and density and thus a common pressure. The left part of the figure shows such a river area with some marked field lines. In the case of a stellarator shown, this flow surface has a three-dimensional structure; in the case of a tokamak, it would be continuously rotationally symmetrical about the axis of the torus . On the right and below, cross sections (Poincaré plots) are shown, which represent the intersection points of field lines through a poloidal cross section. One recognizes the nested structure of the closed river areas in the containment area. On the right of the picture is the calculated Poincaré plot for a poloidal plane with a banana-shaped cross-section in a magnetic configuration of the Wendelstein 7-X . In the graphic below you can see the measured flow areas of the Wendelstein 7-AS : The intersection points of the field lines through a plane with - at this point - a more triangular cross-section are made visible by a fluorescent medium in the plane. Points shown in false colors green and brown were measured before and after over 50,000 plasma experiments carried out over the course of 14 years and show that the modular coil arrangement was not changed by these loads.
In general, a plasma particle comes arbitrarily close to any point on the flow surface as it moves. Exceptions are river areas on which the twisting ( rotation transformation ) leads to the field lines closing in on themselves after a few revolutions. Such “rational flow areas” are sensitive to minor magnetic field disturbances, which can lead to island-like magnetic field structures, as they are marked in the illustration on the right at the edge of the containment area. Such fixed or dynamically developing islands represent weak points or holes in this magnetic cage and can lead to a loss of the plasma.
The magnetic fields for the plasma containment require strong currents (of the order of 20 kA) in large coils. The current strength determines the achievable plasma pressure. A plasma pressure of several bar would have to be achieved in a power plant ; this can be achieved with coils made of suitable superconductors .
Some newer configurations of toroidal machines are the "Reversed Field Pinch" and the "Floating Dipole Experiment".
Compact tori
Compact tori, e.g. B. the Spheromak and the FRC (Field-Reversed Configuration) try to combine the good containment properties of closed magnetic surfaces with the simplicity of machines without a central coil.
Lawson criterion not met
The plasma physics development work basically pursues the goal of approaching the Lawson criterion . Stacey figuratively calls this the “holy grail” of plasma research; a plasma would “burn” in this state without any external energy supply.
When trying to increase the particle density, temperature and energy containment time of the plasma accordingly, all of the concepts mentioned run into difficulties. Sometimes magnetic confinement is compared to trying to squeeze a balloon evenly - the air will repeatedly evert the balloon in new places. Such instabilities play an important role because they can cause the plasma to break out of the confinement area and come into contact with the vessel wall. When this happens, heavy particles (eg., Carbon or iron) from the wall of the vessel (steel or other metals) dissolved out ( " sputtering " or sputtering) mix with the plasma and set its temperature above the emission of braking radiation down . Turbulence plays a very important role : it leads to the transport of particles and energy out of the plasma, which reduces the energy containment time.
Considerable progress has been made since the 1990s, both in bringing the three values involved for particle density, temperature and energy inclusion time closer to those required for “burning” plasmas and in the scientific understanding of the processes involved. In JET experiments, up to 16 megawatts of fusion power could be achieved for a short time and the behavior of the helium nuclei (alpha particles) in weakly burning plasmas could be investigated.
Electromagnetic waves can be injected into the plasma and used to affect the trajectories of plasma particles and drive currents that create magnetic fields confining the plasma. These and other findings and advances in plasma research were largely obtained through experiments on tokamaks.
Fusion with net energy gain without reaching the Lawson criterion
The Lawson condition is necessary for nuclear weapons and inertial fusion reactors to function. In the case of the magnetic confinement concept, it does not have to be fulfilled, because here it is possible to continue to heat the plasma while it supplies fusion energy. For a net energy gain it is only necessary that the usable fusion power exceeds the supplied heating power; this is sometimes referred to in the literature as scientific break-even for other inclusion methods . This case is to be implemented for the first time with ITER. The fusion power can be related to the additional heating power in the sense of a gain factor:
- .
The Lawson criterion fulfilled would correspond . In the facility JET was reached in 1997 . is the aforementioned scientific break-even . The next “milestone” on this development path would be engineering break-even , i.e. a merger that exceeds the power plant's entire self-consumption, including cooling, etc. That which is necessary for an overall economical energy generation should be beyond 10.
ITER is designed for the value ≈ 10. Much higher values cannot be achieved with the technology from ITER, because the heating systems there are also necessary to control the inherently unstable plasma.
Even later power reactors will probably be designed in such a way that the Lawson criterion is not met, but rather a weak additional heating of, for example, a few percent of the fusion power remains necessary in order to retain an additional control option.
literature
- Friedrich Wagner : On the way to the fusion power plant - organized and self-organizing magnetic confinement . Physik Journal 8 (2009), No. 8/9, pp. 35-41
- Weston M. Stacey: Fusion. An Introduction to the Physics and Technology of Magnetic Confinement Fusion. Wiley-VCH, 2010, ISBN 978-3-527-40967-9 , limited preview in Google Book Search.
- CM Braams and PE Stott: Nuclear Fusion. Half a Century of Magnetic Confinement Fusion Research . IOP Publishing, Bristol 2002, ISBN 0-7503-0705-6 .
Web links
- EFDA-JET web site
- Culham Center for Fusion Energy, CCFE
- Max Planck Institute for Plasma Physics
- Physics of magnetically confined plasmas (PDF; 2.1 MB)
- " General Atomics operates the San Diego-based DIII-D facility "
swell
- ^ Resonator podcast of the Helmholtz Association : Tokamak and Stellarator (episode 30, April 25, 2015)
- ↑ http://www.ipp.mpg.de/de/aktuelles/presse/pi/2015/12_15
- ↑ M. Otte, R. Jaenicke: Magnetic flux surface measurements at Wendelstein W7-AS. (pdf; 3.2 MB) (No longer available online.) In: Stellarator News - Issue 100 . James A. Rome at Oak Ridge National Laboratory, September 2005, pp. 2-5 , archived from the original on July 14, 2016 ; accessed on July 14, 2016 . Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.
- ↑ Dennis Whyte et al. ( MIT ): Smaller & Sooner: How a new generation of superconductors can accelerate fusion's development . Fusion Power Associates 2012, 31st Annual Meeting and Symposium, Washington, DC, December 2012.
- ↑ a b c Stacey, Fusion (see literature list), page 9
- ↑ M. Keilhacker, JET Deuterium-Tritium Results and their Implications, website of EUROfusion. Retrieved August 16, 2016.
- ↑ JS Brzosko ei al .: Comments on the feasibility of achieving scientific break-even with a plasma focus machine. In: E. Panarella (Ed.): Current trends in International Fusion Research , Plenum Press, 1997
- ↑ SA Slutz et a .: Subignition fusion yields generated by fast heating of compressed deuterium-tritium and break-even scaling. Physics of Plasmas Volume 11 (2004) page 3483, doi : 10.1063 / 1.1753574
- ↑ J. Hiwatari et al .: Plasma performance required for a tokamak reactor to generate net electric power. Journal of Plasma and Fusion Research Volume 78, No.10 (2002) page 991, [1]
- ^ J. Hiwatari et al .: Forthcoming Break-Even Conditions of Tokamak Plasma Performance for Fusion Energy Development. Journal of Plasma and Fusion Research Volume 81, No.11 (2006) pages 903-916, [2]






