Inversion (geometry)

Definition of the inversion on a circle or a sphere with center and radius : ${\displaystyle M}$ ${\displaystyle R}$
${\displaystyle |{\overline {MP'}}|\cdot |{\overline {MP}}|=R^{2}}$

In geometry, an inversion is either a reflection of a circle or a reflection on a sphere . Both terms are based on the usual reflection on a straight line in the plane or a plane in space and, like these, have the following properties:

a) There are many fixed points: the circle / sphere that is mirrored remains fixed point by point,

b) angles are retained (especially right angles),

c) Reflections are always involutor , d. i.e., they are identical to their inverse mapping.

However, there are essential differences: 1) An inversion mostly maps a straight line onto a circle. So it is not a collineation . 2) An inversion is not true to length.

Inversions have long played an important role in geometry. Inverse images of conic sections and quadrics in space are algebraic curves and surfaces of no more than 4th degree with interesting properties (see examples).

Definition and analytical description

An inversion on a circle or a sphere with a center point and radius maps one point from one point to another in such a way that ${\displaystyle M}$ ${\displaystyle R}$ ${\displaystyle M}$ ${\displaystyle P}$ ${\displaystyle P'}$

1. ${\displaystyle P'}$lies on the half-line and ${\displaystyle [MP}$
2. ${\displaystyle |{\overline {MP'}}|\cdot |{\overline {MP}}|=R^{2}}$ is.

The reflection on a circle with a radius whose center is at the origin of the coordinates can be passed through ${\displaystyle R}$

${\displaystyle (x,y)\mapsto {\frac {R^{2}\cdot (x,y)}{x^{2}+y^{2}}}}$

or the reflection on the sphere in space

${\displaystyle (x,y,z)\mapsto {\frac {R^{2}\cdot (x,y,z)}{x^{2}+y^{2}+z^{2}}}}$

describe.

In planar polar coordinates , a mirroring of a circle has a particularly simple representation: ${\displaystyle (r,\varphi )}$

${\displaystyle (r,\varphi )\mapsto \left({\frac {R^{2}}{r}},\varphi \right)}$.

The reflection on the unit circle is then

${\displaystyle (r,\varphi )\mapsto \left({\frac {1}{r}},\varphi \right)}$

and justifies the term inversion.

If the real plane is described in the usual way with complex numbers , the reflection on the unit circle can be seen in the figure

${\displaystyle z\mapsto {\frac {1}{\overline {z}}}}$

represent. (See also Möbius level .)

Properties of an inversion

A circular reflection has the following properties:

• Every point of the inversion circle is a fixed point .
• A straight line through the center M of the inversion circle is mapped onto itself. A straight line not through M merges into a circle through M. (see below)
• A circle through M is not mapped through M on a straight line. A circle not through M merges into a circle not through M. (see below)
• Angles are retained (a mirroring of a circle is a conformal image ). (see section generalization )
• An inversion is an involution , i. H. it is identical to its reverse image. She exchanges the inside of the inversion circle with the outside.

For the reflection on a sphere , replace the inversion "circle" with inversion "sphere" in the above properties and add the following properties:

• Planes through the origin are mapped onto themselves, other planes are mapped onto spheres through the origin. (see below)
• Balls that do not contain the origin are mapped to the same. Spheres through the origin transition to planes that do not contain the origin. (see below)

Inversions (circular reflections) of curves, examples

In the following, for the sake of simplicity, it is assumed that the inversion circle is the unit circle. The mapping rule then reads

• ${\displaystyle (x,y)\mapsto (X,Y)={\frac {(x,y)}{x^{2}+y^{2}}}\quad {\text{und}}\quad (X,Y)\mapsto (x,y)={\frac {(X,Y)}{X^{2}+Y^{2}}}\ .}$

If the parametric representation is a curve, then ${\displaystyle u\mapsto (x(u),y(u))}$

${\displaystyle u\mapsto (X(u),Y(u))={\frac {(x(u),y(u))}{x(u)^{2}+y(u)^{2}}}}$

a parametric representation of the image curve.

If a curve is an implicit representation, then ${\displaystyle f(x,y)=0}$

${\displaystyle f\left({\frac {X}{X^{2}+Y^{2}}},{\frac {Y}{X^{2}+Y^{2}}}\right)=0}$

an implicit representation of the image curve.

Inversion of a circle and two straight lines

Inversions of a parabola (left) and a hyperbola (right)

Inversion of a parabola, cardioids

Inversion of an ellipse

Example straight

The straight line with the equation is mapped onto the curve with the equation in accordance with the above mapping rule when mirroring the unit circle . This equation is equivalent to ${\displaystyle ax+by+c=0}$ ${\displaystyle a{\tfrac {X}{X^{2}+Y^{2}}}+b{\tfrac {Y}{X^{2}+Y^{2}}}+c=0}$

${\displaystyle aX+bY+c(X^{2}+Y^{2})=0}$

and describes in the case the original straight line, in the case a circle through the zero point with the equation ${\displaystyle c=0}$ ${\displaystyle c\neq 0}$

${\displaystyle \left(X+{\frac {a}{2c}}\right)^{2}+\left(Y+{\frac {b}{2c}}\right)^{2}={\frac {a^{2}+b^{2}}{4c^{2}}}\ .}$

In the following examples, for the sake of simplicity, the (small) ones are also used for the image curve. ${\displaystyle X,Y}$ ${\displaystyle x,y}$

Example circle

The circle with the equation is mapped onto the curve with the equation according to the above mapping rule when mirroring the unit circle . This equation is equivalent to ${\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}=r^{2}}$ ${\displaystyle ({\tfrac {x}{x^{2}+y^{2}}}-x_{0})^{2}+({\tfrac {y}{x^{2}+y^{2}}}-y_{0})^{2}=r^{2}}$

${\displaystyle (x^{2}+y^{2})(x_{0}^{2}+y_{0}^{2}-r^{2})-2xx_{0}-2yy_{0}+1=0}$

and
in the case (the original image circle goes through the zero point) describes the straight line ${\displaystyle x_{0}^{2}+y_{0}^{2}=r^{2}}$

${\displaystyle 2xx_{0}+2yy_{0}=1\ .}$

If is, the above equation can be transformed ${\displaystyle x_{0}^{2}+y_{0}^{2}\neq r^{2}}$

${\displaystyle \left(x-{\frac {x_{0}}{x_{0}^{2}+y_{0}^{2}-r^{2}}}\right)^{2}+\left(y-{\frac {y_{0}}{x_{0}^{2}+y_{0}^{2}-r^{2}}}\right)^{2}={\frac {r^{2}}{(x_{0}^{2}+y_{0}^{2}-r^{2})^{2}}}\ .}$

This equation describes a circle.
If is, there is again a circle with the zero point as the center and radius ${\displaystyle x_{0}=y_{0}=0}$ ${\displaystyle 1/r\ .}$

Example parabola

a) The parabola is mapped onto the curve as a parameterized curve (by reflection on the unit circle) (see picture). The implicit curve for the image curve is the equation , this is the equation of a zissoid . ${\displaystyle y=x^{2}}$ ${\displaystyle (u,u^{2})}$ ${\displaystyle ({\tfrac {1}{u(1+u^{2})}},{\tfrac {1}{1+u^{2}}})}$ ${\displaystyle x^{2}-y=0}$ ${\displaystyle x^{2}-y(x^{2}+y^{2})=0}$

b) The parabola is mapped onto the cardioids with the equation by mirroring the circle . The inversion of a parabola results in a cardioid only if the inversion center is in focus. ${\displaystyle y=x^{2}-{\tfrac {1}{4}}}$ ${\displaystyle (x^{2}+y^{2}+2y)^{2}=4(x^{2}+y^{2})}$

In the inversion of a parabola, the tangents merge into a family of circles through the zero point, the envelope of which is the image curve. In the case of the cardioids, the centers of these circles also lie on a circle through the zero point (in example b) this circle has the radius 1). This property is used to draw a cardioid as the envelope of circles: 1) Choose a circle k and a point O on it, 2) Draw circles through O with centers on k, 3) Draw the envelope of these circles.

Example hyperbola

a) The hyperbola with the equation is mapped onto the lemniscate with the equation through the reflection at the unit circle (see picture). ${\displaystyle x^{2}-y^{2}=1}$ ${\displaystyle (x^{2}+y^{2})^{2}-(x^{2}-y^{2})=0}$

b) The inversion of the hyperbola results in the Cartesian leaf (see picture). ${\displaystyle (x-1)^{2}-y^{2}=1}$ ${\displaystyle x^{2}-2x(x^{2}+y^{2})-y^{2}=0}$

Circular reflection on the Riemann number sphere

Circular reflection on the Riemann sphere: the points M, P, P 'correspond to the points m, p, p' (magenta) on the sphere

If one considers such an assignment of the real plane to points of the Riemann number sphere , that

1. the real plane the equatorial plane and
2. the unit circle corresponds to the equator circle,

so the reflection on the unit circle is conveyed as an image on the Riemann number sphere by the usual reflection on the equatorial plane (see picture). Here, the point is the point reversed and circles by going in circles through over. Circles through correspond to straight lines in the plane model. ${\displaystyle N}$ ${\displaystyle m}$ ${\displaystyle N}$ ${\displaystyle m}$ ${\displaystyle N=\infty }$

Information on the visualization of implicit curves can be found here .

Inversion (spherical reflection) of planes, spheres, straight lines and circles

Analogous to the circular reflection (see above) one shows mathematically that a

• Plane on a plane or sphere (through the origin) and
• Sphere on a plane (if the sphere goes through the zero point) or sphere

is mapped.

Since a straight line in space can be understood as the intersection of two planes, a straight line changes into the intersection of two planes or the intersection of a plane and a sphere or the intersection of two spheres. I.e.

• The image of a straight line is either a straight line or a circle.

Since a circle can be understood as the intersection of a plane and a sphere, a circle changes into the intersection of a plane and a sphere or the intersection of two planes or the intersection of two spheres. I.e.

• The image of a circle is either again a circle or a straight line.
• A spherical reflection is conformal . (See section Generalization .)

Inversions of surfaces, examples

Inversion of a sphere

Inversion of an ellipsoid

Inversion of a single-shell hyperboloid

Surface inversions provide the ability to create surfaces with predictable properties. Since circles and spheres that do not go through the origin (the inversion center) are mapped onto the same again, simple areas that contain many circles or are channel areas are mapped by an inversion. For example, the inverse surfaces of perpendicular circular cylinders, perpendicular circular cones and rotational gates are precisely the Dupin's cyclids .

Parametric representations or implicit representations result analogously to the curve case (see above).

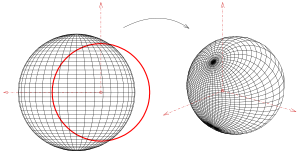
Example sphere with longitude and latitude

The simplest surface for an inversion is a sphere with circles of longitude and latitude. The image of the sphere is again a sphere and the circles of longitude and latitude merge into a system of orthogonally intersecting circles. However, the images of the north and south poles are generally no longer on a sphere diameter (see picture).

Example ellipsoid with circles and ellipses

On an ellipsoid of revolution lies a family of horizontal circles, which in the example shown in the picture are again mapped onto circles. The vertical ellipses of the ellipsoid are mapped to curves that are similar to the above example of a circular mirroring of an ellipse.

Example of a single-shell hyperboloid with circles and hyperbolas

On a single-shell rotational hyperboloid lies a family of circles (in the picture there are horizontal circles) and two families of straight lines (in the picture a straight line (blue) is shown). The circles merge again into a family of circles covering the surface. Also every straight line (generating line) of the hyperboloid merges into a circle through the origin (see picture). The family of hyperbolas (they intersect the circles orthogonally) is mapped onto a family of lemniscate-like curves that contain the origin. Only these parts of these curves are shown in the picture, which result as images of the hyperbolic arcs.

Information on the visualization of implicit areas can be found here .

Stereographic projection as the inversion of a sphere

Stereographic projection of a square network (in the plane)

Stereographic projection as inversion

In the case of stereographic projection , the points of a sphere are projected from a point on the sphere onto the tangential plane of the opposite point (see picture). This mapping can be understood as the inversion of a sphere on a plane. If the sphere that is mapped has the equation (center point , radius , green in the picture), it is mapped to the tangential plane in the point during the inversion on the unit sphere (red in the picture) . The straight lines through the inversion center are mapped onto themselves. They are the projection rays of the stereographic projection. The longitudinal circles of the sphere that are visible in the picture are mapped through S on straight lines (the tangential plane in the south pole S). The circles of latitude merge into concentric circles with a center point S. ${\displaystyle N}$ ${\displaystyle S}$ ${\displaystyle x^{2}+y^{2}+(z+{\tfrac {1}{2}})^{2}={\tfrac {1}{4}}}$ ${\displaystyle (0,0,-0{,}5)}$ ${\displaystyle 0{,}5}$ ${\displaystyle S=(0,0,-1)}$ ${\displaystyle N}$

Example square network: The second image for stereographic projection shows the projection of a flat square network in the tangential plane of the south pole onto the sphere. Since straight lines of the plane are mapped to circles through the north pole, the network creates two families of such circles, each with the same tangent in the north pole. Since an inversion and thus also a stereographic projection is angularly true (see below), the circles touch each other (in N) or intersect perpendicularly in N and another point.

generalization

Analogous to the 2-dimensional case, the concept of inversion can be transferred to an n-dimensional Euclidean space and analyzed analytically

• ${\displaystyle {\vec {x}}\mapsto {\frac {R^{2}\cdot {\vec {x}}}{|{\vec {x}}|^{2}}}}$

describe.

Images of hyperplanes and hyperspheres

As with the proof that a mirroring of a circle maps straight lines and circles into the same, one shows with the help of vector calculation that in the general case applies:

• In the event of an inversion, hyperplanes and hyperspheres merge into the same.

Conformity

Let it be a regular curve im and the inverse curve with respect to the reflection at the unit hypersphere. Then applies ${\displaystyle {\vec {x}}={\vec {c}}\;(s)}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle {\vec {x}}={\vec {\gamma }}\;(s)={\tfrac {{\vec {c}}\;(s)}{{\vec {c}}\;^{2}(s)}}}$

${\displaystyle {\vec {\gamma }}\;'={\frac {{\vec {c}}\;'{\vec {c}}\;^{2}-2{\vec {c}}({\vec {c}}\cdot {\vec {c}}\;')}{({\vec {c}}\;^{2})^{2}}}\ .}$(The argument was omitted in each case.) ${\displaystyle (s)}$

Similarly, for another regular curve and its inverse  : ${\displaystyle {\vec {x}}={\vec {d}}(t)}$ ${\displaystyle {\vec {x}}={\vec {\delta }}(t)={\tfrac {{\vec {d}}(t)}{{\vec {d}}\;^{2}(t)}}}$

${\displaystyle {\vec {\delta }}\;'={\frac {{\vec {d}}\;'{\vec {d}}\;^{2}-2{\vec {d}}({\vec {d}}\cdot {\vec {d}}\;')}{({\vec {d}}\;^{2})^{2}}}\ .}$

Both curves may be parameterized according to the arc length (i.e. it is ) and intersect at the point . Then their inverses cut into . At these points of intersection, the above formulas apply and one calculates that ${\displaystyle |{\vec {c}}\;'|=|{\vec {d}}\;'|=1}$ ${\displaystyle {\vec {c}}(0)={\vec {d}}(0)}$ ${\displaystyle {\vec {\gamma }}(0)={\vec {\delta }}(0)}$ ${\displaystyle {\vec {c}}={\vec {d}}\ }$

${\displaystyle ({\vec {\gamma }}\;')^{2}=\dots ={\frac {1}{({\vec {c}}\;^{2})^{2}}}=({\vec {\delta }}\;')^{2}\ .}$

Taking into account that is, the following results for the intersection angle of the image curves: ${\displaystyle {\vec {c}}={\vec {d}}\ }$ ${\displaystyle \alpha }$

• ${\displaystyle \cos \alpha ={\frac {{\vec {\gamma }}\;'}{|{\vec {\gamma }}\;'|}}\cdot {\frac {{\vec {\delta }}\;'}{|{\vec {\delta }}\;'|}}=({\vec {\gamma }}\;'\cdot {\vec {\delta }}\;')\;({\vec {c}}\;^{2})^{2}=\dots ={\vec {c}}\;'\cdot {\vec {d}}\;'\ .}$

So the angle of intersection of the inverse curves is identical to the angle of intersection of the given curves.

literature

• W. Blaschke : Lectures on Differential Geometry I . 1921, Springer-Verlag, ISBN 978-3-642-49388-1 , p. 66.
• F. Borges: The reflection in the circle. Books on Demand , Norderstedt, 2015, ISBN 978-3-7347-9186-4 .
• R. Courant , H. Robbins: What is Mathematics? Springer-Verlag, 1967, ISBN 978-3-662-00054-0 , p. 125.
• L. Felix: Elementary mathematics in a modern representation. Vieweg-Verlag, 1969, ISBN 978-3-322-96093-1 , p. 482.
• K. Fladt : Analytical geometry of special surfaces and space curves. Vieweg-Teubner-Verlag, ISBN 978-3-528-08278-9 , p. 201.
• T. Needham: Descriptive Function Theory. Oldenbourg-Verlag, 2001, ISBN 3-486-24578-3 , p. 144.
• H. Schmidt: The inversion and its applications , 1950, Oldenbourg-Verlag.

Web links

• Circular reflection. GeoGebra applet
• inverse . 2dcurves
• Eric W. Weisstein : Inverse Curve . In: MathWorld (English).
• Inversion . In: Visual Dictionary Of Special Plane Curves
• Inverse d'une courbe by rapport à un point . In: Encyclopédie des Formes Mathématiques Remarquables