List of inertia tensors

The inertia tensor (symbol , dimension M L², SI unit kg m² ) of a rigid body indicates its moments of inertia , i.e. the body's resistance to accelerated rotations. The inertia tensor plays a comparable role for rotations as does the mass for translational movements . It must not be confused with the geometrical moment of inertia that is used in beam bends. ${\displaystyle \mathbf {I} ,\mathbf {\Theta } ,I}$

The calculation of the inertia tensor of real bodies requires the evaluation of volume integrals , which is correspondingly complex. The determination is easier if the body is made up of parts whose inertia tensor is known. With the rule for the tensor transformation for rotations and Steiner's theorem, the inertia tensor of the body can then be determined without integrations. For this purpose, the inertial tensors of some simple bodies with homogeneous mass distribution are listed in the tables below.

Calculation of inertia tensors

The table shows the inertia tensors with respect to the origin of a Cartesian coordinate system with a standard base , which here - unless otherwise specified - coincides with the main axis system. If the center of mass of the body is at the origin, the inertia tensor is denoted by I _s , otherwise by I ₀ , and has the representations ${\displaystyle {\hat {e}}_{x,y,z}}$

${\displaystyle \mathbf {I} _{0}:={\begin{pmatrix}I_{x}\\&I_{y}\\&&I_{z}\end{pmatrix}}:=I_{x}{\hat {e}}_{x}\otimes {\hat {e}}_{x}+I_{y}{\hat {e}}_{y}\otimes {\hat {e}}_{y}+I_{z}{\hat {e}}_{z}\otimes {\hat {e}}_{z}:=\int _{V}[({\vec {x}}\cdot {\vec {x}})\mathbf {1} -{\vec {x}}\otimes {\vec {x}}]\;\rho \mathrm {d} V}$

In it is

• V is the volume of the body,
• ρ is the density,
• I _{x, y, z} main moment of inertia,
• ${\displaystyle {\vec {x}}=x{\hat {e}}_{x}+y{\hat {e}}_{y}+z{\hat {e}}_{z}}$the position vector with x, y and z coordinates,
• ⊗ the dyadic product and
• 1 is the unit tensor .

If there is another right-handed orthonormal basis , then is ${\displaystyle {\hat {g}}_{x,y,z}}$

${\displaystyle \mathbf {J} :=I_{x}{\hat {g}}_{x}\otimes {\hat {g}}_{x}+I_{y}{\hat {g}}_{y}\otimes {\hat {g}}_{y}+I_{z}{\hat {g}}_{z}\otimes {\hat {g}}_{z}=\mathbf {Q\cdot I\cdot Q} ^{\top }}$

the inertia tensor with principal axis system . In it is ${\displaystyle {\hat {g}}_{x,y,z}}$

${\displaystyle \mathbf {Q} :={\hat {g}}_{x}\otimes {\hat {e}}_{x}+{\hat {g}}_{y}\otimes {\hat {e}}_{y}+{\hat {g}}_{z}\otimes {\hat {e}}_{z}={\begin{pmatrix}{\hat {g}}_{x}&{\hat {g}}_{y}&{\hat {g}}_{z}\end{pmatrix}}}$

an orthogonal tensor . In the last illustration, the basis vectors were set as column vectors. With Steiner's theorem, the inertia tensor can be calculated with respect to any other reference point:

${\displaystyle \mathbf {I} _{c}=\mathbf {I} _{s}+m[({\vec {c}}\cdot {\vec {c}})\mathbf {1} -{\vec {c}}\otimes {\vec {c}}]}$

Therein is the distance vector from the center of mass s , which was used for the calculation of I _s . In particular is here ${\displaystyle {\vec {c}}}$

${\displaystyle \mathbf {I} _{0}=\mathbf {I} _{s}+m[({\vec {s}}\cdot {\vec {s}})\mathbf {1} -{\vec {s}}\otimes {\vec {s}}]}$

if the center of mass is not in the origin. ${\displaystyle {\vec {s}}}$

The inertia tensors of two sub-bodies can be added if they are set up with respect to the same reference point. Inertia tensors can also be subtracted if the volume of the corresponding part of the body is to be left out.

Point mass

A point mass has no moments of inertia with respect to the axes on which it lies. According to Steiner's theorem, however, it causes moments of inertia if it is not on the axis of rotation.

description	image	Inertia tensor
Point mass m at x = r .		${\displaystyle \mathbf {I} _{0}={\begin{pmatrix}0\\&mr^{2}\\&&mr^{2}\end{pmatrix}}}$
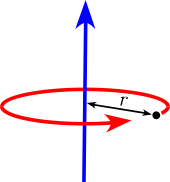
Two point masses M and m at a distance a on the x-axis and center of mass at x = 0.		${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}0\\&{\frac {Mm}{M+m}}a^{2}\\&&{\frac {Mm}{M+m}}a^{2}\end{pmatrix}}}$

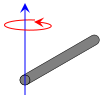
Bar, parallelogram and cuboid

description	image	Inertia tensor
Slender bar in x-direction with length l and mass m with respect to one end.		${\displaystyle \mathbf {I} _{0}={\begin{pmatrix}0&&\\&{\frac {m}{3}}l^{2}&\\&&{\frac {m}{3}}l^{2}\end{pmatrix}}}$
Slender bar in x-direction with length l and mass m with respect to its center. This inertia tensor arises in the massive cuboid below with b = h = 0.		${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}0&&\\&{\frac {m}{12}}l^{2}&\\&&{\frac {m}{12}}l^{2}\end{pmatrix}}}$
Thin rectangular plate in the xy-plane with length w in x-direction, width h in y-direction and mass m . This inertia tensor arises for the massive cuboid below with h = 0.		${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}{\frac {m}{12}}h^{2}&&\\&{\frac {m}{12}}w^{2}&\\&&{\frac {m}{12}}(w^{2}+h^{2})\end{pmatrix}}}$
Thin parallelogram -shaped plate with side L , height h , "overhang" p and ground m . With p = 0 the rectangular plate is created. Only there are the main axes of inertia parallel to the selected coordinate axes.		${\displaystyle \mathbf {I} _{s}={\frac {m}{12}}{\begin{pmatrix}h^{2}&-hp&\\-hp&l^{2}+p^{2}&\\&&h^{2}+l^{2}+p^{2}\end{pmatrix}}}$
Solid cuboid with length l in x-direction, width b in y-direction, height h in z-direction and mass m . The inertia tensors of thin plates or slender rods are created by setting one or two dimensions b, h or t to zero .		${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}{\frac {m}{12}}(b^{2}+h^{2})&&\\&{\frac {m}{12}}(l^{2}+h^{2})&\\&&{\frac {m}{12}}(l^{2}+b^{2})\end{pmatrix}}}$

1. ↑ ^{a b c d e} The axis of rotation is - unlike in the picture - arbitrary.

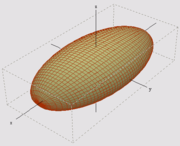
Disc, torus and sphere

description	image	Inertia tensor
Thin circular ring with radius r and mass m . This is the special case of the torus with a = 0 and the cylindrical tube with open ends with r 1 = r 2 and h = 0.		${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}{\frac {m}{2}}r^{2}\\&{\frac {m}{2}}r^{2}\\&&mr^{2}\end{pmatrix}}}$
Thin disk with radius r and mass m . This is the special case of a massive cylinder with h = 0.		${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}{\frac {m}{4}}r^{2}\\&{\frac {m}{4}}r^{2}\\&&{\frac {m}{2}}r^{2}\end{pmatrix}}}$
Torus with a large circle in the xy plane and radius b , radius of the small circle a and mass m .		${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}{\frac {m}{8}}(5a^{2}+4b^{2})\\&{\frac {m}{8}}(5a^{2}+4b^{2})\\&&{\frac {m}{4}}(3a^{2}+4b^{2})\end{pmatrix}}}$
Sphere with radius r and mass m .		${\displaystyle {\begin{aligned}\mathbf {I} _{\rm {s,d{\ddot {u}}nnwandig}}=&{\frac {2m}{3}}r^{2}\mathbf {1} \\\mathbf {I} _{\rm {s,massiv}}=&{\frac {2m}{5}}r^{2}\mathbf {1} \end{aligned}}}$
Thick-walled sphere with outer radius r 2 and a central spherical cavity with radius r 1 and mass m . With the inner radius r 1 = 0, the special case of the massive sphere arises. From r 1 = r 2 arises because of the special case of the thin-walled sphere. ${\displaystyle \lim \limits _{r_{1}\to r_{2}}{\frac {{r_{2}}^{5}-{r_{1}}^{5}}{{r_{2}}^{3}-{r_{1}}^{3}}}={\frac {5}{3}}r_{2}^{2}}$		${\displaystyle \mathbf {I} _{s}={\frac {2m}{5}}\left({\frac {{r_{2}}^{5}-{r_{1}}^{5}}{{r_{2}}^{3}-{r_{1}}^{3}}}\right)\mathbf {1} }$
Solid ellipsoid with semi-axes a , b , c in x, y or z direction and mass m . With a = b = c a massive sphere with radius a is created .		${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}{\frac {m}{5}}(b^{2}+c^{2})&&\\&{\frac {m}{5}}(a^{2}+c^{2})&\\&&{\frac {m}{5}}(a^{2}+b^{2})\end{pmatrix}}}$

Triangular disk and pyramid

description	image	Inertia tensor
Thin triangular disk with height h , base l = p + q ′ and mass m . Only with symmetry with p = q are the main axes of inertia parallel to the selected coordinate axes.		${\displaystyle \mathbf {I} _{s}={\frac {m}{36}}{\begin{pmatrix}2h^{2}&(q-p)h\\(q-p)h&2(l^{2}-pq)\\&&2(h^{2}+l^{2}-pq)\end{pmatrix}}}$
Rectangular pyramid with height h , width a in x-direction, width b in y-direction and mass m with respect to the center of gravity S.		${\displaystyle \mathbf {I} _{s}={\frac {m}{80}}{\begin{pmatrix}4b^{2}+3h^{2}\\&4a^{2}+3h^{2}&\\&&4a^{2}+4b^{2}\end{pmatrix}}}$
Rectangular pyramid with height h , width a in x-direction, width b in y-direction and mass m with respect to the tip O.		${\displaystyle \mathbf {I} _{O}={\frac {m}{20}}{\begin{pmatrix}b^{2}+12h^{2}\\&a^{2}+12h^{2}&\\&&a^{2}+b^{2}\end{pmatrix}}}$

cone

description	image	Inertia tensor
Straight solid circular cone with radius r , height h and mass m with respect to its center of gravity.		${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}{\frac {3m}{80}}(4r^{2}+h^{2})&&\\&{\frac {3m}{80}}(4r^{2}+h^{2})&\\&&{\frac {3m}{10}}r^{2}\end{pmatrix}}}$
Right circular cone with radius r , height h and mass m with respect to its tip.		${\displaystyle {\begin{aligned}\mathbf {I} _{\rm {0,massiv}}=&{\begin{pmatrix}{\frac {3m}{20}}(r^{2}+4h^{2})&&\\&{\frac {3m}{20}}(r^{2}+4h^{2})&\\&&{\frac {3m}{10}}r^{2}\end{pmatrix}}\\\mathbf {I} _{\rm {0,d{\ddot {u}}nnwandig}}=&{\begin{pmatrix}{\frac {m}{4}}\left(r^{2}+2h^{2}\right)&&\\&{\frac {m}{4}}\left(r^{2}+2h^{2}\right)&\\&&{\frac {m}{2}}r^{2}\end{pmatrix}}\end{aligned}}}$

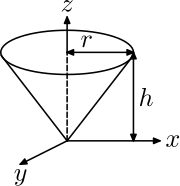
Tube and cylinder

description	image	Inertia tensor
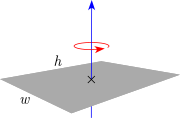
Solid cylinder with radius r , height h and mass m		${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}{\frac {m}{12}}(3r^{2}+h^{2})&&\\&{\frac {m}{12}}(3r^{2}+h^{2})&\\&&{\frac {m}{2}}r^{2}\end{pmatrix}}}$
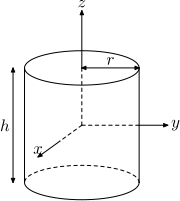
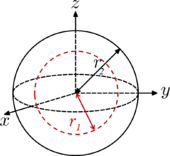
Thick-walled cylindrical tube with open ends, inner radius r 1 , outer radius r 2 , length h and mass m		${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}{\frac {m}{12}}(3({r_{1}}^{2}+{r_{2}}^{2})+h^{2})&&\\&{\frac {m}{12}}(3({r_{1}}^{2}+{r_{2}}^{2})+h^{2})&\\&&{\frac {m}{2}}({r_{1}}^{2}+{r_{2}}^{2})\end{pmatrix}}}$

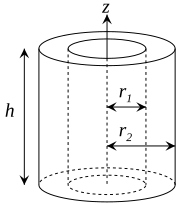
Any rotationally symmetrical body

The calculation of the inertia tensor with volume integrals can be at rotating bodies with the inertia tensor for the thin circular disk and simplify the Steiner's theorem, because then the body of can (infinitesimal) thin circular disks are thought put together.

The material of the body has the density ρ , its figure axis lies in the z-direction and the generating curve is given by the radius r ( z ). The mass of the circular disks with thickness t is at the point z

${\displaystyle m(z,t)=\rho \pi r^{2}(z)t}$

The circular disk has the inertia tensor around its center at z

${\displaystyle \mathbf {I} _{s}={\begin{pmatrix}{\frac {m(z,t)}{4}}r^{2}(z)\\&{\frac {m(z,t)}{4}}r^{2}(z)\\&&{\frac {m(z,t)}{2}}r^{2}(z)\end{pmatrix}}={\frac {\rho \pi }{4}}r^{4}(z)t{\begin{pmatrix}1\\&1\\&&2\end{pmatrix}}}$

With regard to the origin, there is still Steiner's part

${\displaystyle \mathbf {I} _{z}=m(z,t)z^{2}{\begin{pmatrix}1\\&1\\&&0\end{pmatrix}}=\rho \pi r^{2}(z)z^{2}t{\begin{pmatrix}1\\&1\\&&0\end{pmatrix}}}$

added. Thus the inertia tensor arises from the integral

${\displaystyle {\begin{aligned}\mathbf {I} _{0}=&{\frac {\rho \pi }{4}}\int _{z_{1}}^{z_{2}}r^{4}(z)\mathrm {d} z{\begin{pmatrix}1\\&1\\&&2\end{pmatrix}}+\rho \pi \int _{z_{1}}^{z_{2}}r^{2}(z)z^{2}\mathrm {d} z{\begin{pmatrix}1\\&1\\&&0\end{pmatrix}}\\=&{\frac {\rho \pi }{4}}\int _{z_{1}}^{z_{2}}{\begin{pmatrix}r^{4}(z)+4r^{2}(z)z^{2}\\&r^{4}(z)+4r^{2}(z)z^{2}\\&&2r^{4}(z)\end{pmatrix}}\mathrm {d} z\end{aligned}}}$

over circular disks of thickness d z .

The inertia tensor for the straight circular cone with radius r and height h with respect to its center of mass arises with in the interval [-¼ h, ¾ h] and its mass . ${\displaystyle r(z)=\left({\tfrac {3}{4}}-{\tfrac {z}{h}}\right)r}$ ${\displaystyle m={\tfrac {\rho \pi }{3}}r^{2}h}$

Platonic solids

With the Platonic solids the three main moments of inertia are the same.

description	image	Inertia tensor (diagonal element)
Regular tetrahedron with edge length s and mass m .		${\displaystyle {\begin{aligned}I_{\rm {s,d{\ddot {u}}nnwandig}}=&{\frac {m}{12}}s^{2}\mathbf {1} \\I_{\rm {s,massiv}}=&{\frac {m}{20}}s^{2}\mathbf {1} \end{aligned}}}$
Regular octahedron with edge length s and mass m .		${\displaystyle {\begin{aligned}\mathbf {I} _{\rm {s,d{\ddot {u}}nnwandig}}=&{\frac {m}{6}}s^{2}\mathbf {1} \\\mathbf {I} _{\rm {s,massiv}}=&{\frac {m}{10}}s^{2}\mathbf {1} \end{aligned}}}$
Regular dodecahedron with edge length s and mass m .		${\displaystyle {\begin{aligned}\mathbf {I} _{\rm {s,d{\ddot {u}}nnwandig}}=&{\frac {m}{90}}(39\phi +28)s^{2}\mathbf {1} \\\mathbf {I} _{\rm {s,massiv}}=&{\frac {m}{150}}(39\phi +28)s^{2}\mathbf {1} \end{aligned}}}$ in which ${\displaystyle \phi ={\frac {1+{\sqrt {5}}}{2}}}$
Regular icosahedron with edge length s and mass m .		${\displaystyle {\begin{aligned}\mathbf {I} _{\rm {s,d{\ddot {u}}nnwandig}}=&{\frac {m}{6}}\phi ^{2}s^{2}\mathbf {1} \\\mathbf {I} _{\rm {s,massiv}}=&{\frac {m}{10}}\phi ^{2}s^{2}\mathbf {1} \end{aligned}}}$ in which ${\displaystyle \phi ={\frac {1+{\sqrt {5}}}{2}}}$

example

The calculation of the inertia tensor of (asymmetrical) parallelograms, triangles and, from this, the tetrahedron will be demonstrated.

parallelogram

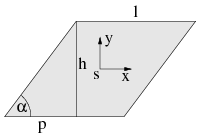
Parallelogram with center of mass at the origin.

The inertia tensor of a parallelogram can be calculated with the inertia tensors of members displaced in the x and y directions, see picture. A rod in the x-direction of length l, width b, thickness d and density ρ has the inertia tensor

${\displaystyle \mathbf {I} _{s}(b)={\frac {\rho dl^{3}}{12}}{\begin{pmatrix}0\\&1\\&&1\end{pmatrix}}b}$

If this is shifted to the center of gravity at (x _s , y _s ), the Steiner part is added

${\displaystyle {\begin{aligned}\mathbf {I} _{x}(b)=&\rho dl{\begin{pmatrix}0\\&{\frac {l^{2}}{12}}\\&&{\frac {l^{2}}{12}}\end{pmatrix}}b+\rho dl\left[(x_{s}^{2}+y_{s}^{2})\mathbf {1} -{\begin{pmatrix}x_{s}^{2}&x_{s}y_{s}\\x_{s}y_{s}&y_{s}^{2}\\&&0\end{pmatrix}}\right]b\\=&\rho dl{\begin{pmatrix}y_{s}^{2}&-x_{s}y_{s}\\-x_{s}y_{s}&{\frac {l^{2}}{12}}+x_{s}^{2}\\&&{\frac {l^{2}}{12}}+x_{s}^{2}+y_{s}^{2}\end{pmatrix}}b\end{aligned}}}$

With x _s = y _s cotα in the parallelogram it becomes:

${\displaystyle \mathbf {I} _{x}(b)=\rho dl{\begin{pmatrix}y_{s}^{2}&-y_{s}^{2}\cot \alpha \\-y_{s}^{2}\cot \alpha &{\frac {l^{2}}{12}}+y_{s}^{2}\cot ^{2}\alpha \\&&{\frac {l^{2}}{12}}+y_{s}^{2}(1+\cot ^{2}\alpha )\end{pmatrix}}b}$

Integration of this inertia tensor over the interval y _s ∈ [-½ h, ½ h] yields the inertia tensor of the parallelogram:

${\displaystyle \mathbf {I} _{p}=\int _{-h/2}^{h/2}\mathbf {I} _{x}(\mathrm {d} y)={\frac {\rho dhl}{12}}{\begin{pmatrix}h^{2}&-h^{2}\cot \alpha \\-h^{2}\cot \alpha &l^{2}+h^{2}\cot ^{2}\alpha \\&&l^{2}+h^{2}(1+\cot ^{2}\alpha )\end{pmatrix}}}$

With m = ρ dhl and p = h cotα the inertia tensor of a parallelogram reads:

${\displaystyle \mathbf {I} _{p}={\frac {m}{12}}{\begin{pmatrix}h^{2}&-hp&\\-hp&l^{2}+p^{2}&\\&&h^{2}+l^{2}+p^{2}\end{pmatrix}}}$

Only with p = 0 are the main axes parallel to the selected coordinate system and the inertia tensor of the rectangular plate is created.

triangle

Rectangle made up of two triangles

Division of the parallelogram along a diagonal into two triangles with mass m _d = ½ m _p yields their inertia tensor with respect to the origin:

${\displaystyle \mathbf {I} _{d0}={\frac {m_{d}}{12}}{\begin{pmatrix}h^{2}&-hp&\\-hp&l^{2}+p^{2}&\\&&h^{2}+l^{2}+p^{2}\end{pmatrix}}}$

The center of gravity of the triangle (yellow) is in the center of gravity of its corners:

${\displaystyle {\vec {s}}_{d}={\frac {1}{3}}({\vec {A}}+{\vec {B}}+{\vec {C}})={\frac {1}{3}}{\begin{pmatrix}-{\frac {q}{2}}-p+{\frac {q}{2}}-{\frac {q}{2}}\\-{\frac {h}{2}}-{\frac {h}{2}}+{\frac {h}{2}}\\0\end{pmatrix}}=-{\frac {1}{6}}{\begin{pmatrix}2p+q\\h\\0\end{pmatrix}}}$

When the center of gravity is shifted to the origin, the Steiner part is subtracted

${\displaystyle \mathbf {S} =m_{d}[({\vec {s}}_{d}\cdot {\vec {s}}_{d})\mathbf {1} -{\vec {s}}_{d}\otimes {\vec {s}}_{d}]={\frac {m_{d}}{36}}{\begin{pmatrix}h^{2}&-(2p+q)h\\-(2p+q)h&(2p+q)^{2}\\&&h^{2}+(2p+q)^{2}\end{pmatrix}}}$

from which the inertia tensor of a triangle arises:

${\displaystyle \mathbf {I} _{ds}=\mathbf {I} _{d0}-\mathbf {S} ={\frac {m_{d}}{36}}{\begin{pmatrix}2h^{2}&(q-p)h\\(q-p)h&2(l^{2}-pq)\\&&2(h^{2}+l^{2}-pq)\end{pmatrix}}}$

Only with symmetry with p = q are the main axes of inertia parallel to the selected coordinate axes.

The following special cases should be highlighted:

• Right triangles are created with pq = h² or p = 0 and q = l.
• Isosceles triangles have p = q = ½ l.
• Equilateral triangles result with p = q = ½ l and h² = ¾ l².

Tetrahedron

The inertia tensor of the regular tetrahedron can be calculated by breaking it down into equilateral triangular disks and adding up their inertia tensors. The mass of an equilateral triangular disk with density ρ, edge length l, height h and thickness d is . The inertia tensor reads: ${\displaystyle m_{d}={\frac {\rho }{2}}lhd={\frac {\sqrt {3}}{4}}\rho l^{2}d}$

${\displaystyle \mathbf {I} _{3s}(d)={\frac {m_{d}l^{2}}{24}}{\begin{pmatrix}1\\&1\\&&2\end{pmatrix}}={\frac {{\sqrt {3}}\rho }{96}}l^{4}{\begin{pmatrix}1\\&1\\&&2\end{pmatrix}}d}$

This triangular disk is shifted in the z-direction, which is due to the Steiner's part

${\displaystyle \mathbf {S} (d)=m_{d}z^{2}{\begin{pmatrix}1\\&1\\&&0\end{pmatrix}}}$

is to be considered. Taken together, the inertia tensor of the triangular disk at a distance z from the xy plane is:

${\displaystyle {\begin{aligned}\mathbf {I} _{3z}(d)=&\mathbf {I} _{3s}(d)+\mathbf {S} (d)={\frac {\sqrt {3}}{4}}\rho {\begin{pmatrix}{\frac {l^{4}}{24}}+l^{2}z^{2}\\&{\frac {l^{4}}{24}}+l^{2}z^{2}\\&&{\frac {l^{4}}{12}}\end{pmatrix}}d\end{aligned}}}$

The tetrahedron has the height and if the center of gravity is at the origin, then the base side is at and the opposite corner is at . This results in the edge length of the triangular disks at the height z: ${\displaystyle {\sqrt {\tfrac {2}{3}}}l}$ ${\displaystyle z_{0}=-{\tfrac {l}{\sqrt {24}}}}$ ${\displaystyle z_{1}={\sqrt {\tfrac {3}{8}}}l}$

${\displaystyle l(z)={\frac {z_{1}-z}{z_{1}-z_{0}}}l={\sqrt {\frac {3}{2}}}\left({\sqrt {\frac {3}{8}}}l-z\right)}$

With these definitions the inertia tensor of the tetrahedron is calculated:

${\displaystyle \mathbf {I} _{\triangle }={\frac {\sqrt {3}}{4}}\rho \int _{z_{0}}^{z_{1}}{\begin{pmatrix}{\frac {l^{4}(z)}{24}}+l^{2}(z)z^{2}\\&{\frac {l^{4}(z)}{24}}+l^{2}(z)z^{2}\\&&{\frac {l^{4}(z)}{12}}\end{pmatrix}}\mathrm {d} z={\frac {m_{\triangle }}{20}}l^{2}\mathbf {1} }$

where is its mass. ${\displaystyle m_{\triangle }=\rho {\frac {\sqrt {2}}{12}}l^{3}}$

literature

1. ↑ Eric W. Weisstein : Moment of Inertia - Ring. Wolfram Research , accessed December 14, 2016 . 
2. ↑ Raymond A. Serway: Physics for Scientists and Engineers . Saunders College Publishing, 1986, ISBN 0-03-004534-7 , pp. 202 .
3. ↑ Karl-Heinrich Grote, Jörg Feldhusen (Ed.): Dubbel . Paperback for mechanical engineering. Springer Vieweg Verlag, Berlin, Heidelberg 2014, ISBN 978-3-642-38891-0 , p. B31 , doi : 10.1007 / 978-3-642-38891-0 ( limited preview in Google Book Search [accessed January 13, 2018]).
4. ↑ Ferdin and P. Beer and E. Russell Johnston, Jr: Vector Mechanics for Engineers . McGraw-Hill, 1984, ISBN 0-07-004389-2 , pp. 911 .
5. ↑ ^{a b c d} John Satterly: The Moments of Inertia of Some Polyhedra . In: The Mathematical Gazette . tape 42 , no. 339 . Mathematical Association, 1958, pp. 11-13 , doi : 10.2307 / 3608345 .