Magnetohydrodynamics

The magnetohydrodynamics (MHD) is a branch of physics . It describes the behavior of electrically conductive fluids that are penetrated by magnetic (and electric ) fields.

Magnetohydrodynamics in the narrower sense deals with liquids, especially plasmas (magnetoplasm dynamics, MPD), which are described as liquids in the context of the MHD. Magnetogasdynamics (MGD), on the other hand, deals with gases.

The mathematical treatment is carried out by a combination of the Navier-Stokes equations of hydrodynamics with the Maxwell equations of electrodynamics .

Typical areas of application of MHD are flow control and flow measurement in metallurgy and semiconductor single crystal growth as well as the description of plasmas in stellar atmospheres and fusion reactors .

theory

In order to describe the dynamics of a plasma in detail, it would be necessary to solve the equation of motion for every particle. Of course, this approach is nonsensical because the number of particles is generally very large. In order to still be able to solve the problem, one chooses a statistical approach. In practice, this means that instead of looking at the trajectories of the individual particles, macroscopic values (mean values) are used.

An example of such a quantity is the flow velocity of a river. Overall, the river water moves in one direction towards the sea. Every single water molecule can move “back and forth” because it interacts continuously with other molecules. The only decisive factor for the macroscopic behavior is that the mean velocity corresponds to the flow velocity. With macroscopic quantities such as speed and pressure, all the phenomena of shipping can then be adequately described without a single molecule ever coming into play.

It is similar with the MHD. It too is basically a hydrodynamic theory in the sense that plasmas are treated in a similar way to liquids. Here, too, no individual particles, but rather “averaged sizes” are dealt with. The MHD combines elements of hydro- and electrodynamics to form a theory of "electrically conductive plasmas".

Usually a few more approximations are made. First, there is electrical neutrality, second, the validity of Ohm's law and third, quasi-equilibrium. The last approximation means that the plasma evolves, but slowly compared to the time it takes for equilibrium to be established. This assumption represents a great simplification for the equations, since it ensures, for example, that the pressure can be treated as a scalar quantity, while one is generally dealing with a (direction-dependent) tensor . The electrical neutrality eliminates the charge density from the equations. Under these conditions, the equations of the MHD can now be formulated.

The MHD equations

The basic equations of the MHD are (in CGS units ) as follows:

{\ displaystyle {\ begin {matrix} \ partial _ {t} \ rho + \ nabla \ cdot (\ rho \ mathbf {v}) & = & 0 & (1) \\ [2ex] \ rho \ partial _ {t} \ mathbf {v} + \ rho (\ mathbf {v} \ cdot \ nabla) \ mathbf {v} + \ nabla p & = & {\ dfrac {\ mathbf {J} \ times \ mathbf {B}} {c} } + \ rho \ mathbf {g} + \ mathbf {F} & (2) \\ [2ex] \ nabla \ times \ mathbf {B} & = & {\ dfrac {4 \ pi} {c}} \, \ mathbf {J} & (3) \\ [2ex] \ nabla \ times \ mathbf {E} & = & - {\ dfrac {1} {c}} \, \ partial _ {t} \ mathbf {B} & (4) \\ [2ex] \ nabla \ cdot \ mathbf {B} & = & 0 & (5) \\ [2ex] \ mathbf {J} & = & \ sigma \ left (\ mathbf {E} + {\ dfrac {\ mathbf {v} \ times \ mathbf {B}} {c}} \ right) \; & (6) & \ end {matrix}}}

The occurring quantities are the mass density , the plasma speed , the pressure , the electric current , the magnetic field , the electric field , the gravitational acceleration and the speed of light . In equation (2), gravity was explicitly taken into account; the term indicates that in general other forces such as B. Frictional forces must be taken into account that were not explicitly stated here. Equation (1) describes the conservation of mass, equation (2) is the "equation of motion" or "momentum equation", equations (3), (4) and (5) come from electrodynamics ( Maxwell's equations ), where in equation ( 3) the displacement current was neglected. Equation (6) is the Ohm's law to the electrical conductivity , . This is the only equation that takes relativistic effects into account. ${\ displaystyle \ rho}$ ${\ displaystyle \ mathbf {v}}$ ${\ displaystyle p}$ ${\ displaystyle \ mathbf {J}}$ ${\ displaystyle \ mathbf {B}}$ ${\ displaystyle \ mathbf {E}}$ ${\ displaystyle \ mathbf {g}}$ ${\ displaystyle c}$ ${\ displaystyle \ mathbf {F}}$ ${\ displaystyle \ sigma}$

To the system of equations to close, another equation is still needed. This can be, for example, the equation of state of matter or the equation of local energy conservation .

The MHD equations can be derived in different ways. One possibility is to start from the Boltzmann equation in order to arrive at the above result.

The induction equation

The so-called induction equation is obtained by combining the laws of Ampère , Faraday and Ohm (equations 3, 4 and 6) .

{\ displaystyle \ partial _ {t} \ mathbf {B} = \ nabla \ times (\ mathbf {v} \ times \ mathbf {B}) + \ eta \ Delta \ mathbf {B} \ ;.}

In the equation denotes the magnetic diffusivity. This equation plays an important role in understanding magnetic plasmas. ${\ displaystyle \ eta = c ^ {2} / (4 \ pi \ sigma) = 1 / (\ mu _ {0} \ sigma)}$

Ideal BBD

Solving the MHD equations can get very complicated. In many cases, however, further assumptions can be made to simplify the equations to make them easier to solve. If one assumes that the electrical conductivity of the plasma is infinitely large ( ), so it therefore has no electrical resistance, the resulting theory is called “ideal MHD” in contrast to “resistive MHD” with finite conductivity. In the ideal case equation (6) yields . ${\ displaystyle \ sigma = \ infty}$ ${\ displaystyle \ mathbf {E} \ cdot c = - \ mathbf {v} \ times \ mathbf {B}}$

Examples of the applicability of the ideal MHD can be found, for example, in the calculation of plasma flows in connection with nuclear fusion or stellar corons . In addition, it is often assumed that the plasma is incompressible (i.e. ) and that there is no internal friction ( viscosity ). ${\ displaystyle \ partial _ {t} \ rho = 0}$

Frozen magnetic field

The MHD combines the hydro- and electrodynamic properties of plasmas. Material movements and the behavior of the magnetic field are therefore not independent of one another. Plasma movements lead to further magnetic and electrical fields, which in turn lead to electrical currents inside the plasma .

An important special case arises for the case of the ideal MHD. Here the electrical resistance of the plasma disappears and the induction equation takes shape

{\ displaystyle \ partial _ {t} \ mathbf {B} = \ nabla \ times (\ mathbf {v} \ times \ mathbf {B})}

on. It can be shown that in this case plasma and magnetic field are coupled; the magnetic field follows the plasma currents. In this case one speaks of a “frozen” magnetic field or, in connection with the ideal induction equation, also of a “flux-maintaining” equation. The morphology of the magnetic field can also be subject to considerable changes in this case, but it is important that no topological changes (therefore no changes in the context of the magnetic field) can occur.

Whether the magnetic field follows the plasma or the plasma follows the magnetic field depends on which component dominates and therefore exerts greater pressure. Both cases can be observed in the sun . While the plasma in the photosphere is very dense and the plasma movements from the convection zone dominate the behavior of the magnetic field, the plasma in the corona is very thin, so that the structure of the corona is dominated by the magnetic field.

Best before waves

Different wave modes can develop inside the plasma . These are the slow and fast magnetoacoustic waves and the so-called Alfvén waves . These modes represent special cases for waves that propagate either parallel or perpendicular to the magnetic field. They give an insight into the basic physical phenomena. In the general case, however, one will have to deal with a superposition of all modes.

Applications

The MHD has a wide range of applications in both engineering and the natural sciences.

Geo- and solar dynamo

The earth's magnetic field is generated by the so-called geodynamo , which is described by the equations of magnetohydrodynamics. The earth's magnetic field arises in the outer core of the earth , which mainly consists of liquid iron (see formation and maintenance of the earth's magnetic field (geodynamo) ).

The partial differential equations occurring in connection with a geodynamo can only be solved analytically in highly simplified cases. Since the mid-1990s, numerical methods have provided the first approaches to understanding the dynamics of the earth's magnetic field .

The situation is similar with the magnetic field of the sun and other stars of a similar spectral type . The creation of their magnetic fields results from the interaction of several factors in the outer layers of the stars ( dynamo theory ) and is also described with models based on the MHD.

Stellar atmospheres

The corona (outermost atmosphere) of the sun and other stars is a highly structured area with very low plasma densities in which the magnetic field is the dominant, structural component. MHD effects are very important here in order to describe and understand the division and dynamics of this outer stellar atmosphere. The MHD also plays an important role in the underlying atmospheric layers of the chromosphere and photosphere .

Electromagnetic flow control

Magnetic fields are used in metallurgy to influence the flow of liquid metals such as steel or aluminum. A distinction must be made between static and time-dependent magnetic fields during application. Static (time-independent) magnetic fields dampen turbulence and are therefore used in the form of magnetic brakes (electromagnetic brakes) in the continuous casting of steel. Time-dependent magnetic fields are used for electromagnetic support when casting aluminum (electromagnetic casting).

Optimization of electrochemical processes

The influence of a magnetic field on electrochemical applications is called magnetoelectrochemistry . Due to the MHD, this causes a convection flow in the electrolyte when current flows. In this way, higher current densities can be achieved in electrolysis, for example in metal deposition.

Electromagnetic flow measurement

If an electrically conductive fluid moves under the influence of a magnetic field, a voltage is generated in the fluid which is proportional to the strength of the magnetic field and the flow velocity. This principle was discovered in 1832 by Michael Faraday, who tried (unsuccessfully) in this way to determine the flow velocity of the Thames. The principle is found today in the form of electromagnetic flow meters (also called inductive flow meters ), widely used in the food industry, the chemical industry and in waterworks. When an electrically conductive fluid moves in a magnetic field, eddy currents also arise in the fluid due to the induced voltage. These generate a Lorentz force in the fluid that counteracts the movement. This physical effect is used in the non-contact flow measurement method known as Lorentz force anemometry .

Best before generator

A technical application of magnetohydrodynamics is the magnetohydrodynamic generator (MHD generator). A plasma is shot through between two conductive electrodes . A magnetic field is applied perpendicular to the electrodes, which then separates the negatively charged electrons and the positively charged ions due to the opposing charge. This creates a voltage difference between the plates . In this way, kinetic energy can be converted directly into electrical energy without having to use mechanical components ( turbines or generators ). Despite intensive efforts, especially in the 1960s, it was not possible to develop electrodes that were stable over the long term. For this reason, the MHD generator is currently of no practical importance.

MHD drive

An electrically conductive substance, such as a plasma, can be accelerated in an electromagnetic field ( magnetoplasmic dynamic drive ). Since sea water and ionized air are also conductive as ion mixtures, they can also be accelerated in an electromagnetic field ( magnetohydrodynamic drive ). In principle, these properties can be used to propel ships, submarines and aircraft. However, the efficiency of such systems is low. For this reason, the MHD drive has no practical significance today.

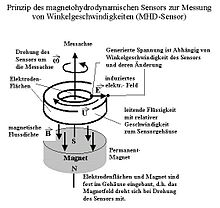
Best before sensor

Magnetohydrodynamic sensors are used to measure angular velocities. Accuracy increases with size. One area of application is the aerospace industry. The principle of an MHD sensor, which also helps to understand the basic idea of magnetohydrodynamics (MHD) as a whole, is shown in this sketch.

Web links

Bibliography

Eugene N. Parker : Cosmical Magnetic Fields: Their Origin and their Activity . Oxford University Press, Oxford 1979. ISBN 978-0-19-851290-5 .
Arnold O. Benz: Plasma Astrophysics - Kinetic Processes in Solar and Stellar Coronae. 1993, ISBN 0-7923-2429-3 .
JP Goedbloed: Principles of magnetohydrodynamics - with applications to laboratory and astrophysical plasmas. Cambridge Univ. Press, Cambridge 2004, ISBN 0-521-62347-2 .
Peter A. Davidson: An introduction to magnetohydrodynamics. Cambridge Univ. Press, Cambridge 2006, ISBN 978-0-521-79487-9 .
CG Campbell: Magnetohydrodynamics in binary stars. Kluwer, Dordrecht 1997, ISBN 0-7923-4606-8 .
Leonard F. Burlaga: Interplanetary magnetohydrodynamics. Oxford Univ. Pr., New York 1995, ISBN 0-19-508472-1 .