Side-Looking Airborne Radar

Angle named in the literature for SLAR:
β = incidence angle ,
ε = depression angle , due to
the curvature of the earth unequal to the grazing angle γ
θ = 90 ° - ε = viewing angle (eng .: look angle or
off-nadir angle )
γ = grazing angle (engl .: grazing angle )
θ = ε + 90 ° = angle for use in spherical coordinates

Further in the literature named angle at SLAR:
α = cone angle (engl .: cone angle )
φ = azimuth angle (engl .: azimuth angle )
, the projection of α represents the earth surface.

Side Looking Airborne Radar ( SLAR , German airborne side view radar ) describes a group of imaging radar methods for remote sensing . From a moving platform (e.g. aircraft or satellite ), a radar sequentially detects the landscape overflown sideways to the direction of movement. SLAR was formerly the generic term for all airborne or space-based radar devices not used as nose radar ( forward looking radar ) or radar altimeter , but since the introduction of Synthetic Aperture Radar (SAR) it has only been used in historical considerations of SAR and describes radar with a real aperture (RAR).

The SLAR was developed for military use around 1951. It was used from 1960 for civil purposes (remote sensing of the earth's surface). The further development to the SAR was first described in 1952/53 and was ready for use in the mid-1950s. A synthetic aperture (SAR) with intrapulse-modulated transmission pulses is usually used. Special applications can also use the measuring methods of a frequency-modulated continuous wave radar , which are much more precise than pulse radar .

Basics

geometry

The SLAR has a more favorable illumination of the scenery than a ground penetrating radar. The radar looks obliquely from above with the viewing or viewing angle θ (engl .: looking angle ) laterally to the area to be measured. The line of sight is often exactly perpendicular to the direction of flight, but a squinted mode - a " cross-eyed look" deviating from a right angle is also possible. In this case, the angle α is measured, which is called the cone angle because of its importance for the Doppler frequency of the echo signal. Here, a look angle is in the literature sometimes θ _sq (ger .: squint angle ) called that deals with θ _sq = 90 ° - α results. The projection of the cone angle to the earth's surface is the side angle φ (ger .: azimuth angle ).

As is customary with any radar, the measurements are initially carried out in spherical coordinates : as a side angle or azimuth (as a function of the directional effect of the antenna) and an inclined distance (as a function of the transit time measurement of the echo signal) at a specified elevation angle ϑ . Both measured variables are related to the current location of the carrier platform and must be converted into a Cartesian coordinate system . This coordinate system has its origin in the radar antenna (more precisely: in its phase center ) and its X-axis lies on the flight path of the carrier platform. The Z-axis is perpendicular to this as the direction for measuring the flight altitude . The unit vector points from the antenna to the reflecting object ( called the ground scatterer here ). ${\ displaystyle {\ vec {u}} = (u, v, w) ^ {t}}$

When converting the sequence of the measured echo signals into an image of the illuminated area, distortions occur depending on the viewing angle, which must be compensated for by complex procedures.

Dynamics of the received signals

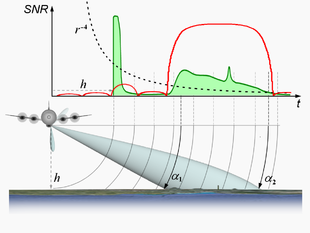
The strength of the echo signal (green) depends on the antenna diagram (red) and the two-way attenuation (dashed)

The strength of the echo signal depends on the two-way attenuation ( r ⁻⁴ dependence - see radar equation ) and the antenna diagram. Both influences cause a roughly sawtooth-shaped amplitude modulation of the echoes in the main lobe. Reflecting objects or surfaces lying in the close range deliver significantly stronger echo signals than objects in the far range. An enlargement of the illuminated area with increasing distance (e.g. based on the model of a so-called volume target in weather radar ) is counteracted by poorer reflection ( retroreflection ) due to the reduced grazing angle γ and a reduction in the power density at the point of reflection by a factor of 1 / cos γ .

The first echo signal on the time axis is always the so-called "nadir return". Although the base point (nadir) is not covered by the antenna diagram, this nadir forms a very strong echo signal due to the lower two-way attenuation and the increased proportion of specular reflection, which is usually received by side lobes . The time delay to the transmission pulse is the measure for the current altitude of the aircraft.

Spatial resolution

The lateral view allows the good range resolution determined by the transmitter bandwidth B of the radar pulses to be converted into a horizontal resolution on the ground. The resolving power in the radial direction (transverse to the direction of flight) depends on the grazing angle γ : the steeper the radar looks downwards, the worse the resolution in this direction on the ground. (Only in the case of SLAR in aircraft with low to medium flight altitudes and with a level illumination zone, the grazing angle can be equated to the depression angle ε , neglecting the earth's curvature .) The distance resolution δ _{g in} relation to the earth's surface is calculated according to:

{\ displaystyle \ delta _ {g} = {\ frac {c_ {0}} {2B \ cdot \ cos \ gamma}} \,}

with c ₀ as the speed of light in free space.

A larger viewing angle improves this value at the expense of poorer resolution in the direction of flight, weaker echo signals due to the greater slanting distance and possible shadows in steep terrain. Since the reflections of the individual points on the ground arrive at the radar antenna at different times depending on the inclined distance, the antenna diagram does not have to be swiveled in order to achieve a distance resolution. The chronological order, however, contains strong distortions due to the height differences on the ground.

Transverse to the viewing direction (in azimuth , or germ .: cross range ), the resolving power depends largely on the directivity of the antenna as well as the slant range r ( slant range ab). With the SLAR, it is a little better than the width of the illumination zone (see the third graphic). The directivity is broken down by the half- width (−3 dB opening angle) of the antenna, which is approximately equal to the ratio of the diameter of the real aperture D of the radar antenna to the wavelength λ used :

{\ displaystyle \ delta _ {cr} = {\ frac {r \ lambda} {D}}}

In other words, in the case of a SLAR, the cross range resolution δ _cr depends on the slant distance r . The higher the flight altitude and the flatter the radar looks, the worse the resolution of a SLAR with a real aperture (RAR) becomes. Due to this limitation, the RAR is only suitable to a limited extent for satellites.

Foreshortening : The front flank of a mountain appears shortened in the image.

Distortions

A fundamental non-linear distortion arises in the distance display by measuring an inclined distance and the necessary projection of this into a corresponding scale representation of the distance on the ground. In older viewing devices, which displayed the image in real time, this was approximately achieved by a non-linear deflection speed of the cathode ray of the picture tube . However, this technology only works under the assumption that there is a flat surface without significant differences in height.

Due to the viewing angle (or, as a complement to this, the depression angle, which is usually between 10 and 50 °), the measurements of the inclined distance contain an error due to different terrain heights. Terrain surfaces inclined towards the SLAR are shown abbreviated in the image of the terrain surface. Terrain points higher up are shown offset from the origin of the coordinate system. As a result, the slopes that are oriented towards the SLAR are shortened ( foreshortening ). If the slope is greater than the angle of depression, the reduction goes into a superposition (Engl. Layover ) about: The summit is shown in the image before the bottom of the hill. Behind the slopes facing away from the radar, shadows can appear in which no information is available from the radar and in the area of which only noise is received. A very simple trigonometric method of calculating a relative height is to multiply the length of the shadow by the tangent of the depression angle.

Due to the poor resolution of the RAR, these distortions are practically only of greater significance with SAR and are corrected there with a special Fast Delivery (FD) algorithm when the image is created. Serious deviations can be corrected after repeated skimming and comparing the data from different angles of depression. By flying in parallel, stereo image pairs can also be generated, which enable the distortions to be corrected mathematically by viewing the same object at different angles of depression.

Terms related to SLAR procedures

Scheme of the image acquisition of a SLAR with real aperture

The figure on the right shows a SLAR moving with an airplane at altitude h above ground.

Illuminating zone (English footprint ): Field of view of the antenna on the ground (in the figure the blue area of the ellipse).

Further developments

High PRF mode

High PRF mode: τ = transmission pulse duration, T = pulse period

In order to improve the energy balance of the radar (and thus its range) and at the same time the data renewal rate, the high PRF mode is mostly used. A very high pulse repetition frequency is used here at the expense of the unambiguousness of the measuring distance. The pulse periods are much shorter than the necessary duration of the pulses. Several transmission pulses travel simultaneously between the radar and the surface of the earth to be displayed. The measurement results of the transit time are "folded", so the echoes from several previous pulse periods are received in one pulse period.

This mode is possible because there are hardly any obstacles on the way from the radar to the earth's surface. In addition, up to three different pulse modulations with often seven different pulse period lengths are used with the pulse compression method (as a distinguishing feature for the individual pulses) . In this way, the software can “unfold” the echo signals, i.e. assign them to their original transmission pulse, and enable a clear determination of the distance. As a side effect, ambiguities in the Doppler frequency can no longer occur, since such ambiguities are tied to a small pulse repetition frequency. The disadvantage is that losses of 1 to 2 dB now occur, a so-called eclipsing loss , because the receiver is switched off at the moment of transmission with many types of duplexers and the echo signals arriving during this time cannot be processed.

Doppler Beam Sharpening (DBS)

Improvements in azimuth or cross range resolution can be achieved by evaluating the Doppler frequency , known as Doppler Beam Sharpening. Since the radar is the reference point in the system, fixed reflectors have a radial velocity to the radar platform. The size of the Doppler shift of your echoes depends on the angle between the line of sight and the direction of flight. There is no Doppler effect across the flight direction because the radial velocity is zero. Narrow-band filtering allows you to differentiate between several angles within the antenna lobe , which increases the resolution in the direction of flight accordingly. The effective aperture of the antenna is the flight distance covered during this period. Space probes in highly elliptical orbits are particularly suitable for this procedure due to their high flight speed in the periapsis . In 1983/4, for example, the Venera 15 and 16 probes mapped parts of the Venus surface with a resolution of only one kilometer. This method is only effective from a lateral angle that deviates more than 15 ° from the direction of flight. The DBS process is still used in Bugradargeräten that a sector-PPI-screen use and improves the angular resolution of the radar there from (for example at a. X-band - parabolic antenna ) of 4 ° to 0.5 °.

In retrospect, the DBS filter method was recognized as an SAR method and is now sometimes referred to as incoherent SAR (although modern nose radars that use this method now also work fully coherently), the classic SLAR as RAR ( radar with real aperture ).

Synthetic Aperture Radar (SAR)

The same transit time defines a sphere around the radar, the same Doppler frequency forms a cone in the direction of flight. The sections of these figures form isorange and isodoppler lines on the surface of the earth

The SAR uses a relatively small antenna as a single radiator and stores the complete pulse periods of the echo signals. Later, a sharp image is calculated from these individual periods, which has a much higher resolution than the Real Aperture Radar with a relatively large antenna. It will

unfocused SAR: - non-focused SAR - (as caused by the previously limited computing power) and
focused SAR: - focused SAR -

are differentiated, whereby the focused SAR can undertake a distance-dependent phase correction of the echo signals that is necessary due to differences in transit time. In the classic SAR method, the azimuthal ( cross range ) resolution is only dependent on the synthetic aperture length and therefore independent of the slant distance r and the wavelength λ . Nowadays, the term SAR is only understood to mean focused SAR . The intersection points of the lines of the same distance measurement ( isoranges ) and the same Doppler frequency ( Iso-Doppler or Isodops ) are used to determine the direction very precisely .

The improvements in resolving power would be achieved using the same radar antenna, transmitter and receiver, only by different software in the radar data processor (RDP). In the literature, the theoretically achievable resolving power is given for these different radar methods as summarized in the table:

Framework conditions for the table:

r = 100 km, slant range for an assumed extremely low altitude of a satellite.
γ = 30 °, grazing angle (cos γ ≈ 0.866)
λ ≈ 3 cm, wavelength for a radar in the X band
D = 2 m, diameter of the antenna with real aperture

Airspeed 180 m / s, length of the synthetic aperture under these conditions in stripmap mode about 750 m, in spot-light mode about 5000 m.

Procedure	Azimuthal resolving power
SLAR (RAR)	1500 m
Doppler Beam Sharpening (DBS)	150 m
SAR (not focused)	27 m
SAR (focused)	1 m
Spotlight SAR	0.3 m

↑ ^a ^b Synthetic Aperture Radar in the stripmap method (for stripmap and spotlight mode see: Special SAR methods )

The possible improvements through SAR do not affect the resolving power in the distance (in the radial direction). Here the resolution is limited by the bandwidth of the transmitted signal. The pulse compression method is used to achieve a good energy balance with a good range resolution at the same time in a radar device . For a transmitter bandwidth of 100 MHz (corresponds to about 1% of the transmission frequency), a distance resolution of 1.5 m is theoretically possible. Due to the oblique viewing direction with the above angles, this results in a resolution of about 1.7 m on the ground. Often, the parameters of the SAR are chosen to achieve a comparable resolution in the azimuth range in order to fill an approximately square pixel in the image , which is called the range bin . The size of this range bins is usually set at about half the resolution in order to obtain a sharp representation even if an object of the order of magnitude of the resolution falls exactly between two range bins . In the radar signal processing, the storage capacities are then aligned to this range bin size.

Due to its dependence on the transmission frequency, evaluations of the Doppler frequency are only possible if the Doppler frequency is "normalized" when using a linear frequency-modulated transmission pulse, i.e. this frequency dependency is removed by division with the current transmission frequency. This process is also called de-ramping .

literature

George W. Stimson, "Introduction to Airborne Radar," 2nd Ed., 2000 Raleigh: SciTech Publishing, ISBN 9781891121159 .
R. Sullivan, "Synthetic aperture radar", in M. Skolnik, Radar Handbook, 3rd Ed., 2008 New York: McGraw-Hill, ISBN 978-0-07-148547-0 .

Web links

Wiktionary: Side view radar - explanations of meanings, word origins, synonyms, translations

Radar Remote Sensing (English)
Radar Course (English)
Radar tutorial (German, English, French, Turkish)

Individual evidence

↑ DIN 18716-3 - German Institute for Standardization : Photogrammetry and Remote Sensing, Part 3: Terms of Remote Sensing . Beuth, Berlin, 1997.
^ Moore, Richard K. "Imaging Radar Systems", in Manual of Remote Sensing 2nd ed. Vol. I eds. 1983 David S. Simonett, Fawwaz T. Ulaby, American Society of Photogrammetry.
↑ Carver, Keith, R., Charles Elachi, Fawwaz T. Ulaby, 1985: “Microwave Remote Sensing from Space,” in Proceedings of the IEEE , Vol. 73, no. 6, pp. 970-996
↑ CW Sherwin, JP Ruina, and RD Rawliffe, “Some early developments in synthetic aperture radar systems,” IRE Transactions on Military Electronics, vol. MIL-6, no. 2, pp. 111-115, April 1962 ( ISSN 0096-2511 )
^ ^A ^b ^c R. Sullivan, "Synthetic aperture radar", in M. Skolnik, Radar Handbook, 3rd Ed., 2008 New York: McGraw-Hill, ISBN 978-0-07-148547-0 .

[SAR-6] Synthetic Aperture Radar in the stripmap method (for stripmap and spotlight mode see: Special SAR methods )

[1] DIN 18716-3 - German Institute for Standardization : Photogrammetry and Remote Sensing, Part 3: Terms of Remote Sensing . Beuth, Berlin, 1997.

[2] Moore, Richard K. "Imaging Radar Systems", in Manual of Remote Sensing 2nd ed. Vol. I eds. 1983 David S. Simonett, Fawwaz T. Ulaby, American Society of Photogrammetry.

[3] Carver, Keith, R., Charles Elachi, Fawwaz T. Ulaby, 1985: “Microwave Remote Sensing from Space,” in Proceedings of the IEEE , Vol. 73, no. 6, pp. 970-996

[4] CW Sherwin, JP Ruina, and RD Rawliffe, “Some early developments in synthetic aperture radar systems,” IRE Transactions on Military Electronics, vol. MIL-6, no. 2, pp. 111-115, April 1962 ( ISSN 0096-2511 )

[Sullivan-5] A ^b ^c R. Sullivan, "Synthetic aperture radar", in M. Skolnik, Radar Handbook, 3rd Ed., 2008 New York: McGraw-Hill, ISBN 978-0-07-148547-0 .