One-step process
In numerical mathematics, one-step methods are, in addition to the multi-step methods, a large group of calculation methods for solving initial value problems . This task, in which a common differential equation is given together with a starting condition, plays a central role in all natural and engineering sciences and is also gaining more and more importance, for example, in economics and social sciences. Initial value problems are used to analyze, simulate, or predict dynamic processes.
The name-giving basic idea of the one-step method is that, starting from the given starting point, it calculates approximation points step by step along the sought solution. In doing so, they only use the most recently determined approximation for the next step, in contrast to the multi-step method, which also include points that were further back in the calculation. The one-step methods can be roughly divided into two groups: the explicit methods, which calculate the new approximation directly from the old one, and the implicit methods, in which an equation has to be solved. The latter are also suitable for so-called stiff initial value problems.
The simplest and oldest one-step method, the explicit Euler method , was published by Leonhard Euler in 1768 . After a group of multi-step processes had been presented in 1883, Carl Runge , Karl Heun and Wilhelm Kutta developed significant improvements to Euler's process around 1900 . From these emerged the large group of the Runge-Kutta processes , which form the most important class of one-step processes. Further developments of the 20th century are, for example, the idea of extrapolation , but above all considerations for step size control, i.e. for the selection of suitable lengths for the individual steps of a method. These concepts form the basis to be able to solve difficult initial value problems, as they occur in modern applications, efficiently and with the required accuracy using computer programs.
introduction
Ordinary differential equations
The development of differential and integral calculus by the English physicist and mathematician Isaac Newton and independently of it by the German polymath Gottfried Wilhelm Leibniz in the last third of the 17th century was an essential impetus for the mathematization of science in the early modern period . These methods formed the starting point of the mathematical branch of analysis and are of central importance in all natural and engineering sciences. While Leibniz was led by the geometric problem of determining tangents to given curves to differential calculus, Newton started from the question of how changes in a physical quantity can be determined at a certain point in time.
For example, when a body moves, its average speed is simply the distance traveled divided by the time it took. However, in order to mathematically formulate the current speed of the body at a certain point in time , a limit crossing is necessary: one considers short periods of length , the distances covered and the associated average speeds . If you let the time span converge to zero and if the average speeds also approach a fixed value , then this value is called the (instantaneous) speed at the given point in time . Designates the position of the body at the time , then one writes and names the derivative of .
The decisive step in the direction of differential equation models is now the opposite question: In the example of the moving body, the speed is known at all times and its position is to be determined from this. It is clearly clear that the initial position of the body must also be known at a point in time in order to be able to solve this problem clearly. It is a function of searching that the initial condition with given values and fulfilled.
In the example of determining the position of a body from its speed, the derivation of the function sought is explicitly given. Usually, however, there is the important general case of ordinary differential equations for a desired quantity : Based on the laws of nature or the model assumptions, a functional relationship is known that indicates how the derivation of the function to be determined can be calculated from and from the (unknown) value . In addition, an initial condition must be given again , which can be obtained, for example, from a measurement of the required variable at a fixed time. In summary, we have the following general type of problem: Find the function that contains the equations
where is a given function.

A simple example is a size that grows exponentially . This means that the current change, i.e. the derivative, is proportional to itself. So it applies with a growth rate and, for example, an initial condition . In this case, the solution you are looking for can already be found using elementary differential calculus and specified using the exponential function : It applies .
The function sought in a differential equation can be vector-valued , that is, for each there can be a vector with components. One then speaks of a -dimensional differential equation system. In the case of a moving body, its position in -dimensional Euclidean space and its speed are at the time . The differential equation therefore specifies the speed of the trajectory sought with direction and magnitude at each point in time and space . The path itself should be calculated from this.
Basic idea of the one-step process
In the simple differential equation of exponential growth considered as an example above, the solution function could be specified directly. This is generally no longer possible with more complex problems. Under certain additional conditions, one can then show for the function that a uniquely determined solution of the initial value problem exists; However, this can then no longer be calculated explicitly using analysis methods (such as separation of variables , an exponential approach or variation of the constants ). In this case, numerical methods can be used to determine approximations for the solution sought.
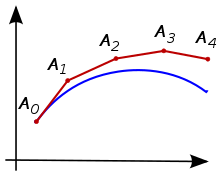
The methods for the numerical solution of initial value problems of ordinary differential equations can be roughly divided into two large groups: the one-step and the multi-step method. Both groups have in common that they gradually calculate approximations for the desired function values at points . The defining property of the one-step method is that only the “current” approximation is used to determine the following approximation . In contrast, in the case of multi-step procedures, previously calculated approximations are also included; a three-step method would therefore, for example, also use and to determine the new approximation .
The simplest and most fundamental one-step method is the explicit Euler method , which the Swiss mathematician and physicist Leonhard Euler presented in his textbook Institutiones Calculi Integralis in 1768 . The idea of this method is to approximate the solution sought by a piece-wise linear function in which the slope of the straight line is given in every step from point to point . More precisely: The problem already gives a value for the function sought, namely . But the derivation at this point is also known, because it applies . The tangent to the graph of the solution function can thus be determined and used as an approximation. At this point there is a step size
- .
This procedure can now be continued in the following steps. Overall, this results in the calculation rule for the explicit Euler method
with the step sizes .
The explicit Euler method is the starting point for numerous generalizations in which the slope is replaced by slopes that approximate the behavior of the solution between the points and more precisely. The implicit Euler method, which is used as the slope, provides an additional idea for one-step methods . At first glance, this choice seems unsuitable, as it is unknown. However, the equation is now obtained as a process step
from which (if necessary by a numerical method) can be calculated. If, for example, the arithmetic mean of the slopes of the explicit and the implicit Euler method is selected as the slope, then the implicit trapezoid method is obtained . An explicit method can be obtained from this, for example, if the unknown on the right-hand side of the equation is approximated by the explicit Euler method, the so-called Heun method . All these procedures and all further generalizations have the basic idea of the one-step procedure in common: the step
with a slope that can depend on , and and (in the case of implicit methods) on.
definition
With the considerations from the introductory section of this article, the concept of the one-step procedure can be defined as follows: We are looking for the solution to the initial value problem
- , .
It is assumed that the solution
exists on a given interval and is uniquely determined. are
Intermediate points in the interval and the associated step sizes, then that means through
- ,
given procedures one-step procedure with procedure function . If it doesn't depend on, then it's called an explicit one-step procedure . Otherwise an equation for has to be solved in each step and the procedure is called implicit .
Consistency and Convergence
Convergence order
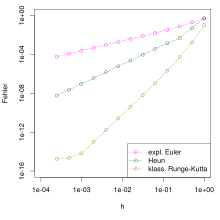
For a practicable one-step method, the calculated good approximations for the values of the exact solution should be at the point . Since the quantities are generally -dimensional vectors, the quality of this approximation is measured with a vector norm as , the error at the point . It is desirable that these errors quickly converge to zero for all if the step sizes are allowed to converge to zero. In order to also cover the case of non-constant step sizes, one defines more precisely as the maximum of the used step sizes and considers the behavior of the maximum error at all points in comparison to powers of . It is said that the one-step procedure for solving the given initial value problem has the order of convergence if the estimate
holds for all sufficiently small with a constant that is independent of .
The order of convergence is the most important parameter for comparing different one-step methods. A method with a higher order of convergence generally delivers a smaller total error for a given step size or, conversely, fewer steps are required to achieve a given accuracy. In the case of a method with, it is to be expected that if the step size is halved, the error is only roughly halved. In the case of a method of the order of convergence , however, one can assume that the error is reduced by approximately the factor .
Global and local error
The errors considered in the definition of the order of convergence are made up of two individual components in a manner that initially appears complicated: Of course, they depend on the one hand on the error that the procedure makes in a single step, in that the unknown slope of the function sought is replaced by the Procedural function approximates. On the other hand, it must also be taken into account that the starting point of a step generally does not already coincide with the exact starting point ; the error after this step also depends on all errors that have already been made in the previous steps. Due to the uniform definition of the one-step procedure, which only differs in the choice of the procedural function , it can be proven that (under certain technical conditions ) one can infer the convergence order directly from the error order in a single step, the so-called consistency order.
The concept of consistency is a general and central concept in modern numerical mathematics. While one examines how well the numerical approximations fit the exact solution during the convergence of a procedure, when it comes to consistency, put simply, one asks the "opposite" question: How well does the exact solution fulfill the procedural specification? In this general theory it holds that a method is convergent if and only if it is consistent and stable . In order to simplify the notation, it should be assumed in the following consideration that an explicit one-step procedure
with a constant step size . The true solution defines the local clipping error (also called local procedural error) as
- .
So one assumes that the exact solution is known, starts a process step at that point and forms the difference to the exact solution at the point . This defines: A one-step procedure has the order of consistency if the estimate
holds for all sufficiently small with a constant that is independent of .
The noticeable difference between the definitions of the order of consistency and order of convergence is the power instead of . This can be clearly interpreted in such a way that a power of the step size is “lost” during the transition from the local to the global error. The following principle applies, which is central to the theory of the one-step procedure:
- If the process function is Lipschitz continuous and the associated one-step process has the order of consistency , then it also has the order of convergence .
The Lipschitz continuity of the process function as an additional requirement for stability is generally always fulfilled when the function from the differential equation is itself Lipschitz continuous. This requirement has to be assumed for most applications anyway, in order to guarantee the unambiguous solvability of the initial value problem. According to the sentence, it is sufficient to determine the consistency order of a one-step procedure. In principle, this can be achieved by a Taylor expansion of to powers of . In practice, the resulting formulas for higher orders become very complicated and confusing, so that additional concepts and notations are required.
Stiffness and A-stability
The convergence order of a method is an asymptotic statement that describes the behavior of the approximations when the step size converges to zero. However, it does not say anything about whether the method actually calculates a usable approximation for a given fixed step size. Charles Francis Curtiss and Joseph O. Hirschfelder first described in 1952 that this can actually be a big problem with certain types of initial value problems . They had observed that the solutions of some systems of differential equations of chemical reaction kinetics could not be calculated using explicit numerical methods, and they named them such initial value problems "stiff". There are numerous mathematical criteria for determining how stiff a given problem is. Clearly, rigid initial value problems are mostly systems of differential equations in which some components become constant very quickly, while other components change only slowly. Such behavior typically occurs when modeling chemical reactions. The most useful definition of stiffness for practical application is: An initial value problem is stiff if one would have to choose the step size “too small” in order to obtain a usable solution when solving it with explicit one-step methods. Such problems can only be solved with implicit procedures.
This effect can be illustrated more precisely by examining how the individual methods cope with exponential decay . To do this, consider the test equation according to the Swedish mathematician Germund Dahlquist
with the exponentially decreasing solution . The graphic on the right shows - as an example of the explicit and the implicit Euler method - the typical behavior of these two groups of methods in this seemingly simple initial value problem: If one uses too large a step size in an explicit method, then strongly oscillating values result, which are in the Build up the calculation and move further and further away from the exact solution. Implicit methods, on the other hand, typically calculate the solution qualitatively correctly for any step sizes, namely as an exponentially decreasing sequence of approximate values.
The above test equation is also considered somewhat more generally for complex values of . In this case, the solutions oscillations whose amplitude remains bounded if if applicable, ie the real component of less than or equal to 0. This allows a desirable property of one-step methods to be formulated, which are to be used for stiff initial value problems: the so-called A-stability. A method is called A-stable if it is applied to the test equation for any step size and calculated for all with a sequence of approximations which (like the true solution) remains constrained. The implicit Euler method and the implicit trapezoid method are the simplest examples of A-stable one-step methods. On the other hand, it can be shown that an explicit procedure can never be A-stable.
Special processes and process classes
Simple procedures of order 1 and 2
As the French mathematician Augustin-Louis Cauchy proved around 1820, the Euler method has the order of convergence 1. If the slopes of the explicit Euler method and the implicit Euler method , as they exist at the two end points of a step, can be averaged hope to get a better approximation over the whole interval. In fact, it can be proven that the implicit trapezoidal method thus obtained
the convergence order has 2. This method has very good stability properties, but is implicit, so that an equation for has to be solved in each step . If this quantity is approximated on the right-hand side of the equation using the explicit Euler method, Heun's explicit method is created
- ,
which also has the convergence order 2. Another simple explicit method of order 2, the improved Euler method , can be obtained by considering the following: A “mean” slope in the process step would be the slope of the solution in the middle of the step, i.e. at the point . However, since the solution is unknown, it is approximated by an explicit Euler step with half the step size. The procedural rule results
- .
These one-step methods of order 2 were all published in 1895 by the German mathematician Carl Runge as improvements to the Euler method .
Runge-Kutta method
The mentioned ideas for simple one-step methods lead, if they are further generalized, to the important class of Runge-Kutta methods. For example, Heun's method can be presented more clearly as follows: First an auxiliary slope is calculated, namely the slope of the explicit Euler method. This determines another auxiliary slope, here . The method gradient actually used then results as a weighted mean of the auxiliary slopes, in the Heun method . This procedure can be generalized to more than two auxiliary slopes. A -step Runge-Kutta method first calculates auxiliary slopes by evaluating them at suitable points and then as a weighted mean. In the case of an explicit Runge-Kutta method, the auxiliary slopes are calculated directly one after the other; in the case of an implicit method, they result as solutions to a system of equations. A typical example is the explicit classic Runge-Kutta method of order 4, which is sometimes simply referred to as the Runge-Kutta method: First, the four auxiliary slopes are used
and then the weighted average as the process slope
used. The German mathematician Wilhelm Kutta published this well-known method in 1901, after Karl Heun had found a three-step, one-step method of order 3 a year earlier .
The construction of explicit processes of even higher order with the smallest possible number of stages is a mathematically very demanding problem. As John C. Butcher was able to show in 1965, there are, for example, only a minimum of six-step procedures for order 5; an explicit Runge-Kutta method of the 8th order requires at least 11 steps. In 1978 the Austrian mathematician Ernst Hairer found a procedure of order 10 with 17 steps. The coefficients for such a procedure must satisfy 1205 determining equations. With implicit Runge-Kutta methods, the situation is simpler and clearer: for every number of stages there is a method of order ; this is at the same time the maximum attainable order.
Extrapolation method
The idea of extrapolation is not limited to solving initial value problems with one-step methods, but can be applied analogously to all numerical methods that discretize the problem to be solved with a step size . A well-known example of an extrapolation method is the Romberg integration for the numerical calculation of integrals. In general, let therefore be a value that is to be determined numerically, in the case of this article the value of the solution function of an initial value problem at a given point. A numerical method, for example a one-step method, calculates an approximate value for this , which depends on the choice of the step size . Here, it is assumed that the method is convergent, ie that against if converges converges to zero. This convergence, however, is only a purely theoretical statement, since in real application of the method approximate values can be calculated for a finite number of different step sizes, but of course you cannot let the step size "converge towards zero". The calculated approximations for different step sizes can, however, be understood as information about the (unknown) function : In the extrapolation method , an interpolation polynomial is used as an approximation, i.e. a polynomial with
for . The value of the polynomial at the point is then used as a calculable approximation for the non-calculable limit value of for towards zero. Roland Bulirsch and Josef Stoer published an early successful extrapolation algorithm for initial value problems in 1966.
A concrete example in the case of a one-step method of order can make the general procedure of extrapolation understandable. With such a method, the calculated approximation for small step sizes can be easily converted into a polynomial of the form
with initially unknown parameters and approximate. Now is calculated by the method for a pitch and half pitch of two approximations and are obtained from the interpolation conditions , and two linear equations for the unknowns and . The value extrapolated to
then generally represents a much better approximation than the two values initially calculated. It can be shown that the order of the one-step process obtained in this way is at least , i.e. at least 1 greater than in the original process.
Procedure with step size control
One advantage of the one-step method is that any step size can be used in each step independently of the other steps . In practice, the question obviously arises as to how to choose . In real applications there will always be an error tolerance with which the solution of an initial value problem is to be calculated; For example, it would be pointless to determine a numerical approximation that is significantly “more precise” than the data with measurement errors for starting values and parameters of the given problem. The goal will therefore be to choose the step sizes so that, on the one hand, the specified error tolerances are adhered to, but on the other hand, to use as few steps as possible in order to keep the computing effort small. In general, this can only be achieved if the step sizes are adapted to the course of the solution: small steps where the solution changes significantly, large steps where it is almost constant.
In the case of well-conditioned initial value problems, it can be shown that the global procedural error is approximately equal to the sum of the local truncation errors in the individual steps. Therefore, as large a step size as possible should be selected for which is below a selected tolerance threshold. The problem here is that it cannot be calculated directly, since it depends on the unknown exact solution of the initial value problem at the point . The basic idea of step size control is therefore to approximate with a method that is more precise than the basic method on which it is based.
Two basic ideas for step size control are the step size halving and the embedded procedures . When halving the step size, the result for two steps with half the step size is calculated as a comparison value in addition to the actual process step. A more precise approximation for is then determined from both values by extrapolation , and the local error is thus estimated. If this is too large, this step is discarded and repeated with a smaller step size. If it is significantly smaller than the specified tolerance, the step size can be increased in the next step. The additional computational effort for this step size halving method is relatively large; therefore, modern implementations mostly use so-called embedded methods for step size control. The basic idea is to calculate two approximations for each step using two one-step methods that have different orders of convergence, and thus to estimate the local error. In order to optimize the computing effort, the two procedures should have as many computing steps as possible in common: They should be “embedded in one another”. For example, embedded Runge-Kutta methods use the same auxiliary slopes and only differ in how they average them. Well-known embedded methods include the Runge-Kutta-Fehlberg methods ( Erwin Fehlberg , 1969) and the Dormand-Prince methods (JR Dormand and PJ Prince, 1980).
Practical example: Solving initial value problems with numerical software
Numerous software implementations have been developed for the mathematical concepts presented in an overview in this article, which enable the user to numerically solve practical problems in a simple manner. As a concrete example, a solution of the Lotka-Volterra equations is to be calculated with the widely used numerical software Matlab . The Lotka-Volterra equations are a simple model from biology that describes the interactions between predator and prey populations . For this purpose the differential equation system is given
with the parameters and the initial condition , . Here and correspond to the temporal development of the prey or predator population. The solution should be calculated on the time interval .
For the calculation using Matlab, the function on the right-hand side of the differential equation is first defined for the given parameter values :
a = 1; b = 2; c = 1; d = 1;
f = @(t,y) [a*y(1) - b*y(1)*y(2); c*y(1)*y(2) - d*y(2)];
In addition, the time interval and the initial values are required:
t_int = [0, 20];
y0 = [3; 1];
Then the solution can be calculated:
[t, y] = ode45(f, t_int, y0);
The Matlab function ode45implements a one-step method that uses two embedded explicit Runge-Kutta methods with orders of convergence 4 and 5 for step size control.
The solution can now be drawn, as a blue curve and as a red one; the calculated points are marked by small circles:
figure(1)
plot(t, y(:,1), 'b-o', t, y(:,2), 'r-o')
The result is shown below in the picture on the left. The right picture shows the step sizes used by the process and was created with
figure(2)
plot(t(1:end-1), diff(t))
This example can also be executed with the free numerical software GNU Octave without changes . With the method implemented there, however, a slightly different step size sequence results.
literature
- John C. Butcher : Numerical Methods for Ordinary Differential Equations . John Wiley & Sons, Chichester 2008, ISBN 978-0-470-72335-7 .
- Wolfgang Dahmen , Arnold Reusken: Numerics for engineers and natural scientists . 2nd Edition. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , chap. 11: Ordinary differential equations .
- Peter Deuflhard , Folkmar Bornemann : Numerical Mathematics 2 - Ordinary Differential Equations . 3. Edition. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 .
- David F. Griffiths, Desmond J. Higham: Numerical Methods for Ordinary Differential Equations - Initial Value Problems . Springer, London 2010, ISBN 978-0-85729-147-9 .
- Robert Plato: Numerical Mathematics compact . 4th edition. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , chap. 7: One-step procedure for initial value problems .
- Hans-Jürgen Reinhardt: Numerics of ordinary differential equations . 2nd Edition. Walter de Gruyter, Berlin / Boston 2012, ISBN 978-3-11-028045-6 .
- Hans Rudolf Schwarz, Norbert Köckler: Numerical Mathematics . 8th edition. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1551-4 , chap. 8: Initial value problems .
- Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerics of ordinary differential equations . 2nd Edition. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 .
Web links
- Lars Grüne: Numerical Methods for Ordinary Differential Equations (Numerical Mathematics II). (PDF) 2008, accessed on August 20, 2018 (lecture notes from the University of Bayreuth ).
- Peter Spellucci: Numerics of ordinary differential equations. (PDF) 2007, accessed on August 20, 2018 (lecture notes from TU Darmstadt ).
- Hans U. Fuchs: Numerical Methods for Differential Equations. (PDF) 2007, accessed on August 20, 2018 (English, lecture notes from the Zurich University of Applied Sciences ).
- Math tutorial: first order general differential equation calculator. In: Math Tutorial. Retrieved August 20, 2018 .
Individual evidence
- ^ Thomas Sonar : 3000 Years of Analysis . Springer, Berlin / Heidelberg 2011, ISBN 978-3-642-17203-8 , pp. 378-388 and 401-426 .
- ↑ Jean-Luc Chabert et al. a .: A History of Algorithms . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , p. 374-378 .
- ↑ Wolfgang Dahmen, Arnold Reusken: Numerics for engineers and natural scientists . 2nd Edition. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , p. 386 f .
- ↑ Wolfgang Dahmen, Arnold Reusken: Numerics for engineers and natural scientists . 2nd Edition. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , p. 386-392 .
- ^ Hans Rudolf Schwarz, Norbert Köckler: Numerical Mathematics . 8th edition. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1551-4 , pp. 350 f .
- ^ Robert Plato: Numerical Mathematics compact . 4th edition. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , pp. 157 .
- ^ Robert Plato: Numerical Mathematics compact . 4th edition. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , pp. 156 .
- ^ Robert Plato: Numerical Mathematics compact . 4th edition. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , pp. 157 .
- ↑ Hans-Jürgen Reinhardt: Numerics of ordinary differential equations . 2nd Edition. Walter de Gruyter, Berlin / Boston 2012, ISBN 978-3-11-028045-6 , p. 42 f .
- ^ John C. Butcher: Numerical Methods for Ordinary Differential Equations . John Wiley & Sons, Chichester 2008, ISBN 978-0-470-72335-7 , pp. 95-100 .
- ^ JC Butcher: Numerical methods for ordinary differential equations in the 20th century . In: Journal of Computational and Applied Mathematics . tape 125 , no. 1–2 , December 15, 2000, pp. 21st f . ( online ).
- ^ Peter Deuflhard, Folkmar Bornemann: Numerical Mathematics 2 - Ordinary Differential Equations . 3. Edition. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , p. 228 f .
- ^ Peter Deuflhard, Folkmar Bornemann: Numerical Mathematics 2 - Ordinary Differential Equations . 3. Edition. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , p. 229-231 .
- ↑ Wolfgang Dahmen, Arnold Reusken: Numerics for engineers and natural scientists . 2nd Edition. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , p. 443 f .
- ↑ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerics of ordinary differential equations . 2nd Edition. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , p. 258 f .
- ↑ Jean-Luc Chabert et al. a .: A History of Algorithms . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , p. 378 f .
- ↑ Jean-Luc Chabert et al. a .: A History of Algorithms . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , p. 381-388 .
- ↑ Wolfgang Dahmen, Arnold Reusken: Numerics for engineers and natural scientists . 2nd Edition. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , p. 406 f .
- ^ JC Butcher: Numerical methods for ordinary differential equations in the 20th century . In: Journal of Computational and Applied Mathematics . tape 125 , no. 1–2 , December 15, 2000, pp. 4-6 ( online ).
- ^ Peter Deuflhard, Folkmar Bornemann: Numerical Mathematics 2 - Ordinary Differential Equations . 3. Edition. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , p. 160-162 .
- ↑ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerics of ordinary differential equations . 2nd Edition. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , p. 219-221 .
- ↑ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerics of ordinary differential equations . 2nd Edition. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , p. 79 ff .
- ^ JC Butcher: Numerical methods for ordinary differential equations in the 20th century . In: Journal of Computational and Applied Mathematics . tape 125 , no. 1–2 , December 15, 2000, pp. 26 ( online ).
- ^ Robert Plato: Numerical Mathematics compact . 4th edition. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , pp. 171-173 .
- ↑ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerics of ordinary differential equations . 2nd Edition. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , p. 57-59 .
- ^ Peter Deuflhard, Folkmar Bornemann: Numerical Mathematics 2 - Ordinary Differential Equations . 3. Edition. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , p. 199-204 .
- ^ Robert Plato: Numerical Mathematics compact . 4th edition. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , chap. 7: One-step method for initial value problems , p. 173-177 .
- ↑ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerics of ordinary differential equations . 2nd Edition. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , p. 64-70 .
- ↑ ode45: Solve nonstiff differential equations - medium order method. MathWorks, accessed November 23, 2017 .





















































![{\ displaystyle I = [t_ {0}, T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2831dbc758b56a055d906e2728089c3041398e4)














































































![{\ displaystyle [0.20]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83fa6e3e4170f0b2c00d850bc56487657407968e)


