Escape speed (space travel)
When the escape or escape speed is reached, the kinetic energy of a test body is just sufficient to escape the gravitational potential of a celestial body without any further propulsion - ballistically . Tabulated values mostly refer to the surface of celestial bodies as a starting point. The air friction and the speed contribution due to the rotation of the celestial body and contributions of other bodies to the gravitational potential are not taken into account; they must of course be observed in practice. In simple terms, the escape speed depends on a celestial body assumed to be spherically symmetrical , according to the shell theorem, only on its mass and radius .
The escape speed from the earth is also called the second cosmic speed - the first is the orbit speed in the low orbit around the earth. The concept of cosmic speed with the meaning of very high speed originated in the middle of the 19th century in connection with meteors . At the time of the race to the moon , the cosmic speeds were sometimes also called astronautical .
Orbital velocity
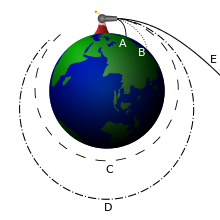
With the 1st cosmic speed the body describes a circular orbit around the earth and becomes a satellite (C), with a slightly higher speed an elliptical orbit is reached (D).
With the second cosmic speed of the spacecraft the orbit opens to a Kepler parabola (E).
When a body moves at speed on a circular orbit with a radius around the center of the earth (or another celestial body), its centripetal acceleration is . In free fall it is caused exclusively by the gravity of the planet, so:
Here is the gravitational constant and the mass of the planet. The circular path speed is obtained by rearranging the above equation:
For the earth is 3.986 · 10 14 m 3 / s 2 and the mean radius is 6371 km. Thus, the circular path velocity as the first cosmic velocity to = 7.91 km / s. This value is of no practical importance, since such speeds cannot be maintained within the earth's atmosphere. The missile would be strongly decelerated by the air resistance and destroyed by the resulting heat.
At an altitude of around 180 km, i.e. at the limit of the earth's atmosphere , the orbit speed is around 7.8 km / s.
The local rotation speed of the earth also plays a role in a rocket launch, since it can reduce the speed to be generated by the rocket. This effect is maximal when starting at the equator in an easterly direction. Under this condition the earth's rotation makes a contribution of about 0.46 km / s.
Escape speed
| Heavenly bodies |
at the equator in km / s |
|---|---|
| Mercury | 4.3 |
| Venus | 10.2 |
| earth | 11.2 |
| moon | 2.3 |
| Mars | 5.0 |
| Phobos | 0.011 |
| Deimos | 0.006 |
| Ceres | 0.5 |
| Jupiter | 59.6 |
| Saturn | 35.5 |
| Uranus | 21.3 |
| Neptune | 23.3 |
| Pluto | 1.1 |
| Sun | 617.4 |
| Sun at a distance from the earth |
42.1 |
| Event horizon of a black hole |
light speed |
The escape speed is the minimum speed for an open, non-return path. The kinetic energy of a specimen is then equal to its binding energy in the gravitational field , i.e.:
Change to results in:
The escape speed is therefore higher by a factor than the first cosmic speed.
For celestial bodies with constant mean density and radius scaled with , i.e. linear with . The table opposite contains examples.
Alternative calculation of the escape speed from the surface gravitational acceleration g and the radius of the object without taking into account the rotational speed of the object:
In the value 11.2 km / s for the earth, the second cosmic speed , the rotation speed of the earth is again not taken into account. The escape speed does not have to be reached completely for flight paths to the moon , because L1 is not included .
Conversely, one can also deduce from the speed that a body (without any noteworthy propulsion of its own) has when it reaches the earth, at which distance the body began to accelerate towards earth (although one can change the speed of the earth on its orbit must take into account the sun): During the Apollo missions , the speed at re-entry was 10.8 km / s. In the case of the Apollo mission, a value higher (or equal to) than 11.2 km / s would not be possible, since otherwise the space capsule would have had to "run up" from a much greater distance (namely ). With this approach one can therefore also narrow down the “origin” of comets or meteorites. Example: The escape speed (from the sun) on the earth's orbit is about 42 km / s, the speed of the earth itself about 30 km / s. All bodies that orbit the sun within the solar system can reach a maximum speed of (42 + 30 =) 72 km / s in a frontal impact with the earth. Bodies that are even faster in this impact scenario must therefore originally have come from outside the solar system.
Geometric meaning
When a missile that is on a circular path around a planet receives a speed boost in the direction of flight, its flight path is deformed into an ellipse . If the speed is increased further, the eccentricity of the ellipse increases. This goes on until the distant focus of the ellipse is infinitely far away. From this speed the body is no longer on a closed path, but the ellipse opens to a parabolic path . This happens exactly when the missile reaches the second cosmic speed.
As the body moves away from the planet, it continues to be slowed down by its gravitation, so that it only comes to a standstill at an infinite distance. If, on the other hand, the second cosmic speed is exceeded, the trajectory takes on the form of a hyperbolic branch - in this case a speed remains at infinity, which is called hyperbolic excess speed or hyperbolic excess speed and characterizes the energy of the hyperbolic orbit. It is calculated from the sum of the energies, i.e. the squares of the speeds, analogous to the calculation in the following section. It is also common to specify the square of the speed (i.e. energy per mass), often with the symbol c 3 .
Escape speed from a black hole
In the general theory of relativity , the radial escape velocity is calculated as according to Newton, but is direction-dependent. In addition, the orbit speed is higher than according to Newton, by the factor with . Only with increasing distance from the center of gravity does the ratio of escape and circular orbit speed converge . The reason for this is that in the gravitational field the space is not Euclidean and the circumference of a circle is less than . While the escape speed only reaches the speed of light at the event horizon of the black hole at , the orbit speed is already at (at the so-called photon sphere) the same and up to greater than the radial escape speed.
Escape speeds from other objects
The third cosmic speed is the minimum take-off speed from the earth's surface, with which the solar system can be left (if the earth's orbital speed around the sun is used, but without using its own rotation and without swing-by maneuvers on planets). The missile has to overcome the common gravitational field of the earth and the sun. After starting at = 11.2 km / s and leaving the Earth's sphere of influence , the body still has the hyperbolic excess speed . Together with the orbital speed of the earth, this must result in the escape speed from the solar system at a distance = 1 AU ,
- .
The starting speed required to achieve this speed is then derived from
or.
- .
The mass of the moon and the other planets has been neglected here; the result would hardly change.
In the case of the escape speed from the Milky Way , however, the gravitational field is very clearly not a central field and a considerable part of the mass lies outside the orbit of the sun around the galactic center. A numerical calculation, which also takes into account a model for the distribution of dark matter , results in an escape speed of . As expected, this is far more than times the orbital speed of the sun of around 220 km / s.
See also
swell
- Cosmic Velocities ( LEIFI Physics)
Individual evidence
- ^ Giovanni Virginio Schiaparelli : Draft of an astronomical theory of falling stars . 1867, translation from Italian 1871, limited preview in Google Book search, digital version of the original.
- ↑ Karl Böhm, R. Dörge: On the way to distant worlds: a book from space travel. Neues Leben, Berlin, 1958, p. 89.
- ↑ For the value of 42.1 km / s it should be noted: if a satellite / specimen / particle starts from the sun's surface with the local escape speed of 617.4 km / s, it has when it reaches the earth's orbit around the sun the remaining speed of 42.1 km / s, which is still necessary from this distance to leave the solar system. But if the satellite starts from earth orbit, it already has the orbit speed of the earth of 29.8 km / s, and a lower start speed is necessary in particular relative to the earth. See section # Escape velocities from other objects for more details.
- ^ Rosswog and Bruggen: High Energy Astrophysics . ASTR 498 @ University of Maryland, PDF, p. 7.
- ↑ Ernst Messerschmid, Stefanos Fasoulas: Space systems - an introduction with exercises and solutions. Springer-Verlag, 2000, ISBN 978-3-662-09675-8 , pp. 106-109 ( limited preview in the Google book search).
- ^ Til Piffl et al .: The RAVE survey: the Galactic escape speed and the mass of the Milky Way . Astronomy & Astrophysics 562, 2014, doi: 10.1051 / 0004-6361 / 201322531 (free full text).
- ↑ MJ Reid, ACS Readhead, RC Vermeulen, RN Treuhaft: The Proper Motion of Sagittarius A *. I. First VLBA Results . In: The Astrophysical Journal . tape 524 , no. 2 , 1999, p. 816–823 , doi : 10.1086 / 307855 , bibcode : 1999ApJ ... 524..816R .

































