Minimal area

A minimal area is an area in space that has a locally minimal area . Such shapes take, for example, soap skins when they are stretched over an appropriate frame (such as a blow ring).

In mathematical terms, minimal areas are the critical points of the area functional

${\displaystyle A(\mathbf {x} )=\int {\sqrt {g(u)}}\,\mathrm {d} ^{n}u}$.

Here are the sizes and for stated (see. Hessian matrix ). Note that a minimal area does not necessarily have a minimal area, but is just a stationary point of the area functional. It can be shown that the vanishing of the first variation of the area functional in two spatial dimensions is equivalent to the vanishing of the mean curvature H if the manifold under consideration is sufficiently regular. ${\displaystyle g(u):=\operatorname {det} (g_{ij}(u))_{i,j=1,\dotsc ,n}}$ ${\displaystyle g_{ij}(u)=\left({\tfrac {\partial \mathbf {x} }{\partial u_{i}}}\right)^{T}{\tfrac {\partial \mathbf {x} }{\partial u_{j}}}}$ ${\displaystyle i,j=1,\dotsc ,n}$

Mathematical research has been focusing on minimal areas since the 19th century. The experiments of the Belgian physicist Joseph Plateau made a significant contribution to this .

Enneper area as an example of a minimal area

Explanations on existential theory in two variables

A two-dimensional parameter area always represents a specialty. Because with the tools of the function theory one can achieve much more extensive statements than in higher spatial dimensions. This means, for example, that you can always use the circular disk as a parameter area with Riemann's theorem of mapping . The uniformity theorem only applies in two spatial dimensions. It enables isothermal parameters to be introduced, which are required for the solution in the parametric case. That is why the theory is particularly well developed in two variables.

Formulation as a problem of variation

A surface is a minimum surface if and only if it has zero mean curvature at every point . A minimum surface is thus a special case of a surface with prescribed mean curvature. These are also not withdrawn from the calculus of variations , they are minima of Hildebrandt's functional

${\displaystyle A(\mathbf {x} )=\iint {\big (}|\mathbf {x} _{u}\times \mathbf {x} _{v}|+2(Q(\mathbf {x} ),\mathbf {x} _{u},\mathbf {x} _{v}){\big )}\,\mathrm {d} u\,\mathrm {d} v}$.

Euler's equations as the necessary minimum conditions of this functional are the H-surface system named after Franz Rellich

${\displaystyle \Delta \mathbf {x} =2H\mathbf {x} _{u}\times \mathbf {x} _{v},\qquad \mathbf {x} _{u}^{2}-\mathbf {x} _{v}^{2}=0=\mathbf {x} _{u}\mathbf {x} _{v}}$.

Here is the mean curvature. ${\displaystyle H=\operatorname {div} \,Q}$

Parametric case

For this functional, the question arises of the existence of local minima given a given continuous boundary curve of finite length. This task is also referred to in the literature as Plateau's problem. Assuming a smallness condition for the mean curvature, which is always fulfilled in the case of the minimum area, this question can be answered positively. To convince yourself of this, one minimizes and the energy functional at the same time ${\displaystyle A}$

${\displaystyle E(\mathbf {x} )=\iint {\Big (}{\frac {1}{2}}|\nabla \mathbf {x} |^{2}+2(Q(\mathbf {x} ),\mathbf {x} _{u},\mathbf {x} _{v}){\Big )}\,\mathrm {d} u\,\mathrm {d} v}$

with the introduction of so-called almost isothermal parameters.

In 1884 Herrmann Amandus Schwarz proved the sentence

In the set of continuously differentiable , simply closed, orientable surfaces of gender zero (i.e. without holes), the sphere is the surface that delimits the largest volume for a given surface.

Branch points

Points where the solution satisfies are called branch points. Branch points are interesting because the parameterization can become singular at these points . Even worse is the possibility that the local solution is no longer a surface, but just a curve. ${\displaystyle |\mathbf {x} _{u}\times \mathbf {x} _{v}|=0}$

Function-theoretical considerations, which are essentially inspired by the work of Carleman and Vekua , show that the solution can at most have a finite number of such branch points. Unfortunately, the above method does not exclude such branch points a priori. Only with the elaborate sentence by Gulliver-Alt- Osserman does this succeed a posteriori. Therefore there is a desire to solve the plateau problem in the class of H-surfaces without branching points. This is still an open question today.

Non-parametric case, minimum area equation

The above method only leads to success for constant ones. If the mean curvature also depends on the solution, something can still be done in the case of a graph : If a graph is, it is written as and the function fulfills the nonparametric equation of prescribed mean curvature ${\displaystyle H}$ ${\displaystyle \mathbf {x} }$ ${\displaystyle \mathbf {x} (u,v)=(u,v,\zeta (u,v))^{T}}$ ${\displaystyle \zeta }$

${\displaystyle (1+\zeta _{v}^{2})\zeta _{uu}-2\zeta _{u}\zeta _{v}\zeta _{uv}+(1+\zeta _{u}^{2})\zeta _{vv}=H(u,v,\zeta (u,v))}$.

In the case of minimal areas, H = 0 and the equation is called the minimal area equation.

The solvability of the Dirichlet problem of this partial differential equation also provides a deep-seated existence result under the assumption of a smallness condition and further technical requirements. The uniqueness is also clarified by a maximum principle for the difference between two solutions. In addition, graphs are due to

${\displaystyle |\mathbf {x} _{u}\times \mathbf {x} _{v}|={\sqrt {1+\nabla \zeta (u,v)^{2}}}\geq 1}$

always free of branch points.

Examples of minimal areas

Several examples of the most varied minimal areas in three-dimensional Euclidean space are given here. Some of them cannot be embedded in three-dimensional space without self-cuts. Others cannot be continued continuously to the edge of their domain, as the first example shows.

The minimum area of ​​HF Scherk

Related component of Scherk's minimum area to parameter c = 1

The minimal area by Heinrich Ferdinand Scherk (1835): We are looking for all solutions to the nonparametric minimal area equation that can be written in the form and that satisfy the conditions . We first insert this structure into the minimum area equation and get: ${\displaystyle z=\zeta {\big (}u,v{\big )}=f(u)+g(v)}$ ${\displaystyle \zeta {\big (}0,0{\big )}=0}$ ${\displaystyle \nabla \zeta (0,0)=0}$

${\displaystyle 0\,\,=(1+\zeta _{v}^{2})\zeta _{uu}-2\zeta _{u}\zeta _{v}\zeta _{uv}+(1+\zeta _{u}^{2})\zeta _{vv}}$

${\displaystyle ={\big (}1+(g'(v))^{2}{\big )}f''(u)+(1+(f'(u))^{2})g''(v)}$

Equivalent conversion provides

${\displaystyle -{\frac {f''(u)}{1+(f'(u))^{2}}}=c={\frac {g''(v)}{1+(g'(v))^{2}}}}$

with one . According to the theory of ordinary differential equations, there is exactly one solution for each of the initial value problems ${\displaystyle c\in \mathbb {R} }$

${\displaystyle f''{\big (}u{\big )}+c(1+(f'(u))^{2})=0}$ to the data ${\displaystyle f(0)=0,\,\,f'(0)=0}$

and

${\displaystyle g''{\big (}v{\big )}-c(1+(g'(v))^{2})=0}$ to the data ${\displaystyle g(0)=0,\,\,g'(0)=0.}$

These solutions are

${\displaystyle f(u)={\frac {1}{c}}\log \cos(cu)}$

and

${\displaystyle g(v)=-{\frac {1}{c}}\log \cos(cv).}$

several connected components of the Scherk's minimum surface for the parameter c = 0.2

It remains to be noted here that we could still vary the initial values and with one . However, oBdA can be required because of the structural condition and the fact that the functions themselves do not appear in the ordinary differential equations . So we get: ${\displaystyle f{\big (}0)=d}$ ${\displaystyle g{\big (}0)=-d}$ ${\displaystyle d\in \mathbb {R} }$ ${\displaystyle d=0}$

${\displaystyle z=\zeta {\big (}u,v{\big )}=f(u)+g(v)={\frac {1}{c}}\log {\frac {\cos(cu)}{\cos(cv)}}}$

We notice that this minimal area is on the squares

${\displaystyle \Omega :={\big \{}(u,v)\in \mathbb {R} ^{2}:\,{\big |}u+k{\frac {\pi }{c}}{\big |}<{\frac {\pi }{2c}},{\big |}v+l{\frac {\pi }{c}}{\big |}<{\frac {\pi }{2c}}\quad {\text{für}}\quad k,l\in \mathbb {Z} \quad {\text{mit}}\quad k\equiv l{\pmod {2}}{\big \}}}$

and cannot be continued beyond that. This area can be embedded as a graph in the three-dimensional space.

The catenoid

Catenoid for parameter c = 1

If you let the chain line rotate around the x-axis, you also get a minimal area embedded in three-dimensional space - a catenoid. Catenoids are the only minimal surfaces that are also surfaces of revolution at the same time. They are sufficient for a positive parameter c> 0 of the equation

${\displaystyle {\sqrt {x^{2}+y^{2}}}=c\,\operatorname {cosh} {\frac {z}{c}}.}$

It was one of Plateau's first experimental solutions to the Plateau problem. Here the edge data were two circular rings, which form the upper and lower edge curve of a truncated cone or cylinder.

The catenoid as a minimal surface comes from Leonhard Euler around 1740.

The helical surface

Helicoid for parameter c = 1

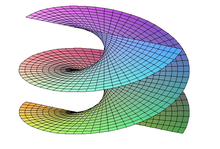
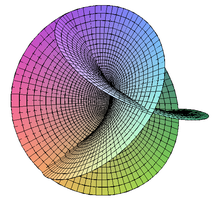
→ Main article : helical surface

The helical surface or the helicoid is closely related to the catenoid. This surface emerges from a catenoid through a discontinuous but isometric deformation. For a parameter c> 0 it satisfies the following equations:

${\displaystyle x{\big (}u,v)=u\cos v}$

${\displaystyle y{\big (}u,v)=u\sin v}$

${\displaystyle z{\big (}u,v)=cv}$

This minimal area is also embedded in the three-dimensional space.

The spiral surface as a minimal surface comes from Jean-Baptiste Meusnier de la Place (1776). The helicoids have the topological gender 0. In the 1990s, David Allen Hoffman and colleagues constructed complete minimal surfaces with infinite and arbitrary finite topological gender that could be embedded in three-dimensional Euclidean space with the aid of a computer , whereby the strict proof only for infinite gender and for gender 1 ( Michael Wolf , Hoffman, Matthias Weber 2009). For genus 0, the helicoids (which also includes the catenoids as a special case) and the plane are the only completely embeddable minimal surfaces ( William Meeks , Harold William Rosenberg 2005).

The Henneberg area

Henneberg's minimal surface

The Henneberg surface is an example of a minimal surface which is the image of an immersion in the three-dimensional Euclidean space but cannot be embedded in the three-dimensional Euclidean space. Their determining equations are:

${\displaystyle x(u,v)=2\sinh u\cos v-{\frac {2}{3}}\sinh(3u)\cos(3v)}$

${\displaystyle y(u,v)=2\sinh u\sin v+{\frac {2}{3}}\sinh(3u)\sin(3v)}$

${\displaystyle z(u,v)=2\cosh(2u)\cos(2v)}$

In addition, this surface cannot be orientated: In clear terms, one cannot decide which side of this surface is up and which is down .

It is named after Lebrecht Henneberg , who introduced it in his dissertation in 1875.

Higher room dimensions

In large spaces, access to the plateau problem is difficult to imagine. Here you only have the option of viewing the solution as a graph. The minimum area equation for the graph is written

${\displaystyle \operatorname {div} {\frac {\nabla \zeta }{\sqrt {1+\nabla \zeta ^{2}}}}=0}$.

With the theory of weak solvability of elliptic boundary value problems one can guarantee the existence of solutions in this situation as well. The following regularity considerations provide a classic solution. As in two spatial dimensions, the uniqueness is also obtained here through a maximum principle for the difference between two solutions.

Some interesting statements about minimal areas

Due to the relatively simple structure of the equations, which are satisfied by minimal areas, one can transfer some well-known statements, which are especially known for holomorphic or harmonic functions, to minimal areas in two variables.

Maximum principle

The inequality holds for a minimal area ${\displaystyle \mathbf {x} }$

${\displaystyle \sup _{w\in B}|\mathbf {x} (w)|\leq \sup _{w\in \partial B}|\mathbf {x} (w)|}$.

The minimum area therefore assumes its maximum on the edge of the area on which it is declared.

Uniformizing images

So-called isothermal parameters can be introduced in geodesy. The mapping that accomplishes this is called uniformizing mapping. Uniformizing images of minimal surfaces are harmonious functions .

Real analytical character

As long as they are present in isothermal parameters, minimal areas are real analytical functions in the interior of the area in which they are explained. This means that the parametric representation can be expanded into a convergent power series at any point in the area in the vicinity of this point . Therefore it can be differentiated any number of times . If, in addition, the boundary curve is real analytical at a point, then the minimum area in the vicinity of this point can be continued beyond the edge using real analysis.

The theorems of Bernstein and Liouville

Sergei Bernstein's theorem for minimal surfaces is:

A fully explained solution of the non-parametric minimum area equation necessarily satisfies the equation ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \zeta {\big (}u,v{\big )}}$

${\displaystyle \zeta {\big (}u,v{\big )}=au+bv+c}$

with constants . ${\displaystyle a,b,c\in \mathbb {R} }$

The question of generalization to higher dimensions is known as the problem of Bernstein and was solved by Ennio de Giorgi , Enrico Bombieri and others.

From this theorem, Liouville's theorem for minimal surfaces immediately follows :

A solution of the nonparametric minimal area equation that is limited to a completely explained one is necessary ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \zeta {\big (}u,v{\big )}}$

${\displaystyle \zeta {\big (}u,v{\big )}=\operatorname {const} }$.

This is an analogue of Liouville's theorem of function theory.

The area of ​​a minimal area

The area of ​​a minimal area with the unit normal is written in the form ${\displaystyle \mathbf {x} }$ ${\displaystyle \mathbf {n} }$

${\displaystyle A=\oint (\mathbf {n} ,\mathbf {x} ,\mathrm {d} \mathbf {x} )}$.

It must be assumed that the boundary curve is simply closed and continuously differentiable.

Representation formulas

In order to better understand minimal areas, it is not enough to only consider the differential equations that they satisfy, but one should also determine special representations of the solution.

Complex representation

Introducing isothermal parameters u and v, we first get the H-surface system for H = 0:

${\displaystyle \Delta \mathbf {x} =0,\qquad \mathbf {x} _{u}^{2}-\mathbf {x} _{v}^{2}=0=\mathbf {x} _{u}\mathbf {x} _{v}}$

The equation of the second order is thus written in the form

${\displaystyle {\frac {\partial ^{2}\mathbf {x} }{\partial z^{1}\partial z^{2}}}=0}$

with the complex variables and and we get the representation ${\displaystyle z^{1}=u+iv}$ ${\displaystyle z^{2}=u-iv}$

${\displaystyle 2\mathbf {x} =\mathbf {y} (z^{1})+\mathbf {z} (z^{2})\qquad }$and . ${\displaystyle \qquad (\mathbf {y} ')^{2}=0=(\mathbf {z} ')^{2},\qquad \mathbf {y} '\mathbf {z} '\neq 0}$

We call a complex curve that satisfies the conditions and an isotropic curve. We also call an area that can be written in the form a sliding area . ${\displaystyle \mathbf {y} (z)}$ ${\displaystyle (\mathbf {y} ')^{2}=0}$ ${\displaystyle \mathbf {y} '\neq 0}$ ${\displaystyle \mathbf {x} (u,v)}$ ${\displaystyle \mathbf {x} (u,v)=\mathbf {y} (u)+\mathbf {z} (v)}$

A generalized definition of minimal areas is:

A minimal surface is a sliding surface whose generators are isotropic curves.

Real minimal areas then meet the conditions

${\displaystyle {\overline {z^{1}}}=z^{2}\qquad }$and . ${\displaystyle \qquad \mathbf {z} ({\overline {z^{1}}})={\overline {\mathbf {y} (z_{1})}}}$

Integral representation

→ Main article : Enneper-Weierstrasse construction

The representation formula named after Karl Weierstrass and Alfred Enneper provides a connection between differential geometry and function theory . Now Weierstrass had a great influence on the development of the theory of functions. This representation formula was one of the reasons why this relatively new branch of mathematics was taken seriously and was and is so successful. He found out that every non-constant minimal surface can be written as an integral with the two holomorphic functions g and h. The following applies to the components: ${\displaystyle \mathbf {x} (w)={\big (}x(w),y(w),z(w){\big )}}$

${\displaystyle x(w)=c_{1}+\operatorname {Re} \int _{w_{0}}^{w}{\frac {h(\zeta )\left(1-g(\zeta )^{2}\right)}{2}}\mathrm {d} \zeta }$,

${\displaystyle y(w)=c_{2}+\operatorname {Re} \int _{w_{0}}^{w}{\frac {h(\zeta )\left(1+g(\zeta )^{2}\right)}{2}}\mathrm {d} \zeta }$,

${\displaystyle z(w)=c_{3}+\operatorname {Re} \int _{w_{0}}^{w}h(\zeta )g(\zeta )\mathrm {d} \zeta }$

This representation formula makes it possible to generate images of any minimal surface with the help of modern computer algebra systems. For example, some images of minimal surfaces in this article were created using these formulas with the Maple program.

Integral-free representation

Since we have seen that in order to integrate the differential equation H = 0, it is sufficient to determine isotropic curves, we obtain the so-called integral-free representation for real minimal areas ${\displaystyle \mathbf {x} (w)={\big (}x(w),y(w),z(w){\big )}}$

${\displaystyle x(w)=\operatorname {Re} \left(\pm i\left(f(w)-wf'(w)-{\frac {1-w^{2}}{2}}f''(w)\right)\right)}$

${\displaystyle y(w)=\operatorname {Re} \left(f(w)-wf'(w)+{\frac {1+w^{2}}{2}}f''(w)\right)}$

${\displaystyle z(w)=\operatorname {Re} \left(-i{\big (}f'(w)-wf''(w){\big )}\right)}$

with a holomorphic function that must meet the requirement. Levels thus elude this representation. In order to clarify the meaning of the complex variables for a real minimal area, we provide a lengthy calculation ${\displaystyle f=f(w)}$ ${\displaystyle f'''\neq 0}$ ${\displaystyle w}$

${\displaystyle w={\frac {n_{1}+in_{2}}{-1+n_{3}}}}$or , ${\displaystyle {\frac {1}{w}}={\frac {n_{1}+in_{2}}{-1+n_{3}}}}$

here is the unit normal vector of the minimum area. We summarize: By specifying the complex number or the unit normal vector of the minimum area is determined. Conversely, or only depends on . The statements in this section can be found in the book Elementare Differentialgeometrie by W. Blaschke and K. Leichtweiß, see also literature . ${\displaystyle \mathbf {n} =(n_{1},n_{2},n_{3})}$ ${\displaystyle w}$ ${\displaystyle 1/w}$ ${\displaystyle \mathbf {n} }$ ${\displaystyle w}$ ${\displaystyle 1/w}$ ${\displaystyle \mathbf {n} }$

Notes on the area functional

We will first derive this functional in general and show the invariance under positively oriented parameter transformations . Finally, we will explicitly calculate the one- and two-dimensional special cases.

Derivation and parameter invariance

We note that our minimal area can be understood as an m-dimensional manifold in the n-dimensional real vector space. This is always possible due to Nash's embedding theorem . We first explain the metric tensor

${\displaystyle g_{ij}(u):={\frac {\partial \mathbf {x} (u)}{\partial u_{i}}}{\frac {\partial \mathbf {x} (u)}{\partial u_{j}}}}$

with the determinant

${\displaystyle g(u):=\operatorname {det} (g_{ij}(u))_{i,j=1,\dotsc ,m}}$.

We remember that the content of an m-dimensional area results as an m-dimensional integral over the characteristic function of this area. A characteristic function is identically one everywhere in the set and otherwise identically zero. With that we just have to express the UI element appropriately. We explain the tangent vectors at a fixed point u

${\displaystyle {\frac {\partial \mathbf {x} (u)}{\partial u_{i}}}}$ For ${\displaystyle i,j=1,\dotsc ,m}$

and choose vectors such that the system ${\displaystyle \xi _{m+1},\dotsc ,\xi _{n}}$

${\displaystyle (\mathbf {x} _{u_{1}},\dotsc ,\mathbf {x} _{u_{m}},\xi _{m+1},\dotsc ,\xi _{n})}$

is positively oriented and fulfills the two conditions and for all meaningful values ​​of i and j. The UI element is thus written: ${\displaystyle (\mathbf {x} _{u_{i}},\xi _{j})=0}$ ${\displaystyle {\big (}\xi _{i},\xi _{j})=\delta _{ij}}$

${\displaystyle {\begin{aligned}\mathrm {d} \sigma (u)&=\operatorname {det} (\mathbf {x} _{u_{1}},\dotsc ,\mathbf {x} _{u_{m}},\xi _{m+1},\dotsc ,\xi _{n})\mathrm {d} u_{1}\dotsm \mathrm {d} u_{m}\\&={\sqrt {\operatorname {det} ((\mathbf {x} _{u_{1}},\dotsc ,\xi _{n})^{T}(\mathbf {x} _{u_{1}},\dotsc ,\xi _{n}))}}\mathrm {d} u_{1}\dotsm \mathrm {d} u_{m}\\&={\sqrt {\operatorname {det} (g_{ij}(u))_{i,j=1,\dotsc ,m}}}\mathrm {d} u_{1}\dotsm \mathrm {d} u_{m}\\&={\sqrt {g(u)}}\mathrm {d} u_{1}\dotsm \mathrm {d} u_{m}\end{aligned}}}$

For the determinant of two matrices with : ${\displaystyle m\times n}$ ${\displaystyle m\leq n}$

${\displaystyle \operatorname {det} (A^{T}B)=\sum _{1\leq i_{1}<\dotsb <i_{m}\leq n}\operatorname {det} A_{i_{1}\dotso i_{m}}\operatorname {det} B_{i_{1}\dotso i_{m}}}$

This denotes that sub-matrix of which only consists of the rows . With this we can change the UI element in the form ${\displaystyle A_{i_{1}\dotso i_{m}}}$ ${\displaystyle A}$ ${\displaystyle i_{1},\dotsc ,i_{m}}$

${\displaystyle \mathrm {d} \sigma (u)={\sqrt {\sum _{1\leq i_{1}<\dotsb <i_{m}\leq n}\left({\frac {\partial {\big (}\mathbf {x} _{u_{i_{1}}},\dotsc ,\mathbf {x} _{u_{i_{m}}}{\big )}}{\partial {\big (}u_{1},\dotsc ,u_{m}{\big )}}}\right)^{2}}}\mathrm {d} u_{1}\dotsm \mathrm {d} u_{m}}$

write. With the help of the transformation formula , we now determine the invariance under the same-direction parameter transformations of the surface element and thus of the area functional.

The one and two dimensional content

In one room dimension, this functional is reduced to the usual path length :

${\displaystyle A(\mathbf {x} )=\int |\mathbf {x} '(u)|\,\mathrm {d} u}$

If you have a two-dimensional surface that is embedded in the three-dimensional space, you get with the identity of Lagrange :

${\displaystyle EG-F^{2}=|\mathbf {x} _{u}\times \mathbf {x} _{v}|^{2}}$

The following applies to the area functional:

${\displaystyle A(\mathbf {x} )=\iint |\mathbf {x} _{u}\times \mathbf {x} _{v}|\,\mathrm {d} u\mathrm {d} v}$

literature

• Wilhelm Blaschke , Kurt Leichtweiß: Elementary differential geometry (= basic teachings of the mathematical sciences. Volume 1). Springer-Verlag, 1973, online.
• Johannes CC Nitsche : Lectures on minimal areas (= basic teachings of the mathematical sciences. Volume 199). Springer-Verlag, 1975.
• David Gilbarg , Neil Trudinger : Elliptic Partial Differential Equations of Second Order (= basic teachings of the mathematical sciences. Volume 224). Springer-Verlag, 1983.
• Ullrich Dierkes, Stefan Hildebrandt , Albrecht Küster, Ortwin Wohlrab: Minimal Surfaces (= basic teachings of the mathematical sciences. Volumes 295 and 296). Springer-Verlag, 1992, 2 volumes.
• Stefan Hildebrandt, Anthony Tromba: Sphere, circle and soap bubbles, optimal forms in geometry and nature. Birkhäuser, 1996.
• Friedrich Sauvigny : Partial differential equations of geometry and physics. Springer-Verlag, 2004 f., 2 volumes.

Web links

Commons : Minimal areas  - collection of images, videos and audio files

• Eric W. Weisstein : Minimal Surfaces . In: MathWorld (English).
• Popular scientific article from the spectrum of science
• Graphic introduction to minimal areas
• Triple periodic minimal surfaces
• 3D-XplorMath: Program for Mac or Java with many families of minimal areas

Individual evidence

1. ^ Minimal surfaces , Mathworld
2. ^ Mathworld, Henneberg minimal surface