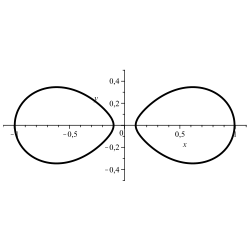
oval

The title of this article is ambiguous. Further meanings are listed under Oval (disambiguation) .

Oval with an axis of symmetry

The term oval ( Latin ovum , egg) denotes a flat, rounded convex figure that, in the broadest sense, resembles the profile of a bird's egg . It includes circles and ellipses as special cases, whereby any oval, in contrast to these, does not have to have an axis of symmetry .

The use of the term is not always completely uniform; it is occasionally used purely for descriptive purposes. In analysis , however, it can be formally defined with the help of flat curves , in this context one also speaks of egg curves or egg lines .

A three-dimensional round convex body (more generally also a closed convex subset of the ) is called an ovoid . In this sense, an oval with its interior is then a two-dimensional ovoid. ${\displaystyle \mathbb {R} ^{n}}$

In projective geometry , the terms oval and ovoid without differentiability and convexity conditions are defined as square sets exclusively with the help of incidence conditions (“Every straight line meets an oval or ovoid in at most 2 points”) . An oval, as it is explained in the present article, is always an oval in the projective closure of the real plane in the sense of the projective definition, if one additionally demands that the curvature of the oval does not disappear on any section. Such an oval is then the edge of a strictly convex set , i.e. i.e. it does not contain any straight lines .

Formal definition and properties

Oval without axes of symmetry

The rounded shape of an oval is obtained by demanding smoothness and convexity for a closed curve . This then leads to the following definition:

A closed, twice continuously differentiable convex curve in the plane is called an oval (also an egg curve or egg line ).

However, this definition does not cover all geometric figures, which are sometimes referred to as ovals. For example, ovals that are composed of different arcs do not meet this definition because their second derivative is not continuous on the entire curve. If you want to cover such cases, you have to compromise on the smoothness of the curve ( differentiation class or instead ). Occasionally, therefore, only the convexity is required. However, this has the disadvantage that the definition then also includes figures that are normally hardly perceived as "egg-shaped", such as convex polygons . ${\displaystyle C^{0}}$ ${\displaystyle C^{1}}$ ${\displaystyle C^{2}}$

An oval as defined above has the following properties:

Oval with tangent, secant and passer-by

• An oval is a Jordan curve ; that is, it has no loops or loops.
• The oriented curvature of an oval has no change in sign , i. i.e., depending on the direction of passage, the oriented curvature for each point on the oval is either non-negative or non-positive. This clearly means that it has no turns or indentations. You can only go through it in a pure left turn or right turn.
• The inside of an oval is a convex set, and the oval forms its edge.
• The four-vertex theorem applies to ovals , that is, the curvature of an oval has at least four extreme points.
• If a point of the oval has a tangent , the entire oval is on one side of the tangent.
• If one additionally demands that the curvature of the oval does not disappear on any section, that is, the curvature takes on the value zero at most in isolated points, then the above tangent exists at every point of the oval. More generally, it then applies to any straight line that it has either no point ( passer-by ), exactly one point (tangent) or exactly two points ( secant ) in common with the oval .

Examples and constructions

Ovals can be constructed using completely different methods. A number of construction methods are obtained from the various construction methods for ellipses, each of which is slightly modified at an appropriate point.

You can create an ellipse by intersecting a cone with a plane (see conic sections ). If, instead of the cone, certain other bodies of revolution are used, for example a rotated hyperbola , then one obtains ovals other than ellipses in a section with a plane. Another possibility is to replace the constant parameters and (lengths of the semi-axes) of an ellipse in its parametric representation or in its algebraic equation with functions. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle (a\cdot \cos(t),b\cdot \sin(t))}$ ${\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1}$

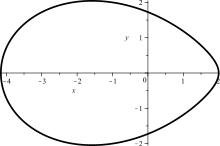
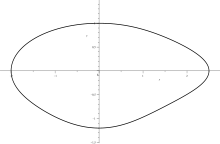
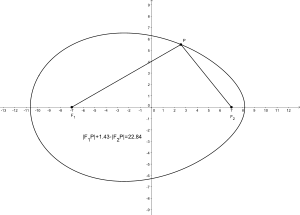
An ellipse can be defined as the set of points for which the sum of the distances to the two focal points and is constant . If this sum of the distances is now replaced by a weighted sum , the point set forms an oval that has only one axis of symmetry on which a pointed and a blunt end lie. Such an oval is also known as a Cartesian oval . ${\displaystyle P}$ ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$ ${\displaystyle \left(|F_{1}P|+|F_{2}P|=2a\right)}$ ${\displaystyle \left(k_{1}\cdot |F_{1}P|+k_{2}\cdot |F_{2}P|=2a\right)}$

The construction process of de La Hire creates an ellipse with the help of two concentric circles . If you move the center of the outer circle a little and otherwise keep the remaining steps of the construction process, you get a (new) oval. This has an axis of symmetry if you move the center of the outer circle along the axis of the ellipse. If you move the center point outside of the axes, an oval is created without axes of symmetry.

• 

  Construction with concentric circles

• 

  Construction with eccentric circles

• 

  Ellipse: ${\displaystyle |F_{1}P|+|F_{2}P|=22{,}84\,}$

• 

  ${\displaystyle |F_{1}P|+{\textbf {1.43}}\cdot |F_{2}P|=22{,}84}$

• 

  Ellipse: ${\displaystyle {\frac {x^{2}}{4}}+{\frac {y^{2}}{1}}=1}$

• 

  ${\displaystyle {\frac {x^{2}}{4}}+{\frac {y^{2}}{1-0{,}2\cdot x}}=1}$

The solution set of an equation with two unknowns or certain subsets of it can often be understood as curves in the plane. With a suitable equation, you get an oval. If such a solution curve is not an oval, but has a convex loop, an oval can be created from the loop by adding a correction term.

• 

  Elliptic curve : ${\displaystyle y^{2}=(x-1)\cdot (x-2)\cdot (x-3)}$

• 

  Lamé oval : ${\displaystyle \left({\frac {x}{2}}\right)^{4}+\left({\frac {y}{1}}\right)^{4}=1}$

• 

  Lemniscates : ${\displaystyle (x^{2}+y^{2})^{2}-(x^{2}-y^{2})=0\,}$

• 

  Cassini curve : ${\displaystyle (x^{2}+y^{2})^{2}-(x^{2}-y^{2})+{\textbf {0,01}}=0}$

• 

  Szegö curve: ${\displaystyle x^{2}+y^{2}=e^{2\cdot x-2}}$

• 

  ${\displaystyle x^{2}+y^{2}+{\textbf {0,02}}=e^{2\cdot x-2}}$

• 

  Cartesian sheet : ${\displaystyle x^{3}+y^{3}=3\cdot x\cdot y}$

• 

  ${\displaystyle x^{3}+y^{3}+{\textbf {0,06}}=3\cdot x\cdot y}$

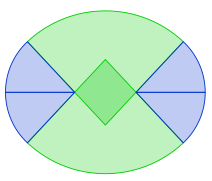
From circular arcs and straight lines

Ovals can also be composed of arcs and straight lines . However, such ovals have a lower smoothness than required in the definition above, since they are only in and not in . They are thus still smooth in the sense of a continuous derivative, but no longer have a continuous curvature. Instead, the curvature is constant on the subsections and has a point of discontinuity at the seams of the arcs or straight lines. ${\displaystyle C^{1}}$ ${\displaystyle C^{2}}$

Ovals composed of circular arcs and straight lines

literature

• AB Ivanov: Oval . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• Helmut Reckziegel, Markus Kriener, Knut Pawel: Elementary Differential Geometry with Maple . Vieweg + Teubner-Verlag 1998, ISBN 978-3-528-06991-9 , p. 43ff ( excerpt in the Google book search)
• Volkmar Wünsch: Differential Geometry: Curves and Surfaces . Vieweg + Teubner-Verlag 1997, ISBN 978-3-8154-2095-9 , p. 92ff ( excerpt from Google book search)
• John A. Adam: A Mathematical Nature Walk . Princeton University Press 2009, ISBN 978-0-691-12895-5 , pp. 124-136
• Charles Hutton: A Philosophical and Mathematical Dictionary . Volume 2, 1815, p. 141 ( full online version in Google Book Search - USA )
• Arnold Emch: Some Properties of Closed Convex Curves in a Plane . American Journal of Mathematics, Vol. 35, No. 4 (Oct. 1913), pp. 407-41 ( JSTOR 2370404 )
• N. Hansen Ball: On Ovals . The American Mathematical Monthly, Volume 37, No. 7 (Aug-Sep, 1930), pp. 348-353 ( JSTOR 2299271 )

Web links

Commons : Ovals  - collection of images, videos, and audio files

• Eric W. Weisstein : Oval . In: MathWorld (English).
• Norbert Harthun, Iris Rennert: The egg curve as a section of the hyperbolic cone (PDF; 158 kB)
• Egg curves at mathematische-basteleien.de (English)
• Paul L. Rosin: On the Construction of Ovals (English; PDF; 395 kB)
• André Heck: Mathematical Brooding over an Egg . In Loci , August 2008 - MAA online journal
• Egg Math - Collection of web-based teaching units for mathematics around the egg (English)

Individual evidence

1. ^ Heinrich Behnke: Fundamentals of Mathematics . MIT Press 1974, ISBN 978-0-262-02069-5 , p. 572 ( excerpt from Google book search)
2. ^ Oval in the Encyclopaedia of Mathematics (English)
3. ^ Helmut Reckziegel, Markus Kriener, Knut Pawel: Elementary Differential Geometry with Maple . Vieweg + Teubner Verlag 1998, ISBN 978-3-528-06991-9 , p. 43ff ( excerpt in the Google book search)
4. ↑ Volkmar Wünsch: Differential Geometry: Curves and Surfaces . Vieweg + Teubner Verlag 1997, ISBN 978-3-8154-2095-9 , p. 92ff ( excerpt in the Google book search)
5. ^ Catherine Cavagnaro, William T. Haight: Dictionary of Classical and Theoretical Mathematics . CRC Press 2001, ISBN 978-1-58488-050-9 , p. 88 ( excerpt from Google book search)
6. ^ Robert Clarke James, Glenn James: Math Dictionary . Springer 1992, ISBN 978-0-412-99041-0 , p. 300 ( excerpt from Google book search)
7. ^ Ian R. Porteous: Geometric Differentiation . Cambridge University Press 2001, ISBN 978-0-521-00264-6 , p. 36 ( excerpt in Google book search)