Conway's game of life
The game of life (English Conway's Game of Life ) is a game designed by mathematician John Horton Conway in 1970, based on a two-dimensional cellular automaton . It is a simple and still popular implementation of Stanisław Marcin Ulam's automata theory .
The playing field
The playing field is divided into rows and columns and ideally is infinitely large. Each grid square is a cellular automaton ( cell ) that can assume one of two states, which are often referred to as alive and dead . First, an initial generation of living cells is placed on the playing field. Each living or dead cell has exactly eight neighboring cells on this playing field, which are taken into account ( Moore neighborhood ). The next generation comes from following simple rules.
The game can be simulated manually on a piece of paper or with the help of a computer . Since a real playing field always has an edge, the behavior must be specified there. One can imagine the edge being occupied by dead cells, for example, so that some gliders change their direction of movement there. Another possibility is a torus- shaped playing field, in which everything that leaves the playing field at the bottom comes back in at the top and vice versa, and everything that leaves the playing field to the left re-enters the right and vice versa.
Alternatively, you can only simulate living cells and their direct environment and allocate more memory if necessary, since large dead areas remain dead. So at least one has a quasi-infinite field.
Instead of a square grid level, the simulation can also take place on a hexagonal grid level. Then the number of neighboring cells is not eight, but six. There are also three-dimensional Game of Life simulations.
Another possible variation is to introduce more than two possible states of the grid cells.
The rules of the game
The next generation is calculated for all cells simultaneously and replaces the current generation . The status of a cell ( alive or dead ) in the next generation depends only on the current status of the cell itself and the current status of its eight neighboring cells.
The rules Conway initially used are:
- A dead cell with exactly three living neighbors is reborn in the next generation.
|
|
- red: dead cell that will be born in the next generation
- green: living neighbors of the cell
- Living cells with fewer than two living neighbors die of loneliness in the next generation.
|
|
- A living cell with two or three living neighbors remains alive in the next generation.
|
|
- Living cells with more than three living neighbors die of overpopulation in the next generation.
|
|
- magenta: living cell that is viewed
- green: living neighbors of the cell
With these four simple rules, a variety of complex structures emerge from certain initial patterns in the course of the game. Some remain unchanged, others oscillate, and still others grow or fade. Some structures, so-called gliders , move on the playing field. Even logical functions like AND and OR can be simulated using certain initial patterns. This means that even complex functions of the circuit logic and digital computer technology can be reproduced.
There are other variants of the Game of Life in which Conway's rules are changed or supplemented. Examples are given in the section Deviating rules .
Points of view
Dealing with Game of Life can take place from different perspectives, such as:
- Behavior as a whole:
For some people it is interesting what kind of behavior certain sets of rules exhibit, for example whether they explode or implode , whether they slowly shrink or whether they slowly “harden”. - The biological aspect: Game of Life as a microcosm :
For others, Game of Life is like looking into a microscope. You observe the small structures that you can count and evaluate. Here you are particularly happy when a new "way of life" appears. Exploding, expanding or even “hardening” rule worlds are of no interest here. - The economic aspect: Game of Life as a model of computer trading in the financial markets :
According to the algorithms of computer trading, you buy a product when some, but not too many and not too few, neighbors already own it. If too few have it, you sell before it becomes worthless. If too many have it, sell before the bubble bursts. - The chemical aspect: energy and matter :
If you compare the frequency and the complexity of the game-of-life objects with the expenditure of energy and intermediate steps that are required to obtain a certain chemical compound , you can see the different life -Put objects on different energetic levels. Objects that appear in every sequence would then be at the level of water , carbon dioxide and sodium chloride . Objects such as balance wheel (2) and fountain would then, for example, be on the same level as hydrochloric acid and caustic soda , and objects such as sailors (LWSS, MWSS and HWSS) , which can also arise by chance, would already be on the level of relatively complex connections. - The physical aspect: Forces and initial value problem :
Even the simplest physical laws can show arbitrarily complex behavior as a whole. Purely deterministically / mechanically , any small deviations in the start condition can lead to very different results. Thus, an initial value problem can be formulated, followed by chaotic behavior. This is followed by final states, vibrations , growth, but also permanently irregular behavior. -
Game of Life as a machine :
There is the type of game-of-life interested person who is mainly interested in the construction of machines, i.e. structures that work like a machine or factory . There is a cluster of structures, from resemblance to a runway of an airport has to constantly start on the aircraft, and between them, drive the vehicles that maintain operations at their stations. - Game of Life as a computer model: It is possible to model a universal Turing machine and its input using complex start patterns . Conway's Game of Life is Turing-complete . In theory, any algorithmic problem that can be solved with a computer can also be calculated using Game of Life alone .
-
Game of Life in Theoretical Computer Science as a decision problem :
One can show that there is no algorithm that receives any two Game of Life configurations as input and can decide in all cases whether one configuration can arise from the other or not . This question is therefore undecidable.
The objects
With each generation step, a variety of complex structures emerges on the playing field. Some typical objects can be divided into classes based on any special properties they may have: they disappear, remain unchanged, change periodically (oscillate), move on the playing field, grow incessantly, etc.
Static objects
Static objects form a class of objects that no longer change in the course of the game without external influences, ie represent "stable cell systems".
Examples of static objects:
|
|
Oscillating objects
These are objects that change periodically according to a certain scheme, ie they return to the initial state after a finite, fixed number of generations.
The simplest cyclic configuration is a horizontal or vertical row of three living cells. In the horizontal case, a living cell is born directly above and below the cell in the middle, while the two outer cells die; so you get a vertical row of three.
A row of ten horizontally or vertically connected cells even develops into an object that has a cycle of fifteen generations, the pulsator .
Examples of oscillating objects are:
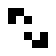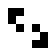 |
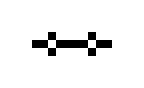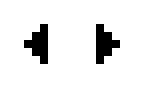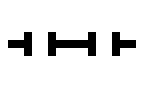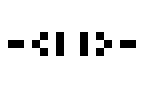 |
 |

|
|||||
| Surname | indicator | Clock | toad | Bipole | Tripole | Pulsator | porpoise | octagon |
| Cycles | 2 | 2 | 2 | 2 | 2 | 15th | 14th | 5 |
The pulsator is called the pentadecathlon due to a cycle of 15 steps and is a glider eater. The bottlenose dolphin , also known as the stand-up male , is called a tumbler in English .
Spaceships and gliders
Spaceships are (mostly oscillating) objects that follow a fixed direction. They are an example of the emergence appearances of the game of life; the few rules of the game say nothing about shapes that move infinitely, and yet the spaceships are created because of these rules. One can differentiate between the diagonal spaceships (for example gliders and jellyfish) and the vertical or horizontal spaceships (for example sailors).
Examples of spaceships are:
| Glider |
|
| Segler (1) (LWSS) ( L ight- W eight S pace s hip) |
|
| Segler (2) (MWSS) ( M iddle- W eight S pace s hip) |
|
| Segler (3) (HWSS) ( H eavy- W eight S pace s hip) |
|
The hacker emblem after Eric Steven Raymond is derived from the glider.
buffer
The buffers can be counted among the spaceships, whereby the buffers, in contrast to the spaceships, leave a trace of objects. These objects may well be other complex objects such as gliders or sailors.
Other objects
In addition, there are initial configurations that create an empty playing field within a finite number of time steps.
Another possibility is completely chaotic or exploding patterns. Despite its simplicity, the f- pentomino (also called r-pentomino) causes growth that appears chaotic for 1102 generations until the playing field forms an oscillating structure from the 1103rd step on. (Except for a few flying gliders. The example shows a limited field where everything outside is always dead.)
Another such object is the number 42 (with each digit on 3 by 5 boxes), which after 350 steps produces some static and some oscillating objects as well as 6 gliders.
Development from a random initial condition
The following animation shows the first 1500 development steps on a 100 × 100 toroidal playing field. The initial configuration is random with 31.25% live cells. Each state is displayed for 0.1 seconds. Each pixel stands for exactly one cell.
Conway's challenge
Conway offered $ 50 to anyone who could demonstrate that there is unlimited growth possible with Conway's Game of Life . Since orderly growth is necessary for unambiguous evidence, the chaotic explosive reproductions were unsuitable.
The first solution to this problem - a so-called glider cannon , which produces a glider at regular intervals - was presented in 1970 by the American mathematician Bill Gosper . The glider creates a shifted copy of itself within four generations , and so the cannon can create the next glider in the same place.
It is possible to create a glider cannon from collisions of gliders. This allows the direction of movement of the slider to be changed, and it is theoretically possible to construct self-replicating automata.
In the upper half of the picture is the glider cannon, which pulsates once every 30 generations, creating a glider. In the lower right part of the picture is the glider eater, which pulsates once in 15 generations and destroys a glider with every second pulsation. The sliders move from the center of the picture to the bottom right. The generation counter is running at the bottom left. The image description contains links to the GW- BASIC program generating the animation and to the start data .
In the meantime, an unmanageable number of constellations have been found that, like the simple glider cannon, continuously produce cells. In addition to gliders and various sailors, complex cannons have even been found that “fire” glider cannons themselves. Together with other useful structures, such as moving cannons, glider reflectors or relays (structures that, for example, brake gliders for a few generations), they form tools for the design of complex automata such as the Turing machine . This proves that Conway's Game of Life is Turing complete .
In 2012, a constellation was presented for the first time that is able to simulate a playing field that conformed to the rules of Conway's Game of Life (self-simulation).
Different rules
One can imagine different rules to the classic Game of Life . For example, the following set of rules defines a reproducing system, a "world of copying".
- Death rule: A cell with exactly 0, 2, 4, 6 or 8 living neighbors dies (or remains dead).
- Rule of Birth: 1, 3, 5 or 7 living neighbors create (or maintain) a living cell.
These rules can also be summarized as “number modulo 2”.
In this world of copying, for example, if you draw a structure in the form of the letter H, identical H-letters are created. In the case of larger initial samples, this set of rules even automatically moves the previously colliding copies apart. The copies of the output patterns occur with cycle numbers that are a multiple of 4. In the case of larger initial patterns, however, they do not occur with every multiple of 4. If you apply this rule to a field of size 15 × 15, all cells will always die out after the 15th generation.
In order to save yourself a cumbersome description of the rules when comparing different sets of rules, there is an abbreviated form for the rules of Game of Life: First (in ascending order) the digits of the number of neighbors in which a cell survives are placed next to one another, and then, separated by a slash , the digits that correspond to the values at which a cell is born. The classic Conway world is described by 23/3, the copier world described above by 1357/1357. Rules for multi-dimensional spaces have also been developed. Of course, display problems arise here. The rules 34/3 and 35/3 come very close to the behavior according to the classic 23/3 set of rules from Conway (two or three neighbors get a cell, three neighbors create a new cell). The number of all possible sets of rules results from the number of possibilities to select digits between 0 and 8 before and after the slash. Overall, therefore, sets of rules are conceivable, but most of them have only a few, trivial properties. Some of the more interesting regulations are described below.
The 3/3 world
So far, only one static object is known for this set of rules, which is not composed of other static objects. This object is the 2 × 2 block, which is also static in the 23/3 set of rules:
|
|
| Quadro |
Since every cell of this block has exactly 3 neighbors, it is trivially a static 3/3 object. The two-neighbors rule of Conway's classic 23/3 set of rules does not play a role for the block.
In the 3/3 world, for example, there are these oscillating objects:

|
||||||
| pedal | cone | Balance wheel (1) | swirl |
With the exception of the balance wheel (1), these objects are static under all possible sets of rules up to 345678/3, especially with the 34/3 and 35/3 rules discussed below. Balance (1) works under all sets of rules that contain 3/3 and 0/0124 does not (thus also in the Conway world, the 23/3 set of rules). Such objects can be called wanderers.
Most of the other objects cannot survive in the 3/3 world, however, so that the playing field is usually completely emptied within a few generations except for a few parts if the starting conditions are random.
The 13/3 world
This is a rule world with a few oscillating objects.
At least the following three oscillating objects are known:
 |
|
| ping-pong | O1G3 (2) (second oscillating object in the 1G3 world, also writable as O13-3 (2)) |
|
Pseudo-glider |
The 135/35 rule world can be viewed as a variant of the 13/3 rule world.
The 34/3 world
Oscillating objects of the 34/3 world:
 |

|
|||||||||||||||
| Strange | frog | O4G3 (3) | O4G3 (4) | pedal | cone | Balance wheel (1) | swirl |
While the 34/3 set of rules is important for Strange and Frosch, the pedal, pin, balance wheel (1) and vortex are also oscillating in the 3/3 world.
The 35/3 world
For example, in the 35/3 world there are these three moving objects:

|
| Float (1) and float (2) |

|
| 35/3 sailor |
As in the 34/3 rule world, the oscillating objects pedal, pin, balance wheel (1) and vortex occur in the 35/3 rule world.
The 2/3 world
This rule world should actually have belonged in the first place, because it contains an important oscillating object that is actually assigned to the 23/3 world, i.e. Conways Life, to which it is compatible:
|
|
||
| O2-3 (1) | Balance wheel (2) |
This means that there are at least three oscillating objects, including the balance wheel (1), which are incorrectly assigned to Conway's Game of Life (23/3) exclusively .
The 24/3 world
static objects:
|
|
oscillating objects:
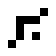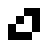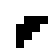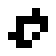
|
||||||||
| O24-3 (1) | O24-3 (3) | Sea cucumber | O24-3 (4) |
The 245/3 world
In addition to the oscillating objects that also appear in the 24/3 rule world, there are also a few other oscillating objects:
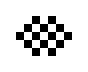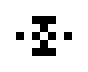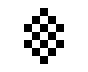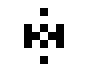 |
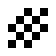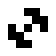
|
| O245-3 (1) | O245-3 (2) |
What is special, however, is the occurrence of a moving 7-cycle object, which in its type of movement resembles a jellyfish:

|
| jellyfish |
The 125/36 world
These two oscillating structures exist in the 125/36 rule world:
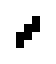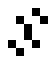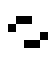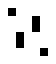 |
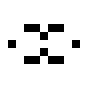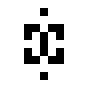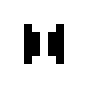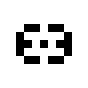
|
| O125-36 (1) | O125-36 (2) |
Anti-worlds
For every rule world there is an anti-rule world in the form that everything is inverted. So all cells that are otherwise dead are alive and all cells that are otherwise alive are dead. This is shown in the process by a black field on which the structures are white.
In order to create such an anti-rule world, the rules can be represented in the form of a switch field:
| 0 | 1 | 2 | 3 | 4th | 5 | 6th | 7th | 8th | |
|---|---|---|---|---|---|---|---|---|---|
| G | |||||||||
| T |
- G stands for birth.
- T stands for death.
The following assignment means that with three neighbors a dead cell becomes alive and a living cell dies with none or one as well as four to eight neighbors and otherwise the state of a cell remains untouched:
| 0 | 1 | 2 | 3 | 4th | 5 | 6th | 7th | 8th | |
|---|---|---|---|---|---|---|---|---|---|
| G | |||||||||
| T |
If the states of the switch field are rotated by 180 ° (not mirrored or tilted), the anti-rules are obtained:
| 0 | 1 | 2 | 3 | 4th | 5 | 6th | 7th | 8th | |
|---|---|---|---|---|---|---|---|---|---|
| G | |||||||||
| T |
Alternative rule name
| Rule name | comment | |
|---|---|---|
| 3/3 | G3 | |
| 13/3 | 1G3 | |
| 23/3 | 2G3 | Conway's original Game of Life |
| 34/3 | 4G3 | |
| 35/3 | 5G3 | |
| 236/3 | 26G3 | exploding, partly with the structures from 23/3 |
| 135/35 | 1G35 | extended 13/3 |
| 12345/3 | 1245G3 | a world in which a spreading, labyrinthine pattern is created |
| 1357/1357 | G1357 | a copying system whereby complex patterns can develop from simple, small structures |
| 24/35 | - | |
| 0123/01234 | - | a flashing world of spots |
| Anti-rules | comment | |
|---|---|---|
| 01234678/0123478 | 6G0123478 | Anti-Conway |
| 01234678/0123678 | 4G0123678 | Anti-4G3 |
| 02468/02468 | G02468 | Anti-copy system |
Consistent rule worlds
Game of Life simulations are conceivable in which delimited areas (e.g. left and right side) are each subjected to a different set of rules. One could track down moving hikers who can exist in both worlds of rules.
Web links
- Extensive wiki about Conway's Game of Life
- Detailed object catalog (static, oscillating, moving)
- The game of life simulates the game of life, video
- Game of life three-dimensional (2015), video
- Game of Life Universal Turing Machine, video
Simulations
- Video: Conway's Game of Life on an Intel 8008 computer (K1510) by ROBOTRON (1kByte code, 1kByte RAM) programmed in 1980. Recorded in the ROBOTRON Computer Museum.
- An implementation of Conway's Game of Life in JavaScript
- NetLogo contains the simulation Life in the "Models Library" supplied.
Java applications
- www.denkoffen.de/Games/SpieldesLebens/ (applet)
- www.ibiblio.org/lifepatterns (applet)
- www.hexatron.com/hexca (hexagonal) (applet)
- www.gridlife.info (download)
Implemented in Brainfuck
Individual evidence
- ↑ Conway's game of life (in html 5) on Math Fail
- ^ Paul Rendell: A Turing Machine in Conway's Game of Life, extendable to a Universal Turing Machine. Retrieved January 9, 2011 .
- ↑ Turtles, all the way down. Or gliders. Or glider turtles. Blog post about self simulation with video
- ↑ otcametapixel.blogspot.de
- ^ Uri Wilensky .: NetLogo Models Library: Cellular Automata / Life. Retrieved November 27, 2018 .










