Satellite orbit
A satellite orbit ( Latin orbis “circular path”, “circular motion”, from this orbita “ track ”) is the orbit of a satellite around a central body (sun, planet, moon, etc.). This article looks at satellites in orbit and their altitude. For a precise description of the trajectory, additional parameters are required, which are explained in the articles Orbital Elements and Satellite Orbital Elements .
Most space flights take place in low orbits (altitude a few 100 km, orbital times around 90 minutes) around the earth (e.g. space shuttle missions). The orbits of many navigation satellites are at medium altitude (23,000 km, 12 h orbital time) . The geostationary orbit at an altitude of 35,800 km (23h, 56min, 4.09s orbit) with an orbit inclination of 0 ° is also of particular importance . Seen from Earth, satellites in this orbit appear to be fixed over a point on the equator . This is particularly advantageous for communication and television satellites , since the antennas only have to be fixed once and then no longer have to be tracked. Due to the position above the equator, however, use in the polar regions is severely restricted or not possible at all.
Opposing demands are made on earth observation satellites or spy satellites . If possible, these should be able to observe locations on the entire surface of the earth, each for 10–15 minutes. In near-Earth space, this only works in orbits close to the polar , whereby here the sun-synchronous orbit (SSE) is more advantageous than the direct pole-to-pole orbit. With the SSE orbits, the constant sun angle in the observation area facilitates the evaluation and classification of the earth observation data obtained. The relatively low orbit also makes it easier to take detailed images. Especially in low orbits, the satellite orbit elements are subject to rapid changes due to the flattening of the earth .
species
Orbits off the equator
If an orbit does not run exactly over the equator (as with geosynchronous orbits, see below), in the simplest case it forms a circle, the center of which coincides with the center of the earth. (The following consideration also applies to elliptical orbits that are not too eccentric.) As a first approximation (without relativistic effects and external disturbances ) this orbital plane is fixed in space, while the earth rotates below it with its daily rotation. In this way, the satellite's “ ground track ” runs in a characteristic wave path around the earth, which shifts from revolution to revolution. In orbits close to the surface (also LEO, see below) the orbital time is about 100 minutes, so that the orbit (best readable at the two intersections of the orbit ellipse with the equatorial plane) shifts from one revolution to another by around 25 ° in a westerly direction (the earth has continued to turn to the east below). The resulting wave pattern with the parallel shifted circulation ground tracks can be seen in the figure. In the case of a circular path, this pattern is always symmetrical to the equatorial line.
The steeper the orbit is inclined towards the equator, the higher latitudes towards the poles are reached in the extreme points.
Park lane
Height: 150 to 200 km, possibly also elliptical orbits that reach higher or lower.
As a rule, a parking path represents a circular path that can be reached with little need for propulsion and which most of the launch vehicles initially control during the launch of a space probe. From here, the rocket can often more easily launch into the plane of the escape path. After measuring the inaccuracies that occurred when climbing into the parking lane, the ignition in the direction of the destination is calculated. The rocket then leaves the unstable parking lane again at the calculated point, often during the first orbit. Several types of rocket also use parking or intermediate orbits when launching satellites into higher orbits of the earth.
Low Earth Orbit (LEO)
(Low Earth Orbit, Near Earth Orbit)
- Altitude: 200 to 2000 km
- Altitudes between 1200 and 3000 km are theoretically conceivable, but are avoided if possible due to the high radiation exposure from the Van Allen Belt .
- LEO railways are the least energetic and are therefore the easiest to reach. Spacecraft move there at about 7 km / s. They need about 100 minutes to go around the earth. The visibility and radio contact with a ground station shall not exceed 15 minutes per round.
- Used for:
- Manned space travel (e.g. International Space Station ISS ; except for the Apollo missions , which only swiveled into a park orbit before their mission to the moon )
- Spy satellites (e.g. American keyhole satellites)
- astronomical satellites (e.g. the Hubble telescope )
- Earth exploration and weather satellites
- Amateur radio satellites
- Global communications satellite systems (such as Iridium )
- Research and technology test satellites ( e.g. TUBSAT-N and TET (satellite) )
Sun synchronous orbit (SSO)
In the sun-synchronous orbit, the satellite passes a point on the surface of the soil at the same true local time (± 12 hours local time ascending node , Eng. Local Time of Ascending Node , LTAN ). It is easier to compare observations on different days, since the shadows and the reflection behavior of surfaces do not change if the angle of incidence of the sun's rays is the same.
Medium Earth Orbit (MEO)
(Middle Earth Orbit)
- Altitude: 2,000 to below 36,000 km
- Special features: track height between LEO and GEO
- Used for:
- Global communication satellite systems such as Globalstar
- Navigation satellites such as GPS , Galileo or GLONASS
Polar orbit
Polar orbits run over the polar regions , i.e. the orbital inclination is close to 90 °.
Geotransfer Orbit (GTO)
- Altitude: 200-800 km perigee , 36,000 km apogee
- Special features: transition orbit to achieve a GEO (see also Hohmann transfer ). In most cases, the perigee is raised by the satellite itself by igniting a rocket motor during apogee.
Geosynchronous Orbit (GSO, IGSO)
An orbit with an orbit of 23h56min04s whose orbit is not necessarily circular or in the equatorial plane. If it is tilted , it is called an inclined geosynchronous orbit (IGSO), and if it is also highly elliptical, it is called a tundra orbit . The satellite remains at an average constant geographical longitude, but its geographical latitude fluctuates strongly over the day, or more precisely, it performs a sinusoidal oscillation around the equator in one day. Due to orbital disturbances caused by the uneven mass distribution of the earth, geostationary satellites are converted into an IGSO if no orbit corrections are made.
Geostationary Orbit (GEO)
- Altitude: 35,786 km
The orbit of a geostationary satellite always lies above the earth's equator. The orbit inclination to the equator is 0 degrees. In the case of orbital inclinations greater than zero, the satellite would apparently oscillate by the amount of the inclination perpendicular to the celestial equator , so that a true stationary orbit is only possible over the equator.
- Used for:
The acronym GEO derives from English G eostationary E arth O rbit from.
Some rockets such as the Russian Proton , the US Atlas V , Delta IV and Falcon Heavy as well as the European Ariane 5 are able to deploy satellites directly in geostationary orbit.
Super synchronous orbit
- Altitude: Greater than GEO orbit
A satellite in a supersynchronous orbit orbits the earth slower than it rotates with an apogee higher than 35,786 km. In the case of a high bullet inclination, it may be cheaper to first place a geostationary satellite on a supersynchronous transfer orbit (SSTO) instead of a GTO orbit.
Highly Elliptical Orbit (HEO)
Highly elliptical orbit satellites (HEO, "satellite with highly elliptical orbit") move on elliptical orbits with great eccentricity, that is, a large ratio of perigee and apogee . Typical values are 200 to 15,000 km or 50,000 to 400,000 km. Highly elliptical Earth orbits are suitable for research, telecommunications and military applications. Examples are:
- Very elliptical orbits for space telescopes that are supposed to stay over the Van Allen radiation belts for a very long time per orbit ( Integral , EXOSAT or IBEX ).
- Transfer orbit for spacecraft going to the moon.
- Transfer orbit for spacecraft flying to L1 or L2 .
- Molnija orbits : These are HEO with an inclination of 63.4 ° (arctan 2) and an orbital time of about 12 hours. The inclination, orbital time, perigee and apogee for satellites of the Russian Molnija series are: 63.4 °, 718 min, 450–600 km, 40,000 km (apogee over the northern hemisphere). With this inclination, the perigee rotation of the orbit caused by the earth's equatorial bulge disappears , so that the desired position of the apogee is maintained over a longer period of time. Satellites on Molnija orbits are ideally suited for supplying polar regions. Geostationary satellites are poor due to the low elevation in these areas and cannot be received at all above 82 °. A satellite with an orbital time of 24 hours stands in the earth's shadow for 2 to 4 hours, three satellites are required for all-day coverage.
Cemetery orbit
With graveyard orbit orbits are called, be maneuvered on the satellites after the end of its life.
- z. B. the orbit about 300 km above the GEO orbits
Other orbits
Very rarely do satellites use orbits that cannot be classified in this scheme. For example, the Vela ran to track down nuclear weapons tests above ground on only slightly elliptical, very high orbits between about 101,000 and 112,000 km altitude. That is too high for a MEO orbit and not enough elliptical for a HEO orbit.
The so-called Schuler period of 84.4 minutes is of theoretical interest . It is the shortest possible orbital time of a satellite if it were to orbit the earth at an orbit height of zero meters - if there were neither mountains nor air resistance.
Simplified overview of the orbits
| orbit | GEO | MEO | LEO | Molniya orbits |
|---|---|---|---|---|
| Altitude in km: | ≈ 36,000 | 6,000-12,000 | 200-1,500 | approx. 400-40,000 |
| Circulation time in hours: | 24 | 5-12 | 1.5-5 | 12 |
| Reception window for radio (with optimal geographical location of the ground station): | always | 2-4 hours | under 15 minutes | 8 hours |
| number of communication satellites required for global coverage: | 3 (polar regions only up to max. 82 ° latitude ) | 10-12 | 50-70 | 6, 3 each for the northern and southern hemispheres |
Orbital time
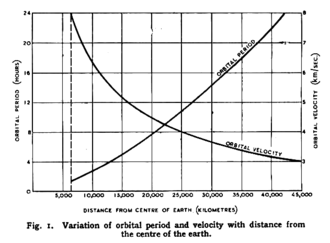
The orbital time and the equivalent orbital velocity in an orbit around a central body are determined by Kepler's laws and can be derived from
- (1)
- (2)
be calculated. Designate here
- the cycle time,
- the equivalent orbital velocity of a circular orbit,
- the great semi-axis ,
- and the masses of the central body and the satellite,
- the gravitational constant .
It should be noted that the revolution time is independent of the eccentricity and thus of the minor semi-axis of the path. All elliptical orbits in the same system with the same major semi-axis require the same orbital time.
With an assumed earth radius of 6371 km, an earth mass 5.974 · 10 24 kg and the gravitational constant 6.6742 · 10 −11 m 3 kg −1 s −2 , as well as a satellite mass that is negligible compared to the earth mass, the orbital time can be calculated from the orbit height h above the Earth surface can be calculated as follows:
- (1a)
If the satellite mass is neglected, the calculation of the orbital velocity is simplified (for calculation, see orbits near the surface ):
- (2a)
With
Starting place
For equatorial or equatorial orbits such as geostationary orbits, a starting location near the equator is advantageous. Relatively little fuel is then required for the orbit correction maneuvers that bring the satellite into the desired orbit. In addition, a starting point close to the equator has the advantage that the payload already receives a relatively high horizontal speed from the earth's rotation . In particular, Ariane, with its launch site in the Guiana space center , has an advantage here, as does Sea Launch with its lake platform near the equator.
lifespan
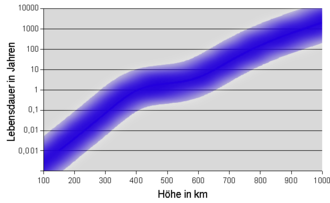
Low-flying satellites only stay briefly in their orbit around the earth. The friction with the atmosphere slows them down and lets them crash to the earth. At an altitude of 200 km, they only stay in orbit for a few days. For this reason, low-flying spy satellites fly on highly elliptical orbits. They only burn up when the apogee has also decreased to about 200 km.
The International Space Station orbits the earth at a distance of approx. 400 km and loses 50 to 150 m height per day. Without reboosts, it would burn up in a few years. From an altitude of 800 km, satellites remain in space for more than 10 years, high-flying satellites practically forever. When decommissioned, they contribute significantly to space debris. The diagram illustrates the dwell times. The higher the solar activity, the further the atmosphere expands and the greater its influence on higher orbits. The kink in the curve illustrates the reduced solar activity every 11 years.
The satellite geometry also influences the friction. The lower the mass and the greater the flow cross-section and the speed relative to the atmosphere ( ballistic coefficient ), the greater the friction, thus the decrease in speed and thus the decrease in the orbit height. During the flight through the earth's shadow, the International Space Station aligns its rotating solar panels in such a way that the average resistance is reduced by 30% (so-called Night Glider mode ).

A prediction about the crash location of a satellite on earth is practically impossible. As an example, the picture shows the low-flying satellite ROSAT , which crashed in October 2011. During a 5-hour observation, the satellite covered the distance marked as a red ground trace. The impact zone for the various debris always forms an elongated ellipse in the direction of the track. In order to limit the impact location to a continent, the forecast for a satellite crash would have to be accurate to 15 minutes. Even a few days before it finally burns up, orbit disturbances and the interactions with the atmosphere are too great to sensibly limit the time of impact. The inclination of the satellite orbit determines which latitudes are not flown over and are outside the risk zone. For a polar satellite with an inclination of almost 90 ° it is the entire surface of the earth, for a ROSAT with an inclination of 53 ° it is the area between 53 ° north and 53 ° south.
Visibility with the naked eye
Satellites and other low-orbit objects are typically made of metal so that they reflect light well. If they are illuminated by the sun, enough light is reflected so that they can also be seen with the naked eye. To do this, however, several conditions must be met: it must already be dark enough on the ground so that the light reflex can stand out from the sky background; however, the satellite must still be fully illuminated by the sun. These two conditions are only given immediately after sunset or directly before sunrise when it is night on the ground, but the sun is above the horizon at the height of the satellite as seen from it. The third condition is that at this point in time the satellite must also cross the observer's field of view, which, as explained above, is not too large. Thus, a satellite only reaches a certain region away from the equator at larger time intervals at the appropriate times mentioned, see the discussions at the ISS as an example . The fourth condition is simply that the clouds must not obstruct the view.
For the observer, the problem arises of distinguishing such satellite reflections from aircraft. Satellites appear considerably faster and more uniform in their movement, they are typically only a few minutes in the field of view. In addition, they don't have flashing lights like normal aircraft.
For the ISS and many other satellites there are websites with dates for upcoming sightings.
A special feature are the so-called Iridium flares , which arise when the satellites of the Iridium satellite telephone system reflect the sun precisely towards the observer for a moment. The effect is exceptionally strong because these satellites have a very large, flat, reflective surface. Due to the decommissioning of older Iridium satellites, the flares will rarely occur and will probably be a thing of the past by the mid-2040s.
literature
- Oliver Montenbruck u. a .: Satellite orbits - models, methods, and applications. Springer, Berlin 2001. ISBN 3-540-67280-X
- Byron D. Tapley et al. a .: Statistical orbit determination. Elsevier Acad. Press, London 2004. ISBN 0-12-683630-2
- Guochang Xu: Orbits. Springer, Berlin 2008. ISBN 3-540-78521-3
- FO Vonbun u. a .: Orbit determination accuracies using satellite-to-satellite tracking. in: IEEE Transactions on Aerospace and Electronic Systems. Vol. AES-14, Ed. Nov. New York 1978, pp. 834-842. bibcode : 1978ITAES..14..834V
Web links
- Bernd Leitenberger: Orbits
- AMSAT: Software for satellite observation (English)
- Andreas Grieß (Statista) / che: Infographic on satellites: China surpasses Russia in orbit , in Spiegel Online
Individual evidence
- ^ Bruno Stanek: Raumfahrt Lexikon , Halwag Verlag, Bern, page 221, 1983, ISBN 3-444-10288-7
- ↑ What's So Special About Low Earth Orbit? wired.com, accessed February 15, 2016
- ↑ Hans-Martin Fischer: European news satellites from Intelsat to TV-Sat . Stedinger Verlag, Lemwerder 2006. ISBN 3-927697-44-3
- ↑ Heavens-Above - worldwide observation possibilities of the ISS, Iridium Flares and other satellites
- ↑ Calsky - Comprehensive site for calculating the orbit of satellites (with star map)
- ↑ Satellite Sighting Information - times and locations of the ISS and shuttles in the night sky over Germany
- ↑ The Iridium Flare Era is About to End. In: Universe Today. March 19, 2019, accessed July 30, 2019 .