Fallacy (mathematics)

There are mathematical fallacies and fallacies in many branches of mathematics . Optical illusions and fallacies are in the philosophy fallacies (collectively, English fallacy , Latin fallacia = deception), respectively. In mathematics , false evidence is evidence in which fallacias occur. Quite a few false conclusions have played a role in the history of mathematics and were the starting point for mathematical research. In mathematical didactics, uncovering false evidence is one of the problem-solving activities.

In the case of fallacies, the person who makes them acts in good faith, while in the case of fallacies, the intention to deceive is essential. This distinction is admittedly not sharp. Fallacies lead to a false result through a seemingly plausible list. The trick is to cover up the mistake in such a way that it is not noticeable at first and only becomes apparent when the result is absurd. Laypeople and beginners in particular may not immediately see where the error is. Fallacies can be presented as a mathematical joke in which typical mathematical inferences are applied in an absurd context.

In elementary algebra, typical examples include a step where division by zero occurs, a root is wrongly extracted, or more generally where different values ​​are equated to an ambiguous function. Well-known fallacies are also known in analysis and Euclidean geometry . Famous bogus evidence is based on divergent series from which almost any nonsense can be deduced.

Very little is known about the history of fallacies, with a few exceptions, such as the fallacy-based paradoxes of Zeno of Elea . In many cases, mathematical jokes are spread by word of mouth and only later published somewhere (usually without giving a name) without it being known whether this is really the first publication.

The following are

Fallacies and sham evidence

framed in a box as shown. A drop-down text field "Resolution [expand]" in the box explains the list if necessary.

arithmetic

Correct result despite wrong calculation

A separate class of fallacies ( English howler 'gross blunder' ) arise from a correct conclusion despite incorrect “derivation”. Sometimes two mistakes cancel each other out and get the right result. Such faulty arguments only lead to the correct result in special cases , so they have no general validity and are mathematically worthless.

So someone can check the price of a purchase of the goods listed in the table

amount	Would	Unit price	Unit of measure
¼ pf	butter	2 s 10 d	pf
2½ pf	lard	10 d	pf
3 pf	sugar	3¼ d	pf
6 boxes	matches	7 d	12 boxes
4 packages	Soap flakes	2½ d	package

1. ↑ ^{a b} pf = pound , s = shilling = 12 d (denarii, pennies)

Add up by simply adding up the individual prices to the - nevertheless - correct final price:

4 s 8¾ d	= 8½ d + 2 s 1 d + 9¾ d + 3½ d + 10 d
	= 2 s 10 d + 10 d + 3¼ d + 7 d + 2½ d

The " shortening " of digits and characters in a fraction only leaves the quotient unchanged in exceptional cases:

${\displaystyle {\frac {26}{65}}={\frac {26\!\!\!/}{6\!\!\!/5}}={\frac {2}{5}}}$ or more daring  ${\displaystyle {\frac {a^{2}-b^{2}}{a-b}}={\frac {a^{2\!\!\backslash }{-\!\!\!\!/}\;b^{2\!\!\backslash }}{a\!\!\!\backslash -\!\!\!\!\!/\;b\!\!\!\backslash }}=a+b}$

Extracting summands from a root

${\displaystyle {\sqrt {5+{\frac {5}{24}}}}=5{\sqrt {\frac {5}{24}}}\quad {\text{oder}}\quad {\sqrt {12+{\frac {12}{143}}}}=12{\sqrt {\frac {12}{143}}}}$

is normally not allowed, but is based on the general rule

${\displaystyle {\sqrt {n+{\frac {n}{n^{2}-1}}}}=n{\sqrt {\frac {n}{n^{2}-1}}}}$

Linking like with like

A physical quantity consists of a numerical value and a unit of measurement . If factors are hidden in intentions for the units of measurement but are not treated like factors, this can easily lead to fallacies, for example:

2 kg = 2000 g

3 kg = 3000 g

The same multiplied by the same results in the same, i.e.:

6 kg = 6,000,000 g = 6,000 kg.

resolution

If the units are also squared, the result is correct: (2 kg) · (3 kg) = 6 kg² = (2000 g) x (3000 g) = 6,000,000 g² = 6 x (1000 g) ² = 6 kg²

It is instructive here that the consideration of the units in an invoice provides a criterion for their verification. At the end of the calculation, the units on both sides of an equation and in all summands of a sum must match.

Throwing apples and pears together also leads to incorrect mathematical conclusions:

No cat has eight tails.

A cat has one more tail than no cat.

Adding the same to the same results in the same, i.e.:

A cat has nine tails.

resolution

The “no cat has” in the first sentence is short for “there is no cat to whom this statement applies”. This phrase is not synonymous with “If you count the tails of 0 cats, you get 8”. Here, different meanings of the word “none” are inadmissibly equated.

algebra

Division by 0

From the identity 0 · a = 0 · b, after division by the common factor 0 on the right and left side, the identity a = b follows, which does not always have to be correct. This illegal division is hidden in the following examples by introducing variables.

Sentence: 2 = 1

Proof:

1. It applies	: a = b
2. Multiplication by a	: a² = ab
3. Add a² - 2 off	: a² + (a² - 2 from) = from + (a² - 2 from)
4. Summarize	: 2 (a² - ab) = a² - ab
5. Eliminate a² - ab	: 2 = 1

Qed

resolution

In the fifth step, because a = b, it is divided by a² - ab = a (a - b) = 0.

The false evidence of 1 + 1 = 2 belongs to the category of “mathematical joke”. Here mathematicians make fun of the tendency to formulate a sentence as generally as possible in order to expand its applicability and then to include the reason for the investigation as a special case.

Sentence: 1 + 1 = 2

Proof:

1. Starting point	: n (2n - 2) = n (2n - 2)
2. Summarize	: (n - n) (2n - 2) = 0
3. Simplify	: 2n - 2 = 0
4. Change over	: 2n = 2
5. Forming	: n + n = 2

With n = 1 it follows that Qed

resolution

The third step is dividing by n - n = 0.

To represent the equation 1 + 1 = 2 as a special case of the “generally valid” equation n + n = 2 is of course absurd.

Equating ambiguous expressions

A non-zero square number always has two different roots, a positive and a negative. By equating both, amazing fallacies can be "deduced" according to the scheme (-a) ² = (+ a) ² → -a = a.

Theorem: All numbers are the same

Proof sketch: If any two numbers a and b are always the same, then all numbers are the same.

1. Starting point:	: a + b = t with any a and b
2. Multiply by (a - b)	: (a - b) (a + b) = (a - b) t
3. Multiply out	: a² - b² = at - bt
4. Change over	: a² - at = b² - bt
5. Add t² / 4	: a² - at + t² / 4 = b² - bt + t² / 4
6. Second binomial formula	: (a - t / 2) ² = (b - t / 2) ²
7. Simplify	: a - t / 2 = b - t / 2
8. Add t / 2	: a = b

Qed

resolution

In the seventh step, the two different roots of a square are equated. With a - t / 2 = - (b - t / 2) ↔ a + b = t the fallacy would have been avoided.

In the realm of complex numbers , every number has two different square roots (other than zero). In the expression , the expression on the right-hand side stands for two values ​​+ i and -i, while on the left there is a fixed complex number. This can give rise to false conclusions. ${\displaystyle {\rm {i={\sqrt {-1}}}}}$

1. Starting point	:  ${\displaystyle {\frac {-1}{1}}={\frac {1}{-1}}}$
2. Root extraction	:  ${\displaystyle {\frac {\sqrt {-1}}{1}}={\frac {1}{\sqrt {-1}}}}$
3. Insertion of i	:  ${\displaystyle {\rm {i={\frac {1}{i}}}}}$
4. Multiply by i	:  ${\displaystyle {\rm {i^{2}=1}}}$
5. Insert i² = -1	:  ${\displaystyle -1=1}$

resolution

In the third step, the positive and negative roots of -1 are set equal. If this is not done, the contradiction is avoided: ${\displaystyle {\rm {i={\frac {1}{-i}}\quad \rightarrow \quad i^{2}={\frac {1}{-1}}=-1}}}$ The power law (w / z) r = w r / z r is only valid to a limited extent in the complex.

The following chain of equations also makes use of this fact:

${\displaystyle -1={\rm {i\cdot i={\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {(-1)(-1)}}={\sqrt {1}}=1}}}$

resolution

In the case of the middle equal sign , the usual positive main value of the root in the real is used on the right-hand side. Here, however, only the negative value leads to the correct result ${\displaystyle {\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {(-1)(-1)}}}$ ${\displaystyle -1={\rm {i\cdot i={\sqrt {-1}}\cdot {\sqrt {-1}}=-{\sqrt {(-1)(-1)}}=-{\sqrt {1}}=-1}}}$. The power law (w z) r = w r z r is only valid to a limited extent in the complex.

It is not more correct if i appears in the exponent.

1. Euler's relation with y = 2π	:  ${\displaystyle e^{2\pi {\rm {i}}}=1}$
2. Raise to the i th power	:  ${\displaystyle \left(e^{2\pi {\rm {i}}}\right)^{\rm {i}}=1^{\rm {i}}}$
3. Simplify	:  ${\displaystyle e^{-2\pi }=0{,}001867\ldots =1}$

resolution

In the second step, there are ambiguous functions to the left and right of the equal sign whose value ranges and are the same. In the third step, two unequal elements - the main values ​​of the powers - are picked out of these value ranges and equated, which leads to the fallacy. ${\displaystyle \left\{z\in \mathbb {C} |z^{i}=\left(e^{2\pi {\rm {i}}}\right)^{\rm {i}}\right\}}$ ${\displaystyle \{z\in \mathbb {C} |z^{\rm {i}}=1^{\rm {i}}\}}$ The power law (z a ) b = z a · b is only valid to a limited extent in the complex.

Analysis

Differential calculus

In the differential calculus are differentials d x used, which are zero in certain cases, for example where x is a constant. As in algebra, fallacies can be constructed from this.

Theorem: There is no point on a circle that is closest to another point that is not on the circle and not at its center.

Proof of differential calculus.

1. A circle with radius b around the center point M is given.
2. Let P be the point to which the next point on the circle is sought.
3. The origin of a Cartesian coordinate system , the x-axis of which goes through the center M, is placed in the point P. The x-coordinate of M is a.
4. For a point R = (x, y) on the circle, according to the Pythagorean theorem : (x - a) ² + y² = b² or x² + y² - 2 ax + a² - b² = 0
5. According to Pythagoras, the square of the distance between P and R is r²: = x² + y².
6. This is used in (4.): r² - 2 ax + a² - b² = 0.
7. The distance PR is extremal when the derivative r '(x) = 0.
8. The derivation of (6.) with respect to x results in 2 rr '- 2 a = 0 or r' = a / r, because by assumption P does not lie on the circle and therefore r ≠ 0.
9. According to (8.), the condition r '= 0 is only fulfilled if a = 0, i.e. P = M.
10. For all points that are not on the circle but outside the center of the circle, there is no next point on the circle.

Qed

resolution

The points R = (x, y) on the circle, which are at an extreme distance from the origin of the coordinate system, lie on the x-axis with y = 0 and (x - a) ² = b². Calculating the differential of x leads to 2 (x - a) dx = 0. For a point on the circle and the x-axis, dx = 0 because of x - a │ = b ≠ 0. This makes it clear noticeable that the circle intersects the x-axis perpendicularly. The environment in the x-direction necessary for the differentiation with respect to x does not exist on the circle at these intersection points on the x-axis, r '(x) cannot be calculated in the extremum, and all statements inferred from r' = 0 are invalid. So the crucial mistake is made in the third step. This example emphasizes the rule that the independent variable, here x, in the extremes of the dependent variable, here r, must not be subject to any constraints. It doesn't get any better if the center point is not on the x-axis. The two-dimensional environment then required for the differentiation according to the two independent variables x and y is reduced to a one-dimensional arc. The problem can be solved by non-linear optimization , where instead of the objective function with constraints, a Lagrange function without constraints is considered. The condition that R lies on the circle is built into the objective function with a Lagrangian multiplier λ: f (x, y, λ) = x² + y² + λ (x² + y² - 2 ax + a² - b²) → stat. Derivation of the Lagrange function f with respect to y yields at stationarity 2 (1 + λ) y = 0 i.e. 1 + λ = 0 or y = 0. Derivation from f with respect to x shows with stationarity 2 (1 + λ) x - 2 λ a = 0, in both cases a = 0 or x = a λ / (1 + λ). The derivation from f to λ finally leads to x² + y² = b² for a = 0 or (x - a) ² - b² = 0 for y = 0, which is the correct solution. A parameterization of the plane with cylindrical coordinates (r, φ) so that (x, y) = (r cos φ, r sin φ) with r = r (φ), allows the extraction of the points closest to the origin, namely the angle In the extremum φ is not subject to any secondary conditions: r² - 2 ax + a² - b² = r² - 2 ar cos φ + a² - b² = 0 → 2 rr '- 2 ar' cos φ + 2 ar sin φ = 2 (r - a cos φ) r '+ 2 ar sin φ = 0 Now r '= 0 implies the identity ar sin φ = 0 and therefore a = 0 or sin φ = 0, as long as the circle does not go through P and thus r ≠ 0. So the points with extreme distance with φ = 0 ° or φ = 180 ° are found.

Integral calculus

In the derivation of a function f (x) to the variable x all fall independent of x terms - in particular constants - out. Conversely, the antiderivative - the indefinite integral - is only determined up to a constant of integration . Thus, according to the scheme f ₁ '(x) = f ₂ ' (x) → f ₁ (x) = f ₂ (x), which does not always have to be correct, fallacies can be constructed.

Sentence: 0 = 1

Proof of Partial Integration :

1. Starting point	:    with the natural logarithm ln. ${\displaystyle I=\int {\frac {1}{x\ln x}}\mathrm {d} x}$
2. Definition of the first factor	:  ${\displaystyle u=\ln x\quad \rightarrow \quad u'={\frac {1}{x}}}$
3. Definition of the second factor	:  ${\displaystyle v={\frac {1}{\ln x}}\quad \rightarrow \quad v'=-{\frac {1}{(\ln x)^{2}}}{\frac {1}{x}}=-{\frac {1}{x(\ln x)^{2}}}}$
4. Use of the functions	:  ${\displaystyle I=\int u'\cdot v\,\mathrm {d} x}$
5. Partial integration	:  ${\displaystyle I=u\cdot v-\int u\cdot v'\,\mathrm {d} x}$
6. Replace the functions	:  ${\displaystyle I=\ln x{\frac {1}{\ln x}}+\int \ln x\cdot {\frac {1}{x(\ln x)^{2}}}\,\mathrm {d} x}$
7. Simplify	:  ${\displaystyle I=1+\int {\frac {1}{x\ln x}}\,\mathrm {d} x}$
8. Insertion of I	:  ${\displaystyle I=1+I}$
9. Subtract from I.	: 0 = 1
Qed

resolution

In the fifth step, partial integration, the integration limits were generally removed for partial integration. Therefore, the constant of integration C must be observed there. Then in 8) I = 1 + I + C without contradiction. See also Partial Integration # Indefinite Integrals and Partial Integration , where a further fallacy can be seen in the subsection reciprocal function .

Derivations from divergent series

With divergent series (almost) everything can be "proven". A famous bogus evidence based on it is the following.

Theorem: The following applies to the sum C of the natural numbers : C = 1 + 2 + 3 +… = -1/12.

Proof by calculating.

The starting point is the infinite series

A = 1 - 1 + 1 - 1 + 1 - 1 + - ...

With the gradual addition of the terms of the sequence, the values ​​0 and 1 occur equally often for the row as when flipping a perfect coin and therefore ½ is the expected value of the row. Now is

A.	= 1 - 1 + 1 - 1 + 1 - 1 + - ...
	= 1 + (1 - 2) + (-2 + 3) + (3 - 4) + (-4 + 5) + (5 - 6) + ...
	= 1 + 1 - 2 - 2 + 3 + 3 - 4 - 4 + 5 + 5 - 6 - 6 + + - - ...
	= 2 (1 - 2 + 3 - 4 + 5 - 6 + - ...)
	= 2 * B

With

B: = 1 - 2 + 3 - 4 + 5 - 6 + - ...

This series is proportional to the searched series C, because

C - B	= 1 + 2 + 3 + 4 + 5 + 6 +… - (1 - 2 + 3 - 4 + 5 - 6 + -…)
	= (1 - 1) + (2 + 2) + (3 - 3) + (4 + 4) + (5 - 5) + (6 + 6) + ...
	= 0 + 4 + 0 + 8 + 0 + 12 + ...
	= 4 (1 + 2 + 3 + ...)
	= 4 * C

So 3 · C = -B or with B = A / 2 = ¼:

C = 1 + 2 + 3 +… = -B / 3 = -1/12

Qed

resolution

Almost everything is wrong in the derivation. To show this, the n -th partial sums, indicated by the index n , are first considered with an even n . Then ${\displaystyle A_{n}=(1-1)+\dots +(1-1)=0+\dots +0=0}$ and ${\displaystyle B_{n}=\underbrace {(1-2)+(3-4)+\dots +(n-1-n)} _{{\frac {n}{2}}\cdot (-1)}=-{\frac {n}{2}}}$ In sum ${\displaystyle {\begin{aligned}B_{n}+B_{n}=&\underbrace {1+(1-2)+(-2+3)+\dots +(n-1-n)} _{A_{n}}-n\\=&A_{n}-n\end{aligned}}}$ there is still a “remainder” n , which also results from the expressions for A n and B n . The formula B n = A n / 2 is therefore wrong in the first order of n . However, that is not enough to explain the second-order incorrect end result. The difference C n - B n of the partial sums gives: ${\displaystyle {\begin{aligned}C_{n}-B_{n}=&1+2+\dots +n-(1-2+-\dots -n)\\=&4\cdot \left(1+2+\dots +{\frac {n}{2}}\right)=4C_{n/2}\end{aligned}}}$ According to the empirical formula for C n , the ratio approaches ${\displaystyle {\frac {C_{n}}{C_{n/2}}}={\frac {{\frac {n}{2}}(n+1)}{{\frac {n}{4}}({\frac {n}{2}}+1)}}=4{\frac {n+1}{n+2}}}$ with increasing n of the four and because C n increases with the square of n , the formula C n = - B n / 3 is wrong in the second order. Only after this error does C no longer grow quadratically with n . Expressions of C n / 2 through C n confirmed ${\displaystyle C_{n}-B_{n}=4C_{n/2}={\frac {n+2}{n+1}}C_{n}\quad \rightarrow \quad C_{n}=-(n+1)B_{n}={\frac {n}{2}}(n+1)}$ If n is odd ${\displaystyle {\begin{aligned}A_{n}=&1\\B_{n}=&{\frac {n+1}{2}}\\C_{n}-B_{n}=&4C_{(n-1)/2}\end{aligned}}}$ with a similarly devastating result.

Row A can also be used to construct the following fallacy:

A.	= 1 - 1 + 1 - 1 + ...	= 1 + (-1 + 1) + (-1 + 1) + ...	= 1 + 0 + 0 +…	= 1
A.	= 1 - 1 + 1 - 1 + ...	= (1 - 1) + (1 - 1) + ...	= 0 + 0 +…	= 0
→ 1	= 0

resolution

The indefinite divergent series A n cannot be assigned a value for n → ∞. The comparison of two indefinite values ​​is mathematically pointless.

logic

Inadmissible inferences

Fallacies in propositional logic can result from the difference between the subjunction “→” and the bijunction “↔”: “If a then b” does not always mean “if b then a” for two statements a and b, as the following example shows .

Theorem: 3 = 0

Algebraic proof:

The starting point is the equation

x² + x + 1 = 0.

Since x ≠ 0 is obviously here, this is equivalent to

x ≠ 0 and x · 0 = x · (x² + x + 1) = x³ + x² + x = 0.

Adding 1 on both sides of this equation further yields:

x³ + x² + x + 1 = x³ + 0 = x³ = 1.

So x = 1 which implies 1² + 1 + 1 = 3 = 0 in the first equation.

Qed

resolution

In the area of real numbers , x² + x + 1 ≠ 0 and nothing more meaningful can be inferred from the wrong equation x² + x + 1 = 0, see paradoxes of material implication .

In the complex the polynomial p (x): = x² + x + 1 has two conjugate complex zeros x 1,2 = -½ ± i √ (¾), which are also the solution of x³ - 1 = 0. The cubic polynomial q (x): = x³ - 1 has three zeros in the complex - one more than p - two of which also result in p (x) = 0. The third and only real zero of q is one and accordingly it cannot be the zero of p. So in the complex is x² + x + 1 = 0 → x³ = 1 correct but the opposite statement x³ = 1 → x² + x + 1 = 0 wrong, as the counterexample x = 1 shows.

Complete induction

→ Main article : Horse paradox

The full induction is a mathematical proof method by which a statement for all natural numbers , it is proved that is greater than or equal to a certain initial value, for example 1, are. At the beginning of induction 1, the statement often applies. Then it is proven in the induction step that if the statement holds for n (induction assumption) it also holds for n + 1. It then applies to n = 1, hence also to n = 2, therefore also to n = 3, etc. If applied incorrectly, pseudo-proofs such as the following can arise.

Sentence: All Germans are the same age.

Proof of Complete Induction:

The assertion that in a group of n people from the population of all Germans are all of the same age is denoted by S (n).

Induction start

In a “group” of just one person, all people in the group are of the same age. The statement S (1) applies in any case.

Induction assumption

Let the claim S (n) be correct for n ≥ 1. In a group of n Germans, everyone is the same age.

Induction step

Here we have to prove that if S (n) is true, this also implies validity of S (n + 1). To do this, n + 1 Germans are placed in a row.

First of all, the first person P is taken from the line.

What remains in the row are n Germans who are of the same age according to the requirements. P is placed back at the first position in the row and the last person Q is removed from the row.

What remains are n Germans who are all of the same age according to the requirements. So all people in the series are of the same age and the claim S (n + 1) is true.

Induction closure

This proves S (n) for all n and all Germans have the same age.

resolution

The problem here is the step from n = 1 to n + 1 = 2. There is no person R who is among the last n and among the first n people at the same time. Thus, it cannot be concluded that because the first person P has the same age as R and the last person Q has the same age as R, the first and last person, P and Q, are also of the same age. This conclusion requires at least three people P, Q and R.

Lazy definitions

See also : well-definedness

The fallacies in the field of lazy definitions are based on the logical concept

All properties apply to the elements of the empty set.

In itself, this is a reasonable arrangement, since all sets are extensions of the empty set. However, a non-existent object can be misused for fallacies, because it has suitable properties for this.

For example, the greatest natural number .

Let be the greatest natural number, i.e. N ≥ n for all . In particular, this also applies to n: = N + 1 , which is why N + 1 = n ≤ N follows. On the other hand, N 1 and N - 1 0 , which is why and N - 1 N or N N + 1 holds. This means that N ≤ N + 1 ≤ N or 0 ≤ 1 ≤ 0, which only allows the conclusion 1 = 0. ${\displaystyle N\in \mathbb {N} _{0}}$ ${\displaystyle n\in \mathbb {N} _{0}}$ ${\displaystyle N-1\in \mathbb {N} _{0}}$

resolution

All conclusions are correct under the premise made. However, because this is contradictory - there is no greatest natural number - nothing can be said about the truth of the results found. Conversely, a proof for the non-existence of a greatest natural number can be made from the above derivation.

Another example shows that expanding a range of numbers should be done with care.

Let j be the “imaginary” number for which 0 · j = 1 applies.

Then 1 = 0 · j = (0 + 0) · j = 0 · j + 0 · j = 1 + 1 = 2

or 0 = 1.

Fallacies in geometry

In geometry, fallacies can be hidden behind inaccurately drawn sketches. The geometrical relationships shown in the sketches cannot appear on closer inspection. The believer is thus led to the fallacy. The following examples take advantage of this.

Fallacy of the equilateralism of all triangles

Theorem: All triangles are isosceles .

Proof after construction:

1. An arbitrary triangle ABC is given as in the picture.
2. Let m be the bisector of the interior angle in A.
3. The center perpendicular of side BC intersects this at point D and the bisector m at point O.
4. The triangles BDO and COD are congruent according to the second theorem of congruence, because the side lengths DO and BD or CD are the same and the interior angles in D match.
5. Therefore, BO = CO.
6. Let R be the base point of the perpendicular from O to the side (AB) and Q the base point of the perpendicular from O to the side (AC).
7. The triangles ARO and AOQ are congruent according to the SWW congruence theorem, because the hypotenuse AO, an adjacent angle in A and the opposite angle in R or Q coincide as right angles .
8. Therefore AR = AQ and OR = OQ.
9. The triangles BOR and CQO are congruent according to the fourth theorem of congruence, because according to (5.) and (8.) they coincide in two side lengths according to BO = CO and OR = OQ and in the angle opposite the longer side. Because according to (6.) the right angle in R or Q lies opposite the hypotenuse of the triangles BOR and CQO under consideration.
10. So BR = CQ.
11. According to (8.) and (10.), AB = AR + BR = AQ + CQ = AC.

Qed

resolution

The mistake here is that the point O in a non-isosceles triangle always lies outside the triangle on its circumference , namely in the middle of its arc above the side BC. According to construction, D, R and Q lie on the Simson straight line with the pole O. According to Pasch's axiom , Q and R cannot both lie on the triangle sides between the corners. In the triangle ABC of the drawing, the base point of the perpendicular from O on (AB) is not on the side (AB), but on the half-line [AB seen from A behind B. The identities (5.), (8.) and ( 10.) apply, but AB and BR are oppositely oriented. Therefore (11.) is correct AR = AB + BR = AQ = AC - CQ = AC - BR. This does not mean that triangle ABC is isosceles.

The fallacy of the empty circle

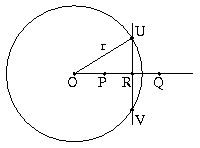
Theorem: All points within a circle lie on its circumference.

Proof after construction:

1. Given a circle around O and radius r as in the picture.
2. Furthermore, a point P ≠ O within the circle is given.
3. On the half line [OP], let Q be the point for which OP · OQ = r²
4. The center perpendicular of the line [PQ] intersects this in R and the circle in a point U.
5. Then with (3.) r² = OP * OQ = (OR - RP) * (OR + RP) = OR² - RP²
6. Using the Pythagorean theorem , OR² = r² - RU² and PR² = PU² - RU²
7. Now (6.) inserted into (5.) results in: r² = (r² - RU²) - (PU² - RU²) = r² - PU²
8. So PU = 0.

Qed

resolution

Unlike in the sketch, the point R lies outside the circle, which is why the intersection point U does not exist. This follows from the assumptions OP · OQ = r² and 2 OR = OP + OQ 0 <(r - OP) 2 = r 2 - 2 r * OP + OP 2 → 2 r * OP <r² + OP² = OQ * OP + OP² = (OQ + OP) * OP = 2 OR * OP → r <OR. The decisive mistake is made in the fourth step, where an intersection point U is assumed that cannot exist.

Fallacies from decompositions

Image to prove 64 = 65.	Image to prove 216 = 217.

Theorem: 64 = 65 and 216 = 217.

Proof by decomposition:

1. The square in the left picture has the area 8 * 8 = 64 and is divided into two triangles and two squares. From these, the rectangle below the square can be put together, which has the area 5 · 13 = 65.
2. The upper rectangle in the right picture has the area 9 * 24 = 216 and is divided into two triangles and two squares. From these the rectangle below can be put together, which has the area 7 · 31 = 217.

Qed

resolution

The diagonals in the lower rectangles are only apparently straight. If the sections were put together without being deformed, the parts would leave an area free which has exactly the content of one unit of area. This can be proven with the ray theorem . The rectangle belonging to the square should be on the diagonal ${\displaystyle {\frac {5}{13}}={\frac {3}{8}}={\frac {2}{5}}\quad \Leftrightarrow \quad {\frac {200}{520}}={\frac {195}{520}}={\frac {208}{520}}}$ which is obviously not the case. In the lower right rectangle should ${\displaystyle {\frac {7}{31}}={\frac {5}{22}}={\frac {2}{9}}\quad \Leftrightarrow \quad {\frac {1386}{6138}}={\frac {1395}{6138}}={\frac {1364}{6138}}}$ which is also not the case.

For the left decomposition, consecutive numbers f _n-1 , f _n , f _{n + 1 of} the Fibonacci sequence are suitable, because they have the identity of Cassini f _{n + 1} f _n-1 = (f _n ) ² + ( -1) ⁿ . For the dismantling of the rectangles in the right image, two successive approximations of any suitable continued fraction .

Incorrect assumptions

In the real world all bodies are more or less deformable and constraints are always more or less flexible, which limits forces and / or accelerations to finite values. The calculation of flexible systems can be made much easier by simplifying assumptions. A model of classical mechanics that is successful in this sense is the non-deformable rigid body . If this is subjected to further constraints, unrealistic infinities can quickly arise. The falling ladder is an example of this.

The ladder in the picture is leaning against a wall and standing on the floor, with its base being pulled away from the wall at a constant speed. Then the ladder hits the ground with infinite speed.

Proof:

1. Definition	:	The length of the ladder is L.	Ladder (blue) leaning against the wall and floor (black)
2. Definition	:	Let be the horizontal distance of the wall from the base of the ladder that is pulled away from the wall at a constant speed . ${\displaystyle x}$ ${\displaystyle v}$
3. Definition	:	Let be the vertical distance of the floor from the point of contact of the ladder with the wall. ${\displaystyle y}$
4th Pythagorean theorem	:	${\displaystyle x^{2}+y^{2}=L^{2}\quad \rightarrow \quad y={\sqrt {L^{2}-x^{2}}}}$
5. Time derivative	:	${\displaystyle {\dot {y}}=-{\frac {x{\dot {x}}}{\sqrt {L^{2}-x^{2}}}}}$
6. Start of speed	:	${\displaystyle {\dot {y}}=-{\frac {xv}{\sqrt {L^{2}-x^{2}}}}}$
7. When hitting	:	${\displaystyle \lim _{x\to L}{\dot {y}}=\lim _{x\to L}{\frac {-xv}{\sqrt {L^{2}-x^{2}}}}=-\infty }$

That is why the ladder hits the ground with infinitely high speed.

resolution

The cause of this fallacy is the assumption in (4.) that the ladder remains leaning against the wall and always touches it. In fact, the pull at the base of the ladder will also pull the top of the ladder away from the wall, so the contact will cease and the Pythagorean Theorem no longer applies. However, if one assumes that the top of the ladder always stays on the wall, the fallacy lies in the mathematical modeling of the physical world. Because at the end of the experiment, where the ladder is supposedly moving infinitely fast, the formulas of classical mechanics are no longer applicable, instead the formulas of special relativity must be used, including the curvature of space at high speeds.

literature

• Walter Lietzmann: Where is the mistake? - Mathematical fallacies and warning signs , 1969, 5th edition, Verlag BGTeubner

Web links

• Math jokes. Retrieved July 2, 2017 . 
• Math jokes. Aha! Jokes LLC, accessed July 2, 2017 . 
• Uwe Stephan. Retrieved July 2, 2017 . 

Individual evidence

1. ↑ Fallacias. In: Duden online. Retrieved July 2, 2017 . 
2. ↑ A. Filler: 01 Aims.pdf. (PDF) Institute for Mathematics at the Humboldt University of Berlin, accessed on July 2, 2017 . 
3. ^ ^{A b c} Edwin A. Maxwell: Fallacies in mathematics . Cambridge University Press , 1959, ISBN 0-521-05700-0 ( limited preview in Google Book Search).
4. ↑ Thilo: 1 + 2 + 3 + 4. 2014, accessed July 2, 2017 . 
5. ^ Walter Lietzmann : Fallacies . BG Teubner, 1923 ( limited preview in Google book search).
6. ↑ ^{a b} Holger Dambeck: Mathematics bizarre. Spiegel. Retrieved July 2, 2017 . 
7. ↑ ^{a b} Thomas Sauer: Counterexamples, fallacies and mathematics on the computer. (PDF) 2001, accessed July 2, 2017 . 
8. ↑ ^{a b c} Klaus Fritzsche: Mathematics tutorial for beginners . Springer-Verlag, 2016, ISBN 978-3-662-48910-9 ( limited preview in Google Book Search [accessed July 2, 2017]).
9. ^ ^{A b} Philip Spencer: Classic Fallacies. University of Toronto, accessed on July 2, 2017 (English, Canadians are considered here instead of Germans). 
10. ↑ Hermann Schubert: Mathematische Mußestunden: A collection of puzzles, tricks and entertainment tasks of a mathematical nature . Walter de Gruyter, 1967, ISBN 978-3-11-083666-0 ( limited preview in Google Book Search [accessed July 2, 2017]).