heptagon

Regular heptagon

The heptagon (also Heptagon of ancient Greek ἑπτάγωνον Heptagonon from ἑπτά hepta , German , seven ' , and γωνία Gonia , German , corner' ) is a geometric figure . It belongs to the group of polygons ( polygons ). It is defined by seven points . Unless otherwise stated, we are talking about a flat, regular heptagon (see picture), whose seven sides are of equal length and whose seven corner points lie on a common circumference.

Mathematical relationships

Formula for angle calculations

The central angle or center angle is enclosed by two adjacent circumferential radii . According to a general formula: ${\displaystyle \mu }$ ${\displaystyle r}$

${\displaystyle \mu ={\frac {360^{\circ }}{n}}={\frac {360^{\circ }}{7}}={\frac {2}{7}}\cdot 180^{\circ }=51{,}{\overline {428571}}^{\circ }}$

The sum of the interior angles of the heptagon is always 900 ° and results from a general formula for polygons in which the number of corner points of the polygon must be used for the variable (in this case:) : ${\displaystyle n}$ ${\displaystyle n=7}$

${\displaystyle \sum \alpha =(n-2)\cdot 180^{\circ }=5\cdot 180^{\circ }=900^{\circ }}$

The angle that two adjacent side edges enclose in the flat, regular heptagon is (again according to a general formula for regular polygons):

${\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {5}{7}}\cdot 180^{\circ }=128{,}{\overline {571428}}^{\circ }}$

Formula for area A

A heptagon has a clearly determinable area, which can always be calculated by breaking it down into triangles. The area of ​​the regular heptagon is seven times the area of ​​one of those triangles that are spanned by its center and two adjacent corner points.

${\displaystyle A={\frac {7}{4}}\cdot s^{2}\cdot \tan {\frac {450^{\circ }}{7}}\approx 3{,}63391\cdot s^{2}}$

or with the perimeter radius:

${\displaystyle A={\frac {7}{2}}\cdot r^{2}\cdot \sin {\frac {360^{\circ }}{7}}\approx 2{,}73641\cdot r^{2}}$

Formula for the side length s

${\displaystyle s=2\cdot r\cdot \sin {\frac {180^{\circ }}{7}}\approx r\cdot 0{,}867767478235}$

Approximate constructions

A regular heptagon cannot be constructed exactly with a compass and ruler because it is not a constructible polygon .

There are some sufficiently precise approximation constructions for practice.

The point is to get a distance which is as exactly as possible 0.86776747823 times a given radius.

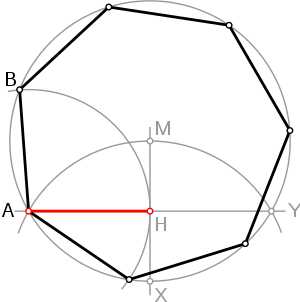
Construction according to Dürer

Construction of a heptagon

A very simple approximation construction, also known from constructions of regular polygons by Albrecht Dürer , is shown in the following drawing:

1. A straight line is drawn from the center of the circumference, which intersects the circumference at the point . ${\displaystyle X}$
2. Then you draw a circle that runs through and the circumference in the points and intersects. ${\displaystyle X}$ ${\displaystyle M}$ ${\displaystyle A}$ ${\displaystyle Y}$
3. The straight line intersects the line at the midpoint . ${\displaystyle AY}$ ${\displaystyle {\overline {MX}}}$ ${\displaystyle H}$
4. The red line is a good approximation for the side length of the heptagon. ${\displaystyle {\overline {AH}}}$
5. The corner points to are obtained by knocking off the route . ${\displaystyle B}$ ${\displaystyle G}$ ${\displaystyle {\overline {AH}}}$

Exactly the same route length can be constructed as follows:

1. Construct the regular (equilateral) triangle inscribed in the perimeter.
2. Take half of one side of the triangle as an approximation for the side of the heptagon.

In this form it was already known to the scholar Abu l-Wafa, who worked in Baghdad in the 10th century .

From the right-angled triangle AHM is calculated:

${\displaystyle {\overline {AH}}={\sqrt {{\overline {MA}}^{2}-{\overline {MH}}^{2}\;}}}$

With

${\displaystyle {\overline {MA}}=r}$ ; and ${\displaystyle {\overline {MH}}={\tfrac {1}{2}}r}$ ${\displaystyle {\overline {AH}}:=s}$

${\displaystyle s={\sqrt {r^{2}-\left({\tfrac {1}{2}}r\right)^{2}\;}}}$

${\displaystyle s=r\cdot {\sqrt {1-\left({\tfrac {1}{2}}\right)^{2}\;}}}$

${\displaystyle s=r\cdot {\tfrac {\sqrt {3}}{2}}\approx r\cdot 0{,}8660254}$

With this construction the relative error is

${\displaystyle f={\frac {0{,}8660254-0{,}8677675}{0{,}8677675}}\approx -0{,}002}$

The side length gained with this construction is a bit too short and is 99.8 percent of the true value. Or to put it another way: with a circumferential radius of approximately 57.4 cm, the error in the side length is one millimeter.

Using a coordinate system

A somewhat more complex, but more precise approximation construction is shown in the following drawing:

Alternative construction of a heptagon

1. In a right-angled coordinate system you draw a circle that has its center at the origin and runs exactly through the point with the coordinates . ${\displaystyle (0/0)}$ ${\displaystyle P}$ ${\displaystyle (2/4)}$
2. The intersection of the positive axis with the circular line is defined as the corner point of the regular heptagon. ${\displaystyle y}$ ${\displaystyle A}$
3. The straight line (green line) intersects the circular line in the immediate vicinity of the corner points and . ${\displaystyle y=-1}$ ${\displaystyle C}$ ${\displaystyle F}$
4. If you intersect the line symmetry of the line with the circle, you get an approximation for the corner point . ${\displaystyle AC}$ ${\displaystyle B}$
5. The red line or is a very good approximation for the side length of the regular heptagon. ${\displaystyle {\overline {AB}}}$ ${\displaystyle {\overline {BC}}}$
6. The corner points , and are obtained by mirroring or cutting off the side length at the circumference. ${\displaystyle D}$ ${\displaystyle E}$ ${\displaystyle G}$

Denoting with the perimeter radius , the distance of the from with and is substituted , the result is, in this construction: ${\displaystyle r}$ ${\displaystyle {\overline {FC}}}$ ${\displaystyle M}$ ${\displaystyle h}$ ${\displaystyle q={\frac {h}{r}}}$

(1)  , ${\displaystyle {\overline {AB}}=r\cdot {\sqrt {2-{\sqrt {2}}\cdot {\sqrt {1-q}}}}}$

and with the values

(2)  ${\displaystyle r={\sqrt {20}};h=1;q={\frac {1}{\sqrt {20}}}}$

surrendered:

(3)  ${\displaystyle {\overline {AB}}=r\cdot {\sqrt {2-{\sqrt {2}}\cdot {\sqrt {1-{\tfrac {1}{\sqrt {20}}}}}}}}$

(4)  ${\displaystyle {\overline {AB}}=r\cdot {\sqrt {2-{\sqrt {2-{\tfrac {1}{\sqrt {5}}}}}}}}$

(4a)  ${\displaystyle {\overline {AB}}\approx r\cdot 0{,}868269253}$

The side length obtained with this construction is a bit too long, the relative error is approximately 0.00057821133, i.e. 0.0578 percent. Or to put it another way: With a circumferential radius of approximately 199.3 cm, the error in the side length is one millimeter.

Using the given radius

A disadvantage of the above Construction consists in not starting from a directly given radius. If you want to start from the radius, the task is to find the distance between the straight line and the center point (that is the length unit of the construction with the given coordinate system) belonging to the given radius . ${\displaystyle d}$ ${\displaystyle {\overline {CF}}}$ ${\displaystyle M}$

Second approximation construction for a given radius

Derivation of the distance d

From the construction with the coordinate system and the drawing you can read:

${\displaystyle {\overline {MN}}=d}$

${\displaystyle {\overline {MZ'}}={\overline {MZ}}=2d}$

${\displaystyle {\overline {ZP}}=2\cdot {\overline {MZ}}=4d}$

This applies

${\displaystyle {\frac {\overline {PZ}}{\overline {ZM}}}={\frac {4d}{2d}}=2}$

In addition, according to the Pythagorean theorem is still

${\displaystyle {\overline {MP}}=r={\sqrt {20}}\cdot d}$

In the right triangle MZP applies according to the cathetus set

${\displaystyle {\overline {ZP}}^{2}=r\cdot p}$ and ${\displaystyle {\overline {MZ}}^{2}=r\cdot q}$

The quotient is as shown above

${\displaystyle {\frac {{\overline {ZP}}^{2}}{{\overline {MZ}}^{2}}}={\frac {p}{q}}}$

and thus

${\displaystyle {\frac {p}{q}}=2^{2}=4}$

where p and q are the hypotenuse segments. Their lengths are 4/5 and 1/5 of the radius. With this the point Z can be constructed and thus the distance d can be determined.

construction

• Construct a Thales circle over the radius . ${\displaystyle r={\overline {MP}}}$
• Set up the plumb line at a distance of from M. The point on the Thales circle obtained in this way is point Z of the right-angled triangle MZP (corresponds to point (2/0) in the construction with a coordinate system). ${\displaystyle {\frac {1}{5}}r}$
• Construct through M the parallel to the longer leg . The point of intersection with the circumference is point A. ${\displaystyle {\overline {ZP}}}$
• Plot the distance on the straight line AM from M in the opposite direction, this results in the intersection point Z '(Z', corresponds to point (0 / -2) in the construction with a coordinate system). ${\displaystyle {\overline {MZ}}}$
• The distance d = is obtained by halving the distance ${\displaystyle {\overline {MN}}}$ ${\displaystyle {\overline {MZ'}}}$
• Construct the straight line perpendicular to through N. the points of intersection with the circumference are points C and F ${\displaystyle {\overline {AZ'}}}$
• The rest follows the same as for the construction with a coordinate system.

The side length obtained with this construction and the relative error correspond to the construction with a coordinate system. It therefore also applies: With a circumferential radius of approximately 199.3 cm, the error in the side length is one millimeter.

Exact constructions

By dividing an angle into three

Construction with tomahawk (red)

If you add an extra tool to the classic (Euclidean) compass and ruler for dividing the angle into three , such as B. a Tomahawk , the heptagon but can exactly - similar to the Dreizehneck - be constructed.

With a given radius

• Construct a circle - the later perimeter of the heptagon - around a center point (O) on a baseline (AZ). One of the intersections with the circle is the first corner point (A) of the later heptagon.
• Halve the two radii of the first diameter (points Q and R)
• On the route obtained in this way, erect two equilateral triangles with the side length equal to the circle radius. (You get points K and L).
• On the baseline (AZ) from the center, mark 1/6 of the radius in the direction opposite to the corner point on the baseline (point P).
• Draw an auxiliary circle around the point obtained in this way through the two corners of the equilateral triangles that are not on the base line.
• Draw the two radii to these two points in this circle.
• Use the extra tool to divide the angle formed by these radii into three parts (e.g. Tomahawk, shown in red in the drawing) and draw the straight lines you have obtained. You cut the auxiliary circle in two more points (points S and T).
• The straight line through these points - it lies perpendicular to the base line - intersects the perimeter of the heptagon at the corners of the heptagon adjacent to the first corner point (A) (points B and G).
• Complete the missing corners by removing the sides.

Using a marked ruler

Regular heptagon, Neusis construction according to David Johnson Leisk (Crockett Johnson), see animation

Constructions using a so-called push-in ( Neusis ), e.g. B. with compasses and a marked ruler on which a special marking is applied as an additional aid, also known as a Neusis construction , were already by Archimedes z. B. to tripartite the angle and used by Abu l-Wafa in the heyday of Islam .

David Johnson Leisk, mostly known as Crockett Johnson , published a Neusis construction of a heptagon (heptagon) called in English in 1975 , in which the side length is given. For this he used a pair of compasses and a ruler on which a mark was made with regard to the side length AB .

For a given side length

• Set up the line AI perpendicular to the side length AB at point A , it is the same length as the side length AB .
• Connect point B with I, e.g. B. with a side length AB = 1, the diagonal has the value . ${\displaystyle {\sqrt {2}}}$
• Halve the side length AB , the result is point H.
• Create a vertical line to side length AB at point H.
• Draw the circular arc a with the radius BI around point B and through point I.
• Place the ruler marked with point J (distance from corner of ruler to point J corresponds to AB ) on the drawing. Turn and push the ruler until its corner to the perpendicular bisectors is applied, the marking point J rests on the circular arc a, and extends the edge of the ruler through the point A, it results in the point E.
• Connect point A with point E, the resulting angle AEH, denoted by, corresponds to a quarter of the circular angle from the heptagon. ${\displaystyle \theta }$
• Halve the distance AE , the result is point K.
• Establish a vertical line to the line AE through point K, resulting in point O.
• Draw a circle through A around point O, it is the perimeter of the heptagon.
• Use the side length AB to determine the remaining five corner points of the heptagon and finally connect the neighboring corner points with each other. This creates the regular heptagon ABCDEFG.

Regular overturned heptagons

A regular overturned heptagon results when at least one is skipped over each time when connecting the seven corner points and the chords thus created are of the same length. Such regular stars are noted with Schläfli symbols , indicating the number of corner points and connecting every -th point. ${\displaystyle \left\{n/k\right\}}$ ${\displaystyle n}$ ${\displaystyle k}$

The following gallery shows the two possible regular seven- ray stars , also known as heptagrams .

• Regular seven-pointed stars
• 

  ${\displaystyle \left\{7/2\right\}{,}\ \left\{7/5\right\}}$

• 

  ${\displaystyle \left\{7/3\right\}{,}\ \left\{7/4\right\}}$

Occurrence

architecture

The heptagon is rarely used in architecture - e.g. B. in the ground plan of the medieval church Notre-Dame de l'Assomption (12th century) in the southern French town of Rieux-Minervois . The “Hegelsaal” concert hall in the Liederhalle culture and congress center in Stuttgart , like its glass dome, has a regular heptagon-shaped floor plan.

Further examples are the bell tower of the Maria am Gestade church in Vienna , the nave of the Ketzür village church , the Africa chapel near Tholey or the baptistery of the Holy Trinity in the Croatian town of Rovinj (12th century).

• 

  Princely mausoleum (Stadthagen) ,
  heptagonal central building, view into the dome
  (source: WP)

biology

The seven star (Trientalis europaea) shows a seven-rayed flower:

• 

Others

• Coins
  • The 20 euro cent piece has seven notches to make it easier for blind people to distinguish it from other coins, similar to the ( Spanish flower ).
  • The old Spanish 200 pesetas coin shows a heptagon on both sides.
  • Likewise, the British 20 pence and 50 pence pieces have a heptagonal shape.
• The diagonals of the regular heptagon form the heptagram (seven-pointed star), which is popular as a symbol in esotericism .
• Radial engines were mostly built as 5-, 7- or 9- cylinder .
• There are fullerenes (carbon molecules) that have heptagonal substructures; the chemical compound azulene and the tropolones , benzodiazepines and other cyclic compounds contain seven-membered rings.

See also

• Heptagon after Archimedes
• Siebeneck Castle

Web links

Commons : Regular heptagons  - collection of images, videos and audio files

Wiktionary: heptagon  - explanations of meanings, word origins, synonyms, translations

Wikibooks: Heptagon  - learning and teaching materials

• Heptagon after David Johnson Leisk
• More mathematical details about the heptagon
• Heptagon with a given side length, approximation construction
• 20 euro cents

Individual evidence

1. ^ Helmuth Gericke : Mathematics in the West . From the Roman surveyors to Descartes. Springer, Berlin / Heidelberg / New York 1990, ISBN 978-3-642-74793-9 , 3.1.2.2. Albrecht Dürer: Vnterweysung der messung , p. 190–191 , side of the heptagon, Fig. 3.26. , doi : 10.1007 / 978-3-642-74793-9 , urn : nbn: de: 1111-20111119809 ( preview in Google book search [accessed on May 18, 2019] More in the table of contents p. 351).
2. ↑ Christoph J. Scriba , Peter Schreiber : 5000 years of geometry. History, cultures, people. 2nd Edition. Springer, Berlin / Heidelberg / New York 2005, ISBN 3-540-22471-8 .
3. ↑ Andrew Gleason : Angle Trisection, the Heptagon, and the Triskaidecagon . In: The American Mathematical Monthly . tape 95 , no. 3 , 1988, pp. 185–194 , 186 ff. , JSTOR : 2323624 ( math.fau.edu, FIG.1. Construction of a regular heptagon [PDF; 303 kB ; accessed on May 15, 2019]).
4. ↑ Klaus Volkert: History of the geometric construction problems I. (PDF; 1.5 MB) Lecture, University of Cologne in the winter semester 06/07. In: math.uni-wuppertal.de. University of Wuppertal, 2006, p. 20 , accessed on September 15, 2018 . 
5. ^ Eric W. Weisstein : Neusis Construction. In: mathworld.wolfram.com, MathWorld, A Wolfram Web Resource, accessed May 18, 2019.
6. ↑ Eric W. Weisstein: Regular Heptagon. In: mathworld.wolfram.com, MathWorld, A Wolfram Web Resource, accessed May 18, 2019.
7. ^ E. Albertazzi, C. Domene, PW Fowler, T. Heine, G. Seifert, C. Van Alsenoy, F. Zerbetto: Pentagon adjacency as a determinant of fullerene stability. In: Physical Chemistry Chemical Physics . 1999, 12, pp. 2913-2918, doi: 10.1039 / A901600G (PDF; with registration).