Physics of sailing
The physics of sailing (also the theory of sailing ) explains the physical principles of the fact that a sailing vehicle can move using the wind. The considerations make it possible to understand, among other things, why sailing vehicles can also go against the wind or sail faster than the wind is blowing.
An introduction to the topic is part of every sailing training.
Definitions and terms
True and apparent wind
Every sailing ship moves with the force of the wind . In shipping, a true wind is the actual wind blowing at a given location, along with direction and strength. The true wind can only be measured by fixed equipment. The apparent wind is the wind that blows on board a ship in motion. It differs from the true wind and results from a vector addition of the true wind with the ship's headwind . The picture on the right shows that the strength and direction of the apparent wind depends not only on the strength of the true wind, but also essentially on the speed of the ship and the direction of travel of the ship relative to the wind direction (course to the wind).
Courses to the wind
The course to the wind is the course (direction in which the ship is traveling) relative to the wind direction. A distinction is essentially made between the following situations:
- Close to the wind: the ship runs diagonally against the wind. Because airflow and real wind come from almost the same direction here, the speed of the apparent wind is greatest. The smallest possible angle to the wind depends on the design of the ship.
- Half wind: The ship travels roughly across the direction of the apparent (or true) wind.
- Spacer sheets: The wind blows “diagonally from behind” onto the ship.
- Before the wind: The wind blows exactly from aft (from behind) onto the ship. The speed of the apparent wind is the lowest here.
- In the wind: The wind is blowing straight from the front of the ship. A normal sailing ship cannot go in this direction.
Depending on the course to the wind, the sailor chooses the position of the sails. As a rule of thumb, the tree halves the angle between the midship line and the angle of incidence of the wind. Upwind sail and peppers very dense brought on downwind sails are almost querschiffs. By trimming the sails , the sails are precisely adjusted to the prevailing wind and sea conditions.
Aerodynamics of sailing
Propulsion of a sailing ship
A sailing ship is propelled by two effects: by wind pressure on the sail and by air flow around the sail, which pulls on the sail due to the negative pressure. In practice, both effects usually overlap, with one or the other predominating depending on the course to the wind. When the ship is moving, the counterforce to propulsion is essentially the water resistance that acts on the hull. The main propulsion results from the transmission of the wind pressure to the mast or sheets guiding the sails, and the force is in turn transmitted to the hull . The fuselage is practically "pulled along".
When the wind blows against it, the sail takes on a curved shape ( belly ) and develops a force that is proportional to the product of the sail area and the square of the wind speed . The force acts perpendicular to the surface of the sail in the leeward direction . In addition to the shape and size of the sail and the wind speed, the angle of attack of the wind on the sail also has an influence on the magnitude of the force . Depending on the angle of attack, either the component propulsion by resistance or the component propulsion by buoyancy predominates (Diagram 1).
Wind pressure on the sail
If the wind hits the sailing ship from behind (on a downwind course ) or diagonally behind (on a downwind course), the sailing ship is driven by the resistance that the sails oppose to the wind. The air flow is interrupted and the wind tries to "push away" the resistance. This type of propulsion is best used by the square sails formerly used on tall ships . Tall ships, too, drove faster on a downwind course than on a downwind course, as most of the sails in the latter are in the slipstream of the rearmost sails. Modern sailing ships with sling sails are not particularly well suited for propulsion by drag, as the sling sails lack sail area, especially in the upper, more effective area. In order to compensate for these disadvantages, large, bulbous sails such as spinnakers or gennakers are also used in the course area Before the Wind to Half Wind .
Wind flow on the sail (wing effect)
Sailing ships are able to sail diagonally against the wind and cruise up . This enables goals to be achieved that are downwind. While having fore- the greatest efficiency. In terms of flow technology, sails behave similar to the wing of an airplane. The curvature (the belly) of the sail causes complex aerodynamic processes and currents around the sail. The different flow velocities on the windward and leeward sides of the laminar flow past the sail lead to pressure differences that add up to a total vector that, based on the wing, i.e. the sail, points leeward and forwards. This requires a force. This force is partly converted into propulsion and partly into drift to leeward and - through the resistance of the keel or sword under water - into heeling (inclined position of the ship). Since the sails only provide lift (or propulsion) when there is flow around them, one speaks of dynamic lift .
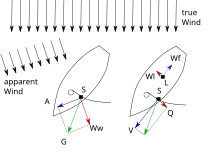
The adjacent diagram 2 explains the forces that act on a boat sailing close to the wind. The illustration on the left shows the force G that the wind exerts on the sail. The wind power can be broken down into lift A and drag Ww . With an optimal flow against the sail, the lift is about five times as great as the air resistance. The shape of the boat hull and the lateral plan reduce the lateral movement and optimize the propulsion (right illustration, the lateral resistance Wl is much greater than the form resistance Wf ). The resulting transverse force Q on the sail leads to heeling in monohull boats , which must be compensated so that the boat does not tip over (see section on stability ). It should be noted that the wind force G acts on the sail pressure point S, while the counterforce of the lateral plan Wl acts on the lateral pressure point L. By correct setting of the sail and adapted heel, the two forces can be balanced in such a way that the boat is neither luffy nor eager to leeward and only the steady forward movement with constant heel remains.
The two acting forces can also be determined numerically approximately:
with K = conversion constant (0.5 for propulsion, 1.32 for lateral force, also depending on the course to the wind), A = sail area in m 2 , v = speed of the apparent wind in m / s, ρ L = density of the air ( ~ 1.204 kg / m 3 ). The result W is the acting force in Newtons . Example: A boat with a sail area of 35 m 2 generates a propulsion of 263 N with an apparent wind of 5 m / s. If the boat sails at 6 knots (3.09 m / s) this corresponds to a wind power of 0.81 kW or 1.09 hp .
The yacht accelerates until the propulsion and drag forces are balanced. The form resistance is the resistance that arises from the fact that the boat hull has to push it to the side while driving through the water. The bow and stern waves running away show that energy is being consumed. The frictional resistance is created by the friction between the water and the hull of the boat. It can be reduced by suitable surface coatings , which at the same time also reduces harmful growth on the hull. Ship designers try to keep form drag and frictional drag as low as possible by designing the boats to be streamlined and keeping the area wetted by the water small. The air resistance occurs in all parts of the boat that are above the waterline: the surface hull, superstructures, the rig and the crew. On courses in front of the wind, however, any air resistance helps propulsion.
The propulsion on the sail - and thus the propulsion power and the speed of the boat - is decisively influenced by the angle between the sail and the wind, the so-called angle of attack. If this angle is too small, the sail begins to flap (flutter). If the angle is too big, the air flow on the leeward side of the sail breaks off, air vortices are created and the lift collapses. Trimming sets the correct angle between the sail and the wind.
The angle of incidence of the wind is not only determined by the course angle of the ship to the actual wind, but also by its own speed. The effective wind relevant for the sails, the apparent wind, will always come in earlier than the true wind. Since the speed of the apparent wind also increases with the boat speed, it is possible to sail faster than the wind . Because of the increasingly forward incoming wind with increasing speed, you will have to drive the sails ever closer. From the crew's point of view, a fast sailing ship therefore very often travels close to the wind, even when the true wind comes in from the aft.
Hydrodynamics
In addition to the rig, as indicated above, the underwater hull is also important for the sailing characteristics of a ship. The designer determines the so-called lateral plan via the longitudinal plan . This is the lateral resistance surface of the underwater hull, with which the drift is prevented. The lateral plan also includes the keel, rudder and any guide fins. The lateral pressure point is the point at which the transverse forces can be thought of as combined. However, it is not static, but changes with the heel of the ship. The more the ship heels, the further the lateral pressure point moves forward, because mainly the bow penetrates deeper into the water, but the deep keel and the rudder rise higher and higher.
The dynamic forces on the underwater hull are shown in diagram 5 on the right. In fact, the righting effect of the keel is not responsible for the force Wl in the windward direction, it only counteracts the torque around the longitudinal axis. The lateral force to windward is built up by the fact that the keel fin also acts like a wing. The angle of attack is the drift angle (angle between the adjoining course K and course through the water K ', indicated with or in the literature ). The lean body theory also provides an interesting connection. The hydrodynamic lift of the keel is determined as
with L = buoyancy, C = conversion constant , = density of the water, = speed through the water, T = draft, = draft of the hull. From the formula it follows that with a first approximation the buoyancy does not depend on the area of the keel, but only on the square of the draft. This means that the keel can be shortened without reducing the buoyancy, which corresponds exactly to the evolution of the keel shapes over time. The shortening has the advantage that it reduces the frictional resistance of the trunk. The disadvantage, however, is the lower course stability and the more nervous behavior at the rudder, as well as the challenge for the designer of safely introducing the large transverse forces on the small contact surface of the keel into the hull.
In addition to the buoyancy on the keel, the buoyancy on the rudder must also be taken into account, because this also acts as a symmetrical aerodynamic wing, only with a smaller area. Usually the rudder is also shallower than the keel, but there are mainly practical reasons for this: In the unfortunate event of a grounding, the massive keel can withstand significantly more than the comparatively filigree rudder blade.
As already stated above, the shape of the underwater hull has a significant influence on the sailing properties. The hull should be as streamlined as possible so that the ship moves smoothly through the sea. In keel boats, the keel weight should be as heavy as possible and attached as low as possible in order to maximize its leverage and to maximize the hydrodynamic lift forces. It is the task of the boat designer to weigh these partly contradicting requirements against each other and to adapt them to the intended use of the boat. Fast regatta boats today have a very flat hull with a deep keel, which means that they can partially plane . Cruising sailors prefer somewhat rounder and deeper hulls with a shallower draft, as these offer additional living space, glide more gently through the waves and also smaller harbors and bays can be entered. The generally larger total weight of cruising yachts - in relation to the boat length - also increases comfort, as a heavier boat dances less in the waves. The disadvantage is the great weight when there is little wind, because such heavy boats can only be sailed sensibly from a certain wind strength.
Interactions of the water with the hull of the boat
Wind waves
The sailing ship moves at the boundary layer between air and water. The phenomenon called “surface waves” in the physical sense, or simply “waves” in common parlance, has a significant influence on the movement of a ship. For the sailor they are often just annoying, as they can slow you down if they hit the bow from the front and often flood the deck as well. They also cause dynamic movements ( yawing around the vertical axis, rolling around the longitudinal axis, pitching around the transverse axis), which are uncomfortable and can cause seasickness . The energy of a wave can capsize a ship , especially if it hits directly from the side, because the kinetic energy of the moving water can be enormous due to its mass alone.
Wave system generated by the ship
While the effect of the wind waves on the ship is obvious to any observer, this is not true of the waves that the ship itself generates. First of all, if the water is sufficiently deep and the water is shallow, a ship creates a wave system that always looks the same (see video). The form of this system is surprisingly independent of the speed of the ship and the density of the liquid. The wave system opens at an angle that goes through
given is. It is a purely geometric property of waves that results from the fact that the wave pattern is stationary relative to the moving ship. In addition, the so-called dispersion relation for deep water waves plays a role:
is also referred to as the phase velocity of the waves. This can be seen as a numerical equation
write or with units more common in seafaring
which puts the phase velocity of the waves in relation to the wavelength.
The above formula is also often written as
with the waterline length L of a ship instead of the wavelength . This is precisely what is known as the trunk speed . In connection with the trunk speed, the so-called Froude number is also often mentioned . This is a dimensionless number that puts the wavelength of the wave system generated by the ship in relation to the length of the ship:
with v s = ship's speed, g = acceleration due to gravity , L = waterline length. The speed of the ship is equal to the phase speed of the water. By inserting the right term from equation (*) this becomes:
The Froude number can now be used to compare the wave systems of different ships. A ship traveling with a Froude number less than 0.4 sails below its hull speed, because the wavelength of the wave system generated is shorter than the waterline length. When the Froude number 0.4 is reached, the water resistance increases exponentially, because the ship now creates a wave system that is exactly one wavelength long. At the bow there is the wave mountain, at the stern the valley. In order to be able to accelerate further, the ship has to “run over” its own bow wave. This is exactly the point at which a glider - assuming sufficient propulsion power in the form of wind energy - can transition to planing. However, this is only the case with light, flat-hulled boats.
Windward and empty greed
Since a boat is always designed in such a way that the sail pressure point S lies in the leeward position of the lateral pressure point, the force couple propulsion V and form drag Wf creates a torque to windward. This increases the more the boat heels, because this increases the lever arm. On the other hand, the force couple consisting of the transverse force Q and the resistance of the lateral plane Wl, which generates a leeward torque, acts . The torque increases if the sail pressure point moves too far forward, for example because the sail areas of the various sails are not in the correct relationship to one another.
With a correctly constructed ship and correctly adjusted trim of the sails, the two forces are balanced and the ship moves in a straight line even with the rudder fixed. Sailing ships are deliberately designed in such a way that they become more and more luffy with increasing heeling - for example due to increasing wind. By luffing up, the heel is automatically reduced again, and if no countermeasures are taken, a sunshot will follow: the bow turns into the wind and the ship stops. If the boat were to break leeward in such a case, the heel would increase significantly (because the wind then press across the sail) and provoke a capsize . A ship that is leeching on a space sheet course also favors a dangerous jibe .
stability
An essential task of the keel or sword is to oppose the laterally acting wind pressure on the sail with a resistance under water in order to reduce the drift to leeward . The resulting lean angle of the boat is called heeling . A boat can also be heeled by rough seas. The stability of a boat is understood as its ability to compensate for this heeling and to return to an upright position on its own. This can be done in two different ways: on the one hand through dimensional stability, in which the hull shape of the boat favors a return to the starting position, and on the other hand through weight stability, in which a low-lying ballast keel forces the boat back into the upright position.
In weight-stable yachts , the ballast keel generates an erecting torque that becomes stronger with increasing heel. Such a boat has a low initial stability, but a high final stability, and can only capsize under very severe wind and sea conditions . Since the heel also reduces the wind pressure in the sail, a large lean angle is not critical for the boat alone - but potentially uncomfortable for the crew. The shape of the hull also prefers a certain heel angle so that the speed can increase again by reefing in good time . In dimensionally stable boats, such as a dinghy , the heel is compensated for by the buoyancy of the hull and the crew weight is shifted to windward ( riding out ).
dynamic behaviour
The previous considerations were based on the assumption that the boat is in a static driving state or at least that it will regain it after a brief imbalance. However, this is not the case in several cases, for example because the boat should change course or because it is made to "dance" in rough seas .
Change of the moment equilibrium: Discard
The first point in time at which the torque equilibrium changes and, as a result, the uniform driving state of the previous sections is finally reached, is the discarding. We look at a boat that is moored to the jetty with the sails set. The speed through the water is therefore zero, which means that the hydrodynamic buoyancy of the keel is also zero. The wind blows at a constant speed in an offshore direction ( casting off maneuvers under sails with an onshore wind are challenging enough in themselves). A leeward force acts on the ship, but in this state it only leads to heeling.
If the mooring lines are now thrown off, the wind initially pushes the boat away from land. As a result, it also picks up speed forwards at the same time, because the bow is pushed away faster than the stern (when driving slowly). This creates the current around the keel, which results in the hydrodynamic side force that the keel has to oppose the sail pressure so that the ship travels straight ahead when heading upwind. The state of equilibrium is reached when, as can be seen in diagram 2, the underwater force of the keel ( ) and the buoyancy force of the sail ( ) are in balance.
Change of the moment equilibrium: turning
In addition to berthing and casting off, the most important maneuvers on a sailing ship are turning and jibing . During these maneuvers, windward and leeward change their places and the sails are then on the other side of the boat. From a physical point of view, this means that the direction of the lift vector of the sail and that of the hydrostatic lift vector are exchanged.
Let us assume that the boat is sailing steadily on the starboard bow. The turn is initiated by the helmsman clearly laying the rudder to windward (port). This creates an angular momentum, because the buoyancy force of the rudder blade now points to leeward due to the large angle of attack (in straight travel, the buoyancy force of the rudder blade points slightly to windward to compensate for the boat's greediness). The boat responds promptly and luffs until the sails collapse (kill), and if there is enough momentum, it continues to turn until the wind from the other side catches the sails. The helmsman must now give "support rudder", i. i.e. steer against the turning movement in order to absorb the turning movement of the boat with a rudder lift in the new empty direction. If the turn was carried out quickly, there is still enough speed in the boat so that the hydrodynamic buoyancy of the keel immediately arises on the new course, of course now in the new windward direction. The wind fills the sail and develops its buoyancy.
The lift forces of the keel and sail have now changed their direction by 180 °, but the total forces have not, because the new course (the direction of the propulsion vector) has only changed by the turning angle of typically around 90 °.
Vibratory movements
A ship in motion is accelerated by waves in the longitudinal, transverse and vertical directions, as well as around all three axes. The first thing that is interesting is the vertical acceleration, which leads to a vertical diving oscillation when the boat is raised and lowered by waves. The boat itself reacts like a spring, because the deeper it goes, the greater the buoyancy that wants to bring the boat back into its normal position. The natural frequency of the ideal boat depends on the mass m and a spring constant k dependent on the hull . For a real boat supplies
already quite good estimates ( = area of swimming water line , = density of water). As a rule, the wave frequency will not correspond to this natural frequency, which, from a physical point of view, amounts to the problem of an externally excited vibration system. In boat building, it is desirable to avoid possible that the boat excited with its natural frequency can be, for a suggestion of a vibrating body at its natural frequency leads to a very high amplitude , which may well be higher than that of foreign generating system (in this case the waves). Ships with a very low natural frequency (such as catamarans with a small waterline surface) are called "wave-piercing" ships because they pass through the waves.
Equivalent considerations can also be made for rotary movements. Again, there are wave patterns that can make the boat roll much more than the height of the waves would suggest. The angular frequency of the rolling oscillation is formally represented as
with = metacentric height (approximately the distance between the point of action of the lift and the center of gravity) and = moment of inertia. For reasons of stability, a large one would be desirable, because capsizing is less likely with such a yacht . It takes the vertical swimming position again very quickly. From a dynamic perspective, however, this can also be a considerable disadvantage, because a rapid (back) movement of the ship causes great forces in the rigging, which the dimensioning of the same could not provide. There are several examples in the literature of delimbing through too stiff (too “stable”) constructions.
literature
- Wolfgang Püschl: Physics of sailing. 1st edition, Wiley-VCH, Weinheim 2012, ISBN 978-3-527-41106-1 .
- Joachim Schult: Sailors Lexicon. 13th edition, 2008, ISBN 978-3-7688-1041-8 .
- Thomas Bock (staff), Petra Krumme (editor): seamanship. Yachting manual. 30th edition, Delius Klasing, Bielefeld 2013, ISBN 978-3-7688-3248-9 . (Since 1929 it has been published by the German High Seas Sports Association "Hansa" with changing employees , initially with the subtitle Manual for Sailors (and Motorboat Drivers), since the 13th edition in 1969 as a manual for yachting. )
- Ross Garret: The Symmetry of Sailing. Sheridan House, Dobbs Ferry 1996.
Web links
Individual evidence
- ↑ The literature disagrees as to whether a half wind course should refer to the true or the apparent wind.
- ↑ a b c seamanship. 28th edition, p. 157 f.
- ↑ Joachim Schult: Segler-Lexikon. Keyword wind power F = C T · 0.615 · v 2 · A with C T between 1.0 for downwind courses and 1.5 for upwind courses.
- ↑ Special information for regatta sailors and the antifoulings used for regatta boats . Retrieved December 26, 2012.
- ↑ a b Joachim Schult: Segler-Lexikon. Keyword "Lateral Plan".
- ↑ Wolfgang Püschl: Physics of sailing. P. 16 ff.
- ↑ Wolfgang Püschl: Physics of sailing. P. 108 f.
- ↑ Wolfgang Püschl: Physics of sailing. P. 124.
- ↑ After Ross Garret: The Symmetry of Sailing. In Wolfgang Püschl: Physics of sailing. P. 169 f.
- ↑ After Ross Garret: The Symmetry of Sailing. Adapted from Wolfgang Püschl: Physics of sailing. P. 171.
- ↑ Wolfgang Püschl: Physics of sailing. P. 173.
- ↑ Wolfgang Püschl: Physics of sailing. P. 177.