Mass (physics)
| Physical size | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Surname | Dimensions | |||||||||
| Formula symbol | ||||||||||
|
||||||||||
The mass, also obsolete rest mass, is a property of matter . Both the gravitational forces acting on a body and the gravitational forces caused by it are proportional to its mass. It also determines the inertia with which the state of motion of the body reacts to forces. This double role of the mass is the content of the equivalence principle .
In most physical size systems it is one of the basic sizes . It is in accordance with the international system of units in the unit kg indicated. The formula symbol is mostly .
The mass is an extensive quantity . If a system has a mass other than zero, then the two physical quantities associated with the movement, momentum and kinetic energy , are proportional to it. Furthermore, the mass of a system determines its rest energy . Due to the equivalence of mass and energy , the two quantities mass and rest energy only differ by the constant factor ( speed of light squared). The mass of a body is independent of its movement.
Outside of physics, mass is also referred to as weight , especially in everyday language . It should be noted that this word can also stand for the related, but not identical, meaning weight .
Development of the concept of mass
Mass in classical mechanics
The physical term mass was coined in the middle of the 17th century when Johannes Kepler , Galileo Galilei , Isaac Newton , Christiaan Huygens (and others) laid the foundations of modern natural science with the study of the movements of bodies on earth and in the sky . From observations of how the speed of a body changes due to impact or the application of force, it was concluded that every body has an unchangeable quantity that causes its inertia. This corresponded to the older philosophical term "quantitas materiae", which was supposed to describe the amount of matter contained in a body . Newton defined this size by starting from the density and volume of a body, and from then on referred to it as “mass”. Accordingly, Newton was guided by the then common understanding that pure matter existed in the form of small particles of the same nature, which with ether-filled spaces of different sizes form the various real bodies. From this the concept of mass in classical mechanics finally developed . Its exact characteristics are:
- Inertia: Due to its mass, a body opposes a force that changes its speed in size and / or direction: The speed change takes place in the direction of this accelerating force and is inversely proportional to the mass.
- Gravitational charge: Due to their masses, two bodies attract each other, whereby the direction of this attractive force lies along the connecting line and its strength is proportional to the masses of both bodies.
- Invariant measure of the amount of matter: The mass of a body does not depend on its speed. I.e. it remains the same if you change the frame of reference in which the body is viewed. In classical mechanics, this change means that the coordinates of the body are converted using a Galileo transformation .
- Additivity: The mass of a composite body is the sum of the masses of its individual parts.
- Conservation of mass: In all physical processes, the total mass is retained.
Property no. 1 is part of Newton's second law and defines the meaning of the physical quantity mass through its inertia, but it assumes the definition of the quantity force . Property No. 2 is part of Newton's law of gravity , which became the basis for the precise description of gravity and planetary motion . It provides the required force definition by specifying the gravitational force and thus turns all other forces into measurable quantities by comparison with the weight force resulting from gravitation. The statement contained in the law of gravitation that it is the mass defined by inertia that causes gravity is called the equivalence of inert and heavy mass . Properties No. 3 and 4 of the mass result in Newtonian mechanics as a consequence of the defining property No. 1. The conservation of mass (property No. 5) is a fact of experience, initially from the field of mechanics, its validity at the end of the 18th century (especially by Antoine de Lavoisier ) could also be extended to the chemical processes. Together, the last three properties correspond exactly to the idea of an indestructible substance of which the material world is made.
Until about the middle of the 18th century, the important conservation quantities momentum and kinetic energy were worked out, which are connected to the mass of a body in motion:
- Movement quantity : In addition to the speed, a second directed quantity, the momentum, belongs to the movement of a body . Its amount is proportional to the mass, its direction is parallel to the speed. With each process, the vector sum of the impulses of all bodies involved is preserved.
- Kinetic energy: The movement of a body also includes an undirected conserved quantity, the kinetic energy . It is proportional to the mass and is zero when the body is at rest. In each process the total energy remains, i. H. the sum of kinetic energy and all other forms of energy.
These two conservation laws for momentum and energy are fundamental for both classical and modern physics and, in the given formulation, apply exactly in both areas. On the basis of this, one can give a new definition of mass, which in the end corresponds to the five properties mentioned above, but does not already require any of them. To do this, you also need a precise definition of how the description of a physical process is to be changed when you switch to a moving reference system. There is no need to resort to the concept of force, which, according to Ernst Mach , Gustav Kirchhoff , Heinrich Hertz and others , was criticized in the 19th century as unsuitable for a basic concept that was satisfactory in terms of the theory of science.
Change to modern physics
In the context of classical physics, and thus also in everyday life, all five of the above-mentioned properties of the mass apply. In the of relativity and quantum physics influenced modern physics they only approximately valid.
Hendrik Lorentz discovered at the beginning of the 20th century that, for electrodynamic processes, a change in the reference system does not have to be carried out with the aid of the Galilei transformation, but with the Lorentz transformation . Albert Einstein realized that this applies to every physical phenomenon, including mechanics. This makes the relationship between the force and the change in speed caused by it far more complicated than assumed in the classical definition of mass (property no. 1). It also follows that when a system changes its internal energy (this is the energy content that it has in its rest system), its mass changes proportionally. The mass of a composite body therefore depends not only on the masses of its constituent parts, but also on the kinetic and potential energies that they have when the body as a whole is at rest. A body loses mass when it is assembled from individual components, when binding energy is released, this is referred to as a mass defect . Conversely, its mass increases when its components move more violently, such as when it is heated. The relevant energy values are always obtained by multiplying the value of the mass or the change in mass by the square of the speed of light . This conversion factor is a universal constant. Therefore changes in mass and energy cannot be separated from one another at all, rather there is a general equivalence of mass and energy .
The equivalence of mass and energy always applies. A body at rest has to be assigned a rest energy according to its mass (Einstein equation). Conversely, according to the same equation, a system must always be assigned a mass if it has rest energy, i.e. H. if it still has energy at zero total momentum. This usually remains hidden in everyday life, but is particularly evident in the mutual destruction ( annihilation ) of two mass-affected elementary, considering the process in their center of mass system, so in the rest of the Zweiteilchensystems. Annihilation radiation arises with an energy that is given by the rest energy of the vanished two-particle system. It has a total momentum of zero, just like the two-particle system before. The same mass must be assigned to this radiation field as to the two-particle system, because no difference can be determined. Even massless objects (e.g. two or more light quanta ) can form systems that have a mass.
The classical properties of the mass given above can therefore only remain approximately valid, namely for the classical or non-relativistic limit case, i.e. H. for solid bodies with low speed. According to the requirements of the Special and General Theory of Relativity, they have to be reformulated as follows:
- Inertia: Due to its mass, a system opposes a force that changes its speed in magnitude and / or direction: the change in speed is inversely proportional to the mass, but its direction and magnitude also depend on the magnitude of the speed and the angle between the force and the speed.
- Gravitational charge: Two systems attract each other due to the masses, energies and impulses they contain.
- Invariant quantity mass: The mass of a system does not depend on its speed; it remains unchanged if one changes the reference system in which the system is viewed by means of a Lorentz transformation.
- Additivity: The mass of a composite system is equal to the sum of the masses of its individual parts, minus the mass equivalent of the binding energy that would have to be added for the complete separation of the bound individual parts, plus the mass equivalent of the kinetic energies of those individual parts that belong to the system as free particles .
- Energy conservation: The sum of all energies is retained in all processes. The rest energies associated with the masses are contained in it. The sum of the masses alone is not always preserved.
In the end, the mass is generally defined by means of the equation through the rest energy. Thus the mass is a Lorentz invariant , just as the mass defined by Newton is a Galileo invariant . Therefore, both definitions of mass not only agree in value, but also share a deep-seated relationship, which also makes their difference clear: Both definitions of mass result in the same way from the conservation law for the momentum, once it is in the rest system formulated and a second time in a reference system that moves against it (see below). If one completes the transition from one description to the other with the only approximately correct Galileo transformation, one arrives at the classical concept of mass; if one carries out it with the Lorentz transformation, one arrives at the modern concept of mass.
The original meaning of mass as a measure of the amount of matter can no longer be maintained.
Obsolete: "relativistic mass" and "rest mass"
With the introduction of the theory of relativity, the need arose to adapt the concept of mass, based on classical mechanics. About the equivalence of mass and energy z. B. Lorentz introduced a so-called "relativistic mass" of a system, which after multiplication with the factor is equal to the sum of rest energy and kinetic energy. The relativistic mass was subsequently defined as mass . In contrast to this, it was necessary to designate the "rest mass" of a system as the mass that results from the energy for the system at rest, which means that it has no kinetic energy. The kinetic energy of a system, however, depends on the reference system from which it is viewed. The relativistic mass is therefore not suitable for universal and direct characterization of the system.
In the first half of the 20th century, the various designations existed side by side in specialist circles , until the modern definition that is valid today prevailed: mass is a system property that is independent of the reference system. It is the mass belonging to the rest energy, equivalent to the earlier "rest mass". The term "rest mass" is therefore obsolete. Einstein himself justified the choice of words in 1948:
“It is not good to speak of the mass of a moving body, since no clear definition can be given for it. It is better to limit yourself to the "rest mass" . You can also use the expression for momentum and energy if you want to specify the inertia behavior of rapidly moving bodies. "
The now historical definition of mass in the form of relativistic mass, on the other hand, persists in popular scientific literature and textbooks. It is also reflected in the popular spelling of the special theory of relativity , which is correct, however , with as rest energy and as mass . It is therefore not possible to add mass to a system through acceleration alone.
Definition of the mass using conservation of momentum
The derivation of the concept of mass from the conservation of momentum illuminates both differences and similarities between classical and relativistic physics. The result of the derivation is that if each body can be individually assigned a variable parallel to its velocity , so that the sum of these two variables remains constant in the case of an inelastic collision , then there must be a value for each body that is independent of the reference system with which (classical) or (relativistic) applies. It is called the momentum and the mass of the body. This gives an independent definition of the mass that is based solely on conservation of momentum. It also follows that in addition to the sum of the impulses in classical physics, the sum of the masses is also preserved, but in relativistic physics the sum of the quantities , which (except for the universal factor ) indicates the energies of the individual bodies.
For this derivation we consider the completely inelastic collision , i.e. H. two bodies ( ) that move towards each other and unite into one ( ). The pulses ( ) are each parallel to the speed ( ), with initially unknown factors ( ). Conservation of momentum means:
This gives the equation:
The factors can also depend on the respective speed in an as yet unknown way. Sure they are but the same in the event that both bodies are designed exactly alike: . In this case, if the collision is considered in the rest system ( ) of the body formed in the collision :
Therefore it follows that in this reference system the velocities of the two same impacting bodies must be opposite and equal:
However, the two velocities are not oppositely the same if the same shock is considered in a reference system moving with the velocity . After the impact, the body moves with speed . The equation for conservation of momentum is now:
This contains the speeds of the two impacting bodies in the moving frame of reference.
- Consideration with classical physics
According to the Galileo transformation valid in classical physics, the simple addition of the speeds applies
and consequently
This equation between the three speeds is compatible with the above equation between the three pulses only if
- such as
Because with two different factors , a vector that is too parallel cannot result. From the first equation in the previous line it follows that the factor is the same for all speeds. It is identical to the mass known from the older definition. This generally applies (with the usual symbols):
With knowledge of this equation, the consideration can be generalized to the case of different masses . Insertion into the equation of conservation of momentum leads to the result:
Accordingly, in classical mechanics, the mass is an additive conservation quantity.
- Consideration with relativistic physics
In this case, the Lorentz transformation must be used instead of the Galileo transformation. Then the relativistic addition theorem applies instead of the simple addition of the velocity vectors . From this it follows (after a long calculation): It is not parallel to , but the vector . Multiplied by a constant, which is already referred to here in advance , the total pulse must result. Consequently, the two impulses of the bumping body are through
given. For small velocities, where it can be assumed, this goes over into the non-relativistic formula , with which the constant factor actually turns out to be the mass in the relativistic definition. The equation for conservation of momentum is now
and thus again enables the determination of . It turns out that the mass in relativistic mechanics is not an additive conservation quantity, because the following applies:
According to this equation, the energy calculated according to the relativistic formula is an additive conservation quantity.
Positive and negative effective mass
The mainly in solid state physics common effective mass of particles of a size that is similar in some respects to their mass. It is obtained from the dispersion relation of the particles by approximating them in a certain range using the non-relativistic equation . In contrast to the real mass, the effective mass can depend on the momentum and can even become negative in certain value ranges.
Mass bowl
As the momentum of a particle of mass moving with speed , in relativistic physics
is (derivation see quadruple momentum), the energy and the momentum depend on the mass through the energy-momentum relationship
together. In the four-dimensional space of all conceivable energy and momentum values, according to this equation, the physically possible energies of a particle of mass lie on a three-dimensional surface, the so-called mass shell. It is a hyperboloid ( describes a hyperbola in the - plane).
The energy-momentum relationship also applies to photons . They are massless and always move at the speed of light. The energy of a photon is, apart from one factor, the amount of its momentum, its mass disappears:
units
The SI base unit of mass is the kilogram with the unit symbol kg. In most industrialized countries, the use of the kilogram as a unit of mass is legally required in connection with business transactions. Historically, countless weights were in use, some of which were unspecific depending on the area, time and product , corresponding to dimensions , packing units , load capacities and other things and are therefore difficult to specify precisely; see old weights and measures .
To indicate the mass of atoms and molecules is atomic mass unit (amu) widespread.
In particle physics, it is customary to give an indication in electron volts divided by the square of the speed of light (see mass-energy equivalence ).
Measurement
Direct mass determination
The direct measurement of the mass takes place on the resting body by comparison with a reference mass. Two masses are the same if they have the same weight in the same gravitational field . This can be checked with a beam balance . The strength of the gravity field is irrelevant, it just has to be different from zero and the same in the locations of the two bodies. To determine the unit of mass, see kilograms .
Indirect mass determination
The mass can also be determined using forces and accelerations. In Newtonian mechanics , every change in motion is proportional to the force that caused the change in motion (see below:) . Mass is therefore the constant of proportionality between force and acceleration:
The acceleration indicates the change in speed caused by a force .
Example of the inert mass: When a body by the constant force within the time interval for faster, so its acceleration is:
Its mass is then:
Example for heavy mass: Due to the gravitation of the earth, freely falling bodies become with it
accelerated. A body that is attracted by weight on the surface of the earth has mass
Related sizes
In Newtonian mechanics, mass is an extensive quantity . This means that two bodies of mass have a total of twice the mass . Intensive sizes do not change when the system is doubled. The following intense quantities are related to the mass:
- So one can calculate the mass of a homogeneous body if its volume and density are known.
- If you relate the mass to the amount of substance , you get the molar mass with the SI unit
Classical physics
In classical physics , mass is a conserved quantity . This means that the mass does not change in a closed system. If, for example, a piece of wood burns, then, according to classical physics, the resulting combustion gases and the ashes after combustion have exactly the same mass as the piece of wood and the oxygen in the air before combustion. This is taken as a self-evident empirical fact without giving any justification.
Nor explains classical mechanics , the equivalence of inertial and gravitational mass .
As a heavy mass is referred to both the source of the gravitational force and the "gravitational charge". The force exerted by the mass on the mass is
where the masses are thought to be point or spherical and the vector is from to . is the gravitational constant , a natural constant .
In Newtonian mechanics, inertial mass is what opposes acceleration. In order to change the state of motion of a body, one must therefore exert a force . The greater this force, the more the momentum changes. This is expressed by Newton's 2nd axiom , the principle of action:
With the momentum for bodies with constant mass, this results in the equation of motion for "force equals mass times acceleration", the "basic equation of mechanics":
Here the inertial mass is the proportionality factor between force and acceleration.
Special theory of relativity
Definition of mass as a Lorentz invariant
In the special theory of relativity, the mass is defined in such a way that it is a Lorentz invariant quantity that, in the limiting case of small velocities, corresponds to the mass of classical physics. To do this, one starts from the energy-momentum relation of a system and rearranges it according to the mass :
Therein is the energy and the magnitude of the momentum of the system.
The quantity defined in this way is therefore the norm of the relativistic four-vector (see energy-momentum vector ) divided by the constant , hence a Lorentz variant . This quantity corresponds to the mass defined in the scope of classical mechanics, i.e. H. for speeds that are small compared to the speed of light. This can be seen from the relationship between momentum and speed:
The factor is also called the Lorentz factor .
In the special theory of relativity, the momentum is not the product of mass and speed, as is the case with Newton . The Newtonian formula is only valid as an approximation in the non-relativistic limit case.
Relativistic mass
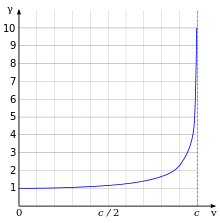
In order to still be able to retain the Newtonian formula, the term relativistic mass was used
introduced so that . In this context, the mass is often written as and called "rest mass" (see above under "Word usage" ), because applies to
- .
The term relativistic or relativistic variable mass is still used in popular literature today. In technical jargon, however, it is increasingly avoided so that the term mass can be used consistently for a property of the particle or system that is not influenced by the observer. In addition, the relativistic mass leads to correct results instead of only in the equations for the momentum and for the relativistic energy . Used in Newton's law of gravitation, however, it produces wrong results, just as in Newton's 2nd law, if you write it as .
The last-mentioned deficiency results from the definition of force as the change in momentum over time, i.e. in the special theory of relativity:
If one forms the size and thus the size from this
this is how you can change after the acceleration :
Accordingly, the acceleration basically also has a component in the direction of the speed. However, this is negligible for low speeds . Then this equation corresponds to the basic equation of Newtonian mechanics:
You can see, however, that the direction of the acceleration is only parallel to the force if it acts exactly perpendicularly or parallel to the speed. Otherwise the acceleration also has a component that is parallel or anti-parallel to the speed and increases with increasing speed. In addition, the acceleration is lower by a factor if the force acts in or opposite to the direction of the speed than perpendicular to it. The acceleration a force causes depends on the speed of the body in terms of size and direction. There is no simple proportionality factor between force and acceleration as in Newtonian mechanics. The different inertia in the direction of movement and transversely to it was initially attempted to be understood using the terms longitudinal and transversal mass, but these are no longer used today.
In this and other articles the size is no longer used, and the symbol for the mass always has the meaning of the rest mass, so it should be noted, however, that sometimes, especially in older texts, the symbol stands for the relativistic mass.
Resting energy
The rest energy is the energy of a body or system in its rest system d. H. in the frame of reference in which its total momentum is zero. The rest energy is a property of the system that does not depend on its state of motion. The famous Einstein equation follows from the energy-momentum relation given above:
This means that the rest energy is clearly determined by the mass of the system and vice versa. Both quantities differ only in the constant factor and are therefore equivalent, see equivalence of mass and energy .
The rest energy of particles has an effect in particular during creation (e.g. pair formation ) and annihilation processes (e.g. annihilation ). The rest energy of the electron is 0.511 MeV , that of a proton is 938 MeV. To speak of the rest energy of a photon is a contradiction in terms, because there is no reference system in which the photon has no momentum. Instead, the statement is correct for the photon .
Multi-particle systems
For a system of several non-interacting particles, the total energy and the total momentum are the sums of the respective sizes of all particles. The energy-momentum relation is therefore
where is the number of particles. Here the invariant mass of the multi-particle system is generally not equal to the sum of the masses of the individual particles. Multiplying the invariant mass by the constant factor results in the rest energy of the system, in this context also referred to as the center of gravity energy . This includes not only the rest energies of the individual particles, but also their relative movement in relation to the center of gravity. To explain this, imagine a vessel that contains a gas. If energy is added to the gas by compressing or heating it, the vessel as a whole has an increased center of gravity energy and thus a greater invariant mass. When viewed in detail, the mass of the individual gas molecules does not change, but their kinetic energy relative to the common center of gravity does.
The center of mass energy is - like the invariant mass - invariant under Lorentz transformation . It indicates the amount of energy that is available for the generation of new particles in the event of a particle collision, and is therefore of importance in experimental particle physics .
Mass defect
Does a closed system give energy beyond the system limits e.g. B. in the form of radiation, the energy content of the system and thus its mass is reduced. In this sense, mass is no longer a conserved quantity in modern physics, although this is hardly noticeable in everyday situations.
In nuclear reactions , however, amounts of energy are converted that can no longer be neglected compared to the resting energy of the core components. The binding energy means that an atomic nucleus has a weighably lower mass than the sum of its components. The difference is called the mass defect. The binding energy of most atomic nuclei is between 7 and 9 MeV per nucleon and thus causes a mass defect between 0.7 and 0.9 percent. Very light atomic nuclei ( 2 H, 3 H, 3 He, Li, Be, B) show lower binding energies per nucleon with 1 to 6 MeV and lower mass defects with 0.1 and 0.6 percent.
The binding energy of chemical bonds is typically 2 to 7 eV per bond (per nucleon it would be significantly smaller, depending on the molecular weight) by 7 to 9 orders of magnitude lower. Therefore, a chemical mass defect could not yet be detected by weighing. The values for some reactions are in the range of the detection limit of current mass comparators ( percent): The largest chemical mass defect is percent in the bond . To include a mass defect of percent.
Since the mass defect in chemical bonding is so small that it would not be noticeable when weighing, Antoine de Lavoisier was able to establish the law of conservation of mass at the end of the 18th century . This knowledge contributed significantly to the departure from alchemy and phlogiston theory and thus became an important basis for chemistry based on the concept of chemical elements .
general theory of relativity
In the general theory of relativity , the free fall of bodies in the gravitational field is understood as force-free. Any acting forces would cause the trajectories to deviate from free fall. If the body is prevented from free fall, a force is required whose size is proportional to the inertial mass of the body.
The world lines of freely falling particles are the straight lines (more precisely: geodesics ) of space-time . They are completely determined by the initial location and the initial speed and do not depend on other properties such as the size or mass of the freely falling particle ( principle of equivalence ). Since spacetime is curved, the projection of the geodesics onto the three-dimensional spatial space does not normally result in straight lines, but rather trajectory parabolas, for example.
In the basic equation of general relativity, the source of gravitation is the energy-momentum tensor, which is composed of energy density, momentum densities, energy flows and momentum flows. Since the energy of resting bodies is determined by their mass, only their mass causes gravitation. If one can neglect the movement of the bodies producing gravity and if the speed of the free falling particles is small compared to the speed of light, then the mass of the bodies producing gravity has an effect as in Newton's theory of gravity. This restriction does not apply to light as a test particle: it is deflected twice as much in the sun as would be expected according to Newton.
Origin of the masses of the elementary particles
In the standard model of elementary particle physics , the origin of the masses of elementary particles is explained by the Higgs mechanism . By interacting with the Higgs field , which is indirectly detected by observing the Higgs boson , they acquire a mass, since the Higgs field does not disappear even in a vacuum. Only the mass of the Higgs boson itself is not explained by this. In supersymmetric theories , a similar mechanism could also be mediated by other particles ( Goldstinos ) (see also Goldstonetheorem and Gravitino ).
The masses of the baryons , which also include protons and neutrons, are, however, about 100 times greater than the masses of the three quarks they are made of. The baryon masses are explained dynamically (see also: bound state ). Lattice calculations in quantum chromodynamics (QCD) provide approaches to the calculation . One can argue with the small extension of the baryons of about 10 −15 m in a semi-descriptive manner: If the quarks in the baryon concentrate in such a small space, they have such a short De Broglie wavelength that their kinetic energy, according to Einstein's formula, is considerable means. Three such constituent quarks then actually give about the mass of the proton or neutron.
The baryons make up most of the mass of visible matter. It is believed that weakly interacting massive particles (English weakly interacting massive particles , WIMP abbreviated), such as the hypothetical lightest supersymmetric particle (English lightest supersymmetric particle , abbreviated LSP) the invisible dark matter could build.
Usage: mass and weight
In common parlance, the mass of an object is also referred to as its weight. Examples are excess weight , empty weight , drained weight or weight information in cooking recipes. This also applies to many laws and regulations. Examples are the German Maternity Protection Act and the Swiss Road Traffic Act .
When equating mass and weight , the impression can arise that the mass depends on the local gravity. The following statement is misleading: “On the moon, a person weighing 60 kg weighs only about 10 kg.” More clear: “A person with a 'weight' on earth of 60 kg weighs about as much on the moon as one Person with a 'weight' of 10 kg on earth. "
See also
literature
- Max Jammer : The concept of mass in physics. Wissenschaftliche Buchgesellschaft, Darmstadt 1964 (Concepts of Mass in Classical and Modern Physics, Harvard 1961, German).
- Gordon Kane: The Secret of the Crowd . In: Spectrum of Science . No. 2 . Spectrum of Science Verlag, 2006, ISSN 0170-2971 , p. 36-43 .
Web links
- Page no longer available , search in web archives: PTB's page on the kilogram (with references to projects for redefinition)
- Trials and tasks to the mass ( LEIFI )
- Cornelius C. Noack: What actually is a 'rest mass'? (PDF; 279 kB).
- The Problem of Mass for Quarks and Leptons. Lecture by Harald Fritzsch on March 22, 2000 at the Kavli Institute for Theoretical Physics (lecture documents / audio recording).
- Lew Borissowitsch Okun : The Concept of Mass in the Einstein Year. (arXiv). PDF, 175 kB.
Individual evidence
- ^ Isaac Newton: Philosophiae Naturalis Principia Mathematica. Preface to the 3rd edition, explanations, German translation.
- ^ Lev B. Okun (2006): The Concept of Mass in the Einstein Year. Retrieved May 28, 2015.
- ↑ a b c d Hermann Weyl: What is matter? (Chapter 2.) . In: The natural sciences . tape 12 , no. 29 , 1924, pp. 585-593 .
- ^ Peter Mittelstaedt: Classical mechanics. BI Wissenschaftsverlag, Mannheim u. a. 1994.
- ↑ a b Cornelius C. Noack: What actually is a 'rest mass'? (PDF; 279 kB), accessed on May 28, 2015.
- ↑ Wikipedia adheres exclusively to the modern choice of words.
- ^ A b Lev B. Okun: The Concept of Mass. In: Physics Today. 43, 32 (1989). DOI: 10.1063 / 1.881171 PDF , accessed on December 22, 2016.
- ↑ In this quote means the same as . By “momentum” Einstein means the impulse of the body.
- ↑ In corresponding texts the letter is often used for the relativistic mass. In Wikipedia this is avoided whenever possible to avoid confusion.
- ↑ CERN experiments observe particle consistent with long-sought Higgs boson. In: Press release from CERN. July 4, 2012, accessed July 4, 2012 .
- ↑ DELPHI Collaboration: P. Abreu et al .: Search for the goldstino at √ s from 189 to 202 GeV . In: CERN-EP / 2000-110 . August 16, 2000 (English, PDF, online ).
- ↑ About § 11 Paragraph 5 No. 1 MuSchG: "Loads of more than five kilograms"
- ↑ For example Art. 9: “The maximum permissible weight for vehicles or vehicle combinations is 40 t”, cf. Text (PDF; 357 kB) of the Swiss Road Traffic Act.




































































![{\ displaystyle \ left [\ rho \ right] = 1 \, \ mathrm {\ frac {kg} {m ^ {3}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07e2731f54ed0f7f5198ed5733d556ac2e8ba2f2)


![{\ displaystyle \ left [M \ right] = 1 \, \ mathrm {\ frac {kg} {mol}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b07b9d91422c69f6cd618e4d9deea1962bc1ceeb)










































