Ramsey's theorem

The title of this article is ambiguous. For the theorem in set theory see Ramsey theorem (set theory) .

The set of Ramsey goes to Frank P. Ramsey back and its publication from the year 1930th It is one of the classic theorems of combinatorics and represents a generalization of the Dirichlet's drawer principle . The sentence deals with the question of whether and under what conditions single-colored subgraphs occur when edge coloring of complete graphs and hypergraphs with two (or more) colors . It follows that such subgraphs must always appear for sufficiently large complete graphs and hypergraphs. The branch of combinatorics dealing with such questions is called Ramsey theory .

In addition to the pure question of existence, a related quantification problem is also investigated in discrete mathematics. It is a question of the size from which a complete graph or hypergraph in the sense mentioned is to be regarded as “sufficiently large”, and also how the Ramsey numbers to be determined in this sense are to be calculated or at least estimated. Clarifying or even solving this question of quantification has turned out to be extremely difficult.

With Ramsey's theorem , existence theorems of discrete mathematics can be derived and, in particular, combinatorial problems of geometry and number theory can be solved. It can also be used in practice in the game Sim .

Statement of the theorem (version for complete graphs)

We consider finite complete graphs with vertices and edge colors, where each edge of is colored with one of two colors, say red and blue. If there are nodes here such that all edges running between these edges are red, then we say that the graph contains a red subgraph . A corresponding way of speaking applies to blue subgraphs . ${\displaystyle K_{n}}$ ${\displaystyle n}$ ${\displaystyle (n\in \mathbb {N} )}$ ${\displaystyle K_{n}}$ ${\displaystyle r}$ ${\displaystyle r}$

With this way of speaking, Ramsey's theorem (in the version for graphs) can be stated as follows:

For every two natural numbers there is always a natural number ( dependent on and ) such that every complete graph with nodes, the edges of which are either red or blue, contains at least one red subgraph or one blue subgraph. ${\displaystyle r,b}$ ${\displaystyle r}$ ${\displaystyle b}$ ${\displaystyle R}$ ${\displaystyle K_{n}}$ ${\displaystyle n\geq R}$ ${\displaystyle r}$ ${\displaystyle b}$

Ramsey numbers for complete graphs

The smallest natural number that can be chosen as such at a given is called the Ramsey number belonging to and and is denoted by. ${\displaystyle R}$ ${\displaystyle r,b}$ ${\displaystyle r}$ ${\displaystyle b}$ ${\displaystyle R(r,b)}$

A characteristic of the Ramsey number is the property that it is the largest complete graph which allows red-blue edge coloring for which neither a red subgraph nor a blue subgraph exists in. ${\displaystyle R(r,b)}$ ${\displaystyle K_{R(r,b)-1}}$ ${\displaystyle r}$ ${\displaystyle b}$ ${\displaystyle K_{R(r,b)-1}}$

The Ramsey's theorem for complete graphs can be of edge-colorings with two of those with unlimited colors generalize. Correspondingly, there is the corresponding Ramsey number for any edge coloring with colors     and numbers . ${\displaystyle t}$ ${\displaystyle (t\in \mathbb {N} )}$ ${\displaystyle q_{1},\ldots ,q_{t}}$ ${\displaystyle R(q_{1},\ldots ,q_{t})}$

Simple examples

• The general rule is how to recognize by swapping the colors. ${\displaystyle R(r,b)=R(b,r)}$
• ${\displaystyle R(r,1)=1}$: Every subgraph with only one corner is automatically monochrome.
• ${\displaystyle R(r,2)=r}$: Either all edges are red or there is a blue edge.

To calculate R (3.3)

A 2-staining of K ₅ without monochromatic K ₃

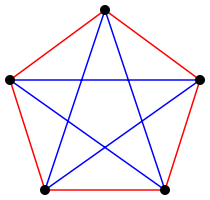
The picture on the right shows that it is possible to color the graph, i.e. the complete graph with five corners, with two colors, red and blue, so that neither a red nor a blue triangle appears. Consequently, the following certainly applies: or . ${\displaystyle K_{5}}$ ${\displaystyle R(3,3)>5}$ ${\displaystyle R(3,3)\geq 6}$

Conversely, if one looks at a corner that is red-blue colored in any way and here any corner , one of the two colors appears at the five edges ending in, oBdA . red, at least three times ( drawer principle ). If one of the edges between the three corresponding end points is red, we have a red one . Otherwise, all of the edges between these three endpoints are blue, and we have a blue one . So in every red-blue-colored one finds a red or a blue , i.e. . h, the following applies: . ${\displaystyle K_{6}}$ ${\displaystyle v}$ ${\displaystyle v}$ ${\displaystyle K_{3}}$ ${\displaystyle K_{3}}$ ${\displaystyle K_{6}}$ ${\displaystyle K_{3}}$ ${\displaystyle K_{3}}$ ${\displaystyle R(3,3)\leq 6}$

So overall you get . ${\displaystyle R(3,3)=6}$

Further identities, inequalities and values ​​for the Ramsey numbers for complete graphs

In general, the following relationships apply:

• ${\displaystyle R(r,b)=R(b,r)}$
• ${\displaystyle R(r,1)=R(1,r)=1}$   For   ${\displaystyle r\geq 1}$
• ${\displaystyle R(r,2)=R(2,r)=r}$   For   ${\displaystyle r\geq 1}$
• ${\displaystyle R(r_{1},b_{1})\leq R(r_{2},b_{2})}$   For   ${\displaystyle r_{1}\leq r_{2},b_{1}\leq b_{2},}$
• ${\displaystyle R(r,b)\leq R(r-1,b)+R(r,b-1)}$  For   ${\displaystyle r,b\geq 2}$
• ${\displaystyle R(r,b)\leq R(r-1,b)+R(r,b-1)-1}$   For   ${\displaystyle r,b\geq 3\,,\,R(r-1,b)\equiv R(r,b-1)\equiv 0{\pmod {2}}}$

From the penultimate inequality , one obtains the following derived inequality:

• ${\displaystyle R(r,b)\leq {\binom {r+b-2}{r-1}}}$   for    . ${\displaystyle r,b\geq 1}$

In the event this can be tightened: ${\displaystyle r=3}$

• ${\displaystyle R(3,b)\leq {\frac {1}{2}}(b^{2}+3)}$   for    . ${\displaystyle b\geq 3}$

For the general case   in which any edge coloring with two, three or more colors is permitted, the following applies: ${\displaystyle t=2,3,\ldots }$

• ${\displaystyle R(q_{1},q_{2},\ldots ,q_{t})\leq {\bigl (}R(q_{1}-1,q_{2},\ldots ,q_{t})+R(q_{1},q_{2}-1,\ldots ,q_{t})+\cdots +R(q_{1},q_{2},\ldots ,q_{t}-1){\bigr )}-t+2}$   for    . ${\displaystyle q_{1},\ldots ,q_{t}\geq 2}$

A rough limitation of these Ramsey numbers is given by the following inequalities, the derivation of which was essentially based on probabilistic methods :

• ${\displaystyle 2^{r/2}<R(r,r)<4^{r-1}}$   for    . ${\displaystyle r\geq 3}$

The exact values ​​for these Ramsey numbers for edge coloring with two colors are - apart from the simple examples - only known for smaller graphs. There are:

• ${\displaystyle R(3,3)=6}$
• ${\displaystyle R(3,4)=9}$
• ${\displaystyle R(3,5)=14}$
• ${\displaystyle R(3,6)=18}$
• ${\displaystyle R(3,7)=23}$
• ${\displaystyle R(3,8)=28}$
• ${\displaystyle R(3,9)=36}$

such as

• ${\displaystyle R(4,4)=18}$
• ${\displaystyle R(4,5)=25}$  .

After that, only estimates such as

• ${\displaystyle 35\leq R(4,6)\leq 41}$

or

• ${\displaystyle 43\leq R(5,5)\leq 48}$  .

Exact numbers about the Ramsey numbers for edge coloring with three or more colors are only available in very small quantities. Not much more is known here than

• ${\displaystyle R(3,3,3)=17}$

and then an upper and lower limit for edge coloring with four colors:

• ${\displaystyle 51\leq R(3,3,3,3)\leq 65}$  .

illustration

To illustrate the meaning of a Ramsey number , it is helpful to relate it to the answer to the following question: ${\displaystyle R(r,b)}$

• How many people have to appear at a party, at least if you want to be guaranteed that either of them (or more) do not know each other or (or more) to know each other . ${\displaystyle r}$ ${\displaystyle b}$

If one sets the relation of knowing one another , understood in the sense of a two-sided acquaintance with one another , equal to an irreflexive , symmetrical (but not necessarily transitive ) relation , one arrives at a graph with red and blue edges, in that case that any two guests do not know each other draws a red line, but in the opposite case, if they know each other, draws a blue line.

This makes it very easy to determine the Ramsey number, for example . So here is and . ${\displaystyle R(3,2)=3}$ ${\displaystyle r=3}$ ${\displaystyle b=2}$

If we then have any three guests, we can draw the complete graph and achieve the following possible edge coloring: ${\displaystyle K_{3}}$

• All edges are colored red.
• All edges are colored blue.
• Two edges are colored blue and one red.
• Two edges are colored red and one blue.

For the three guests this means:

• None of the guests knows another.
• All three guests know each other.
• One guest knows the other two guests, but they don't know each other.
• Two guests know each other, but are not acquainted with the third guest.

Overall, this means for the determination of  : ${\displaystyle R(3,2)=3}$

For a party at which at least three of the guests who appear do not know each other or at least two do not know each other, it is sufficient if three or more guests appear.

Ramsey's general theorem (finite version for uniform hypergraphs)

In the version of Ramsey's theorem for graphs, the two colors red and blue were given. A red-blue edge coloring of a graph is, according to its mathematical meaning, a mapping of the set of edges of the graph into the set . In place of the quantity , any other two can be elements existing amount for labeling the edges and select the particular quantity . Instead of the red-blue edge coloring, the edges are marked with the numbers and . In this way it becomes clear that red-blue edge coloring is tantamount to classifying the edges into two classes. ${\displaystyle \{{rot},{blau}\}\,}$ ${\displaystyle 2}$ ${\displaystyle \{{rot},{blau}\}\,}$ ${\displaystyle 2}$ ${\displaystyle \{1,2\}\subset \mathbb {N} \,}$ ${\displaystyle 1}$ ${\displaystyle 2}$

This approach can be generalized in several ways. Instead of two classes, finitely many classes are considered in any finite number (i.e. pieces), instead of the edges (which are nothing more than -element subsets of the node set of graphs) any -subset (with ) of any finite set and instead of the two numbers any natural numbers presented . ${\displaystyle t=1,2,3,\ldots }$ ${\displaystyle 2}$ ${\displaystyle k}$ ${\displaystyle k=1,2,3,\ldots }$ ${\displaystyle X\,}$ ${\displaystyle r,b\,}$ ${\displaystyle q_{1},q_{2},\ldots ,q_{t}\,}$

This leads to Ramsey's general theorem , which holds for the case of the complete ( k-uniform ) hypergraph:

For every natural number   and     any given natural number with there is always a natural number dependent on with the following property: ${\displaystyle t}$ ${\displaystyle t+1}$ ${\displaystyle k,q_{1},q_{2},\ldots ,q_{t}}$ ${\displaystyle k\leq \min(q_{1},q_{2},\ldots ,q_{t})}$ ${\displaystyle k,q_{1},q_{2},\ldots ,q_{t}}$ ${\displaystyle R}$

Is a natural number with and an elementary set and is some fraction ${\displaystyle n\,}$ ${\displaystyle n\geq R}$ ${\displaystyle X}$ ${\displaystyle n}$

${\displaystyle {X \choose k}={\mathcal {K}}_{1}{\dot {\cup }}{\mathcal {K}}_{2}{\dot {\cup }}\,\dots {\dot {\cup }}{\mathcal {K}}_{t}\,}$

the set system of all subsets of     in     classes before, ${\displaystyle k}$ ${\displaystyle X}$ ${\displaystyle t}$

so there is always at least one index and a subset     such that the conditions: ${\displaystyle s\in \{1,2,\ldots ,t\}\,}$ ${\displaystyle T\subseteq X\,}$

${\displaystyle |T|=q_{s}\,}$

and

${\displaystyle {T \choose k}\subseteq {\mathcal {K}}_{s}\,}$

are fulfilled.

Higher (classical) Ramsey numbers for uniform hypergraphs

The smallest natural number that   can be chosen as a number     in the general theorem of Ramsey given     and given   is called the   Ramsey number belonging to     and   or similar. Such a number is also called a higher (classical) Ramsey number ( English k-hypergraph Ramsey number or also classical hypergraph Ramsey number ). It is often referred to as     or in a similar way. ${\displaystyle R}$ ${\displaystyle k}$ ${\displaystyle q_{1},q_{2},\ldots ,q_{t}}$ ${\displaystyle k\,}$ ${\displaystyle q_{1},q_{2},\ldots ,q_{t}}$ ${\displaystyle R(q_{1},q_{2},\ldots ,q_{t};k)}$

Identities, inequalities and values ​​to the higher Ramsey numbers

With the designations mentioned in the sentence above, the following identities apply :

• ${\displaystyle R(q_{1},q_{2};2)=R(q_{1},q_{2})}$   such as   ${\displaystyle R(q_{1},\ldots ,q_{t})=R(q_{1},\ldots ,q_{t};2)}$
• ${\displaystyle R(2,2,\ldots ,2;2)=2}$
• ${\displaystyle R(q_{1},q_{2},\ldots ,q_{t};1)=q_{1}+q_{2}+\cdots +q_{t}-t+1}$
• ${\displaystyle R(q_{1},k,\ldots ,k;k)=q_{1}}$   For ${\displaystyle k,q_{1}\in \mathbb {N} \,,\,q_{1}\geq k}$

The   following inequality is also given for the case   : ${\displaystyle t=2}$

• ${\displaystyle R(q_{1},q_{2};k)\leq 1+R{\bigl (}{R(q_{1}-1,q_{2};k),R(q_{1},q_{2}-1;k);k-1}{\bigr )}}$   For ${\displaystyle q_{1},q_{2},k\in \mathbb {N} \,,\,1<k<\min(q_{1},q_{2})}$

In addition, for the case     and     : ${\displaystyle t=2,3,\ldots }$ ${\displaystyle k=2}$

• ${\displaystyle R(q_{1},q_{2},\ldots ,q_{t};2)\leq {\bigl (}R(q_{1}-1,q_{2},\ldots ,q_{t};2)+R(q_{1},q_{2}-1,\ldots ,q_{t};2)+\cdots +R(q_{1},q_{2},\ldots ,q_{t}-1;2){\bigr )}-t+2}$   for    . ${\displaystyle q_{1},\ldots ,q_{t}\geq 2}$

For   and   there is the following tightening: ${\displaystyle t=2}$ ${\displaystyle q_{1}=3}$

• ${\displaystyle R(3,q_{2};2)\leq {\frac {1}{2}}({q_{2}}^{2}+3)}$   for    . ${\displaystyle q_{2}\geq 3}$

Exact values ​​for the higher Ramsey numbers are, as far as one disregards the simple examples given and the above values ​​of the Ramsey numbers for small graphs, largely unknown. The Ramsey number for is an exception     . The following applies here: ${\displaystyle t=2,k=3,q_{1}=q_{2}=4}$

• ${\displaystyle R(4,4;3)=13}$   .

The infinite version of Ramsey's theorem

The infinite version of Ramsey's theorem is the one that essentially corresponds to the theorem originally proposed by Frank Plumpton Ramsey in 1930 . It is:

To any given natural numbers , to any given infinite set and any decomposition ${\displaystyle k,t\,}$ ${\displaystyle X}$

${\displaystyle {X \choose k}={\mathcal {K}}_{1}{\dot {\cup }}{\mathcal {K}}_{2}{\dot {\cup }}\,\dots {\dot {\cup }}{\mathcal {K}}_{t}\,}$

of the set system of all -subset of ${\displaystyle k}$ ${\displaystyle X\,}$

there is always at least one index and an infinite subset with ${\displaystyle s\in \{1,2,\ldots ,t\}\,}$ ${\displaystyle T\subseteq X\,}$

${\displaystyle {T \choose k}\subseteq {\mathcal {K}}_{s}\,}$   .

It can be shown that the infinite version of Ramsey's theorem leads to the finite version.

Inferences

This Ramsey theorem has remarkable consequences, for example in geometry and in number theory . Among other things, it gives rise to the famous Happy Ending theorem by Erdős and Szekeres from 1935 and an expanded version of Schur's theorem .

Happy ending theorem

For any given natural number   there is always a natural number   that is solely     dependent on     and has the property that the more     or more points of the Euclidean plane that are in a general position always contain a convex polygon with   corner points . ${\displaystyle m\geq 3}$ ${\displaystyle m\,}$ ${\displaystyle \kappa }$ ${\displaystyle \kappa }$ ${\displaystyle m}$  

According to Halder and Heise, this sentence can be expressed even more sharply:

For any given natural number     there is always a natural number     with the property that each     or more points of the Euclidean plane   contain at least   collinear points or a convex polygon with   corner points. ${\displaystyle m\geq 3}$ ${\displaystyle \kappa }$ ${\displaystyle \kappa }$ ${\displaystyle m}$   ${\displaystyle m}$

If one denotes the smallest natural number, which satisfies   the happy ending theorem for a given natural number   (in the first slightly weaker version)     , then one has the     following exact value: ${\displaystyle m\geq 3}$ ${\displaystyle \kappa (m)}$ ${\displaystyle m=3,4,5,6}$

• ${\displaystyle \kappa (m)=2^{m-2}+1}$   .

So there are

• ${\displaystyle \kappa (3)=3}$
• ${\displaystyle \kappa (4)=5}$
• ${\displaystyle \kappa (5)=9}$
• ${\displaystyle \kappa (6)=17}$   .

Beyond that, no further exact values ​​are known, only a general range of values :

• ${\displaystyle 2^{m-2}+1\leq \kappa (m)\leq {\binom {2m-5}{m-2}}+2}$   for everyone   . ${\displaystyle m\geq 3}$

Schur's theorem (extended version)

For every two arbitrarily given natural numbers     with     there is always a smallest natural number     with the following property: ${\displaystyle m,t}$ ${\displaystyle m\geq 2}$ ${\displaystyle S=S(m,t)}$

Is     a natural number with     and there is   some decomposition for the starting part ${\displaystyle n}$ ${\displaystyle n\geq S}$   ${\displaystyle A=\{1,2\,\ldots ,n\}\subset \mathbb {N} }$

${\displaystyle A=A_{1}{\dot {\cup }}A_{2}{\dot {\cup }}\,\dots {\dot {\cup }}A_{t}\,}$

in     classes before, ${\displaystyle t}$

so at least one of the sets contains   a   - tuple   of (not necessarily different) numbers which give the equation: ${\displaystyle A_{s}\,(s\in \{1,2,\ldots ,t\})}$ ${\displaystyle m}$   ${\displaystyle (a_{1},a_{2}\,\dots ,a_{m})}$

${\displaystyle a_{1}+a_{2}+\,\dots +a_{m-1}=a_{m}}$

fulfill.

additive

The proof given by Halder and Heise shows that the Schur number   defined by Schur's theorem is   always below the Ramsey number     . ${\displaystyle S(m,t)}$ ${\displaystyle R(q_{1},q_{2},\ldots ,q_{t};2)}$   ${\displaystyle (q_{1}=q_{2}=\,\ldots =q_{t}=m)}$

Generalization of Ramsey's theorem for finite simple graphs

In the case of graphs (see Part 1), Ramsey's theorem deals with the question of whether and how sufficiently large complete graphs can be found so that     at least one of the   given complete graphs can be embedded as a monochrome subgraph with every edge coloring   . ${\displaystyle K_{n}}$ ${\displaystyle K_{n}}$ ${\displaystyle t}$ ${\displaystyle K_{q_{i}}}$

This concept has been generalized in such a way that one now moves from the     to arbitrary simple graphs of     finite order . In this way the following generalization of Ramsey's theorem for graphs is obtained : ${\displaystyle K_{q_{i}}}$ ${\displaystyle {\mathcal {G}}_{i}}$

For every natural number     and any given family     of finite simple graphs there is always a natural number     with the following property: ${\displaystyle t\geq 2}$ ${\displaystyle t}$ ${\displaystyle ({\mathcal {G}}_{1},{\mathcal {G}}_{2},\ldots ,{\mathcal {G}}_{t})}$ ${\displaystyle r}$

If   and     and if there   is any edge coloring of     with     colors, then there is a monochrome subgraph which contains the isomorphic image of at least one of the graphs   . ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle n\geq r}$ ${\displaystyle K_{n}}$ ${\displaystyle t}$ ${\displaystyle K_{n}}$ ${\displaystyle {\mathcal {G}}_{1},{\mathcal {G}}_{2},\ldots ,{\mathcal {G}}_{t}}$

Generalized Ramsey numbers for finite simple graphs

The smallest natural number that can be chosen as a number     in the generalization of Ramsey's theorem for graphs given is called the   corresponding (generalized) Ramsey number (or similar) and is     denoted by. ${\displaystyle r}$ ${\displaystyle {\mathcal {G}}_{1},{\mathcal {G}}_{2},\ldots ,{\mathcal {G}}_{t}}$ ${\displaystyle {\mathcal {G}}_{1},{\mathcal {G}}_{2},\ldots ,{\mathcal {G}}_{t}}$ ${\displaystyle r({\mathcal {G}}_{1},{\mathcal {G}}_{2},\ldots ,{\mathcal {G}}_{t})}$

The following general relationships apply to them:

• ${\displaystyle r(K_{q_{1}},K_{q_{2}},\ldots ,K_{q_{t}})=R(q_{1},q_{2},\ldots ,q_{t})=R(q_{1},q_{2},\ldots ,q_{t};2)}$
• ${\displaystyle r({\mathcal {G}}_{1},{\mathcal {G}}_{2},\ldots ,{\mathcal {G}}_{t})\leq R(q_{1},q_{2},\ldots ,q_{t};2)}$   , if   ${\displaystyle n({\mathcal {G}}_{i})=q_{i}}$   ${\displaystyle (i=1,2,\ldots ,t)}$
• ${\displaystyle r({\mathcal {G}}_{\sigma (1)},{\mathcal {G}}_{\sigma (2)},\ldots ,{\mathcal {G}}_{\sigma (t)})=r({\mathcal {G}}_{1},{\mathcal {G}}_{2},\ldots ,{\mathcal {G}}_{t})}$   for each permutation   ${\displaystyle \sigma \colon \{1,2,\ldots ,t\}\rightarrow \{1,2,\ldots ,t\}}$

As with the above Ramsey numbers, concrete results are known for the generalized Ramsey numbers for simple graphs in only a few cases. These include the following:

• ${\displaystyle r(C_{3},C_{3})=6}$
• ${\displaystyle r(C_{4},C_{4})=6}$
• ${\displaystyle r(C_{5},C_{5},C_{5})=17}$
• ${\displaystyle r(C_{7},C_{7},C_{7})=25}$
• ${\displaystyle r(B_{q_{1}},K_{q_{2}})=1+(q_{1}-1)(q_{2}-1)}$   for     ,     and tree graphs   with   ${\displaystyle q_{1},q_{2}\in \mathbb {N} }$ ${\displaystyle q_{1}\geq 2}$   ${\displaystyle B_{q_{1}}}$ ${\displaystyle n(B_{q_{1}})=q_{1}}$
• ${\displaystyle r(K_{1,q_{1}},K_{1,q_{2}},\ldots ,K_{1,q_{t}})=\alpha -t+q_{1}+q_{2}+\cdots +q_{t}}$   for   star graphs   , where     is if there are   two or more even numbers among the natural numbers   and their number is an even number, and     otherwise ${\displaystyle t\geq 2}$     ${\displaystyle K_{1,q_{i}}}$   ${\displaystyle (i=1,2,\ldots ,t)}$ ${\displaystyle \alpha =1}$ ${\displaystyle q_{1},q_{2},\ldots ,q_{t}}$ ${\displaystyle \alpha =2}$

Asymptotic estimates

Although the classical Ramsey numbers as well as the generalized Ramsey numbers for graphs are only determined exactly in a few cases, they can be given certain asymptotic estimates. The following result, which is based in particular on the work of Miklós Ajtai , János Komlós and Endre Szemerédi (1980) and Jeong Han Kim (1995), is often mentioned:

• There are two real constants     with ${\displaystyle C_{1},C_{2}>0}$

  ${\displaystyle {C_{1}\cdot {\frac {n^{2}}{\ln(n)}}}\leq R(3,n;2)\leq {C_{2}\cdot {\frac {n^{2}}{\ln(n)}}}}$     ${\displaystyle (n\in \mathbb {N} \,,\,n\geq 2)}$   .

assumptions

There are a number of conjectures about the classical Ramsey numbers as well as the generalized Ramsey numbers for graphs. These are often associated with the name and person of Paul Erdős . These include the following:

Conjecture from Erdős

Paul Erdős made the following conjecture in 1973, which connects the Ramsey numbers, the generalized Ramsey numbers for graphs and their chromatic numbers :

• If a finite simple graph has     the chromatic number     , then we have     . ${\displaystyle {\mathcal {G}}}$ ${\displaystyle \chi ({\mathcal {G}})=n}$     ${\displaystyle (n\in \mathbb {N} )}$ ${\displaystyle r({\mathcal {G}},{\mathcal {G}})\geq R(n,n)}$

Conjecture by Bondy and Erdős

In 1973, John Adrian Bondy and Paul Erdős made the following conjecture by Bondy and Erdős about the Ramsey numbers for circular graphs:

• It always   applies to circular graphs     , provided     and is odd   . ${\displaystyle C_{n}}$ ${\displaystyle n\geq 5}$ ${\displaystyle r(C_{n},C_{n},C_{n})=4n-3}$

So far secured is that for such odd numbers     always the inequality ${\displaystyle n}$

• ${\displaystyle r(C_{n},C_{n},C_{n})\geq 4n-3}$

Endures.

Tree guess

Stefan A. Burr and Paul Erdős expressed in 1976, the so-called tree-guess ( english Tree Conjecture ):

• For tree graphs     and     with     is always     . ${\displaystyle B_{p}}$ ${\displaystyle B_{q}}$ ${\displaystyle p,q\geq 2}$ ${\displaystyle r(B_{p},B_{q})\leq p+q-2}$

Erdős-Sós conjecture

The Erdős-Sós-Conjecture , which Paul Erdős and Vera Turán Sós put forward in 1963, is linked to and goes further than the tree conjecture - as it implies it:

• In every finite simple graph     with     nodes and     (or more) edges there     is   always an isomorphic image of any tree graph     with   nodes as a subgraph. ${\displaystyle {\mathcal {G}}}$ ${\displaystyle n}$ ${\displaystyle 1+{\frac {n(p-2)}{2}}}$ ${\displaystyle (n,p\in \mathbb {N} \,\,,p\geq 2)}$ ${\displaystyle B_{p}}$ ${\displaystyle p}$

McKay and Radziszowski's conjecture

The conjecture by McKay and Radziszowski from 1997 states:

• ${\displaystyle r(5,5)=43}$

See also

• Ramsey theorem (set theory)

literature

Original work

• Miklós Ajtai , János Komlós , Endre Szemerédi : A note on Ramsey numbers . In: J. Combin. Theory Ser. A . tape 29 , 1980, pp. 354-360 ( ac.els-cdn.com [PDF]). MR0600598
• Stefan A. Burr , John A. Roberts : On Ramsey numbers for stars . In: Utilitas Math . tape 4 , 1973, p. 217-220 ( onlinelibrary.wiley.com [PDF]). MR0465920
• V. Chvátal: Tree-complete graph Ramsey numbers . In: J. Graph Theory . tape 1 , 1977, pp. 93 ( onlinelibrary.wiley.com [PDF]). MR0465920
• Václav Chvátal, Frank Harary : Generalized Ramsey theory for graphs. III. Small off-diagonal numbers . In: Pacific J. Math . tape 41 , 1972, p. 335-345 ( projecteuclid.org [PDF]). MR0314696
• EJ Cockayne : Color classes for r-graphs . In: Canad. Math. Bull . tape 15 , 1972, p. 349-354 . MR0340076
• Paul Erdős, George Szekeres: A combinatorial problem in geometry . In: Compositio Mathematica . tape 2 , 1935, p. 463-470 .
• Paul Erdős: Some remarks on the theory of graphs . In: Amer. Math. Soc . tape 2 , 1947, p. 292-294 ( ams.org [PDF]).
• Robert E. Greenwood , Andrew M. Gleason : Combinatorial relations and chromatic graphs . In: Canad. J. Math . tape 7 , 1955, pp. 1-7 ( cms.math.ca [PDF]). MR0067467
• Jeong Han Kim : The Ramsey number R (3, t) has order of magnitude t ^ 2 / log t . In: Random Structures Algorithms . tape 7 , 1995, p. 173-207 ( onlinelibrary.wiley.com [PDF]). MR1369063
• Brendan D. McKay , Stanisław P. Radziszowski : The first classical Ramsey number for hypergraphs is computed. In: Proceedings of the Second Annual ACM-SIAM Symposium on Discrete Algorithms (San Francisco, CA, 1991) . ACM, New York 1991, pp. 304-308 .
• FP Ramsey : On a problem of formal logic . In: Proc. London Math. Soc. (series 2) . tape 30 , 1930, p. 264-286 .
• G. Tóth , P. Valtr : Note on the Erdős – Szekeres theorem . In: Discrete Comput. Geom. Band 19 , 1998, pp. 457-459 . MR1615130

Monographs

• Béla Bollobás : Modern Graph Theory (=  Graduate Texts in Mathematics . Volume 184 ). 3. Edition. Springer, New York (et al.) 1998, ISBN 0-387-98488-7 ( MR1633290 ).
• JA Bondy , USR Murty: Graph Theory with Applications . MacMillan, London 1976, ISBN 0-333-17791-6 ( MR0411988 ).
• JA Bondy, USR Murty: Graph Theory (=  Graduate Texts in Mathematics . Volume 244 ). Springer Verlag, New York 1976, ISBN 978-1-84628-969-9 ( MR2368647 ).
• Ronald L. Graham , Bruce L. Rothschild , Joel H. Spencer : Ramsey Theory . John Wiley & Sons, New York 1980, ISBN 0-471-05997-8 .
• Heinz-Richard Halder , Werner Heise : Introduction to combinatorics . Hanser Verlag, Munich (among others) 1976, ISBN 3-446-12140-4 ( Google Books ).
• Egbert Harzheim : Ordered Sets (=  Advances in Mathematics . Volume 7 ). Springer Verlag, New York, NY 2005, ISBN 0-387-24219-8 ( MR2127991 ).
• Konrad Jacobs , Dieter Jungnickel : Introduction to combinatorics (=  de Gruyter textbook ). 2nd, completely revised and expanded edition. de Gruyter, Berlin (ua) 2004, ISBN 3-11-016727-1 .
• Stasys Jukna : Extremal Combinatorics (=  Texts in Theoretical Computer Science ). 2nd Edition. Springer Verlag, Heidelberg (ua) 2011, ISBN 978-3-642-17363-9 ( MR2865719 ).
• Jörg Neunhäuserer : Nice sentences in mathematics. An overview with short proofs (=  Springer textbook ). Springer Spectrum, Berlin, Heidelberg 2015, ISBN 978-3-642-54689-1 .
• Lutz Volkmann : Foundations of the graph theory . Springer Spectrum, Vienna, New York 1996, ISBN 3-211-82774-9 .

Manuals

• Jonathan L. Gross , Jay Yellen (Eds.): Handbook of Graph Theory (=  Discrete Mathematics and its Applications ). CRC Press, Boca Raton (et al.) 2004, ISBN 1-58488-090-2 .
• Kenneth H. Rosen (Ed.): Handbook of Discrete and Combinatorial Mathematics (=  Discrete Mathematics and its Applications ). CRC Press, 2000, ISBN 0-8493-0149-1 .

Web links

• Ramsey @ Home is a “ BOINC ” project that tries to find new lower bounds for Ramsey numbers through distributed computing .
• Ramsey theory
• Radziszowski's survey of small Ramsey numbers (PDF; 109 kB, English)
• Survey of directed-graph Ramsey numbers (English)

References and footnotes

1. ↑ The choice of colors is immaterial.
2. ↑ Handbook of Discrete and Combinatorial Mathematics . S. 150 ff .
3. ↑ The above considerations for the determination of R (3,3) already indicate some of the essential ideas which lead to the recursive estimation of the Ramsey numbers mentioned and then also to a proof of the theorem. However, this estimate is by far not sufficient for an exact determination of the Ramsey numbers.
4. ↑ The inequalities go back to the classic work by Paul Erdős and George Szekeres from 1935, with which the two authors were the first to link Ramsey's theorem with questions of graph theory and geometry . (Cf. 1) Erdős-Szekeres: A combinatorial problem in geometry . In: Proc. London Math. Soc. 1935, p. 463 ff . 2) Graham-Rothschild-Spencer: p. 24 ff. 3) Handbook of Graph Theory . S. 838 ff .
5. ↑ Volkmann: p. 359.
6. ↑ According to Lutz Volkmann, this inequality goes back to a paper by EJ Cockayne from 1972. See Volkmann: p. 363.
7. ↑ Erdős: Some remarks on the theory of graphs. In: Bull. Amer. Math. Soc. 1947, p. 292 ff .
8. ↑ Graham-Rothschild-Spencer: p. 75.
9. ↑ Handbook of Discrete and Combinatorial Mathematics . S. 151, 592 ff .
10. ↑ Handbook of Graph Theory . S. 840 .
11. ↑ The lower bound of results from the fact that a complete two-colored graph with nodes was found which does not contain a complete monochrome subgraph with nodes. See Neunhäuserer: pp. 31–32, 182–183. Further current estimates of edge coloring with two colors can be found in the article Ramsey's theorem of the English language Wikipedia. ${\displaystyle R(5,5)}$ ${\displaystyle 42}$ ${\displaystyle 5}$
12. ^ Greenwood-Gleason: Combinatorial relations and chromatic graphs . In: Canad. J. Math . 1955, p. 1 ff .
13. ↑ Bondy-Murty: p. 249.
14. ^ Jacobs-Jungnickel: p. 105.
15. ↑ Halder-Heise: pp. 141–142.
16. ↑ Harzheim: pp. 299-301.
17. ↑ ^{a b} Handbook of Discrete and Combinatorial Mathematics . S. 150 .
18. ^ Graham-Rothschild-Spencer: p. 90.
19. ↑ There are some designations. In particular, the choice of the descriptive letter is not uniform and at the same time the position of the     in relation to the can     change. Instead of the capital letter     one often finds the lower case letter     , especially in graph theory. Here, for example, the number     also appears as an index. In this sense (see Handbook of Graph Theory ): ${\displaystyle k}$ ${\displaystyle q_{i}}$ ${\displaystyle R}$ ${\displaystyle r}$ ${\displaystyle k}$
    • ${\displaystyle r(q_{1},q_{2})={r_{2}}(q_{1},q_{2})=R(q_{1},q_{2})=R(q_{1},q_{2};2)}$
    • ${\displaystyle r(q_{1},q_{2},\ldots ,q_{t})={r_{2}}(q_{1},q_{2},\ldots ,q_{t})=R(q_{1},q_{2},\ldots ,q_{t})=R(q_{1},q_{2},\ldots ,q_{t};2)}$
    • ${\displaystyle {r_{k}}(q_{1},q_{2},\ldots ,q_{t})=R(q_{1},q_{2},\ldots ,q_{t};k)}$   .
    Some authors - at least those of the older literature, such as Halder-Heise - even use the Greek lowercase letter as a function identifier     and there are other designations. The term used here essentially follows the general term (which is not solely based on graph theory) in Jacobs-Jungnickel or that of the Handbook of Discrete and Combinatorial Mathematics . ${\displaystyle \rho }$
20. ↑ Handbook of Graph Theory . S. 853 .
21. ^ Jacobs-Jungnickel: p. 108.
22. ↑ McKay Radziszowski: The first classical Ramsey number for hyper graphs is computed. In: Proceedings of the Second Annual ACM-SIAM Symposium on Discrete Algorithms . 1991, p. 304 ff .
23. ↑ This establishes the connection between general Ramsey numbers and Ramsey numbers for graphs.
24. ↑ Halder-Heise: p. 138.
25. ↑ The last two inequalities are taken from above.
26. ^ Jacobs-Jungnickel: pp. 109–110.
27. ^ Jacobs-Jungnickel: p. 110.
28. ↑ Jacobs-Jungnickel: pp. 108-109.
29. ↑ See also in the English-language WIKIPEDIA under: Happy Ending problem !
30. ↑ Halder-Heise: pp. 142–143.
31. ↑ Halder-Heise: pp. 140–141.
32. ↑ Handbook of Discrete and Combinatorial Mathematics . S. 832 .
33. ^ Tóth-Valtr: Note on the Erdős – Szekeres theorem . In: Discrete Comput. Geom. Band 19 , 1998, pp. 457 ff .
34. ↑ Halder-Heise: p. 143.
35. ↑ ^{a b} Volkmann: p. 362 ff.
36. ↑ Handbook of Discrete and Combinatorial Mathematics . S. 592 ff .
37. ↑ Handbook of Graph Theory . S. 838 ff .
38. ↑ This designation with the lower case letter instead of the upper case letter corresponds to the usual convention of graph theory (see earlier footnote) and is therefore used at this point. ${\displaystyle r}$ ${\displaystyle R}$
39. ↑ Handbook of Graph Theory . S. 842 ff .
40. ↑ This equation establishes the connection to the classical Ramsey numbers for complete graphs and at the same time proves that the generalized Ramsey numbers for finite simple graphs are in fact a generalization.
41. ↑ For   a graph   , one denotes     its order , i.e. the number of its nodes. ${\displaystyle n({\mathcal {G}})}$ ${\displaystyle {\mathcal {G}}}$
42. ↑   is the circle graph with     nodes and     edges. ${\displaystyle C_{n}}$ ${\displaystyle n}$ ${\displaystyle n}$
43. ↑ Chvátal: Tree-complete graph Ramsey numbers. In: J. Graph Theory . tape 1 , 1977, pp. 93 .
44. ^ Burr-Roberts: On Ramsey numbers for stars . In: Utilitas Math . tape 4 , 1973, p. 217 ff .
45. ↑ Jukna: p. 67.
46. ↑ Handbook of Graph Theory . S. 841 ff .
47. ↑ Further estimates of this kind can be found in the article on the English language Wikipedia. See here !
48. ^ Bondy-Murty: Graph Theory with Applications . S. 250 .
49. ↑ At the moment (as of December 2014) it cannot be said with absolute certainty whether Erdős' assumption is always open. In their expanded monograph Graph Theory from 2008, Bondy and Murty no longer included this assumption in the list of unsolved problems (p. 583 ff).
50. ↑ ^{a b} Handbook of Graph Theory . S. 843 .
51. ↑ Handbook of Graph Theory . S. 842 .
52. ↑ Bollobás: p. 135.
53. ↑ Neunhäuserer: pp. 182-183.