Laplace distribution

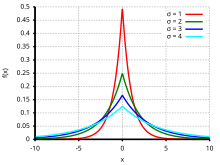
Density functions of the Laplace distribution for different parameters

The Laplace distribution (named after Pierre-Simon Laplace , a French mathematician and astronomer) is a continuous probability distribution . Since it has the form of two exponential distributions joined together , it is also known as the double exponential distribution or two-sided exponential distribution .

definition

A continuous random variable is subject to the Laplace distribution with the location parameter and the scale parameter if it has the probability density ${\displaystyle X}$ ${\displaystyle \mu \in \mathbb {R} }$ ${\displaystyle \sigma >0}$

${\displaystyle f(x)={\frac {1}{2\sigma }}e^{\displaystyle -{\frac {\left|x-\mu \right|}{\sigma }}}}$

owns.

Its distribution function is

${\displaystyle F(x)={\begin{cases}\displaystyle {1 \over 2}e^{\displaystyle {\frac {x-\mu }{\sigma }}},&x\leq \mu \\\displaystyle 1-{1 \over 2}e^{\displaystyle -{\frac {x-\mu }{\sigma }}}&x>\mu \end{cases}}}$

Using the Signum function , it can be displayed as closed

${\displaystyle F(x)={\tfrac {1}{2}}+{\tfrac {1}{2}}\operatorname {sgn} \left(x-\mu \right)\left(1-\exp \left(-{\frac {\left|x-\mu \right|}{\sigma }}\right)\right)}$.

properties

symmetry

The probability density is axisymmetric to the straight line and the distribution function is point-symmetric to the point . ${\displaystyle x=\mu }$ ${\displaystyle (\mu ,1/2)}$

Expected value, median, mode value

The parameter is expected value , median and mode value at the same time . ${\displaystyle \mu }$

${\displaystyle \operatorname {E} (X)=\mu }$

Variance

The variance is determined by the parameter . ${\displaystyle \sigma }$

${\displaystyle \operatorname {Var} (X)=2\sigma ^{2}}$

Crookedness

The skewness of the Laplace distribution is

${\displaystyle \operatorname {v} (X)=0}$.

Kurtosis

The curvature of a Laplace distribution is identical to 6 (corresponds to an excess of 3).

${\displaystyle \operatorname {Kurt} (X)=6}$

Accumulators

All cumulants with an odd degree are zero. For straight applies ${\displaystyle \kappa _{k}}$ ${\displaystyle k>2}$ ${\displaystyle k}$

${\displaystyle \kappa _{k}=2(k-1)!\sigma ^{k}}$

Moment generating function

The moment-generating function is a Laplace-distributed random variable with parameters and is ${\displaystyle \mu }$ ${\displaystyle \sigma }$

${\displaystyle M_{X}(t)={\frac {e^{\mu t}}{1-\sigma ^{2}t^{2}}}}$, For ${\displaystyle |t|<1/\sigma .}$

Characteristic function

The characteristic function arises from the moment-generating function by replacing the argument with , one obtains: ${\displaystyle t}$ ${\displaystyle is}$

${\displaystyle \phi _{X}(s)={\frac {e^{i\mu s}}{1+\sigma ^{2}s^{2}}}}$.

entropy

The entropy of the Laplace distribution (expressed in nats ) is

${\displaystyle 1+\ln(2\sigma )}$.

Random numbers

The inversion method is suitable for generating random numbers with double exponential distribution .

The pseudo inverse of the distribution function to be formed according to the simulation lemma reads here

${\displaystyle F^{-1}(y)={\begin{cases}\displaystyle {1 \over \lambda }\ln(2y)&y<{1 \over 2}\\\displaystyle -{1 \over \lambda }\ln(2(1-y)),&y\geq {1 \over 2}\end{cases}}}$.

A sequence can therefore be added to a sequence of standard random numbers ${\displaystyle u_{i}}$

${\displaystyle x_{i}:=F^{-1}(u_{i})}$

Calculate double exponentially distributed random numbers .

Relationship to other distributions

Relationship to normal distribution

If independent standard normal distributions are random variables, then standard laplace is distributed ( ). ${\displaystyle X_{1},X_{2},X_{3},X_{4}\sim {\mathcal {N}}(0,1)}$ ${\displaystyle Z=\det {\begin{pmatrix}X_{1}&X_{2}\\X_{3}&X_{4}\end{pmatrix}}=X_{1}\,X_{4}-X_{2}\,X_{3}}$ ${\displaystyle \mu =0}$

Relationship to the exponential distribution

A random variable , which is defined as the difference between two independent exponentially distributed random variables and with the same parameter, is Laplace distributed. ${\displaystyle X:=Y_{\lambda }-Z_{\lambda }}$ ${\displaystyle Y_{\lambda }}$ ${\displaystyle Z_{\lambda }}$

Relationship to the Rademacher distribution

If Rademacher is distributed and exponentially distributed to the parameter , then Laplace distributed to the position parameter is 0 and the scale parameter . ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \lambda }$ ${\displaystyle X\cdot Y}$ ${\displaystyle {\frac {1}{\lambda }}}$

Demarcation from constant uniform distribution

The continuous Laplace distribution defined in this way has nothing to do with the continuous uniform distribution . It is still often confused with it because the discrete uniform distribution is named after Laplace ( Laplace cube ).

Web links

• University of Konstanz - Interactive animation

swell

1. ^ Georgii: Stochastics. 2009, p. 225.
2. ↑ Milton Abramowitz and Irene Stegun : Handbook of Mathematical Functions , 1972, p. 930