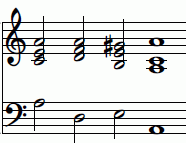minor
Moll (from Latin mollis , 'soft' ; French mode mineur , English minor , Italian modo minore , Spanish modo menor ) denotes a set of tones in music . This can refer to a key , a scale or a chord . Minor forms a pair of terms with major and shares its history of naming and meaning.
- major minor
The totality of all major and minor keys is also called the major-minor system . This replaced the church mode system in the 17th and 18th centuries .
Characteristic of the minor gender is the interval of a minor third between the fundamental and the third of the tone material. The minor third above the fundamental is therefore minor third called.
The effort to distinguish the names of major and minor in the typeface has resulted in numerous writing variants. The spelling preferred today is C major and C minor , but various alternative spellings are still in use. See the section on notations in the article Key .
For etymology see major: Etymologie .
Minor scale
Natural minor
The natural minor scale or pure minor scale of the "pure" or "Aeolian minor" or "natural minor" is a heptatonic scale with semitone steps between the second and third and the fifth and sixth steps and whole steps between the others. Since the 16th century, the minor scale has been the second most frequently used scale in Western music after the major scale .
The natural A minor scale consists exclusively of root tones : A, B, C, D, E, F, G, A.
Harmonic minor
The harmonic minor scale , the harmonic minor scale , is a variant of the natural minor scale in which the seventh degree is raised by a semitone. This is done in order to achieve the key note effect known from major also in minor. The dominant triad then becomes a major triad. For example, the seventh degree g is raised from a natural minor to the leading note g sharp .
The harmonic minor scale is a compilation of the tones that occur in a cadencing chord progression with a minor triad as the subdominant and a major triad as the dominant . Since the focus here is on the harmonic aspect, the name of this variant is explained.
Between the sixth and seventh steps there is a so-called hiatus step (three semitones). The hiatus, which gives the scale an oriental tone, was largely avoided in western music due to its unsangibility as a melodic step and is only found occasionally in instrumental music.
The notes of the harmonic A minor scale are: A, B, C, D, E, F, G sharp, A.
Melodic minor
The harmonic minor scale contains the difficult-to-sing hiatus step between the sixth and seventh degree. To avoid it, the sixth degree is also raised in the melodic minor scale . With the exception of the third tone (minor third to the root), the scale corresponds to the major scale.
Since the artificially generated leading tone is not necessary when going down, the natural minor is used - apart from the melodic minor in jazz .
The pitches of the melodic A minor scale upwards are: A, B, C, D, E, F sharp, G sharp, A.
For the inclusion of the ladder in the chord-scale theory , however, the different shape depending on the upward or downward movement of the ladder is useless. Therefore, only the upward form is used here and is called “ Melodic Moll upward ” (“MMA” for short). The MMA scale is the basis for many scales that are often used in jazz.
Gypsy minor
This further variant of the minor scale is used in gypsy music (especially the music of the Sinti and Roma ), but also e.g. B. used by Franz Liszt (Hungarian Rhapsodies ). It corresponds to the harmonic minor with a raised fourth degree. This creates a second excessive second step (hiatus) between the third and fourth degree, which - similar to the harmonic minor - creates a special oriental tone.
The notes of the A gypsy minor scale are: A, B, C, D-flat, E, F, G sharp, A.
Pictorial representations
Relationships to major
Major variant
The parallel key a minor key having the same root (e.g., A minor and A major ), but it has due to the difference in major gradation other sign or another preliminary drawing. The major variant is always three steps further in the circle of fifths than the underlying minor key, i.e. it always differs from it by three accidentals. So z. B. E minor with a cross , but E major with four crosses.
Major parallel
For every minor key there is a parallel key in major , also called major parallel, which contains the same tones and is therefore notated with the same preliminary drawing, but starts a minor third higher (for example A minor - C major ).
Counter-sound
The counter-sound of a minor chord is also a major chord, see also mediante .
The different effects of major and minor
Most people experience major and minor emotionally differently. According to recent scientific studies, however, small children lack the ability to make such a distinction and do not develop until they are around six years old.
Major is often associated with "happy" and minor with "sad". These associations are questionable, however, since they can lead to the assumption that all songs or pieces of music in major are happy, and all in minor are sad. This is wrong, however, because the emotional character of music is also determined by other components such as melody , rhythm and tempo , regardless of the type of tone . There are quite a number of minor songs with a happy character ( Kalinka ) and major songs with a rather sad character ( Am Brunnen vor dem Tore ).
The influence of the type of tone on the emotional character of the music can be described as follows: If, for example, an already sad major song is converted to a minor key, it will appear even sadder afterwards, while an already happy minor song sounds even happier in the major version. The gender of the tone is not decisive, but it does cause a shift in the quality of expression in one direction or the other.
Often one encounters a synaesthetic characterization of major and minor , which is more independent of emotional aspects, through adjectives that are borrowed from the realm of visual perception. Major is often described as “bright”, “clear” or “radiant”, and minor as “dark”, “gloomy” or “cloudy”. These characterizations have the advantage of greater generality over the emotional associations with “happy” and “sad”.
One acoustic reason for the different effects of major and minor is that the minor triad - compared to the major triad - has a lower sound value ( degree of consonance ). This lesser "melodious sound" of the minor triad is z. B. responsible for the fact that this, unlike the major triad, was not regarded as a conclusive consonance for a long time. It was only in the course of the Baroque era that the previously common practice of ending pieces of music in minor not with a minor but with a major triad (see Picardic third ) gradually disappeared .
Several independent reasons are used for the aforementioned difference in sound value between major and minor triad:
- In the overtone series z. B. the (capital) C contains a C major triad as the fourth, fifth and sixth overtone: c '- e' - g ', whereby the root is counted as the first "overtone". The C minor triad, however, does not appear in the overtone series of C.
The resulting different sound quality of major and minor triads can be illustrated by an experiment on the piano: If you strike a C with your left hand and at the same time a major chord consisting of c ', e' and g 'with your right hand, the result is a perfectly consonant sound. If, however, the major is replaced by a minor triad (c ', es', g'), the minor third rubbing it 'with the e', which resonates as the 5th overtone of the root C, so that one gets the impression of a rather dissonant sound wins. The experiment works even better with pure tuning than with the same level . - The phenomenon of combination tones can also be used to compare major and minor triads. A consideration of the first order difference tones is sufficient here, the frequencies of which result from the frequency difference of the individual tones involved. With the C major triad (c '- e' - g ') the difference tones of all the intervals (fifth, major and minor third) are: c, C and C, with the c minor triad (c' - es' - g ') accordingly: c, As 1 and Es. The combination of the tones in the minor chord is much more complicated and “more stressful” than in the major chord.
The acoustic differences described above do not play a role in a theory of the psychologist Norman Cook, who tries to justify the different effects of the major and minor triad in a different way by constructing a connection to the primeval animal and human sound behavior.
The "minor problem"
While the major triad ( root , major third and perfect fifth ) can easily be derived from the overtone series , corresponding attempts for the minor triad are not equally conclusive, which is why the explanation of the minor triad turns into a real problem, namely the so-called "minor problem “Expanded.
The minor triad (or chord ) consists of the root, the third and the fifth tone of the minor scale (s). If these intervals - regardless of the respective tuning - are interpreted as harmonic-pure (i.e. prime 1: 1, minor third 6: 5 and fifth 3: 2), the result is - analogous to the major triad 4: 5: 6 - the vibration ratio 10 : 12: 15.
- brought to a common denominator =
The minor chord thus also has an equivalent in the overtone series , but in contrast to the major chord this is problematic in several ways:
On the one hand, this minor triad is interrupted by intermediate partials (11, 13, 14), which gives it a more complex vibrational relationship than the major triad, and on the other hand, this so-called "monistic" (i.e. derived from the overtone series) interpretation of the minor chord has no clear fundamental , because the "producer tone" of the overtone series (here: C) does not match the prime of the triad (here: e 2 in E minor). According to Hugo Riemann's functional theory, this E minor chord is a so-called "alternating lead tone", a "pseudo consonance" that is made up of the two neighboring major chords (C major 8:10:12 and G major 12: 15:18) and thus equates to a bitonal construct. Many well-known music theorists of the 19th and early 20th centuries (such as Moritz Hauptmann , Arthur von Oettingen , Hugo Riemann and Sigfrid Karg-Elert ) did not consider this to be appropriate for the minor gender, as it resulted from both the more complex vibration ratio and the double keynote lets close a dissonant sound.
According to Paul Hindemith and many others, the minor chord, on the other hand, arises from the lower alteration ("clouding") of the major major third, which he saw legitimized by the inability of the listener or instrumentalist to differentiate between major and minor tones at sliding pitches ( glissando ):
“But what is the minor triad really? I consider it, following a theory that is no longer entirely new, to cloud the major triad. Since it is not even possible to properly separate the minor and major third from each other, I do not believe in a polar contrast between the two chords. They are the high and low, strong and weak, light and dark, haunting and dull versions of one and the same sound. "
In this "turbidity theory" of minor chord is, however, to an artificially generated Variant sound degrades, the vibration with its ratio of 4: 4 4 / 5 6 has no counterpart in the harmonic series. The minor third 6: 5 is created by a chromatic semitone step downwards ( e – es in C major / C minor), the so-called minor chroma 25:24:
- this also gives rise to the relationship
Johann Wolfgang von Goethe already spoke out against such a view .
From today's perspective, the almost esoteric interpretation of the minor chord as a “lower sound” with the vibration ratio (for fifth: third: prime, so in reverse order!) - that “polar opposite” rejected by Hindemith - also brings with it considerable problems. According to this doctrine (the so-called " harmonic dualism "), which was almost a generally valid consensus in musicology at the beginning of the 20th century , the reference tone of a minor triad is not its prime, but its fifth, without, however, the corresponding consequences for the musical sentence to be considered or demanded (e.g. doubling the fifth instead of the common prime). Furthermore, the objectively verifiable physical phenomenon of the overtone series is compared to a hypothetical, mathematically constructed, reciprocal undertone series as equivalent:

From this, the minor chord results as an interval- true , mirror-symmetrical inversion of the major triad, with the major third - viewed mathematically - as the arithmetic mean of prime 1: 1 and fifth 3: 2 and, conversely, the minor third as their harmonic mean ; an approach that Gioseffo Zarlino described in a similar way in “Le Istituzioni harmoniche” (1558):
Although the “harmonic dualism” thus creates the desired equality of major and minor, this derivation appeared to many critics (in particular the designation by von Oettingens, Riemanns and Karg-Elerts of a C minor triad as “sub-G” - with the cipher ° g, in contrast to c + for C major) not only unnecessarily complicated:
"But I haven't been so taught for a long time that I should choose the dualism and the designation of the minor chord."
Rather, this was also impractical and incompatible with the results of music psychology .
Despite the different doctrines on how to solve the "minor problem", the intonation of the minor chord itself remains unaffected and the results of one theory can be converted into those of the other, whereby from a (purely) mathematical point of view, preference is given to the simplest numerical ratio :
“Well,
that Mollakk is still used by many theorists today. is considered a Durakk. (!) with an altered (!!) third, is more to cry than laugh! A craftsman knows better about his material than these people, who ultimately still consider themselves “music scholars” ... The major chord in the S conception [vibration ratio] is the complex of 1 3 5 , resp. in close basic position 4: 5: 6. The minor chord is in S-view either 4: 4 4 / 5 (!): 6 or 10: 12: 15 . In the latter case, he would not have a prime to which the 12 (i.e. 6 or 3) could refer. Now, 4: 4 4 / 5 : 6 equal to 20 /5: 24 /5: 30 /5, di reduced 10: 12: 15, further di brought to General counter 60: reduced ! "
Some music theorists (such as Otakar Hostinský and Josef Achtélik ) tried to compensate for the weaknesses of the "monistic" minor theory by simpler numerical proportions of the minor chord, but this can only be done at the expense of the harmonic-pure intonation. The complex of 6th, 7th and 9th overtone, which apparently corresponds to a G minor triad ( g – b – d ), was up for discussion . Here, however, the pure little bit 6: 5 becomes the so-called “septimal small bit” 7: 6, which with its 266.87 cents appears to be a quarter tone (approx. 48.77 cents) too small. Such a triad 6: 7: 9 can at best be understood as part of the seventh non chord 4: 5: 6: 7: 9, i.e. a dissonant (!), Dominant (!) Major (!) Chord, and would also result as its major parallel ( b – d – f ) the (unusable) vibration ratio 7: 9: 10½ = 14:18:21 .
The 11th overtone, the so-called " Alphorn -fa", is even more problematic . At 551.318 cents (for the interval 11: 8), this is almost exactly between the pitches f ( tempered 500 cents) and f sharp (600 cents), and thus delivers “neutral thirds” 11: 9 (neither major nor minor). Such a neutral sound results from the vibration ratio 9: 11: 13½ = 18:22:27 ( d – f / f sharp – a ); at the 9th, 11th, and 15th overtone ( d-f / fis-h ), a reversal of the B minor chord, he on the other hand leads to a disgruntled wolf fifth 22:15 (about 663 cents) .
The “minor problem” thus remains one of the unsolved schisms in music theory, but it has hardly any meaning in musical practice. However, the juxtaposition of the three different minor scales and the artificially raised Picardian third at the end of a piece of music may have its origin in the less pronounced fundamental sense of the minor harmonic. In particular, the composers of the Romantic and Late Romantic periods , that is to say the composers of the time when the minor was stylized as a “problem”, saw the latent ambivalence of the minor gender not as a disadvantage but, on the contrary, an advantage. The harmony theory that is common today (such as that of Hermann Grabner or Wilhelm Maler ) suits them insofar as it gradually got rid of the speculative superstructure of the Riemannian functional theory and is more and more oriented towards the relationships of tempered mood.
See also
literature
- Wieland Ziegenrücker: General music theory with questions and tasks for self-control. German Publishing House for Music, Leipzig 1977; Paperback edition: Wilhelm Goldmann Verlag, and Musikverlag B. Schott's Sons, Mainz 1979, ISBN 3-442-33003-3 , pp. 88-93.
Web links
Individual evidence
- ↑ Dirk Bell : Jazz starts. Part III. In: Guitar & Lute. 6, 1984, No. 5, pp. 54-56; here: p. 54.
- ↑ To small children, music in a minor key doesn't necessarily sound sad . On: Wissenschaft.de of April 7, 2001.
- ↑ Manfred Dworschak: Valleys of euphony . In: Der Spiegel . No. 32 , 2008, p. 118-120 ( online ).
- ↑ Rudolf Klein: On the definition of bitonality. In: Austrian music magazine. Volume 6, 1951, p. 313; Klein, a convinced "monist" actually speaks of the "bitonality of the simple minor chord."
- ↑ Moritz Hauptmann: The nature of harmonics and metrics. Leipzig 1853.
- ↑ Arthur von Oettingen: Harmoniesystem in dual development. Studies on the theory of music. Dorpat / Leipzig 1866; Revised second edition as The dual harmony system. Leipzig 1913.
- ↑ Hugo Riemann: The problem of harmonic dualism. Leipzig 1905.
- ↑ Sigfrid Karg-Elert: Polaristic theory of sound and tonality. Leipzig 1930.
- ^ Paul Hindemith: Instruction in clay composition. I. Theoretical part. Mainz 1937.
- ↑ Hugo Riemann: The objective existence of undertones in the sound wave. Kassel 1875.
- ↑ see: Carl Dahlhaus: Was Zarlino a dualist? In: The music research. Volume 10, 1957, pp. 286ff.
- ↑ Else Hase-Koehler (ed.): Max Reger - letters from a German master - a picture of life. 2nd Edition. Leipzig 1938, p. 81.
- ↑ Otakar Hostinský: The study of musical sounds. Prague 1879.
- ↑ Josef Achtélik: The natural sound as the root of all harmonies. An aesthetic music theory in two parts. Leipzig 1922 and 1928.
- ^ Hermann Grabner: Handbook of functional harmony theory. Regensburg 1944.
- ^ Wilhelm Maler: Contribution to the major minor tonal harmony theory. Munich 1957.