Piezoelectricity

The piezoelectricity even piezoelectric effect or short piezo effect (of Alt Gr. Πιέζειν piezein , press', press' and ἤλεκτρον electron , Bernstein ') describes the change in electrical polarization , and thus the occurrence of an electrical voltage to solids, when elastically deformed be (direct piezoelectric effect) . Conversely, materials deform when an electrical voltage is applied (inverse piezo effect) .
history
The direct piezo effect was discovered in 1880 by the brothers Jacques and Pierre Curie . In experiments with tourmaline crystals , they found that mechanical deformation of the crystals creates electrical charges on the crystal surface , the amount of which is proportional to the stress. Today, PZT ceramics (such as lead-zirconate-titanate ) are mostly used for piezo elements .
Macroscopically , the effect could already be described in the context of continuum mechanics at the beginning of the 20th century. The microscopic description was only possible through a thorough understanding of the discrete structure of condensed matter . A more detailed microscopic treatise was given by Richard M. Martin in 1972.
The first applications were piezoelectric ultrasonic transducers and, soon after, quartz oscillators for frequency stabilization. With the patent on the charge amplifier granted to Walter P. Kistler in 1950 , piezoelectric measurement technology achieved its breakthrough for broad industrial application.
principle
By the directed deformation of a piezoelectric material to form microscopic dipoles within the elementary cells (displacement of the charge areas ). The summation of the associated electrical field in all unit cells of the crystal leads to a macroscopically measurable electrical voltage. Directional deformation means that the applied pressure does not act on the sample from all sides, but (for example) only from opposite sides. Conversely, a deformation of the crystal or the piezoceramic component can be achieved by applying an electrical voltage.
There are essentially three different effects:
- Longitudinal effect: the force creates a polarization in the direction of the force and the electrical voltage can be measured in the same direction.
- Transverse effect: The polarization is transverse to the force, so that the tension is created across the direction of the force.
- Shear effect: the tension is created diagonally to the shear planes .
All three effects can also be reversed; That is, a force can be generated by the action of a tension by changing the volume.
Like any other solid body, piezoelectric bodies can also perform mechanical vibrations. In piezoelectrics, these vibrations can be excited electrically and in turn cause an electrical voltage. The frequency of the oscillation depends only on the speed of sound (a material constant) and the dimensions of the piezoelectric body. With a suitable attachment, these natural frequencies are hardly influenced by environmental influences, which means that piezoelectric components such as oscillating crystals are very well suited for use in precise oscillators , for example for quartz watches .
Piezoelectric materials
Basics
The piezoelectric effect can first be explained by the change in geometry. This is the resistive piezoelectric effect. When stretched, i.e. longer and thinner, a wire has a higher resistance. In the case of metals, the piezoelectric effect is based solely on the change in geometry. Furthermore, all non-conductive ferroelectric materials and materials with a permanent electric dipole are also piezoelectric, for example barium titanate and lead zirconate titanate (PZT). However, only some of the piezoelectrics behave ferroelectrically.
In the case of crystals, the crystal symmetry is another criterion for the occurrence of piezoelectricity. The piezoelectric polarization does not occur when the crystal has a center of inversion. Piezoelectricity can occur in all 21 non-centrosymmetric point groups , with the exception of the cubic point group 432 . In other words, a unit cell must not have a point at which a point reflection converts the crystal into itself.
The best known material with piezo properties is quartz (SiO 2 ). Quartz crystals have the non-centrosymmetric point group 32 . Each Si atom sits in the middle of a tetrahedron made up of four oxygen atoms. A force acting in the direction of the base surface (crystallographic direction: [111]) now deforms these tetrahedra in such a way that the compressed tetrahedra are electrically polarized and a net voltage occurs on the surfaces of the crystal (in the [111] direction).
Technically used materials that show a stronger piezo effect than quartz are often derived from the perovskite structure, e.g. E.g .: barium titanate (BaTiO 3 ). The cubic perovskite modification itself has the centrosymmetric point group and is therefore non-piezoelectric, but below a critical temperature - the piezoelectric Curie temperature T C - the material can change into a non-centrosymmetric perovskite structure (rhombohedral / tetragonal, see lead Zirconate titanate ). It then shows a spontaneous polarization and has ferroelectric properties.
Piezoelectric Crystals
- The most important piezoelectric crystal is the trigonal crystal structure α-quartz formed by quartz, which is stable up to 573 ° C. The most important application are quartz crystals.
- Lithium has to quartz higher piezoelectric constants and for piezoelectric filters and SAW devices (ger .: surface acoustic wave , surface acoustic wave ) is used.
- Gallium orthophosphate has only been available as a piezoelectric material since the 1990s. This material is similar to quartz, but has higher piezoelectric constants and better temperature stability. It is stable up to over 900 ° C.
Other piezoelectric crystals are berlinite , minerals of the tourmaline group , seignette salt and all ferroelectrics such as barium titanate (BTO) or lead zirconate titanate (PZT). However, BTO and PZT are normally not used as single crystals, but in polycrystalline form (ceramics).
Compared to piezoelectric crystals, piezoelectric ceramics such as PZT have the advantage of significantly higher piezoelectric coefficients. The advantages of the crystals quartz, gallium orthophosphate and lithium niobate are higher temperature stability, lower losses, significantly lower hysteresis and hardly any creep (i.e. delayed deformation) after changing the applied voltage.
Piezoelectric ceramics
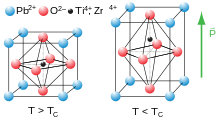
Industrially produced piezo elements are mostly ceramics . These ceramics are made from synthetic , inorganic , ferroelectric and polycrystalline ceramic materials. Typical base materials for high-voltage actuators are modified lead-zirconate-titanate (PZT) and lead-magnesium-niobate (PMN) for low-voltage actuators .
The composite of the PZT ceramics (Pb, O, Ti / Zr) crystallizes in the perovskite crystal structure. Below the piezoelectric Curie temperature, distortions of the ideal perovskite structure create a dipole moment .
In ceramic piezo elements, the internal dipoles are still disordered after the sintering process , which is why there are no piezoelectric properties. The Weiss districts or domains have an arbitrary spatial orientation and balance each other out. A clearly measurable piezoelectric property can only be impressed by an external constant electric field with a few MV / m, whereby the material is heated to just below the Curie temperature and then cooled again. The imprinted orientation is then largely retained ( remanent polarization ) and is referred to as the polarization direction .
Sintered piezo elements are characterized by efficiencies of 25% - 50% and permittivity numbers ε r around 1000.
The rotation of the Weiss domains by polarization leads to a slight distortion of the material and a macroscopic increase in length in the direction of polarization.
Other piezoelectric materials
- Piezoelectric thin films are also increasingly being used as active sensor materials . With the help of semiconductor technologies it is possible to deposit these active piezoelectric thin films on silicon. This is mostly zinc oxide (ZnO) or aluminum nitride (AlN).
- The plastic polyvinylidene fluoride (PVDF) can be polarized - similar to piezoelectric ceramics - and is then piezoelectric. Applications for this are hydrophones .
Biological tissue
A piezoelectric effect was discovered for bones in 1957. These react piezoelectrically to loads . In 1967 a piezoelectric effect was also demonstrated for the soft tissue types skin, connective tissue and cartilage. In particular, collagen fibrils and fibers react piezoelectrically to pressure, tension and torsion. According to current knowledge, however, the aorta is not piezoelectric.
calculation
The macroscopic description in the context of continuum mechanics is shown below. Only a linear approximation is taken into account between the sizes considered. Nonlinear effects such as electrostriction are neglected here.
geometry
A coordinate system is selected to describe the spatially different properties . An x, y, z coordinate system is usually used for indexing, the axes of which are denoted by the numbers 1, 2, 3 (axis 3 corresponds to the polarization axis). The shearings on these axes are numbered 4, 5, 6. Based on these axes, the piezoelectric properties are expressed in equations with tensors .
Equations
The simplest equations for the piezo effect contain the polarization P pz (unit [C / m²]) and the deformation S pz ( dimensionless quantity ):
where d, e are the piezoelectric coefficients, E is the electric field strength (V / m) and T is the mechanical stress (N / m²). The first equation describes the direct, the second the inverse piezo effect.
The piezoelectric coefficients are described by three-stage so-called piezoelectric tensors . On the one hand you have:
- piezoelectric distortion coefficients (reaction of the distortion to the electric field)
- ; on the other hand
- piezoelectric stress coefficients (reaction of the mechanical stress to the electric field)
The two coefficients can be related to the elastic constants :
Second order effects (inverse piezo effect) are described by the electrostrictive coefficients.

The tensors given above are usually rewritten in matrix form ( Voigt notation ). This results in matrices with hexavalent components that correspond to the axis definition shown above. The piezoelectric effects are then described by means of two coupled equations in which the dielectric displacement D is used instead of the polarization.
- Permittivity at constant mechanical stress
- Constant of elasticity with constant electric field strength
It is common practice to summarize the elements of these equations in the coupling matrix. The most important material parameter for the inverse piezo effect and thus for actuators is the piezoelectric charge constant d. It describes the functional relationship between the applied electric field strength and the strain generated by it. The characteristic sizes of a piezoelectric transducer are different for the different directions of action.
In the area of actuators , two main effects are relevant. For these two effects, the equation for the expansion is simplified as follows
-
Piezoelectric cross or transversal effect (d 31 effect). The mechanical force acts across the applied field.
-
Piezoelectric longitudinal or longitudinal effect (d 33 effect). The mechanical force acts parallel to the applied field.
Applications
Today, piezoelectric components are used in many sectors: industry and manufacturing, the automotive industry, medical technology, and telecommunications. In 2010, the worldwide market for piezoelectric components achieved sales of approximately 14.8 billion US dollars.
In general, the applications can be divided into three areas:
Sensors
The occurrence of the piezoelectric charge in the event of mechanical deformation is used in force, pressure and acceleration sensors. The resulting charge can be converted into an electrical voltage with a low source impedance using a charge amplifier . With the other option of charging a capacitor with this charge and measuring its voltage with a voltage measuring device with the highest possible resistance, poor insulation resistances, for example due to moisture, can strongly falsify the result and prevent slow deformations from being recorded.
- Piezo elements are used in music as pickups for acoustic instruments, mainly for stringed instruments such as guitar , violin or mandolin . The dynamic deformation of the instrument (vibration of the sound body) is converted into a low alternating voltage , which is then amplified electrically .
- In the case of piezoelectric acceleration sensors or pickups, mechanical deformation (compression or shear) results in charge separation due to the acceleration and thus a charge that can be tapped on the vapor-deposited electrodes.
- In the case of quartz oscillators, the influence of various sizes on the resonance frequency can be used , and in the case of surface acoustic wave components, the influence on the delay time can be used. An important application is the measurement of the mass applied to the quartz, e.g. B. in industrial coating processes to determine the layer thickness. The temperature dependence of the oscillation frequency can also be measured; however, such oscillating quartz thermometers are no longer on the market.
Actuators
Piezo actuators can be differentiated according to the mode of operation (quasi-static or resonant) or according to the direction of the effect used. The distinction between transverse effect (transverse effect, d31 effect), longitudinal effect (longitudinal effect, d33 effect) and shear effect (d15 effect) results in three different basic elements for piezoelectric actuators. However, the shear effect is used significantly less often than the other two effects in actuators, since d15 actuators are more complex to manufacture. For multi-dimensional movements, several piezo elements have to be combined in such a way that they act in different directions.
Even actuators that operate in the kHz range can be regarded as quasi-static, as long as the operating frequency well below the first resonant frequency is the system. The high accuracy and the great dynamics predestine the piezo actuator for positioning tasks and for active vibration damping. Typical changes in length and thus travel ranges are 0.1% of the actuator length and therefore in the order of 100 µm for the largest actuators available. The electric strength of the material, the high operating voltages and the saturation curve of the material have a limiting effect on the travel ranges. The short travel ranges of piezo actuators can be increased by various means, e.g. B. by lever or by special designs such as the bimorph bending element. This is a combination of two transverse expansion elements. Opposite polarization or control of the elements causes the actuator to bend.
Examples of the quasi-static application of piezo actuators are
- Braille displays for the blind, in which, by applying a voltage, tactile pens are pushed up for the blind, whereby the monitor text is converted into tactile Braille characters on the PC.
- Inkjet printer ( drop-on-demand )
- Piezo loudspeakers in which the sound waves are generated by an audio-frequency alternating voltage
- Diesel injection systems with piezoelectric actuators (ceramic multilayer components with noble metal inner electrodes) which have improved common rail technology . This partially replaces the injection of diesel via valves. Piezo actuators have also been used in the pump-nozzle system since 2005 . Industrial companies that manufacture such piezo actuators in large numbers are Epcos and Bosch .
Piezo actuators operated resonantly are mainly used to generate ultrasound and in piezo motors such as B. traveling wave motors are used. In piezo motors, the small travel ranges of piezo actuators are added up using various principles, so that very large travel ranges can be achieved. Depending on the motor principle, piezomotors work quasi-statically or resonantly.
Electrical components
In these applications, a mechanical vibration of a piezoelectric solid is electrically excited and again electrically detected. A fundamental distinction is made between two types
- Volume resonators in which essentially the entire piezoelectric element oscillates. The most important representatives are quartz crystals and ceramic filters.
- SAW devices based on surface acoustic waves (Engl. Surface acoustic wave , SAW). Examples are SAW filters and delay lines.
The piezoelectric transformer is used as a component as a form of resonance transformer for generating the high voltage in the area of the inverter . It is used to supply fluorescent tubes (CCFL), such as those used as background lighting in liquid crystal displays .
Other uses
The piezoelectric effect is used in piezo lighters , where a sudden high pressure (hammer) is used in a piezo igniter to generate a brief high electrical voltage. The spark discharge then ignites the gas flame. Impact fuses such as in the warheads of anti-tank weapons (Panzerfaust / RPG-7 ), piezo microphones (crystal microphones ), piezo loudspeakers in headphones, batteryless radio switches, piezo sirens and buzzers are further uses.
A number of micromechanical sensors make use of piezoelectricity, e.g. B. acceleration sensors , yaw rate , pressure and force sensors as well as ultrasonic sensors, microbalances and knock sensors in motor vehicle engines.
Some micromechanical actuators are also based on piezoelectricity: Piezomotors (squigglers), ultrasonic motors , e.g. B. for lens autofocusing or clock drives , in the field of micro and nanopositioning systems are scanning tunneling microscope , scanning electron microscope and the atomic force microscope piezoelectrically driven systems. In valve technology , injection nozzles from cars (series production started in 2000 for diesel engines), proportional pressure regulators and print heads from inkjet printers should be mentioned. Pickups , electroacoustic delay lines as in older PAL or SECAM color televisions, batteryless radio technology (switches) and optical modulators are also piezoelectric components. The feeding technology uses many of the components mentioned. The piezoelectric crystal is also used to generate cold atmospheric pressure plasma, which is mainly used for surface activation , germ reduction and odor reduction in medicine.
Similar effects
Web links
- PiezoMat.org - Online database on piezoelectric materials, their properties and applications
- Piezotransfer.de - platform for bundled knowledge of the piezoceramic industry
- The piezo effect in crystals
- Piezo tutorial - Piezo actuators in precision control technology
- Breviary Technical Ceramics - lead zirconate titanate, piezoelectric effect
- Piezo booklet - interesting facts about piezo mechanics
- Piezoelectric direct discharge plasma - plasma generation
Individual evidence
- ^ Richard M. Martin: Piezoelectricity . In: Physical Review B . Vol. 5, No. 4 , 1972, ISSN 1098-0121 , pp. 1607-1613 , doi : 10.1103 / PhysRevB.5.1607 .
- ↑ a b Ekbert Hering; Rolf Martin; Martin Stohrer: Physics for Engineers . 12th edition. Springer-Verlag, 2016, ISBN 978-3-662-49354-0 , 9.3.3 Piezoelectricity.
- ↑ Researchers get straight to the heart of piezoelectric tissues. In: Phys.org, American Institute of Physics. October 5, 2017, accessed December 5, 2018 .
- ↑ Eiichi Fukada, Iwao Yasuda: On the Piezoelectric Effect of Bone . In: Journal of the Physical Society of Japan . tape 12 , no. 10 , 1957, pp. 1158-1162 , doi : 10.1143 / JPSJ.12.1158 .
- ↑ Morris H. Shamos, Leroy S. Lavine, piezoelectricity as a fundamental property of Biological Tissues , Nature, Vol 213, pp 267-269, January 21, 1967
- ↑ Hartmut Heine: Textbook of biological medicine: Basics and Extrazellutäre Martix , Haug Verlag, 2015, ISBN 978-3-8304-7544-6 . P. 42 .
- ↑ Thomas Lenz et al, Ferroelectricity and piezoelectricity in soft biological tissue: Porcine aortic walls revisited , Applied Physics Letters (2017), doi: 10.1063 / 1.4998228 .
- ↑ Market Report: World Piezoelectric Device Market . Acmite Market Intelligence . Retrieved July 27, 2011.
- ↑ Dr. Stefan Nettesheim: Innovative plasma generator in piezo technology: Applications in medicine and medicaltechnology. (PDF) October 29, 2015, accessed on March 5, 2019 .


















