Rhombus

This article describes a geometric shape. For further meanings, see diamond (disambiguation) .

Properties of a diamond:
two sides are parallel to each other and the connecting lines of the opposite corners intersect at right angles.

A rhombus or rhombus (from Latin rhombus , circular body, top, shifted square, diamond, rhombus' ; this from ancient Greek ῥόμβος rhómbos with the same meaning) in geometry is a flat square with four sides of equal length. Opposite sides are parallel and opposite angles are the same size.

etymology

The Etymological Dictionary of the German Language sees a use of the geometric term "Raute" (Middle High German rūte from Old High German rūta , borrowed from Latin ruta ) since the 14th century and calls the origin "dark". According to the editions from 1934 to 1975, a rhombus would result if the tips of the four petals of the rhombus were connected by straight lines. The first use in geometry is attested for 1539. Later editions no longer contain this explanation and only use a technically equivalent late Middle High German form rūta . Botanical etymological lexicons indicate that the rue does not have a rhombic leaf blade. According to the Etymological Dictionary by Wolfgang Pfeifer , the term arose from the "first appearing in heraldry geometric figure in the stylized four-part flower shape of the plant" as a borrowing from Latin rūta , Greek rhȳtḗ (ῥυτή) (“bitter herb”).

Designations and representations

Double cross, rhombus and star on a calculating machine

→ Main articles : Diamond (heraldry)  and diamond (symbol)

In addition to “diamond”, the terms “rhombus” (plural: rhombuses) and “diamonds” are used. For example, a weave pattern in textiles is called "checked pattern".

A square that is on the top is sometimes also referred to as a diamond in general terms. Usually a square is shown lying on its side (parallel to the edge) , so an upside-down square looks more like a diamond.

Diamond shapes as characters can be found in Unicode in the block Geometric Shapes , for example ◆ (U + 25C6 black diamond "full-surface diamond "), ◇ (U + 25C7 white diamond "hollow diamond ") and ◊ (U + 25CA lozenge "rhombus").

"Rhombus" also denotes the symbol ⌗ (U + 2317 viewdata square ) on the telephone keypad , which, according to recommendation ITU-T E.161 of the International Telecommunication Union, is optionally available as a square or as a rhombus with an interior angle of 80 ° at the bottom left and at the corners 8–18% of lines extending beyond the edge length of this shape are to be displayed.

The similar double cross # (U + 0023 number sign ) is also misleadingly referred to as a “diamond” (for example in DIN 5008). On the surface, however, the double cross does not have much resemblance to an ordinary diamond, in common fonts it encloses a parallelogram on the inside and this is not a diamond in the narrower sense.

In heraldry , diamond-shaped elements are also called wecke and spindle , and the square on top is also called an edge cube.

properties

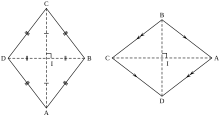
A diamond is a flat square with four sides of equal length . Alternatively, the diamond can be defined as a parallelogram , the diagonals of which intersect at right angles (see orthodiagonal square ).

The following applies to each diamond:

• Opposite sides are parallel .
• Opposite interior angles are the same size, neighboring interior angles are supplementary , i.e. that is, their sum is 180 °.
• The interior angles are halved by a diagonal.
• The two diagonals are perpendicular to each other and bisect each other.
• It has an inscribed circle and is therefore a tangent square . The center of the circle is the intersection of the diagonals .
• The diagonals are axes of symmetry . The two axes of symmetry are therefore perpendicular to one another.
• It is point-symmetric (twofold symmetric) with respect to the intersection of the diagonals.
• The symmetry group is the Klein group of four .

The diamond can be characterized as

• Parallelogram with two adjacent sides of equal length
• Parallelogram with orthogonal diagonals
• Parallelogram with a diagonal bisecting an interior angle
• Dragon square with parallel sides in pairs
• Square with orthogonal diagonals bisecting each other
• Square with two diagonals bisecting an interior angle
• Parallelogram with a diagonal bisecting an interior angle

To construct a rhombus, two determinants are required, e.g. B. the side length and an angle , necessary.

Formulas

Diamond decoration on the gable of the south transept of St Julien , Chauriat , Auvergne

Mathematical formulas for the rhombus
Area	${\displaystyle A=a\cdot h_{a}}$
	${\displaystyle A={\frac {e\cdot f}{2}}}$
	${\displaystyle A=a^{2}\cdot \sin(\alpha )=a^{2}\cdot \sin(\beta )}$
	${\displaystyle A={\frac {h_{a}^{2}}{\sin(\alpha )}}={\frac {h_{a}^{2}}{\sin(\beta )}}}$
scope	${\displaystyle u=4\cdot a}$
Side length	${\displaystyle a={\frac {1}{2}}\cdot {\sqrt {e^{2}+f^{2}}}}$
Length of the diagonal	${\displaystyle e=2\cdot a\cdot \cos \left({\frac {\alpha }{2}}\right)=2\cdot a\cdot \sin \left({\frac {\beta }{2}}\right)}$
	${\displaystyle f=2\cdot a\cdot \sin \left({\frac {\alpha }{2}}\right)=2\cdot a\cdot \cos \left({\frac {\beta }{2}}\right)}$
height	${\displaystyle h_{a}=a\cdot \sin(\alpha )=a\cdot \sin(\beta )}$
Inscribed radius	${\displaystyle \rho ={\frac {h_{a}}{2}}={\frac {a\cdot \sin(\alpha )}{2}}={\frac {a\cdot \sin(\beta )}{2}}}$
Interior angle	${\displaystyle \alpha +\beta =180^{\circ }}$

Combinations of several diamonds

Diamond decoration on the gable of the south transept of the Church of St Étienne in Beauvais , Picardy

The star (“diamond star”) is only joined by diamonds whose central angle (i.e. the angle at the top where they are placed next to one another) is equal to a natural number . They then form a -pointed star . This does not apply to the three-dimensional case, in this case diamonds with different angles can also be joined at their tips and then result in pyramid-shaped tips. ${\displaystyle 360^{\circ }/n}$ ${\displaystyle n}$ ${\displaystyle n}$

Parquet with diamonds

• Due to its definition, each diamond is suitable for area-wide tiling , but only in two main directions (see platonic tiling ). Here the diamond tiling (with its special shape, the square grid , i.e. an orthogonal grid) forms one of the 17 possible symmetry groups of the tiling .
• Such tiling (area-filling, oblique-angled platonic tiling) can be found on the state flag of Bavaria (diamond flag) , heraldic technical jargon: obliquely roughened .
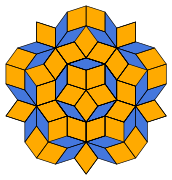
• A special feature is the aperiodic (quasi-crystalline) Penrose tiling of two rhombuses with interior angles of 36 ° and 144 ° or 72 ° and 108 °.

• 

  Floor mosaic from Pella , Old Macedonia

• 

  State flag of Bavaria (diamond flag)

• 

  Rhomb parquet with 3D effect (colored triangular grid )

• 

  Penrose tiling

Rhomb roof of the Marienkirche in Dortmund

Polyhedron with rhombuses

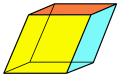
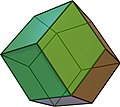
Some polyhedra have diamonds on their faces , for example the rhombohedron . The surface of the rhombic dodecahedron and rhombic triacontahedron , two Catalan solids , consists of congruent diamonds. Rhombohedra, rhombic dodecahedron and rhombic triacontahedron are polyhedra that are bounded exclusively by diamonds. The polyhedra mentioned are rotationally symmetrical , ie they can be mapped onto themselves by rotating about certain axes of rotation .

• 

  Rhombohedron

• 

  Rhombic dodecahedron

• 

  Rhombic triacontahedron

Rhombuses in architecture, art and design

This article or the following section is not adequately provided with supporting documents ( e.g. individual evidence ). Information without sufficient evidence could be removed soon. Please help Wikipedia by researching the information and including good evidence.

A diamond mosaic made of pebbles in the old Macedonian capital Pella dates from the Alexandrian period (see illustration above ). Abstract diamond patterns were popular as apotropaic symbols in the art of the Berbers in the Maghreb . In European art, however, they are rarely found, examples can be found in the decor of the south side of the priory church of St-Julien in Chauriat or in the gable of the north transept of the church of St Étienne in Beauvais .

• 

  Six-pointed diamond star

• 

  The Agyle pattern is sometimes called diamond pattern called

• 

  Renault logo (1972)

• 

  Sculpture by Victor Vasarely at the Budapest South Railway Station

• 

  Rue blossom (Ruta graveolens)

The rhombic roof is a tower roof made up of four diamond-shaped roof surfaces. The roof slopes are offset by 45 degrees compared to the gable walls.

The rhombus or lozenge formwork is used to clad facades or for privacy screens. The cross-section of the horizontally mounted slats forms a parallelogram. In contrast to ordinary slats, diamond-shaped slats form a drip edge on the front .

Web links

Commons : rhombus  - collection of images

Wiktionary: rhombus  - explanations of meanings, word origins, synonyms, translations

• Further information, calculation examples and illustrations

Individual evidence

1. ^ Karl Ernst Georges : Comprehensive Latin-German concise dictionary . 8th, improved and increased edition. Hahnsche Buchhandlung, Hannover 1918 ( zeno.org [accessed on March 12, 2020] dictionary entry “rhombus”).
2. ^ Wilhelm Pape , Max Sengebusch (arrangement): Concise dictionary of the Greek language . 3rd edition, 6th impression. Vieweg & Sohn, Braunschweig 1914 ( zeno.org [accessed on March 12, 2020]).
3. ↑ diamond . In: Friedrich Kluge: Etymological dictionary of the German language . 11th edition 1934, 21st edition 1975, 25th edition 2011.
4. ↑ Ruta . In: Helmut Genaust: Etymological manual of German plant names . 3rd edition 1989. Subsequent Ruta graveolens L. In: Friedhelm Sauerhoff: Etymological dictionary of German plant names . 2nd Edition. 2004.
5. ↑ Wolfgang Pfeifer: Etymological Dictionary of German . online , accessed April 3, 2019
6. ↑ diamond. Overview of meanings. Duden, accessed December 8, 2015 . "1. Rhombus 2. (EDP, telephony) Short form for: hash sign “. 
   
   
7. ↑ pound sign. Overview of meanings. Duden, accessed December 8, 2015 . “Characters in a text, on a keyboard, which consists of a cross made up of two horizontal and two oblique vertical lines: #; Short form: diamond ". 
   
8. ↑ Proven by Yevgraf S. Fedorow 1891, after Ian Stewart : Pentagonal tiles. In: Spectrum of Science. January 2000, pp. 106-108 (ill. P. 108).