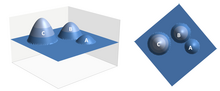
Notch height

Schematic representation of dominance and notch height of a mountain in a topographic map (below) and a corresponding projection of the relief (above). The decisive criteria for the dominance and notch height of mountain "B" are shown in each case. The notch height of mountain "B" corresponds to the difference between the summit height (here 531 m) and the amount of the contour line that surrounds it, but not a higher mountain (here 441 m, dashed line on the map).

Determination of the notch height of the 716 m high Great Shunner Fell . The green path to the next higher mountain, the 736 m high Whernside, has to descend to 324 m (point B), the red path to the more distant 745 m high Little Fell only up to 419 m (point A). All other paths continue to descend. Point A is the reference chart. Here it becomes clear that it is neither a direct route nor the nearest higher mountain.

The notch height or prominence , also called notch depth or relative saddle , is a measure of the independence of a peak , mountain or other geomorphological landform . In addition to dominance , it is an important criterion for classifying a mountain as such. In the case of a less pronounced elevation, for example on a ridge or plateau , the notch height is comparatively low, and one then speaks of a secondary peak or a ridge elevation.

Definitions

The notch height of a summit is the difference between its height and the highest notch (reference notch, English : key col ) , up to which one must at least descend in order to reach a higher peak.

The notch height of a summit is its height above the lowest closed contour line that surrounds it and at the same time does not include a higher peak.

The two definitions are synonymous if one disregards the fact that the first cannot be applied to the highest mountain on earth, as there is no higher peak.

The concept of relative immersion was presented by Klaus Hormann in 1965.

Thought experiment for illustration

If one imagines that the sea level rises until the last land connection between the mountain in question and any higher land point is flooded, i.e. the peak in question begins to form the highest point of an island, then its notch height corresponds exactly to its height above that (then existing) sea level, and the last flooded terrain bridge is its reference gap.

Terms and conventions

If a mountain forms the highest peak of a land mass, then its notch height is equal to its height above the sea. The sea is also seen as a possible gap.

The notch height of the highest mountain on earth, Mount Everest , corresponds according to the second definition given to its height above the sea of 8848 m .

Assuming that no two notches are exactly the same height, there is exactly one reference notch for each mountain. Conversely, each notch can only be used as a reference notch for a specific mountain, if one assumes that ridges do not branch out at notches.

A normalized (scaled) derived value is the orographic dominance , which sets the notch height in relation to the height .

Reference mountains

Apart from Mount Everest, you can get to at least one higher mountain for every peak beyond the relevant notch (including sea level). Some of these mountains with certain characteristics are variously listed as special reference mountains for the prominence of the respective summit. In the predominantly English-language literature, they are referred to as parent mountains . Some common concepts are presented below.

Line parent

The line parent of a summit is the next higher summit on the other side of the reference notch, following the course of the ridge, which can be reached without having to descend further. Since the line parent itself should have a certain independence, a minimum notch height must be set for it (cf. independence of mountains and peaks in high mountains ). Depending on which value you set here, you can get different line parents for the same peak. In addition, various approaches have been taken as to how the line parent is to be determined if, for example, B. divides the ridge beyond the reference chart and you have the choice between two higher reference mountains. Ron Tagliapietra , for example, suggested using the closest higher peak - measured along the ridge - as the reference mountain, even if this is the lower of the two candidates.

Jochberg's Prominence Master Series

Island parent series of the Jochberg . The heights of the peaks rise, those of the reference loops fall.

Prominence Master

The prominence parent of a summit, often also referred to as the prominence master , is the more prominent summit that follows the ridge and can be reached via the reference notch without having to descend deeper. The Prominence Master is always higher than the starting peak. Since it always has a greater notch height than the exit summit, one can speak of ancestry here in the real sense. At the same time, the definition of a minimum notch height , as required for the Parentage line , is avoided. For each peak, a series of ever higher and more prominent mountains can be determined, which begins with the peak and ends at the highest mountain of the respective land mass (island or continent).

Even so, the Prominence Master is not clearly determined in every case, for example in the case of ridge branches behind the reference slit. The Englishman Peter Ridges has therefore formulated a decision regulation according to which the peak is considered to be the parent whose lowest point in the ridge course after the ridge branching is higher than the lowest point on the connecting ridge of another candidate (" higher lowest point property ").

Three mountains form an island.

The island parent of peak A is mountain B. (From B - at a lower water level - it is mountain C.)

Iceland Parent

Comparable to the definition of the notch height above, one can imagine that the sea level rises until the last connection to a higher mountain as a headland just protrudes from the water. Thus, the summit is connected to another land mass to form a single island, the highest point of which is known as the Island Parent or Encirclement Parent . Apart from a few special cases, such as craters with central mountains, the Island Parent can be imagined as the highest peak that can be reached starting from the respective reference chard via a path that climbs at each point. It is therefore also the next higher mountain whose own reference chart is lower than that of the mountain under consideration. In contrast to the Line Parent and Prominence Master , the Island Parent is clearly defined from the start. As with the Prominence Parentage , a clear “lineage” with more prominent island parents can be determined for each peak . For comparatively low elevations, the determination of the island parent often leads to trivial results: For example, for European mountains whose reference chart is lower than the reference chart of Mont Blanc (113 m) - this applies to many elevations near the coast - the island parent is always the one Mount Everest.

While each mountain has exactly one reference notch and each notch is reference for exactly one mountain, several mountains can have the same parent mountain.

Examples

To go from the highest mountain in Austria, 3798 m above sea level. A. high Großglockner , to reach a higher mountain, you have to descend at least as far as the Brenner Pass ( 1370 m above sea level ). The difference in height results from the difference in height of 2428 m. This makes the Großglockner the second most prominent mountain in the Alps. The next higher mountain in a possible ridge, which can be reached via the Brenner Pass without having to descend deeper ( Line Parent ), is the 3905 meter high Ortler in South Tyrol , which at 1953 meters has a lower notch height than the Grossglockner itself. The next higher geographical neighbor of the Großglockner as the crow flies ( dominance ) is the 3851 meter high Königspitze , which is adjacent to the Ortler , but seen from the Brenner Pass along the ridge behind the Ortler. The Prominence Master and Island Parent of the Großglockner is Mont Blanc , which at 4810 meters is the highest alpine peak.

The second highest mountain in Austria, 3768 m above sea level. A. high Wildspitze in Tyrol , is hardly inferior to the Großglockner in height. Although it shares the Island Parent (Mont Blanc) with it, its Prominence Master is the Finsteraarhorn ( 4274 m above sea level ) in the Bernese Alps , which can be reached via the 1507 m slm high Reschen Pass , which acts as a reference chute . At 2279 m, the prominence of the Finsteraarhorn lies between that of the Glockner (2428 m) and that of the Wildspitze (2261 m). The prominent saddle of the Finsteraarhorn is at an altitude of 1995 m above sea level. M. at the Simplon Pass . Mont Blanc, Großglockner, Finsteraarhorn and Wildspitze are the four most prominent mountains in the Alps.

The Prominence Master and Island Parent of Mont Blanc is the highest mountain on earth, the 8848 m high Mount Everest in the Himalayas . The geographically closest higher mountains, however, are in the much closer Caucasus . The Kjukjurtlju (4912 m), which is close to the Elbrus (5642 m), is the dominance reference mountain for Mont Blanc.

Example of the distinction rule according to Peter Ridges : The Zugspitze has the Fernpass as a reference charter . The ridge beyond the reference gap runs north of the Inn to the west to a possible Prominence Parent . North of the source of the Inn, the ridge branches off to the candidates Finsteraarhorn and Piz Bernina - both are higher and more prominent than the Zugspitze. The Piz Bernina is much closer along the ridge, but the ridge from the junction to Piz Bernina has its lowest point in the 1815 meter high Malojapass . This height does not have to be fallen below on the ridge from the branch to the Finsteraarhorn, so that the Finsteraarhorn can be determined as the prominence parent of the Zugspitze.

To get from the Großer Hundstod (2593 m) in the Berchtesgaden Alps to a higher summit, you have to descend at least to the Dießbachscharte (2119 m). B. to the Schönfeldspitze (2653 m) or the Selbhorn (2655 m) in the Steinerne Meer . This results in a notch height of 474 meters. It can also be seen here that the height of the notch does not necessarily correspond to the height of a peak above the notch that leads to the next higher mountain. Because the next higher mountain in this case is the Watzmann (2713 m), but to get to it you have to descend even further to the Trischübelpass at 1774 meters. The Prominence Master and also the Island Parent for the great dog death is the Hochkönig , which as the highest mountain in the Berchtesgaden Alps has the largest notch height in the Northern Limestone Alps and is therefore one of the most prominent peaks in the entire Alpine region.

Independence of mountain groups, mountains and peaks

Magnitude of the rel. Saddle
mountains	150 m
Mountain groups	500 m
Main groups	1000 m
Large groups	2000 m

Mountain classifications

For the geomorphometric classification of mountain groups, Hormann developed the degree of relative saddle (see table). In contrast to mountains, the definitions mentioned at the beginning are not the same because a mountain group does not have to be surrounded by a closed contour line (or one that does not contain a higher peak): Here, however, the prominence of the group is always the notch height of their highest mountain above the highest notch of its boundary line.

In fact, such systems have not prevailed in mountaineering because the groups - apart from being metrically precise - have hardly any advantages. In particular, the breakdowns achieved in this way do not have the same area: In the Alps, for example, among the ten mountains with the highest notch height , the Hochkönig ( Berchtesgaden Alps and Dienten Mountains group ) is a very small group compared to the other dominant groups, and among the 13 mountains with Scharten heights of more than 2000 m with the Säntis ( Alpstein region ) another.

High mountains

In the Alps, according to a specification made by the UIAA , an elevation is considered a summit if its notch height is at least 30 meters. In order to speak of a mountain in its own right for a summit, a minimum height of approx. 100 to 300 meters is specified for the Alps. In the Himalayas even 500 meters can be found as a value.

The term Ultra Prominent Peak can be found in English literature for the 1500 mountains around the world with a notch height of more than 1500 meters (44 of them are in the Alps) .

In addition to the objective criteria such as dominance and notch height, however, subjective factors are also determining in practice for the designation as a mountain. For example, the alpine significance, the view from the summit, the optical dominance from the valley or the entry on a map can be decisive for an elevation to be called a mountain. So there are both well-known and alpine important summit points with very low heights as well as, conversely, mountains that are not even named despite being highly independent.

Low mountain range

Also in the low mountain range the notch height is used to determine the independence of mountains. This makes it necessary to adjust the numbers, as the height differences there are less than in the high mountains and gaps of 300 m are extremely rare. For the independence of peaks, minimum notch heights of 11 to 14 meters are used, depending on the altitude. However, so far there are no binding values that cover all of the altitudes relevant for low mountain ranges and are generally recognized. The determination of uniform values for the minimum height of the notch for independent low mountain range peaks is made more difficult by the fact that the mountains are traditionally defined here by their subjective appearance and there is generally no need to redefine the height of the notch. Not least because of this, the term Schartenhöhe is much less established in literature and general awareness with regard to low mountain ranges than with regard to high mountains.

literature

Theory:

Peter Grimm, Claus Roderich Mattmüller (ed.): The mountain groups of the Alps. Views, systematics and methods for the division of the Alps (= Wissenschaftliche Alpenvereinshefte. H. 39). Deutscher Alpenvereinsverlag, Munich 2004, ISBN 3-937530-06-1 (with numerous contributions on methodology).
Claus Roderich Mattmüller: On the orographic structure of mountains. In: Journal of Geomorphology. Vol. 55, No. 1, 2011, ISSN 0372-8854 , pp. 109-140, doi: 10.1127 / 0372-8854 / 2011 / 0055-0038 .

To mountains:

Adam Helman: The finest peaks. Prominence and other Mountain Measures . Trafford Publishing, Victoria 2005, ISBN 1-4120-5994-1 ( limited preview in Google Book Search).
Richard Goedeke : Top 20 in the Alps. The most important climbs on the most prominent mountains . Bruckmann, Munich 2008, ISBN 978-3-7654-4851-5 .

Web links

Prominence Theory (English)
Wolfgang Leonard: The high rise pages.de. Retrieved May 5, 2012 .

Notes and individual references

↑ Deviating from this, the notch height sometimes simply refers to the height of the notch above sea level and must then be distinguished from the prominence, cf. about independence of peaks , thehighrisepages.de

↑ "Scharte" stands for the mathematical saddle point , the point of a surface with a horizontal tangential plane and opposite curvatures, i.e. representative of all geomorphological and landscape forms of mountain passes , mountain saddles , yokes etc.

↑ Christian Thöni: How do you calculate the notch height of a mountain? www.gipfelverzeichnis.ch

↑ ^a ^b Klaus Hormann: About the morphographical structure of the earth's surface. In: Mitteilungen der Geographische Gesellschaft in München 50, 1965, pp. 109–126 (reference p. OA); also: ders .: Relative saddle and ramp length of the passes of Carinthia and East Tyrol. In: Mitt. D. Geogr. Ges. In Munich. Munich 1966.

↑ The Line Parent is sometimes referred to as Next or Nearest Neighbor Higher (see, for example.. (NHN) called Prominence Theory. In Lineage Theory: section 6. Peaklist.org. Accessed 17 October 2011 (English). ) . Other sources use the designation NHN for the actually closest higher mountain according to the dominance principle, cf. z. B. Peak excavators. Help and Glossary. In: Peakbagger.com. Retrieved October 17, 2011 .

↑ See e.g. B. Adam Helman: The Finest Peaks. Prominence and other Mountain Measures . Trafford Publishing, 2005, ISBN 1-4120-5995-X , pp. 83 ff . ( limited preview in Google Book search).

↑ If you allow sea level as a reference chart, the series ends last at Mount Everest.

↑ See Adam Helman: The Finest Peaks. Prominence and other Mountain Measures . Trafford Publishing, 2005, ISBN 1-4120-5995-X , pp. 85 ( limited preview in Google Book search).

↑ Prominence Theory. Section 6: Lineage Theory. Peaklist.org, accessed October 17, 2011 .

↑ ^a ^b ^c List of the most prominent mountains in the Alps

↑ Quoted from Stefan Rasemann: Geomorphometric structure of a mesoscale alpine geosystem . Dissertation Rheinische Friedrich-Wilhelms-Universität Bonn. Bonn 2003, 2.1.2 Definition and demarcation of the high mountains: Geomorphometric subdivision of high mountain systems - Table 2.4: Orders of magnitude of the mountain grouping based on the relative saddle for the semi-quantitative subdivision of high mountain systems (Hormann, 1965) , p. 41 ( hss.ulb.uni-bonn.de [PDF; 19.8 MB ; accessed on February 10, 2017]).

^ UIAA Documentation and Information Commission: The Four Thousand Mountains in the Alps - Official UIAA directory . In: UIAA bulletin . No. 145 , March 1994, p. 9 f . ( online [PDF; 630 kB ; accessed on May 15, 2008]).

^ ^A ^b Christian Thöni: Von Schartenhöhe and Dominanz . In: The Alps . No. 1/2003 , January 2003 ( PDF, 0.2MB ( memento of July 7, 2011 in the Internet Archive ) [accessed July 3, 2007]). About Schartenhöhe and Dominanz ( Memento of the original from July 7, 2011 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. @1@ 2
↑ ^a ^b Eberhard Jurgalski : Explanation of the dominance system. In: extreme-collect.de. Retrieved October 16, 2011 .
↑ thehighrisepages.de : independence of peaks .
^ The World Ultras Homepage. In: Peaklist.org. Retrieved October 17, 2011 .
↑ summit in Taunus , thehighrisepages.de

[1] Deviating from this, the notch height sometimes simply refers to the height of the notch above sea level and must then be distinguished from the prominence, cf. about independence of peaks , thehighrisepages.de

[2] "Scharte" stands for the mathematical saddle point , the point of a surface with a horizontal tangential plane and opposite curvatures, i.e. representative of all geomorphological and landscape forms of mountain passes , mountain saddles , yokes etc.

[Thöni_1-3] Christian Thöni: How do you calculate the notch height of a mountain? www.gipfelverzeichnis.ch

[Hormann-4] Klaus Hormann: About the morphographical structure of the earth's surface. In: Mitteilungen der Geographische Gesellschaft in München 50, 1965, pp. 109–126 (reference p. OA); also: ders .: Relative saddle and ramp length of the passes of Carinthia and East Tyrol. In: Mitt. D. Geogr. Ges. In Munich. Munich 1966.

[5] The Line Parent is sometimes referred to as Next or Nearest Neighbor Higher (see, for example.. (NHN) called Prominence Theory. In Lineage Theory: section 6. Peaklist.org. Accessed 17 October 2011 (English). ) . Other sources use the designation NHN for the actually closest higher mountain according to the dominance principle, cf. z. B. Peak excavators. Help and Glossary. In: Peakbagger.com. Retrieved October 17, 2011 .

[6] See e.g. B. Adam Helman: The Finest Peaks. Prominence and other Mountain Measures . Trafford Publishing, 2005, ISBN 1-4120-5995-X , pp. 83 ff . ( limited preview in Google Book search).

[7] If you allow sea level as a reference chart, the series ends last at Mount Everest.

[8] See Adam Helman: The Finest Peaks. Prominence and other Mountain Measures . Trafford Publishing, 2005, ISBN 1-4120-5995-X , pp. 85 ( limited preview in Google Book search).

[9] Prominence Theory. Section 6: Lineage Theory. Peaklist.org, accessed October 17, 2011 .

[Alps-10] List of the most prominent mountains in the Alps

[Rasemann_27-11] Quoted from Stefan Rasemann: Geomorphometric structure of a mesoscale alpine geosystem . Dissertation Rheinische Friedrich-Wilhelms-Universität Bonn. Bonn 2003, 2.1.2 Definition and demarcation of the high mountains: Geomorphometric subdivision of high mountain systems - Table 2.4: Orders of magnitude of the mountain grouping based on the relative saddle for the semi-quantitative subdivision of high mountain systems (Hormann, 1965) , p. 41 ( hss.ulb.uni-bonn.de [PDF; 19.8 MB ; accessed on February 10, 2017]).

[12] UIAA Documentation and Information Commission: The Four Thousand Mountains in the Alps - Official UIAA directory . In: UIAA bulletin . No. 145 , March 1994, p. 9 f . ( online [PDF; 630 kB ; accessed on May 15, 2008]).