Enzyme kinetics

The enzyme kinetics is a branch of biophysical chemistry . It describes how fast enzyme- catalyzed chemical reactions take place . Enzyme kinetics is widely used in biology and medicine , as biological substrates (reaction partners) - including those that occur in humans - are also examined. A main goal of enzyme kinetics is to describe the concentration dependency of the reaction rate with suitable formulas , as well as to determine the associated parameters for a specific protein ( enzyme activity and catalytic efficiency ). Since enzymes are used to speed up and direct reactions, enzyme kinetic analysis is essential to understanding enzyme functions.

Theory for enzymes with a substrate binding site

The first to describe the relationship between the substrate concentration and the rate of turnover of an enzyme was the French physical chemist Victor Henri in 1902. However, the importance of the hydrogen ion concentration for enzymatic reactions was not yet known at that time, only after Sørensen defined the pH value and the buffering in 1909 introduced, the German Leonor Michaelis and his Canadian post-doctoral student Maud Menten were able to experimentally confirm Henri's results in 1913. The Henri-Michaelis-Menten equation was generalized in 1925 by GE Briggs and JBS Haldane ( Michaelis-Menten theory ). ${\displaystyle [S]}$ ${\displaystyle v}$

Henri's key idea was to split the enzymatic reaction into two phases, the binding of the substrate S to the enzyme E and the conversion of the resulting enzyme-substrate complex ES into enzyme and product P:

${\displaystyle {\begin{aligned}E+S{\underset {k_{-1}}{\overset {k_{1}}{\begin{smallmatrix}\displaystyle \longrightarrow \\\displaystyle \longleftarrow \end{smallmatrix}}}}ES{\overset {k_{cat}}{\longrightarrow }}E+P\end{aligned}}}$ ${\displaystyle \quad }$(1)

Here are rate constants that are used in the kinetic derivation of the law of mass action (MWG) . To describe a reaction equilibrium of the binding reaction, the equality of the rates of the forward and reverse reaction has the form: ${\displaystyle k_{1},k_{-1},k_{cat}}$

${\displaystyle k_{1}[E][S]=k_{-1}[ES];\quad \mid :[ES]\quad \mid :k_{1}}$

where denotes the concentration of the substance . The stated mathematical operations result in the formulation of the MWG introduced for the binding reaction: ${\displaystyle \textstyle [X]}$ ${\displaystyle X}$

${\displaystyle {\frac {[E][S]}{[ES]}}={\frac {k_{-1}}{k_{1}}}=K_{\mathrm {d} }.\quad }$ (2)

Since the reaction products (noted in the numerator according to the standard) result from a dissociation of the enzyme-substrate complex, the equilibrium constant is known as the dissociation constant . ${\displaystyle \textstyle K_{\mathrm {d} }}$

As can be seen from equation (2), the dimension has a concentration. For the substrate concentration , half of all enzyme molecules are bound to the substrate, the other half is free; this is called half saturation of the enzyme. (The further reaction is initially disregarded.) ${\displaystyle \textstyle K_{\mathrm {d} }}$ ${\displaystyle \textstyle [S]=K_{\mathrm {d} }}$ ${\displaystyle \textstyle ES\longrightarrow E+P}$

Invoice for this

${\displaystyle K_{\mathrm {d} }={\frac {[E][S]}{[ES]}};\quad }$(2) Insertion of : ${\displaystyle K_{\mathrm {d} }=[S]\neq 0}$ ${\displaystyle [S]={\frac {[E][S]}{[ES]}};\quad \mid \cdot [ES]\quad \mid :[S]\neq 0}$ ${\displaystyle [ES]=[E]}$as claimed.

${\displaystyle \textstyle K_{\mathrm {d} }}$is inversely proportional to the affinity of the enzyme for the substrate: the better the enzyme binds the substrate, the lower the substrate concentration required for half-saturation of the enzyme.

To describe a reaction equilibrium of reaction (1) as a whole, the equality of the rates of the forward and reverse reaction has the form:

${\displaystyle k_{1}[E][S]=k_{-1}[ES]+k_{cat}[ES]=(k_{-1}+k_{cat})[ES];\quad \mid :[ES]\quad \mid :k_{1}}$

here is the rate constant of the reaction (assumed to be irreversible) . The mathematical operations given result in the formulation of the MWG introduced for reaction (1): ${\displaystyle k_{cat}}$ ${\displaystyle \textstyle ES\longrightarrow E+P}$

${\displaystyle {\frac {[E][S]}{[ES]}}={\frac {k_{-1}+k_{cat}}{k_{1}}}=K_{m}.\quad }$(3)

${\displaystyle K_{m}}$is called the Michaelis-Menten constant . To describe the reaction rate of the catalysis under consideration, it is further assumed (for appropriately suitable cases): ${\displaystyle v}$

• The concentration of the total enzyme present will not change and is the sum of the concentrations of substrate-bound and free enzyme, ie . ${\displaystyle [E]_{t}}$ ${\displaystyle [E]_{t}=[E]+[ES]}$
• The catalyzed reaction is first order , so that its speed is proportional to the concentration of the enzyme-substrate complex, ie . ${\displaystyle v=k_{cat}\cdot [ES]}$
• A maximum reaction speed is introduced as a calculation variable. This corresponds to the fictitious case that all of enzyme present as the enzyme-substrate complex is present, ie . ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle v_{\mathrm {max} }=k_{cat}\cdot [E]_{t}}$

By introducing these conditions, (3) can be converted into the Michaelis-Menten equation , which , depending on the substrate concentration, represents: ${\displaystyle v}$ ${\displaystyle [S]}$

${\displaystyle v={\frac {v_{\mathrm {max} }\cdot [S]}{K_{m}+[S]}}\quad }$

Reshaping

${\displaystyle {\frac {v}{v_{\mathrm {max} }}}={\frac {k_{cat}\cdot [ES]}{k_{cat}\cdot [E]_{t}}}={\frac {[ES]}{[E]_{t}}}={\frac {[ES]}{[E]+[ES]}};}$ to introduce the fraction, it is expanded with : ${\displaystyle \textstyle {\frac {[E][S]}{[ES]}}=K_{M}}$ ${\displaystyle \textstyle {[S] \over [ES]}}$ ${\displaystyle {\frac {v}{v_{\mathrm {max} }}}={\frac {[ES]}{[E]+[ES]}}={{[ES][S] \over [ES]} \over {[E][S] \over [ES]}+{[ES][S] \over [ES]}}\quad ={[S] \over K_{M}+[S]};\quad \mid \cdot v_{\mathrm {max} }}$ ${\displaystyle v={\frac {v_{\mathrm {max} }\cdot [S]}{K_{m}+[S]}};\quad }$Michaelis-Menten equation

The graph of this equation is part of a hyperbola that approaches the horizontal asymptote for increasing . ${\displaystyle [S]}$ ${\displaystyle v=v_{\mathrm {max} }}$

Calculation for the classification of the graph as part of a hyperbola; Consideration of the asymptotes

A. Since and are constants, is the function ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle K_{m}}$ ${\displaystyle v=f_{1}([S])={\frac {v_{\mathrm {max} }\cdot K_{m}}{[S]}};\quad [S]\in \mathbb {R} }$ a hyperbola with the horizontal asymptote for and the vertical asymptote for . ${\displaystyle v=0}$ ${\displaystyle [S]\to \pm \infty }$ ${\displaystyle [S]=0}$ ${\displaystyle [S]\to 0}$ Shift in -direction results in: ${\displaystyle -K_{m}}$ ${\displaystyle [S]}$ ${\displaystyle v=f_{2}([S])={\frac {v_{\mathrm {max} }\cdot K_{m}}{[S]-(-K_{m})}}={\frac {v_{\mathrm {max} }\cdot K_{m}}{K_{m}+[S]}}}$ (The following) reflection at the [S] axis results in: ${\displaystyle v=f_{3}([S])=-{\frac {v_{\mathrm {max} }\cdot K_{m}}{K_{m}+[S]}}}$ (Subsequent) shift in -direction results in: ${\displaystyle +v_{\mathrm {max} }}$ ${\displaystyle v}$ ${\displaystyle v=f_{4}([S])\quad =v_{\mathrm {max} }-{\frac {v_{\mathrm {max} }\cdot K_{m}}{K_{m}+[S]}}\quad =v_{\mathrm {max} }\cdot (1-{\frac {K_{m}}{K_{m}+[S]}})\quad =v_{\mathrm {max} }\cdot {\frac {K_{m}+[S]-K_{m}}{K_{m}+[S]}}\quad ={\frac {v_{\mathrm {max} }\cdot [S]}{K_{m}+[S]}};}$ since it is possible to generate congruence maps by chaining , there is also a hyperbola. The graph of the Michaelis-Menton equation is the subset of for which is. ${\displaystyle f_{4}([S])}$ ${\displaystyle f_{1}([S])}$ ${\displaystyle f_{4}([S])}$ ${\displaystyle f_{4}([S])}$ ${\displaystyle [S]\geq 0}$ B. The first two congruence maps mentioned above do not change the horizontal asymptote of the hyperbola, the latter shifts it in the direction. So the asymptote for ; the graph of the Michaelis-Menton equation contained in strives for against this asymptote. ${\displaystyle +v_{\mathrm {max} }}$ ${\displaystyle v}$ ${\displaystyle f_{4}([S])}$ ${\displaystyle v=v_{\mathrm {max} }}$ ${\displaystyle [S]\to \pm \infty }$ ${\displaystyle f_{4}([S])}$ ${\displaystyle [S]\to +\infty }$ The first-mentioned congruence map shifts the vertical asymptote of the hyperbola in -direction, the latter two do not change anything about it. So has the asymptote for . ${\displaystyle -K_{M}}$ ${\displaystyle v}$ ${\displaystyle f_{4}([S])}$ ${\displaystyle [S]=-K_{M}}$ ${\displaystyle [S]\to -K_{M}}$

As can be seen from equation (3), the dimension also has a concentration. For the substrate concentration is . ${\displaystyle \textstyle K_{m}}$ ${\displaystyle \textstyle [S]=K_{m}}$ ${\displaystyle \textstyle v={\frac {v_{\mathrm {max} }}{2}}}$

Invoice for this

Substituting into the Michaelis-Menton equation: ${\displaystyle K_{m}=[S]}$ ${\displaystyle \ v={v_{\mathrm {max} }\cdot [S] \over [S]+[S]}={v_{\mathrm {max} }\cdot [S] \over 2\cdot [S]}={\frac {v_{\mathrm {max} }}{2}}}$.

For the determination of and out series of measurements of and computer-based methods such as non-linear serve regression analysis ( simplex or Levenberg-Marquardt method ). Graphic extrapolation methods (linearizations) such as the double-reciprocal application according to Lineweaver and Burk should not be used for this, as they are too imprecise. However, it is very suitable for presenting the results of enzyme kinetic experiments. ${\displaystyle v_{\text{max}}}$ ${\displaystyle K_{m}}$ ${\displaystyle v}$ ${\displaystyle [S]}$

Theory for enzymes with multiple substrate binding sites

The Hill equation and its derivation from the law of mass action

The Hill equation was originally introduced by Archibald Vivian Hill to mathematically describe the oxygen binding to hemoglobin as a function of various oxygen concentrations. The Hill equation described here is different from the Hill equation describing muscle contraction, which the same author helped create.

Although the binding of oxygen to hemoglobin is not a catalytic process, a Hill equation can also be used to describe the kinetics of enzymatic catalysis, especially those whose kinetics cannot be described with a Michaelis-Menten equation. Here follows a derivation of the Hill equation from the law of mass action, which emphasizes the analogy to the derivation of the Michaelis-Menten equation. Correspondingly, the variable means the number of binding sites that a molecule of enzyme holds ready for each molecule of substrate, and is therefore a positive natural number . The values ​​found experimentally deviate from this (see below "The empirical Hill coefficient as a measure of the cooperativity of enzymes"). ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n_{H}}$

The binding of substrate molecules to an enzyme can be modeled with: ${\displaystyle n}$

${\displaystyle {\begin{aligned}E+nS{\underset {k_{-1}'}{\overset {k_{1}'}{\begin{smallmatrix}\displaystyle \longrightarrow \\\displaystyle \longleftarrow \end{smallmatrix}}}}ES_{n}\end{aligned}}}$ ${\displaystyle \quad }$(1')

As in equation (1) are rate constants that are used in the kinetic derivation of the law of mass action (MWG) . To describe a reaction equilibrium of the binding reaction, the equality of the rates of the forward and reverse reaction has the form: ${\displaystyle k_{1}',k_{-1}'}$

${\displaystyle k_{1}'[E][S]^{n}=k_{-1}'[ES_{n}];\quad \mid :[ES_{n}]\quad \mid :k_{1}'\quad }$

here is the concentration of free enzyme, the substrate concentration, the concentration of the enzyme-substrate complexes with molecules of the substrate. The exponent is called the Hill coefficient . The stated mathematical operations result in the formulation of the MWG introduced for the binding reaction: ${\displaystyle [E]}$ ${\displaystyle [S]}$ ${\displaystyle [ES_{n}]}$ ${\displaystyle n}$ ${\displaystyle n}$

${\displaystyle {\frac {[E][S]^{n}}{[ES_{n}]}}={k_{-1}' \over k_{1}'}=K_{\mathrm {D} }.\quad }$ (2 ')

Analogous to the dissociation constant in equation (2) is called the apparent dissociation constant . The adjective "apparently" takes into account the fact that the experimentally measured values ​​for differ from those to be expected according to this model. ${\displaystyle K_{d}}$ ${\displaystyle K_{D}}$ ${\displaystyle n}$

As can be seen from equation (2 '), the constant (to be introduced) has

${\displaystyle K_{A}=K{_{\mathrm {D} }}^{1 \over n}\Leftrightarrow K{_{A}}^{n}=K_{\mathrm {D} }\quad }$(3 ')

the dimension of a concentration. For the substrate concentration , half of all enzyme molecules are bound to the substrate, the other half is free; this is called half saturation of the enzyme. ${\displaystyle \textstyle [S]=K_{A}}$

invoice

Equating equations (2 ') and (3') gives: ${\displaystyle {\frac {[E][S]^{n}}{[ES_{n}]}}=\quad K_{\mathrm {D} }=\quad K{_{A}}^{n}\quad }$ Insertion of : ${\displaystyle K_{A}=[S]}$ ${\displaystyle [S]^{n}={\frac {[E][S]^{n}}{[ES_{n}]}};\quad \mid \cdot [ES_{n}]\quad \mid :[S]^{n}\neq 0}$ ${\displaystyle [ES_{n}]=[E]}$as claimed.

${\displaystyle \textstyle K_{A}}$is therefore referred to as the half-saturation constant and also written (for "50%"). is (like the constant of the Michaelis-Menten equation) inversely proportional to the affinity of the enzyme for the substrate: the better the enzyme binds the substrate, the lower the substrate concentration required for half-saturation of the enzyme. ${\displaystyle \textstyle K_{50}}$ ${\displaystyle K_{A}}$ ${\displaystyle \textstyle K_{\mathrm {d} }}$

If it is further assumed

• that the concentration of the total enzyme present does not change and that the sum of the concentrations of substrate-bound and free enzyme is, i.e. , ${\displaystyle [E]_{t}}$ ${\displaystyle [E]_{t}=[E]+[ES_{n}]}$

then the proportion of substrate-bound enzyme in the total available with equation (2 ') is: ${\displaystyle \theta }$

${\displaystyle \theta ={[ES_{n}] \over [E]_{t}}={[S]^{n} \over K_{D}+[S]^{n}};\quad }$Hill equation

invoice

${\displaystyle \theta ={[ES_{n}] \over [E]_{t}}={[ES_{n}] \over [E]+[ES_{n}]};}$ to introduce the fraction, it is expanded with : ${\displaystyle \textstyle {\frac {[E][S]^{n}}{[ES_{n}]}}=K_{\mathrm {D} }}$ ${\displaystyle \textstyle {[S]^{n} \over [ES_{n}]}}$ ${\displaystyle \theta ={[ES_{n}] \over [E]+[ES_{n}]}={{[ES_{n}][S]^{n} \over [ES_{n}]} \over {[E][S]^{n} \over [ES_{n}]}+{[ES_{n}][S]^{n} \over [ES_{n}]}}\quad ={[S]^{n} \over K_{\mathrm {D} }+[S]^{n}};\quad }$Hill equation

In order to use the Hill equation to describe the rate of reaction of catalysis by an enzyme with several binding sites, it is sufficient to further assume: ${\displaystyle v}$

• A maximum reaction speed is introduced as a calculation variable. This corresponds to the fictitious case that all of enzyme present as the enzyme-substrate complex is present, ie . ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle \theta =1}$
• ${\displaystyle v\leq v_{\mathrm {max} }}$is proportional to the amount of substrate-bound enzyme in the total available. ${\displaystyle \theta }$

Then the proportionality has the form

${\displaystyle {\frac {v}{v_{\mathrm {max} }}}=\theta ;\quad }$(4)

invoice

Because of the assumed proportionality of and to, there is a proportionality factor such that: ${\displaystyle v}$ ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle \theta }$ ${\displaystyle k}$ ${\displaystyle v=k\cdot \theta \quad }$ and ${\displaystyle \quad v_{\mathrm {max} }=k\cdot 1}$ So the ratio of to : ${\displaystyle v}$ ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle {\frac {v}{v_{\mathrm {max} }}}={k\cdot \theta \over k\cdot 1}=\theta \quad }$(4)

Equating with the Hill equation results in an equation which, as a function of the -th power of the substrate concentration, is: ${\displaystyle v}$ ${\displaystyle n}$ ${\displaystyle [S]^{n}}$

${\displaystyle v={v_{\mathrm {max} }\cdot [S]^{n} \over K_{D}+[S]^{n}};\quad }$ (5)

invoice

Equating equation (4) with the Hill equation gives: ${\displaystyle {\frac {v}{v_{\mathrm {max} }}}=\theta ={[S]^{n} \over K_{D}+[S]^{n}};\quad \mid \cdot v_{\mathrm {max} }}$ ${\displaystyle v={v_{\mathrm {max} }\cdot [S]^{n} \over K_{D}+[S]^{n}}\quad }$ (5)

The derivation of equation (5) is largely analogous to the derivation of the Michaelis-Menten equation. The differences are:

• The rate constant of the catalyzed reaction is not included in the derivation of equation (5): unlike formally, does not depend on. ${\displaystyle k_{cat}}$ ${\displaystyle K_{D}}$ ${\displaystyle K_{M}}$ ${\displaystyle k_{cat}}$
• The order of the catalyzed reaction is not explicitly considered in the derivation of (5).

Instead of the last two conditions mentioned, the proportionality formulated in equation (4) is used in the derivation; an abstract proportionality factor takes the place of . ${\displaystyle k}$ ${\displaystyle k_{cat}}$

Further representation for and for . The saturation function ${\displaystyle \theta }$ ${\displaystyle v}$

In the Hill equation is by and dependent, but even also (see equation (2 ')). The behavior of the equation as a function of can be represented more uniformly (see below graphs plotted in semi-logarithms) if is replaced by: ${\displaystyle \theta }$ ${\displaystyle n}$ ${\displaystyle K_{D}}$ ${\displaystyle K_{D}}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle K_{D}}$ ${\displaystyle K_{A}}$

${\displaystyle \theta ={[S]^{n} \over K_{D}+[S]^{n}}={1 \over 1+({K_{A} \over [S]})^{n}};\quad }$ (6)

Reshaping

Inserting (3 '): into the Hill equation gives: ${\displaystyle K{_{A}}^{n}=K_{\mathrm {D} }}$ ${\displaystyle \theta ={[S]^{n} \over [S]^{n}+K{_{A}}^{n}};\quad }$expand with and shorten in numerator and denominator: ${\displaystyle \textstyle {1 \over [S]^{n}}}$ ${\displaystyle \textstyle {[S]^{n} \over [S]^{n}}}$ ${\displaystyle \theta ={1 \over 1+({K_{A} \over [S]})^{n}};\quad }$ (6)

Equating equations (4) and (6) results in a representation of , which also no longer contains: ${\displaystyle v}$ ${\displaystyle K_{D}}$

${\displaystyle v={v_{\mathrm {max} } \over 1+({K_{A} \over [S]})^{n}};\quad }$ (7)

invoice

Equating equations (4) and (6) gives: ${\displaystyle {v \over v_{\mathrm {max} }}=\theta ={1 \over 1+({K_{A} \over [S]})^{n}};\quad \mid \cdot v_{\mathrm {max} }}$ ${\displaystyle v={v_{\mathrm {max} } \over 1+({K_{A} \over [S]})^{n}};\quad }$ (7)

If substrate is bound to a molecule of enzyme molecules and the concentration of the enzyme-substrate complex is, then is the concentration of the bound substrate . The ratio of the concentration of bound substrate to the concentration of the total enzyme present is called the saturation function: ${\displaystyle n}$ ${\displaystyle [ES_{n}]}$ ${\displaystyle n\cdot [ES_{n}]}$ ${\displaystyle r}$

${\displaystyle r={n\cdot [ES_{n}] \over [E]_{t}}}$

The relationship to the Hill equation is given because of ${\displaystyle \textstyle \theta ={[ES_{n}] \over [E]_{t}}}$

${\displaystyle r=n\cdot \theta .\quad }$ (8th)

The empirical Hill coefficient as a measure of the cooperativity of enzymes ${\displaystyle n_{H}}$

According to the derivation of the Hill equation from the law of mass action (see above), the Hill coefficient is the number of binding sites of an enzyme and therefore a natural number. (Exactly) for are the constants and equal. Equations (5) and (7) are also exactly equivalent to a Michaelis-Menten equation in that the constant is understood as a Michaelis-Menten constant . ${\displaystyle \textstyle n}$ ${\displaystyle \textstyle n=1}$ ${\displaystyle \textstyle K_{D}}$ ${\displaystyle \textstyle K_{A}=K{_{D}}^{1 \over n}}$ ${\displaystyle n=1}$ ${\displaystyle \textstyle K_{D}=K_{A}}$ ${\displaystyle \textstyle K_{M}}$

Calculation for equation (7)

${\displaystyle v={v_{\mathrm {max} } \over 1+({K_{A} \over [S]})^{n}};\quad }$ (7) ${\displaystyle n=1}$insert and expand with : ${\displaystyle [S]}$ ${\displaystyle v={v_{\mathrm {max} }\cdot [S] \over [S]+{K_{A}\cdot [S] \over [S]}};}$ with : ${\displaystyle K_{A}=K_{M}}$ ${\displaystyle v={v_{\mathrm {max} }\cdot [S] \over [S]+K_{M}};\quad }$ Michaelis-Menten equation

To distinguish it from , the variable denotes the Hill coefficient for which the Hill equation empirically best describes the kinetics of such an enzyme. is usually less than and not a natural number. The theory of the Hill equation is only mathematically consistent when using is replaced by in all equations used to describe the kinetics . (9) ${\displaystyle n}$ ${\displaystyle n_{H}}$ ${\displaystyle n_{H}}$ ${\displaystyle n}$ ${\displaystyle n_{H}}$ ${\displaystyle n}$ ${\displaystyle n_{H}}$ ${\displaystyle \quad \quad }$

In the following, the constants and in all situations to be compared of the enzymes under consideration are the same. The difference between and is explained by the fact that enzymes with several substrate binding sites consist of several subunits, each of which has a binding site and can therefore be described in isolation with a Michaelis-Menten equation. ${\displaystyle K_{A}}$ ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle \mathrm {-} }$ ${\displaystyle n_{H}}$ ${\displaystyle n}$ ${\displaystyle n_{H}=1}$

An interaction of the subunits referred to as positive cooperativity can, however, also have the effect that such an enzyme reacts faster at a given substrate concentration than would be expected according to a Michaelis-Menten equation . A Hill equation describes positive cooperativity for concentrations if and only if is. Furthermore, in the case of positive cooperativity at a given substrate concentration, an enzyme reacts faster the larger it is. Logical upper limit for is (the number of binding sites) . ${\displaystyle [S]}$ ${\displaystyle K_{M}=K_{A}}$ ${\displaystyle [S]>K_{A}}$ ${\displaystyle n_{H}>1}$ ${\displaystyle [S]>K_{A}}$ ${\displaystyle n_{H}}$ ${\displaystyle n_{H}}$ ${\displaystyle n}$

Correspondingly, an interaction of subunits of an enzyme called negative cooperativity can cause the enzyme to react more slowly at a given substrate concentration than would be expected according to a Michaelis-Menten equation . A Hill equation describes negative cooperativity for concentrations if and only if is, and at a given substrate concentration an enzyme reacts slower with negative cooperativity, the smaller it is. ${\displaystyle [S]}$ ${\displaystyle K_{M}=K_{A}}$ ${\displaystyle [S]>K_{A}}$ ${\displaystyle n_{H}<1}$ ${\displaystyle [S]>K_{A}}$ ${\displaystyle n_{H}}$

proof

The following inequality (i) uses equation (7) to calculate the velocities of two enzymes whose situations only differ in the Hill coefficient or . The following equivalence transformations (i) are based on the conditions mentioned in the text. ${\displaystyle n_{H}}$ ${\displaystyle n{_{H}}'}$ ${\displaystyle {v_{\mathrm {max} } \over 1+({K_{A} \over [S]})^{n_{H}}}>{v_{\mathrm {max} } \over 1+({K_{A} \over [S]})^{n{_{H}}'}};\quad }$(i) The substitution is used for a clearer notation . After (necessary) additional requirements apply ${\displaystyle \textstyle q:={K_{A} \over [S]}}$ ${\displaystyle [S]>K_{A}\quad \mid :[S]>0\Rightarrow }$ ${\displaystyle 1>{K_{A} \over [S]}=q>0,\quad }$ (ii) because for the consideration can be presupposed. Insertion gives: ${\displaystyle K_{A},[S]>0}$ ${\displaystyle {v_{\mathrm {max} } \over 1+q^{n_{H}}}>{v_{\mathrm {max} } \over 1+q^{n{_{H}}'}};\quad \mid :v_{\mathrm {max} }>0}$ ${\displaystyle {1 \over 1+q^{n_{H}}}>{1 \over 1+q^{n{_{H}}'}};\quad \mid }$plunge positive fractions ${\displaystyle 1+q^{n_{H}}<1+q^{n{_{H}}'};\quad \quad \mid -1\quad \mid :q^{n{_{H}}'}>0}$ ${\displaystyle q^{n_{H}-n{_{H}}'}<1;\quad \quad \quad \quad \mid \log }$on a selectable basis ; with the calculation rule for the logarithm of a power : ${\displaystyle (n_{H}-n{_{H}}')\cdot \log {q}<0;\quad \mid :\log {q}<0}$because of (ii) ${\displaystyle 0<q<1}$ ${\displaystyle n_{H}-n{_{H}}'>0\quad \Leftrightarrow \quad n_{H}>n{_{H}}'}$ For the right side of (i) the function term is equivalent to a Michaelis-Menten equation (see above "Calculation for equation (7)"). Hence, consideration of shows that in a Hill equation for describes positive cooperativity as claimed. ${\displaystyle n{_{H}}'=1}$ ${\displaystyle n{_{H}}'=1}$ ${\displaystyle n_{H}>1}$ ${\displaystyle [S]>K_{A}}$ Consideration of arbitrary pairs shows that of two (comparable) enzymes that show positive cooperativity, the one with the larger Hill coefficient reacts faster, as claimed. ${\displaystyle n_{H}>n{_{H}}'>1}$ ${\displaystyle [S]>K_{A}}$ For the left side of (i) the functional term is equivalent to a Michaelis-Menten equation (see above "Calculation for equation (7)"). Hence, consideration of shows that in a Hill equation describes negative cooperativity as claimed. ${\displaystyle n_{H}=1}$ ${\displaystyle n_{H}=1}$ ${\displaystyle n{_{H}}'<1}$ ${\displaystyle [S]>K_{A}}$ Consideration of arbitrary pairs shows that of two (comparable) enzymes that show negative cooperativity, the one with the smaller Hill coefficient reacts more slowly, as claimed. ${\displaystyle 1>n_{H}>n{_{H}}'}$ ${\displaystyle [S]>K_{A}}$

An enzyme with several binding sites in which such an interaction of the subunits cannot be observed is not called cooperative .

Cooperativity is described not only for enzymes, but also for non-enzyme proteins to which several other molecules bind (see derivation of the Hill equation above). A Hill coefficient of 2.8 was determined for the coordinative binding of oxygen to hemoglobin , which consists of one oxygen molecule binding subunits . ${\displaystyle n=4}$ ${\displaystyle n_{H}}$

Calculation of ${\displaystyle n_{H}}$

If the substrate concentrations or known at which an enzyme reacts at 10% or 90% of its maximum speed , its empirical Hill coefficient can be determined: ${\displaystyle [S]=\mathrm {EC_{10}} }$ ${\displaystyle [S]=\mathrm {EC_{90}} }$ ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle n_{H}}$

${\displaystyle n_{H}=\mathrm {\frac {\log(81)}{\log(EC_{90}/EC_{10})}} }$

Generalization: If any two different substrate concentrations or are known at which an enzyme reacts with 0% <P% <100% or 0% <Q% <100% of its maximum speed , then its empirical Hill coefficient is given by the following quotient : ${\displaystyle EC_{P}}$ ${\displaystyle EC_{Q}}$ ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle n_{H}}$

${\displaystyle n_{H}={\bigg (}\log {\Big (}{100\cdot P-P\cdot Q \over 100\cdot Q-P\cdot Q}{\Big )}{\bigg )}:{\bigg (}\log {\Big (}{EC_{P} \over EC_{Q}}{\Big )}{\bigg )}}$

Derivation

A. With consideration (9), when considering the empirical Hill coefficient in equation (6) , replace with. The following transformations solve the resulting equation for: ${\displaystyle n}$ ${\displaystyle n_{H}}$ ${\displaystyle [S]^{n_{H}}}$ ${\displaystyle \theta ={1 \over 1+({K_{A} \over [S]})^{n_{H}}};\quad \quad \mid }$Transition to the reciprocal number ${\displaystyle \quad \mid -1}$ ${\displaystyle {1 \over \theta }-1={1-\theta \over \theta }={{K_{A}}^{n_{H}} \over [S]^{n_{H}}};\quad \mid }$Ruptures ${\displaystyle \quad \mid \cdot {K_{A}}^{n_{H}}}$ ${\displaystyle {{K_{A}}^{n_{H}}\cdot \theta \over 1-\theta }=[S]^{n_{H}};\quad }$(i) B. With equation (4): ${\displaystyle {\frac {v}{v_{\mathrm {max} }}}=\theta ;}$ is given not only by the Hill equation but also by the proportion of the measured reaction speed in the maximum speed ; this proportion can be expressed as a percentage or as a decimal number. - Inserting for or of for in (i) results in: ${\displaystyle \theta }$ ${\displaystyle v}$ ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle \theta =90\%=0{,}9}$ ${\displaystyle [S]=\mathrm {EC_{90}} }$ ${\displaystyle \theta =10\%=0{,}1}$ ${\displaystyle [S]=\mathrm {EC_{10}} }$ ${\displaystyle {{K_{A}}^{n_{H}}\cdot 0{,}9 \over 1-0{,}9}={K_{A}}^{n_{H}}\cdot 9=\mathrm {EC_{90}} ^{n_{H}}\quad }$(ii) ${\displaystyle {{K_{A}}^{n_{H}}\cdot 0{,}1 \over 1-0{,}1}={{K_{A}}^{n_{H}}\cdot {1 \over 9}}=\mathrm {EC_{10}} ^{n_{H}}\quad }$(iii) C. (ii) and (iii) give the proportionality : ${\displaystyle {\Big (}{\mathrm {EC_{90}} \over \mathrm {EC_{10}} }{\Big )}^{n_{H}}={\mathrm {EC_{90}} ^{n_{H}} \over \mathrm {EC_{10}} ^{n_{H}}}={{K_{A}}^{n_{H}}\cdot 9 \over {{K_{A}}^{n_{H}}\cdot {1 \over 9}}}=81;}$ With a logarithm to a selectable base and the calculation rule for the logarithm of a power : ${\displaystyle n_{H}\cdot \log {\Big (}{\mathrm {EC_{90}} \over \mathrm {EC_{10}} }{\Big )}=\log 81;\quad \mid :\log {\Big (}{\mathrm {EC_{90}} \over \mathrm {EC_{10}} }{\Big )}>0,\quad }$there ${\displaystyle \mathrm {EC_{90}} >\mathrm {EC_{10}} }$ ${\displaystyle n_{H}={\log 81 \over \log {\Big (}{\mathrm {EC_{90}} \over \mathrm {EC_{10}} }{\Big )}},\quad }$ as stated. D. Generalization: For any two different proportions or of and the associated substrate concentrations or the same calculation method results: ${\displaystyle 0<p<1}$ ${\displaystyle 0<q<1}$ ${\displaystyle \theta }$ ${\displaystyle [S]=EC_{P=100p}}$ ${\displaystyle [S]=EC_{Q=100q}}$ ${\displaystyle {{K_{A}}^{n_{H}}\cdot p \over 1-p}={EC_{P}}^{n_{H}}\quad }$(ii ') ${\displaystyle {{K_{A}}^{n_{H}}\cdot q \over 1-q}={EC_{Q}}^{n_{H}}\quad }$(iii ') ${\displaystyle n_{H}\cdot \log {\Big (}{EC_{P} \over EC_{Q}}{\Big )}=\log {{{K_{A}}^{n_{H}}\cdot p \over 1-p} \over {{K_{A}}^{n_{H}}\cdot q \over 1-q}}=\log {\Big (}{p(1-q) \over (1-p)q}{\Big )}=\log {\Big (}{p-pq \over q-pq}{\Big )}=\log {\Big (}{100\cdot P-P\cdot Q \over 100\cdot Q-P\cdot Q}{\Big )},}$ where the fraction was expanded in the last step ; with division by the factor (different from zero after construction) the given formula follows. ${\displaystyle 100^{2}}$ ${\displaystyle \textstyle \log {\Big (}{EC_{P} \over EC_{Q}}{\Big )}}$

Non-linearized graphs

Direct linear plot of enzyme kinetics according to Michaelis-Menten

Direct linear application

Enzyme kinetic parameters can be conveniently and precisely derived directly from a saturation hyperbola as shown in the figure (“direct-linear plot” also called “Cornish-Bowden diagram”). In this hyperbola, the enzymatic turnover rate ( ordinate ) is shown as a function of the substrate concentration ( abscissa ). ${\displaystyle v}$ ${\displaystyle [S]}$

For the direct linear plot, the initial rates of the enzymatic conversion are transferred directly to the - diagram. The values ​​are known before the start of the experiment (set substrate concentrations); The ordinate value for (the initial speed) must then be entered during the test series . Half of the maximum turnover rate can be derived from the maximum turnover rate . The coordinate value for can be determined graphically from this . The catalytic efficiency , incidentally, follows from the slope of the tangent to the origin: ; from this it follows . ${\displaystyle v}$ ${\displaystyle [S]}$ ${\displaystyle [S]}$ ${\displaystyle v}$ ${\displaystyle v_{\text{max}}}$ ${\displaystyle {\tfrac {1}{2}}v_{\text{max}}}$ ${\displaystyle K_{m}}$ ${\displaystyle {\tfrac {v_{\text{max}}}{K_{m}}}}$ ${\displaystyle {\tfrac {k_{cat}}{K_{m}}}}$

Calculation of the slope of the tangent to the origin

The functional equation of the hyperbola is the Michaelis-Menten equation ${\displaystyle v([S])=\quad {\frac {v_{\mathrm {max} }[S]}{K_{\mathrm {m} }+[S]}};}$ the slope of the tangent to the origin can be understood as the limit value of a secant slope , which is given by a difference quotient . When approached from the right, this results in : ${\displaystyle m_{t}}$ ${\displaystyle m_{t}=\lim _{h\rightarrow 0,\,h>0}{\frac {v(0+h)-v(0)}{h}}=\quad }$ ${\displaystyle \lim _{h\rightarrow 0,\,h>0}{v(h)-0 \over h}=\quad }$ ${\displaystyle \lim _{h\rightarrow 0,\,h>0}{\frac {v_{\mathrm {max} }h}{(K_{\mathrm {m} }+h)\cdot h}}=\quad }$ ${\displaystyle {\frac {v_{\mathrm {max} }}{K_{\mathrm {m} }}}.}$ Note : The standard way of deriving the function according to the quotient rule requires additional considerations because of the only one-sided differentiability of at this point and is also more computationally expensive. ${\displaystyle v([S])}$ ${\displaystyle v([S])}$ ${\displaystyle [S]=0}$

Error handling is largely simplified in the direct linear plot: averaging then gives the probable values ​​for the parameters and . When inspecting the spread of the measuring points (not identical to their standard deviation ), outliers can easily be identified and so-called medians can be read off. ${\displaystyle K_{m}}$ ${\displaystyle v_{\text{max}}}$

At this point it should be mentioned that all (including the following) evaluation methods are not only valid for enzymes but also for the binding processes of carriers or receptors. Historically, all of these methods (Hanes and Eadie-Hofstee plots for enzymes, Scatchard and Hill plots for carriers) were originally developed by Woolf.

Direct linear plotted graphs of enzyme kinetics according to Hill for different values ​​of ${\displaystyle n_{H}}$

Equation (5) derived from the Hill equation can be interpreted as a function which describes the empirically found reaction rate as a function of the substrate concentration . After consideration (9) of the function is in the formulation by replacing to: ${\displaystyle v}$ ${\displaystyle [S]}$ ${\displaystyle n}$ ${\displaystyle n_{H}}$

${\displaystyle f([S])=v={v_{\mathrm {max} }\cdot [S]^{n_{H}} \over K_{D}+[S]^{n_{H}}}.}$

f ([S]) is strictly monotonically increasing everywhere and approaches the horizontal asymptote for increasing . The graph of f ([S]) shows different behavior depending on the value : ${\displaystyle [S]}$ ${\displaystyle v=v_{\mathrm {max} }}$ ${\displaystyle n_{H}}$

• For it is part of a hyperbola, since equation (5) is then equivalent to a Michaelis-Menten equation (see above). ${\displaystyle n_{H}=1}$
• For he has exactly one turning point at . Taking into account its slope behavior, there is therefore a sigmoid function in this case . The case is distinguishable from the cases and differ by mere observation of the graph. ${\displaystyle n_{H}>1}$ ${\displaystyle \textstyle [S]_{w}={\Big (}K_{D}\cdot {n_{H}-1 \over n_{H}+1}{\Big )}^{1 \over n_{H}}=K_{A}\cdot {\Big (}{n_{H}-1 \over n_{H}+1}{\Big )}^{1 \over n_{H}}}$ ${\displaystyle f([S])}$ ${\displaystyle n_{H}>1}$ ${\displaystyle n_{H}=1}$ ${\displaystyle n_{H}<1}$
• For it has no turning point and looks like part of a hyperbola. Such a graph is called pseudohyperbolic because the case cannot be distinguished from the case simply by looking at the graph. ${\displaystyle n_{H}<1}$ ${\displaystyle n_{H}<1}$ ${\displaystyle n_{H}=1}$

Mathematical evidence

Preliminary considerations: For the problem presented, (as a definition of ) and can be assumed. (i) ${\displaystyle [S]\geq 0}$ ${\displaystyle f([S])}$ ${\displaystyle v_{\mathrm {max} },K_{D},n_{H}>0}$ For any are power functions strictly , and their values run through for all positive real numbers. (ii) ${\displaystyle 0\neq a\in \mathbb {R} }$ ${\displaystyle [S]\rightarrow [S]^{a}}$ ${\displaystyle [S]>0}$ For any are for the powers . (iii) ${\displaystyle n_{H}\in \mathbb {R} }$ ${\displaystyle K_{D},[S]>0}$ ${\displaystyle [S]^{n_{H}},[S]^{n_{H}-1},[S]^{n_{H}-2},(K_{D}+[S]^{n_{H}})^{2},(K_{D}+[S]^{n_{H}})^{3}>0}$ A. For any , the convergence of the power function yields : ${\displaystyle n_{H}>0\Leftrightarrow -n_{H}<0}$ ${\displaystyle \lim _{[S]\to \infty }{K_{D} \over [S]^{n_{H}}}=K_{D}\cdot \lim _{[S]\to \infty }[S]^{-n_{H}}=K_{D}\cdot 0=0;\quad }$from this follows for the function term from to expand by : ${\displaystyle \textstyle f([S])}$ ${\displaystyle \textstyle {1 \over [S]^{n_{H}}}}$ ${\displaystyle \lim _{[S]\to \infty }{v_{\mathrm {max} }\cdot [S]^{n_{H}} \over K_{D}+[S]^{n_{H}}}=\lim _{[S]\to \infty }{v_{\mathrm {max} }\cdot {[S]^{n_{H}} \over [S]^{n_{H}}} \over {K_{D} \over [S]^{n_{H}}}+{[S]^{n_{H}} \over [S]^{n_{H}}}}={v_{\mathrm {max} }\cdot 1 \over 0+1}=v_{\mathrm {max} },\quad }$ as claimed. B. The derivative ${\displaystyle f'([S])={v_{\mathrm {max} }\cdot K_{D}\cdot n_{H}\cdot [S]^{n_{H}-1} \over (K_{D}+[S]^{n_{H}})^{2}}}$ is positive for everywhere with (i) and (iii) , so that increases strictly monotonically for all . Additional consideration of and shows that in the entire domain of definition increases strictly monotonically, as claimed. ${\displaystyle [S]>0}$ ${\displaystyle f([S])}$ ${\displaystyle [S]>0}$ ${\displaystyle f(0)=0}$ ${\displaystyle f([S]>0)>0}$ ${\displaystyle f([S])}$ C. The turning points of are exactly the zeros with a change in sign of the second derivative ${\displaystyle f([S])}$ ${\displaystyle f''([S])=v_{\mathrm {max} }\cdot K_{D}\cdot n_{H}\cdot [S]^{n_{H}-2}\cdot {K_{D}(n_{H}-1)-[S]^{n{_{H}}}(n_{H}+1) \over (K_{D}+[S]^{n_{H}})^{3}}=a([S])\cdot {b([S]) \over c([S])},\quad }$where the following applies to the auxiliary functions : ${\displaystyle a([S]),b([S]),c([S])}$ ${\displaystyle a([S])=v_{\mathrm {max} }\cdot K_{D}\cdot n_{H}\cdot [S]^{n_{H}-2}>0\quad }$for after (i) and (iii); ${\displaystyle \quad [S]>0\quad }$ ${\displaystyle b([S])=K_{D}(n_{H}-1)-[S]^{n{_{H}}}(n_{H}+1)}$; ${\displaystyle c([S])=(K_{D}+[S]^{n_{H}})^{3}>0\quad }$for after (iii). ${\displaystyle \quad [S]>0\quad }$ Since for is not defined, in does not change the sign and has no turning point at. Except for all turning points: ${\displaystyle f''([S])}$ ${\displaystyle [S]<0}$ ${\displaystyle f''([S])}$ ${\displaystyle [S]=0}$ ${\displaystyle f([S])}$ ${\displaystyle [S]=0}$ ${\displaystyle [S]>0}$ ${\displaystyle f''([S])=0\quad \Leftrightarrow \quad b([S])=0\quad \Leftrightarrow \quad [S]^{n_{H}}=K_{D}\cdot {n_{H}-1 \over n_{H}+1}=:D.\quad }$ (iv) With (ii), equation (iv) has a solution if and only if is and then exactly one (i.e. its solution is unique if it exists). ${\displaystyle D>0}$ ${\displaystyle [S]=[S]_{w}}$ Mit is for such that no solution of (iv) exists and has no inflection point as claimed. ${\displaystyle K_{D}>0}$ ${\displaystyle D<0}$ ${\displaystyle n_{H}<1}$ ${\displaystyle f([S])}$ With is for , so then exactly one solution ${\displaystyle K_{D}>0}$ ${\displaystyle D>0}$ ${\displaystyle n_{H}>1}$ ${\displaystyle [S]_{w}=D^{1 \over n_{H}}={\Big (}K_{D}\cdot {n_{H}-1 \over n_{H}+1}{\Big )}^{1 \over n_{H}}=K_{A}\cdot {\Big (}{n_{H}-1 \over n_{H}+1}{\Big )}^{1 \over n_{H}}}$ of equation (iv) exists; has at most one turning point in (ii) . To show is that in changes sign. Since the determination of the third derivative is quite complex, the behavior of in the vicinity of its zeros is examined here. ${\displaystyle f([S])}$ ${\displaystyle [S]_{w}>0}$ ${\displaystyle f''([S])}$ ${\displaystyle [S]=[S]_{w}}$ ${\displaystyle f'''([S])}$ ${\displaystyle f''([S])}$ ${\displaystyle [S]_{w}}$ For any are power functions strictly increasing. So for any , for which is: ${\displaystyle 0<b,c\in \mathbb {R} }$ ${\displaystyle b\rightarrow b^{c}}$ ${\displaystyle \epsilon }$ ${\displaystyle [S]_{w}>\epsilon >0}$ ${\displaystyle ([S]_{w}-\epsilon )^{n{_{H}}}<{[S]_{w}}^{n{_{H}}}\quad \mid \cdot (-(n_{H}+1))<0\quad }$(because of ) ${\displaystyle n_{H}>0>-1}$ ${\displaystyle -([S]_{w}-\epsilon )^{n{_{H}}}(n_{H}+1)>-{[S]_{w}}^{n{_{H}}}(n_{H}+1)\quad \mid +K_{D}(n_{H}-1)}$ ${\displaystyle b([S]_{w}-\epsilon )>b([S]_{w})=0\quad \mid \cdot a([S]_{w}-\epsilon )>0\quad \mid :c([S]_{w}-\epsilon )>0}$ ${\displaystyle f''([S]_{w}-\epsilon )>0}$. For a suitable - environment of is therefore for all (v) ${\displaystyle \epsilon }$ ${\displaystyle [S]_{w}}$ ${\displaystyle f''([S])>0}$ ${\displaystyle [S]\in U_{\epsilon }([S]_{w}),\quad [S]<[S]_{w}.\quad }$ With show starting from ${\displaystyle [S]_{w}+\epsilon >0}$ ${\displaystyle ([S]_{w}+\epsilon )^{n{_{H}}}>[S_{w}]^{n{_{H}}}}$ the corresponding transformations that is for everyone . ${\displaystyle f''([S])<0}$ ${\displaystyle [S]\in U_{\epsilon }([S]_{w}),\quad S>[S]_{w}\quad }$ The latter together with (v) shows the change in sign of in . ${\displaystyle f''([S])}$ ${\displaystyle [S]=[S]_{w}}$

Semi-logarithmic graphs of a Hill equation for different values ​​of ${\displaystyle n_{H}}$

Individual graphs of the Hill equation. The interpretation of the axes is given in the text. in the drawing corresponds in the text. The abscissa does not indicate molar concentrations, but the (dimensionless) ratio . ${\displaystyle n}$ ${\displaystyle n_{H}}$ ${\displaystyle \textstyle {[S] \over K_{A}}}$

In the adjacent diagram, the ordinate is the proportion of substrate-bound enzyme in the total amount of enzyme present. The abscissa indicates the ratio ; it is divided logarithmically. When using the decadic logarithm, is ${\displaystyle \theta }$ ${\displaystyle \textstyle {[S] \over K_{A}}}$

• because of the point "1" zero point of the abscissa and ${\displaystyle \lg(1)=0}$
• because of and the distance between points “1” and “10” length unit of the abscissa. ${\displaystyle \lg(1)=0}$ ${\displaystyle \lg(10)=1}$

For anything , a point on the abscissa that is distant from the zero point denotes the substrate concentration , the factor being readable on the abscissa. Each graph in the diagram shows a Hill equation of the form (6): ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle x}$ ${\displaystyle [S]=10^{x}\cdot K_{A}}$ ${\displaystyle 10^{x}}$

${\displaystyle \theta ={1 \over 1+({K_{A} \over [S]})^{n_{H}}}}$.

Explanation

Each graph in the diagram shows a function ${\displaystyle \theta ={1 \over 1+(10^{-x})^{n_{H}}}}$, as becomes clear by considering the behavior of this function for (at the zero point "1" of the abscissa) and for . Insertion of ${\displaystyle x=0}$ ${\displaystyle x\rightarrow \pm \infty }$ ${\displaystyle (\quad [S]=10^{x}\cdot K_{A}\Leftrightarrow \quad {[S] \over K_{A}}=10^{x}\Leftrightarrow \quad )\quad {K_{A} \over [S]}=10^{-x}}$ shows that every graph also represents a Hill equation of the form (6): ${\displaystyle \theta ={1 \over 1+(10^{-x})^{n_{H}}}={1 \over 1+({K_{A} \over [S]})^{n_{H}}}}$.

For each given Hill coefficient , the graph of the Hill equations for all values ​​of is the same in the diagram , since it does not depend directly on, but on the ratio . The entirety of the graphs forms a (one-parameter) family of directly comparable curves for any positive ; Parts of a hyperbola or pseudo-hyperbolic curves do not occur. ${\displaystyle n_{H}}$ ${\displaystyle K_{A}}$ ${\displaystyle \textstyle \theta }$ ${\displaystyle \textstyle K_{A}}$ ${\displaystyle \textstyle {K_{A} \over [S]}(=10^{-x})}$ ${\displaystyle \textstyle n_{H}}$

Each graph in the diagram is also a graph of a logistic function and therefore has ${\displaystyle f_{n_{H}}\colon x\rightarrow f(x)=\theta }$

• for the asymptote as well ${\displaystyle x\rightarrow \infty \quad (\Leftrightarrow [S]\rightarrow \infty )\quad }$ ${\displaystyle \theta =1}$
• for the asymptote ; ${\displaystyle x\rightarrow -\infty \quad (\Leftrightarrow [S]\rightarrow 0)\quad }$ ${\displaystyle \theta =0}$
• every graph is point-symmetric with a center of symmetry ; ${\displaystyle \textstyle W(1\mid {\frac {1}{2}})}$
• ${\displaystyle W}$is the turning point of every function ; ${\displaystyle f_{n_{H}}}$
• the slope of in is . In this sense, the slope of the graph increases with it. ${\displaystyle f_{n_{H}}}$ ${\displaystyle W}$ ${\displaystyle \textstyle {n_{H}\cdot ln(10) \over 4}\approx 0,5756\cdot n_{H}}$ ${\displaystyle n_{H}}$

proof

The general logistic function can be written: ${\displaystyle f_{G,c,k}:x\rightarrow f(x)=\theta }$ ${\displaystyle \theta ={G \over 1+e^{c}\cdot e^{-kGx}}}$; with has the form: ${\displaystyle \quad G=1,\quad c=0,\quad k=n_{H}\cdot ln(10),\quad [S]=10^{x}\cdot K_{A}\Leftrightarrow \quad {K_{A} \over [S]}=10^{-x}\quad }$ ${\displaystyle f_{n_{H}}}$ ${\displaystyle \theta ={1 \over 1+e^{0}\cdot e^{-ln(10)\cdot n_{H}\cdot 1\cdot x}}=\quad {1 \over 1+1\cdot 10^{-n_{H}\cdot x}}=\quad {1 \over 1+(10^{-x})^{n_{H}}}\quad ={1 \over 1+({K_{A} \over [S]})^{n_{H}}}\quad }$(6) , q. e. d. The characteristics of the general logistic function continue as follows: ${\displaystyle f_{n_{H}}}$ For is asymptote, q. e. d., ${\displaystyle x\rightarrow \infty \quad (\Leftrightarrow 10^{x}\cdot K_{A}=[S]\rightarrow \infty )}$ ${\displaystyle \theta =G=1}$ for is asymptote, q. e. d .; ${\displaystyle x\rightarrow -\infty \quad (\Leftrightarrow 10^{x}\cdot K_{A}=[S]\rightarrow 0)}$ ${\displaystyle \theta =0}$ every graph is point-symmetric with a center of symmetry ; ${\displaystyle \textstyle W(x_{w}\mid {\frac {G}{2}})=W(x_{w}\mid {\frac {1}{2}})}$ with and is , q. e. d .; ${\displaystyle \textstyle x_{w}={c \over k\cdot G}}$ ${\displaystyle \textstyle c=0}$ ${\displaystyle \textstyle x_{w}=0\quad (\Leftrightarrow 10^{x_{w}}=1)}$ ${\displaystyle W}$is the turning point of , q. e. d .; ${\displaystyle f_{n_{H}}}$ the slope of in is q. e. d. ${\displaystyle f_{n_{H}}}$ ${\displaystyle W}$ ${\displaystyle \textstyle {k\cdot G^{2} \over 4}={k \over 4}={n_{H}\cdot ln(10) \over 4}}$

Furthermore, every logistic function belongs to the sigmoid functions , i. H. each of their graphs is S-shaped.

Linearization method

Linearization method were in the past often for quick graphical determination of the important kinetic parameters and used. Although they are memorable and widespread, they lead to a sometimes considerable falsification of the result due to measurement errors and are more or less unsuitable for error analysis. In the meantime, the determination of the Michaelis-Menten parameters by non-linear regression has gained significantly in importance, which leads to significantly more precise results. Therefore, the linearization methods should only be touched upon here. ${\displaystyle K_{m}}$ ${\displaystyle v_{\text{max}}}$

Lineweaver-Burk diagram

Lineweaver-Burk diagram

In 1934 Hans Lineweaver (1907–2009) and Dean Burk (1904–1988) presented a double-reciprocal representation in which is plotted as a function of . ${\displaystyle {\tfrac {1}{v}}}$ ${\displaystyle {\tfrac {1}{[S]}}}$

A transformation of the Michaelis-Menten equation gives the following equation:

${\displaystyle {1 \over v}={K_{m} \over v_{\text{max}}}{1 \over [S]}+{1 \over v_{\text{max}}}}$

Reshaping

${\displaystyle v=\quad {\frac {v_{\mathrm {max} }[S]}{K_{\mathrm {m} }+[S]}};\quad }$ (Michaelis-Menten) Transition to the reciprocal number ${\displaystyle \quad \mid }$ ${\displaystyle {\frac {1}{v}}=\quad {\frac {K_{\mathrm {m} }+[S]}{v_{\mathrm {max} }[S]}}=\quad {\frac {K_{\mathrm {m} }}{v_{\mathrm {max} }[S]}}+{\frac {[S]}{v_{\mathrm {max} }[S]}};}$ ${\displaystyle {1 \over v}={K_{m} \over v_{\text{max}}}{1 \over [S]}+{1 \over v_{\text{max}}};\quad }$ (Lineweaver-Burk)

The slope of this linear function is ; she cuts ${\displaystyle \textstyle {K_{m} \over v_{\text{max}}}}$

• the -axis at ( ordinate section ) and ${\displaystyle \textstyle {\frac {1}{v}}}$ ${\displaystyle \textstyle {\frac {1}{v}}={1 \over v_{\text{max}}}}$
• the -axis at ( abscissa section ). ${\displaystyle \textstyle {1 \over [S]}}$ ${\displaystyle \textstyle {1 \over [S]}=-{\tfrac {1}{K_{m}}}}$

Calculation of intercepts and slope

By taking as an argument of a function, describes the equation ${\displaystyle \textstyle {1 \over [S]}}$ ${\displaystyle {1 \over v}={K_{m} \over v_{\text{max}}}{1 \over [S]}+{1 \over v_{\text{max}}}}$ a linear function . For these, the slope and ordinate segment can be read off directly from the function equation. ${\displaystyle \textstyle {K_{m} \over v_{\text{max}}}}$ ${\displaystyle \textstyle {1 \over v_{\text{max}}}}$ Be ${\displaystyle Q}$ the origin of coordinates, ${\displaystyle R}$the intersection of the graph of the equation with the -axis such that is the ordinate portion of the function, and ${\displaystyle \textstyle {1 \over [v]}}$ ${\displaystyle QR}$ ${\displaystyle P}$is the intersection of the graph of the equation with the -axis such that is the abscissa portion of the function. The coordinate of sei . ${\displaystyle \textstyle {\frac {1}{[S]}}}$ ${\displaystyle PQ}$ ${\displaystyle \textstyle {\frac {1}{[S]}}}$ ${\displaystyle P}$ ${\displaystyle -p}$ Then the triangle is similar to a slope triangle . So the following applies to the ratio of the lengths of the ordinate and abscissa section: ${\displaystyle QRP}$ ${\displaystyle |QR|:|PQ|=\quad {1 \over v_{\text{max}}}:p=\quad {K_{m} \over v_{\text{max}}};\quad \mid \cdot v_{max}}$ ${\displaystyle {1 \over p}=K_{\mathrm {m} };\quad \mid }$Transition to the reciprocal number ${\displaystyle \quad \mid \cdot (-1)}$ ${\displaystyle -p=-{\frac {1}{K_{\mathrm {m} }}}}$as indicated in the drawing.

Although it is mostly used for data representation, this method of analysis is unreliable. Small errors in result in a large deviation in in the case of small values ; in the case of large values ​​this can be neglected. The authors of the method emphasized the uncertainty of large values ​​and pointed out that they should generally be weighted less. Later users have mostly ignored this. Wherever possible, this should be replaced by computer methods for determining enzyme kinetic parameters. ${\displaystyle v}$ ${\displaystyle [S]}$ ${\displaystyle {\tfrac {1}{v}}}$ ${\displaystyle [S]}$ ${\displaystyle {\tfrac {1}{v}}}$

Eadie Hofstee diagram

The Eadie-Hofstee diagram, also Woolf – Eadie – Augustinsson – Hofstee or Eadie – Augustinsson diagram, occupies a middle position. This is understood as a function of . The corresponding transformation of the Michaelis-Menten equation gives: ${\displaystyle v}$ ${\displaystyle {\tfrac {v}{[S]}}}$

${\displaystyle v=-K_{m}{v \over [S]}+v_{\text{max}}}$

Reshaping

${\displaystyle v=\quad {\frac {v_{\mathrm {max} }[S]}{K_{\mathrm {m} }+[S]}};\quad }$ (Michaelis-Menten) ${\displaystyle v=\quad v_{\mathrm {max} }\cdot {\frac {[S]}{K_{\mathrm {m} }+[S]}};\quad \mid \cdot {\frac {K_{\mathrm {m} }+[S]}{[S]}}}$ ${\displaystyle v\cdot {\frac {K_{\mathrm {m} }+[S]}{[S]}}=v_{\mathrm {max} }}$ Forming the left side: insert: ${\displaystyle \quad v\cdot {\frac {K_{\mathrm {m} }+[S]}{[S]}}=\quad v\cdot ({\frac {K_{\mathrm {m} }}{[S]}}+1)=\quad v\cdot {\frac {K_{\mathrm {m} }}{[S]}}+v;\quad }$ ${\displaystyle v\cdot {\frac {K_{\mathrm {m} }}{[S]}}+v=v_{\mathrm {max} }\quad \mid -{\frac {v\cdot K_{\mathrm {m} }}{[S]}}}$ ${\displaystyle v=-K_{\mathrm {m} }\cdot {\frac {v}{[S]}}+v_{\mathrm {max} };\quad }$ (Eadie Hofstee)

From the diagram, you can read off the ordinate section on the axis , and determine it from the (negative) slope of the regression line . ${\displaystyle v}$ ${\displaystyle v_{\text{max}}}$ ${\displaystyle -K_{m}}$ ${\displaystyle K_{m}}$

The error grows with v / [S]. Since v is included in both coordinates, all deviations from the origin converge.

Scatchard diagram

The Scatchard diagram understands the other way around as a function of . It arises from the Eadie-Hofstee diagram by swapping the axes (or equivalent: by mirroring the diagram as a whole at the 1st bisector of the coordinate system). The corresponding transformation of the equation belonging to the Eadie-Hofstee diagram gives: ${\displaystyle v/[S]}$ ${\displaystyle v}$

${\displaystyle {\frac {v}{[S]}}=-{\frac {1}{K_{m}}}\cdot v+{\frac {v_{\text{max}}}{K_{m}}}}$

Reshaping

${\displaystyle v=-K_{m}{v \over [S]}+}$ ${\displaystyle v_{\text{max}};\quad }$ (Eadie Hofstee) ${\displaystyle \quad \mid -v_{\text{max}}}$ ${\displaystyle v-v_{\text{max}}=}$ ${\displaystyle -K_{m}{v \over [S]};\quad \mid :(-K_{m})\neq 0}$ ${\displaystyle {v-v_{\text{max}} \over -K_{m}}=\quad {v_{\text{max}}-v \over K_{m}}=\quad {v \over [S]};}$ ${\displaystyle {v \over [S]}=-{v \over K_{m}}+{v_{\text{max}} \over K_{m}}=\quad -{1 \over K_{m}}\cdot v+{v_{\text{max}} \over K_{m}}.\quad }$(Scatchard)

From the diagram, the axis, which is now the abscissa , can also be read off as the abscissa section , because an ordinate section of the Eadie-Hofstee diagram merges into an abscissa section of the Scatchard diagram due to the aforementioned reflection. The (negative) slope of the regression line can also be determined by transitioning to the reciprocal number and changing the sign . The ordinate section of the straight line in the Scatchard diagram is the fraction mentioned in the section "Direct linear plot" as a measure of the catalytic efficiency. ${\displaystyle v}$ ${\displaystyle v_{\text{max}}}$ ${\displaystyle \textstyle -{1 \over K_{m}}}$ ${\displaystyle K_{m}}$

The Scatchard diagram is mostly used to represent binding measurements (instead of enzyme kinetic data). Scatchard and Eadie-Hofstee diagrams are considered to be the best tools for diagnosing cooperative phenomena. In the case of negative cooperativity or non-identical, isolated binding sites, a concave course with a linear end branch is created. The slopes here correspond to the affinities ( K _d or ) and the total number of binding sites (active centers) can be read from the intersection with the axis. ${\displaystyle K_{m}}$ ${\displaystyle v}$

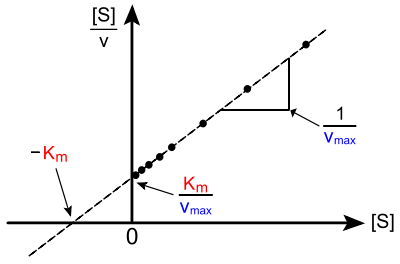
Hanes-Woolf diagram (Hanes (-Wilkinson) diagram)

Hanes-Woolf diagram

The Hanes Woolf diagram is the best possible linear application. It goes back to Charles Samuel Hanes (1903–1990) and Barnet Woolf (1902–1983). A transformation of the Michaelis-Menten equation is used, which represents [S] / v as a function of [S]:

${\displaystyle {[S] \over v}={1 \over v_{\text{max}}}[S]+{K_{m} \over v_{\text{max}}}}$

Reshaping

${\displaystyle v=\quad {\frac {v_{\mathrm {max} }[S]}{K_{\mathrm {m} }+[S]}};}$ ${\displaystyle \quad }$ (Michaelis-Menten) ruptures ${\displaystyle \quad \mid :[S]\neq 0}$ ${\displaystyle \quad \mid }$ ${\displaystyle {\frac {[S]}{v}}=\quad {\frac {K_{\mathrm {m} }+[S]}{v_{\mathrm {max} }}}=\quad {\frac {[S]}{v_{\mathrm {max} }}}+{\frac {K_{\mathrm {m} }}{v_{\mathrm {max} }}};}$ ${\displaystyle {\frac {[S]}{v}}=\quad {\frac {1}{v_{max}}}\cdot [S]+{\frac {K_{\mathrm {m} }}{v_{max}}};\quad }$ (Hanes-Woolf)

The slope of this linear function is ; she cuts ${\displaystyle \textstyle {\frac {1}{v_{\mathrm {max} }}}}$

• the -axis at (ordinate section) and ${\displaystyle \textstyle {\frac {[S]}{v}}}$ ${\displaystyle \textstyle {\frac {[S]}{v}}={\frac {K_{\mathrm {m} }}{v_{\mathrm {max} }}}}$
• the -axis at (abscissa section). ${\displaystyle \textstyle [S]}$ ${\displaystyle \textstyle [S]=-K_{\mathrm {m} }}$

Calculation of intercepts and slope

For the linear function with the equation ${\displaystyle {\frac {[S]}{v}}=\quad {\frac {1}{v_{\mathrm {max} }}}\cdot [S]+{\frac {K_{\mathrm {m} }}{v_{\mathrm {max} }}};\quad }$ the slope and ordinate segment can be read directly from the function equation. ${\displaystyle \textstyle {\frac {1}{v_{\mathrm {max} }}}}$ ${\displaystyle \textstyle {\frac {K_{\mathrm {m} }}{v_{\mathrm {max} }}}}$ Be ${\displaystyle Q}$ the origin of coordinates. ${\displaystyle R}$the intersection of the graph of the equation with the -axis such that is the ordinate portion of the function, and ${\displaystyle \textstyle {[S] \over v}}$ ${\displaystyle QR}$ ${\displaystyle P}$is the intersection of the graph of the equation with the -axis such that is the abscissa portion of the function. The coordinate of sei . ${\displaystyle \textstyle [S]}$ ${\displaystyle PQ}$ ${\displaystyle \textstyle [S]}$ ${\displaystyle P}$ ${\displaystyle -p}$ Then the triangle is similar to a slope triangle . So the following applies to the ratio of the lengths of the ordinate and abscissa section: ${\displaystyle QRP}$ ${\displaystyle |QR|:|PQ|=\quad {\frac {K_{\mathrm {m} }}{v_{\mathrm {max} }}}:p=\quad {\frac {1}{v_{\mathrm {max} }}};\quad \mid \cdot v_{\mathrm {max} }}$ ${\displaystyle {K_{\mathrm {m} } \over p}=\quad 1;\quad \mid \cdot (-p)}$ ${\displaystyle -K_{\mathrm {m} }=\quad -p,\quad }$ as indicated in the drawing.

Errors in [S] / v are a far better approximation of the errors in v. Due to an unadulterated spread of the measuring points along the [S] axis, the result is in principle less falsified by individual outliers. However, since dependent and independent variables are mixed up, data optimization using linear regression does not make sense here either.

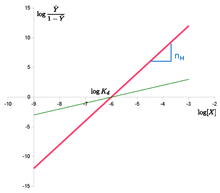
Hill diagram

The Hill diagram is a representation of the Hill equation in which (ordinate value ) is plotted as a function of (abscissa value ). The corresponding transformation of the Hill equation gives: ${\displaystyle \textstyle \log {\theta \over 1-\theta }}$ ${\displaystyle \log {[S]}}$

${\displaystyle \log \left({\dfrac {\theta }{1-\theta }}\right)=n_{H}\log {[S]}-\log {K_{D}};\quad }$(10)

Reshaping

The Hill equation , after replacing the with according to consideration (9), becomes: ${\displaystyle n}$ ${\displaystyle n_{H}}$ ${\displaystyle \theta ={\frac {[S]^{n_{H}}}{K_{D}+[S]^{n_{H}}}};\quad \mid }$ Transition to the reciprocal number ${\displaystyle {\frac {1}{\theta }}={\frac {K_{D}+[S]^{n_{H}}}{[S]^{n_{H}}}}={\frac {K_{D}}{[S]^{n_{H}}}}+1;\quad \mid -1}$ ${\displaystyle {\frac {1}{\theta }}-1={\frac {1-\theta }{\theta }}={\frac {K_{D}}{[S]^{n_{H}}}};\quad \mid }$ Ruptures ${\displaystyle {\frac {\theta }{1-\theta }}={\frac {[S]^{n_{H}}}{K_{D}}};\quad \mid \log }$on a selectable basis ; with the calculation rule for the logarithm of a quotient or the logarithm of a power : ${\displaystyle \log \left({\frac {\theta }{1-\theta }}\right)=\quad \log \left({\frac {[S]^{n_{H}}}{K_{D}}}\right)=\quad \log \left([S]^{n_{H}}\right)-\log K_{D}=\quad n_{H}\cdot \log[S]-\log K_{D};\quad }$(10)

When using (10) has the form: ${\displaystyle K_{A}}$

${\displaystyle \log \left({\dfrac {\theta }{1-\theta }}\right)=n_{H}\log {[S]}-n_{H}\log {K_{A}};\quad }$(10a)

Reshaping

The definition of the half-saturation constant in equation (3 '), after replacing the with according to consideration (9), becomes: ${\displaystyle K_{A}}$ ${\displaystyle n}$ ${\displaystyle n_{H}}$ ${\displaystyle K{_{A}}^{n_{H}}=K_{D}\quad \mid \log }$on the same basis as ${\displaystyle \log {[S]}}$ with the calculation rule for the logarithm of a power : ${\displaystyle n_{H}\log {K_{A}}=\log {K_{D}};}$ this can be used in (10).

Can also take the place of in the following equations . ${\displaystyle n_{H}\log {K_{A}}}$ ${\displaystyle \log {K_{D}}}$

If known, the ordinate values ​​can be determined using : ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle v}$

${\displaystyle \log \left({\dfrac {v}{v_{\mathrm {max} }-v}}\right)=n_{H}\log {[S]}-\log {K_{D}};\quad }$(10b)

Reshaping

Equations (10) and (10b) are equivalent if the argument of the logarithm of the left hand side is the same for both equations. Inserting equation (4) and expanding with gives: ${\displaystyle v_{\mathrm {max} }}$ ${\displaystyle {\theta \over 1-\theta }={{v \over v_{\mathrm {max} }} \over 1-{v \over v_{\mathrm {max} }}}={v \over v_{\mathrm {max} }-v}}$

The saturation function can be introduced into the equation: ${\displaystyle r}$

${\displaystyle \log \left({\dfrac {r}{n_{H}-r}}\right)=n_{H}\log {[S]}-\log {K_{D}};\quad }$(10c)

Reshaping

The definition of the saturation function according to equation (6) becomes after replacing from with according to consideration (9): ${\displaystyle r}$ ${\displaystyle n}$ ${\displaystyle n_{H}}$ ${\displaystyle r=n_{H}\cdot \theta ;\quad }$ (i) Equations (10) and (10c) are equivalent if the argument of the logarithm of the left hand side is the same for both equations. Expanding with and inserting (i) gives: ${\displaystyle n_{H}}$ ${\displaystyle {\frac {\theta }{1-\theta }}={n_{H}\cdot \theta \over n_{H}-n_{H}\cdot \theta }={\frac {r}{n_{H}-r}}}$

Insofar as the Hill equation describes enzyme kinetics correctly, the Hill diagram shows a straight line from which ${\displaystyle g}$

• ${\displaystyle n_{H}}$ than their slope and
• ${\displaystyle \log {K_{A}}}$as abscissa section (= abscissa value of the intersection of with the abscissa) ${\displaystyle g}$

can be read; from this it can also be determined after delogarithmizing and after calculating and then delogarithmizing . ${\displaystyle K_{A}}$ ${\displaystyle \log {K_{D}}=n_{H}\log {K_{A}}}$ ${\displaystyle K_{D}}$

Justification and calculation instructions

A. Those variants of equation (10) that contain the summand have the form ${\displaystyle -\log K_{D}}$ Ordinate value = abscissa value + ordinate segment ${\displaystyle n_{H}\cdot }$ and can therefore be interpreted as a functional rule of a linear function with a slope , the graph of which is the given straight line . ${\displaystyle n_{H}}$ ${\displaystyle g}$ B. To determine the section of the abscissa of such a linear function, its ordinate value must be set to zero: ${\displaystyle \log {[S]}=(\log[S])_{0}}$ ${\displaystyle 0=\quad n_{H}\cdot (\log[S])_{0}-\log {K_{D}}=\quad n_{H}\cdot (\log[S])_{0}-n_{H}\cdot \log {K_{A}};\quad \mid -n_{H}\cdot (\log[S])_{0}\quad \mid :(-n_{H})\neq 0}$ ${\displaystyle (\log[S])_{0}=\log {K_{A}},}$ as indicated in the text. Note: Those variants of equation (10) that contain the summand are straight line equations of the form: ${\displaystyle -n_{H}\log {K_{A}}}$ Ordinate value = abscissa value - abscissa section = (abscissa value - abscissa section) ${\displaystyle n_{H}\cdot }$ ${\displaystyle n_{H}\cdot }$ ${\displaystyle n_{H}\cdot }$ C. If the base of the selected logarithm is so that the abscissa section can be read from the Hill diagram, then the formula for delogarithmizing is . Corresponding to the delogarithmizing of . ${\displaystyle b}$ ${\displaystyle \log {_{b}}{K_{A}}}$ ${\displaystyle K_{A}=b^{\log {_{b}}{K_{A}}}}$ ${\displaystyle \log {_{b}}{K_{D}}}$ From a mathematical point of view, any basis could be used for the calculation described here, but are mostly common the base 10 of the decadic logarithm , which is usually denoted by, so and ${\displaystyle \lg }$ ${\displaystyle K_{A}=10^{\lg {K_{A}}}}$ the base e of the natural logarithm , which is usually denoted by, so ; ${\displaystyle \ln }$ ${\displaystyle K_{A}=e^{\ln {K_{A}}}}$ corresponding to delogarithmizing or . ${\displaystyle \lg {K_{D}}}$ ${\displaystyle \ln {K_{D}}}$ In the Anglo-Saxon language area, not only the general but also the natural logarithm is sometimes referred to (which can lead to confusion). ${\displaystyle \log }$

(Idealized) Hill diagrams; the Hill coefficient is marked with . - Explanation of the axes and their labeling in the text. ${\displaystyle n_{H}}$ ${\displaystyle n}$

In the Hill diagrams opposite, the abscissa variable is denoted with , the abscissa segment with , the ordinate variable with . (The unit of length has been selected differently for both axes , so that the gradient of the red straight line is not . The intersection of a straight line with the ordinate drawn, which does not pass through the zero point of the abscissa, is not the ordinate segment of the respective straight line.) ${\displaystyle \textstyle \log {[S]}}$ ${\displaystyle \textstyle \log {[X]}}$ ${\displaystyle \textstyle \log {K_{A}}}$ ${\displaystyle \textstyle \log {K_{d}}}$ ${\displaystyle \textstyle {\log {\theta \over 1-\theta }}}$ ${\displaystyle \textstyle {\log {Y \over 1-Y}}}$ ${\displaystyle \approx 1}$

For the same abscissa section (and thus the same value of for both straight lines ) ${\displaystyle \textstyle \log {K_{A}}=-6}$ ${\displaystyle K_{A}}$

• the red straight line shows the Hill diagram of a highly cooperative enzyme (section with the ordinate at the slope of the straight line ); ${\displaystyle \textstyle \approx -12\Rightarrow }$ ${\displaystyle \quad \textstyle n_{H}\approx {0-(-12) \over (-6)-(-9)}=4}$
• the green straight line that of an enzyme that is barely cooperative or not cooperating (section with the ordinate at the slope of the straight line ). ${\displaystyle \textstyle \approx -3\Rightarrow }$ ${\displaystyle \quad \textstyle n_{H}\approx {0-(-3) \over (-6)-(-9)}=1}$

If the calculated value pairs do not lie on a straight line, this can be caused not only by random but also by systematic errors, because the Hill equation assumes that the Hill coefficient is the same for all concentrations. GS Adair , who also examined the oxygen binding of hemoglobin, found a deviation from this .

Compilation of linearizations of a hyperbola

${\displaystyle \quad }$

Linearizations of a hyperbola

Inhibitors

Main article: enzyme inhibition

Many drugs and toxins are inhibitors ( inhibitors ) of enzymes. For this reason, the elucidation of the mechanism of action has always been of particular importance. The nomenclature of the inhibitor types was put on a systematic basis by William Wallace Cleland (* 1930) in 1963; unfortunately, terms are still used differently in many textbooks.

However, it should be noted here that classic analyzes are limited to reversibly binding substances. Irreversible binding of a substance to an enzyme leads to inactivation, not to inhibition.

Derived from the Michaelis-Menten equation , the general inhibition equation is as follows: ${\displaystyle v=V_{\text{max}}\cdot [\mathrm {S} ]/(K_{m}+[{\textrm {S}}])}$

${\displaystyle v={\frac {V_{\text{max}}\cdot [\mathrm {S} ]}{K_{m}(1+{\frac {[\mathrm {I} ]}{K_{i}}})+[\mathrm {S} ](1+{\frac {[\mathrm {I} ]}{K_{ii}}})}}}$

Then the ratio of the value (dissociation constant of the complex EI) and the value (dissociation constant of the complex EIS) can be used to derive the type of inhibition: ${\displaystyle Ki}$ ${\displaystyle K{ii}}$

Competitive

Enzyme inhibition

Inhibitor and substrate are mutually exclusive from binding to the enzyme. However, this does not necessarily mean that the inhibitor binds to the same binding site as the substrate. Even if the binding of substrate or inhibitor leads to a conformational change in the enzyme, which blocks the binding site for the other, the inhibition is competitive. However, if the substrate and the inhibitor have the same binding site, then the type of inhibitor is necessarily competitive.

In the case of competitive inhibition, the inhibitor can be displaced from the enzyme by the substrate , so it does not change. However, a higher speed is required for each desired speed , so the apparent speed increases with increasing speed . In the Lineweaver-Burk diagram, this leads to different or to a family of straight lines that have a common intersection on the y-axis at ( ). ${\displaystyle V_{\text{max}}}$ ${\displaystyle [\mathrm {S} ]}$ ${\displaystyle K_{m}}$ ${\displaystyle [\mathrm {I} ]}$ ${\displaystyle [\mathrm {I} ]}$ ${\displaystyle K_{I}}$ ${\displaystyle 1/V_{\text{max}}}$

Incompetitive

The inhibitor does not bind to the free enzyme, but to the ES complex. Higher concentrations of the substrate can therefore not displace the inhibitor from the enzyme, but lead to increased binding. Conversely, binding of the inhibitor reduces the concentration of ES, according to Le Chatelier's principle, additional ES must be formed from E and S: The apparent one decreases, the affinity of the enzyme for the substrate increases with increasing . At the same time, of course, decreases. In the Lineweaver-Burk diagram we find a family of parallel straight lines. ${\displaystyle K_{m}}$ ${\displaystyle [\mathrm {I} ]}$ ${\displaystyle V_{\text{max}}}$

Non-competitive

The inhibitor can bind to both E and ES. In the simplest case , i. This means that the substrate binding does not change the affinity of the enzyme for the inhibitor, for example by changing the conformation. Then of course it also follows that the binding of the inhibitor does not change the affinity of the enzyme for the substrate and . Because of the relationship between and , the binding of inhibitor does not change either . ${\displaystyle K_{i}=K_{ii}}$ ${\displaystyle K_{s}=K_{ss}}$ ${\displaystyle K_{s}}$ ${\displaystyle K_{m}}$ ${\displaystyle K_{m}}$

It can now be shown (by substitution and elimination from the definitions of and ) that . If so , then follows and the apparent increases with it . If on the other hand , then it follows and the apparent decreases with increasing . ${\displaystyle K_{i},K_{ii},K_{s}}$ ${\displaystyle K_{ss}}$ ${\displaystyle K_{i}/K_{ii}=K_{s}/K_{ss}}$ ${\displaystyle K_{i}<K_{ii}}$ ${\displaystyle K_{s}<K_{ss}}$ ${\displaystyle K_{m}}$ ${\displaystyle [\mathrm {I} ]}$ ${\displaystyle K_{i}>K_{ii}}$ ${\displaystyle K_{s}>K_{ss}}$ ${\displaystyle K_{m}}$ ${\displaystyle [\mathrm {I} ]}$

In the Lineweaver-Burk diagram, the non-competitive inhibition leads to a family of straight lines with a common point of intersection to the left of the y-axis, the point of intersection lies on the x-axis if , it lies above the x-axis if and below the x- Axis if . ${\displaystyle K_{i}=K_{ii}}$ ${\displaystyle K_{i}<K_{ii}}$ ${\displaystyle K_{i}>K_{ii}}$

Mixed competitive inhibition

The mechanism of this type of inhibition (which is of little importance in practice) is similar to the non-competitive inhibition, but the EIS complex still has catalytic activity. The Lineweaver-Burk diagram also looks like the non-competitive inhibition (with all 3 possibilities). In the so-called secondary diagram (slope or y-intersection point in the Lineweaver-Burk diagram as a function of ) one sees straight lines in the case of the non-competitive inhibition, but curves in the case of the mixed-competitive inhibition. ${\displaystyle [\mathrm {I} ]}$

See also

• Allostery
• Crabtree effect
• Energy charge
• exergon
• Steady state
• Multi-substrate reaction
• Multi-enzyme complexes
• Pasteur effect
• Substrate cycle
• Change number

literature

• H. Bisswanger: Enzyme kinetics - theory and methods . 3. Edition. Wiley-VCH, Weinheim 2000, ISBN 978-3-527-30096-9 .
• E. Buxbaum: Fundamentals of protein structure and function . Springer, New York 2007, ISBN 978-0-387-26352-6 .
• GE Briggs, JB Haldane: A Note on the Kinetics of Enzyme Action . In: Biochemical Journal . Volume 19, No. 2, 1925, pp. 338-229; PMID 16743508 .
• WW Cleland: The kinetics of enzyme-catalyzed reactions with two or more substrates or products . In: Biochimica et Biophysica Acta . Volume 67, 1963, pp. 104-137, 173-187, 188-196.
• R. Eisenthal, A. Cornish-Bowden: The direct linear plot. A new graphical procedure for estimating enzyme kinetic parameters . In: Biochemical Journal . Volume 139, No. 3, 1974, pp. 715-720; PMID 4854723 .
• JBS Haldane: Graphical methods in enzyme chemistry . In: Nature . Volume 179, 1957, p. 832.
• V. Henri: Theory generale de l'action de quelques diastases . In: Comptes rendues l'Academie des sciences . Volume 135, 1902, pp. 916-919.
• AV Hill: The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves . In: The Journal of Physiology Volume 40, Supplement, 1910, pp. Iv-vii.
• L. Michaelis, ML Menten: The kinetics of the invertin effect . In: Biochemical Journal . Volume 49, 1913, pp. 333-369.
• IH Sails: Enzyme Kinetics . Wiley, New York 1975 (reprinted 1993).
• SPL Sørensen: Enzyme studies II. On the measurement and importance of the hydrogen ion concentration in enzymatic processes . In: Biochemical Journal . Volume 21, 1909, pp. 131-304.

Web links

Wikibooks: Chemistry formula collection / Specific kinetics  - learning and teaching materials

• Peter Birch: An Introduction to Enzyme Kinetics . ( Memento of April 28, 2009 in the Internet Archive ) Department of Biological Sciences, University of Paisley .
• Private website on enzyme kinetics

Individual evidence

1. ↑ The presentation is based on the free formulation of the source named here .
2. ^ AV Hill, "The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves", J Physiol 1910, 40, pp. Iv-vii
3. ↑ cf. z. B. Jachen Denoth: “Theoretical considerations on maximum performance in endurance sports with an energy consumption limited by the maximum oxygen uptake” in: Schweizer Zeitschrift für Sportmedizin und Sporttraumatologie 2008, 65 (2), pp. 77–81
4. ↑ z. B. for the description of a Michaelis-Menten equation in: Hartmut Bossel: "Modellbildung und Simulation", Springer-Verlag, March 13, 2013, p. 271
5. ↑ Hans Bisswanger: “Enzymes: Structure, Kinetics and Applications”, John Wiley & Sons, June 29, 2015, Box 11.2
6. ↑ Berg / Stryer / Tymoczko: Biochemie, p. 214, Springer-Verlag, February 27, 2015.
7. ↑ Scheme drawing for the three options listed in https://images.slideplayer.org/1/649096/slides/slide_39.jpg
8. ↑ The diagram is taken from the English language Wikipedia (page: Hill equation (biochemistry)), the comment is formulated independently.
9. ^ H. Lineweaver, D. Burk: The Determination of Enzyme Dissociation Constants . In: Journal of the American Chemical Society , 56, 1934, pp. 658-666. doi: 10.1021 / ja01318a036 .
10. ↑ Hanes, CS. (1932). Studies on plant amylases: The effect of starch concentration upon the velocity of hydrolysis by the amylase of germinated barley . In: Biochemical Journal 26: 1406-1421; PMID 16744959 ; PMC 1261052 (free full text).
11. ↑ The diagram is taken from the English language Wikipedia (page: Hill equation (biochemistry)), the comment is formulated independently.
12. ^ 'The hemoglobin system. IV. The oxygen dissociation curve of hemoglobin' in: J Biol Chem 63, 1925, pp. 529-545