Moment of inertia
| Physical size | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Surname | Moment of inertia | |||||||||
| Formula symbol | ||||||||||
|
||||||||||
| See also: inertia tensor , moment of inertia | ||||||||||
The moment of inertia , also mass moment of inertia or inertial moment , indicates the inertia of a rigid body in relation to a change in its angular velocity when rotating around a given axis ( torque divided by angular acceleration ). It thus plays the same role as mass in the relationship between force and acceleration ; therefore the term rotating mass is also used in the older literature . It appears as a physical quantity for the first time in 1749 in the work Scientia Navalis by Leonhard Euler .
The moment of inertia depends on the mass distribution in relation to the axis of rotation. The further away a mass element is from the axis of rotation, the more it contributes to the moment of inertia; the distance is a square. If the density of the body increases towards the axis of rotation, its moment of inertia is smaller than if its mass were homogeneously distributed in the same volume. In the case of rapidly rotating planets , the flattening can therefore be used to infer the density profile.
If the axis of rotation is not fixed, a single number is not sufficient to describe the inertia behavior. The moment of inertia for any axis through the center of gravity can be calculated from the inertia tensor .
Illustrative examples
Balancing aid
When Seiltanz be as Balancierhilfe preferred long rods. Compared to a compact body of the same weight, such as a sandbag, such a rod has a very large moment of inertia. Tilting to the side is not prevented by this, but slowed down so that the artist has enough time for a compensatory movement.
You can easily try out the effect yourself: a 30 cm ruler (shorter is more difficult) can be balanced upright on the palm of your hand. However, placed sideways on one of its long edges, it falls over completely before you can react. In both cases, the axis of rotation is the edge lying on top, while the center square of the distance from this axis differs greatly at over 900 cm 2 or around 16 cm 2 .
It is easy to see that the distance is included in the square of the moment of inertia: A given angular acceleration means a tangential acceleration that is twice as large for a mass element at twice the distance and thus twice as large a force of inertia . The torque, double the force × double the lever arm, is four times as large.
Swivel chair and pirouette
Another simple experiment can be used to illustrate a change in the moment of inertia. You sit in the middle of a swiveling office chair and can be made to rotate with your arms and legs stretched out. If you then pull your arms and legs towards your body, the moment of inertia decreases. This leads to the fact that the rotary motion becomes faster because the angular momentum is retained (see conservation of angular momentum ). Reaching out again slows down the movement. To increase the effect, you can put heavy objects in each hand, such as dumbbells. The greater their mass, the more pronounced the effect.
A similar example is the pirouette effect known from figure skating . The speed of rotation can be controlled solely from the displacement of the body mass relative to the axis of rotation. If the figure skater draws his arms or straightens up from a crouching position, he turns faster - there is no need to take another swing.
Formula symbol and unit
The most common symbols for the moment of inertia are and , going back to the Latin word iners , which means inactive and lazy. Since both symbols are also used in electrical engineering, a (large theta ) is still in use. This article is used throughout .
The SI unit of the moment of inertia is kg · m 2 .
Comparison with the mass in linear motion
The moment of inertia in a rotating movement is comparable to the mass of a linear (straight) movement (for details see Rotation (physics) #Comparison with translational movement ). Compare the following equations:
- Rotational movement : torque = moment of inertia times angular acceleration ,
- Translational movement : force = mass times acceleration ( Newton's second law ).
general definition
If the mass distribution of a body is known, the mass moment of inertia can be calculated from the following volume integral:
- .
The part of (see adjacent figure) that is perpendicular to the axis of rotation ( angular velocity ) is here .
Motivation of the definition
Rigid body consisting of mass points

The total kinetic energy of a rigid body , which consists of mass points , results from the sum of the kinetic energies of the individual mass points:
- .
Here is the speed of the ith mass point. Now the whole body should rotate around the axis . Each individual mass point therefore describes a circular path. The orbital velocity of a particle that rotates on a circular path with a radius at the angular velocity can be calculated as. Hence it follows:
- .
Analogous to the definition of kinetic energy
of a linearly moving rigid body of N mass points with the total mass , the moment of inertia of a rotating rigid body of N mass points is defined as
- .
So it applies
- .
With this definition one can identify the following sizes of rotating mass points with the sizes of linearly moved mass points:
- The mass of a rotating body corresponds to the moment of inertia .
- The speed of a rotating body corresponds to the angular speed .
If you choose the z-axis of the coordinate system in the direction of the axis of rotation, the following practical equation can be derived:
- .
Where and are the x and y coordinates of the i-th mass point in the coordinate system chosen in this way. The index "z" is important because the moment of inertia of a body is always related to an axis of rotation (here the z-axis). The equation also shows that the moment of inertia does not depend on the z-coordinates of the individual mass points. The moment of inertia is independent of the coordinates of the mass points in the direction of the axis of rotation.
Rigid body described by mass distribution
The formula for the moment of inertia of a general mass distribution is obtained by imagining the mass distribution made up of many small mass elements . The rotational energy is then through
- .
given. The transition to the integral with the volume of the body composed of the infinitesimal mass elements results
- .
This results in the general definition of the moment of inertia given above with a location-dependent (i.e. generally inhomogeneous) mass density .
Relationship between moment of inertia and angular momentum
The total angular momentum of the rigid body shows i. A. not in the same direction as the angular velocity . The axis-parallel component, however, is given by. This can be seen as follows. The position vector of an individual mass element is divided into a part that is parallel and one that is perpendicular to it. The parallel portion of the position vector does not contribute to the axis-parallel component of the angular momentum of this mass element , it remains:
- .
The axis-parallel component of the total angular momentum then results in
- .
It also follows immediately .
Formulas for important special cases
Homogeneous mass distribution
With a homogeneous mass distribution, the density is locally constant. The density can be pulled in front of the integral and the formula for the moment of inertia is simplified to
- .
An example calculation is given below.
Moment of inertia of rotationally symmetrical bodies
The moment of inertia of rotationally symmetrical bodies rotating around their axis of symmetry (z-axis) can easily be calculated with the help of cylindrical coordinates. To do this, either the height as a function of the radius ( ) or the radius as a function of the z coordinate ( ) must be known. The volume element in cylinder coordinates results in . By integrating over and or over and you get:
- or .
Moment of inertia with respect to mutually parallel axes
If the moment of inertia for an axis through the center of gravity of a body is known, the moment of inertia for any parallel shifted axis of rotation can be calculated with the help of Steiner's theorem . The formula is:
- .
It specifies the distance between the axis through the center of gravity and the axis of rotation that is shifted parallel.
Steiner's theorem can be generalized for any two parallel axes of rotation. To do this, the sentence must be applied twice in a row: First, move the axis of rotation so that it goes through the center of gravity of the body, then to the desired destination.
- .
Theorem about vertical axes
The theorem about vertical axes deals with the special case of flat bodies with a uniform thickness, which can be neglected in comparison with other dimensions of the body. Then the sum of the moments of inertia around any two mutually perpendicular axes of rotation in the plane of the body is equal to the moment of inertia around the axis of rotation, which runs through its point of intersection and perpendicular to the plane of the body. For a body in the xy plane at in the picture that is:
- .
Because then it is calculated
- .
Generalization through inertia tensor
The inertia tensor with components of a body is a generalization of the moment of inertia. In a Cartesian coordinate system, the inertia tensor can be represented as a matrix which is composed of the moments of inertia with respect to the three coordinate axes and the moments of deviation . The three moments of inertia form the main diagonal of the matrix, the moments of deviation are the secondary diagonal elements . With the help of the inertia tensor z. B. calculate the moment of inertia with respect to any axis passing through the center of gravity. If a rigid body rotates around such an axis with angular velocity , the moment of inertia results to
or in matrix notation
- .
Rotation of the coordinate system
An axis in any spatial direction is described by the unit vector . You can z. B. obtained by rotating the unit vector in the z-direction using a rotation matrix R :
With
you get
- .
With the help of this rotation matrix , the inertia tensor can now be transformed into a coordinate system in which the z-axis points in the direction of the rotation axis:
- .
The moment of inertia for the new z-axis is now simply the 3rd diagonal element of the tensor in the new representation. After performing the matrix multiplication and trigonometric transformations, the result is
- .
Example calculation: rotationally symmetrical body
As an example, we consider the inertia tensor of a rotationally symmetrical body. If one of the coordinate axes (here the z-axis) coincides with the symmetry axis, then this tensor is diagonal. The moments of inertia for rotation around the x-axis and the y-axis are equal ( ). The moment of inertia can be different for the z-axis ( ). The inertia tensor has the following form:
- .
If one transforms this tensor as described above into a coordinate system that is rotated by the angle around the y-axis, one obtains:
- .
This results in:
- The moments of inertia for the x and z axes depend on.
- For the inertia tensor is no longer diagonal, there are moments of deviation .
- The moment of inertia for the new z-axis is .
- For hangs due not the moment of inertia on the direction of the axis of rotation.
Special moments of inertia
Main moment of inertia
If you look at a body of any shape that rotates around an axis through its center of mass , its moment of inertia varies depending on the position of this axis of rotation. There is - in general - an axis with respect to which the body's moment of inertia is maximally applied and one for which it is minimally applied. These two axes are always perpendicular to each other and together with a third axis, again perpendicular to the other two, form the main axes of inertia or, for short, the main axes of the body.
In a coordinate system spanned by the main axes of inertia (called the main system of inertia or main axis system), the inertia tensor is diagonal. The moments of inertia belonging to the main axes of inertia are therefore the eigenvalues of the inertia tensor, they are called main moments of inertia .
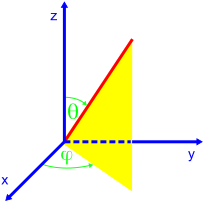
If, as in the picture, a Cartesian coordinate system is aligned in the center of mass parallel to the main system of inertia, the main moments of inertia are calculated as:
if, as usual, the coordinates are numbered according to the scheme x → x 1 , y → x 2 and z → x 3 .
With Binet's moment of inertia (after Jacques Philippe Marie Binet )
the main moments of inertia can also be represented as:
This results in:
The sum of two main moments of inertia is always greater than the third; they satisfy the triangle inequalities .
If the mass distribution is homogeneous, the main axes of inertia coincide with any existing axes of symmetry of the body.
If two main moments of inertia are equal, the rigid body is called a symmetrical top . All axes of rotation in the equatorial plane , which is spanned by the associated main axes of inertia, are also main axes of inertia with the same moment of inertia. This is immediately clear with cylindrically symmetrical bodies, but applies z. B. also for a rod with a square or hexagonal base.
In the event that all three main moments of inertia are identical, as was shown above, each axis of rotation through the center of mass is a main axis of inertia with the same moment of inertia. This applies to all regular bodies such as spheres , equilateral tetrahedra , cube , etc., see spherical top .
Two main axes span a main plane .
Moment of inertia to the clamped axis
If a rigid body rotates around a firmly clamped axis with angular velocity (the direction of the vector is the direction of the axis of rotation), the angular momentum can be calculated from the general formula . In contrast to the formula given above, it is not the moment of inertia but the inertia tensor . In general, the angular momentum does not have the direction of the axis of rotation and is not constant over time, so that the bearings have to constantly apply torque ( dynamic imbalance ). Only for rotation about one of the main axes of inertia is .
For the angular momentum component applies along the axis of rotation , this is the angular velocity and the moment of inertia with respect to the axis of rotation . The kinetic energy of rotation, also referred to as rotational energy for short , can through
be expressed. These formulas show the analogy to the corresponding formulas for momentum and kinetic energy of translational motion.
Examples
Moments of inertia of celestial bodies
Almost all larger bodies in space ( stars , planets ) are approximately spherical and rotate more or less quickly. The moment of inertia around the axis of rotation is always the greatest of the respective celestial body .
The difference between this “polar” and the equatorial moment of inertia is related to the flattening of the body, i.e. its deformation of the pure spherical shape by the centrifugal force of the rotation. In the case of the earth , the difference between these two main moments of inertia is 0.3 percent, which corresponds roughly to the earth's flattening of 1: 298.24. With the rapidly rotating Jupiter , the difference and the flattening is around 20 times greater.
Principal moments of inertia of simple geometric bodies
Unless expressly stated otherwise, the center of gravity of the geometrical bodies lies on the axis of rotation to which the moment of inertia relates. is the mass of the rotating body. The moment of inertia for rotations about other axes can then be calculated using Steiner's theorem . The list of inertia tensors can be used for rotations about any axis .
| Illustration | description | Moment of inertia |
|---|---|---|

|
A point mass spaced around an axis of rotation. | |
b)
|
A cylinder jacket that rotates around its axis of symmetry for one wall thickness . | |
c)
|
A full cylinder that rotates around its axis of symmetry. | |
d)
|
A hollow cylinder that rotates around its axis of symmetry. Includes the aforementioned borderline cases of cylinder jacket and solid cylinder.
|
|

|
A solid cylinder that rotates around a transverse axis (twofold symmetry axis). | |
|
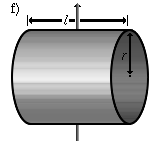
A cylinder jacket that rotates around a transverse axis (twofold symmetry axis). | |

|
A thin rod that rotates around a transverse axis (twofold symmetry axis). This formula is an approximation for a cylinder with . | |

|
Thin rod rotating about a transverse axis through one end. This formula is the application of Steiner's rule to case g). | |
|
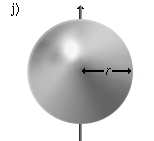
A massive sphere that rotates around an axis through the center. | |
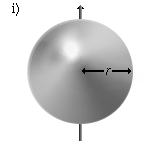
|
A spherical shell that rotates around an axis through the center point, for one wall thickness . | |

|
A hollow sphere that rotates around an axis through the center point for substantial wall thickness | |

|
A cuboid rotating around an axis through the center point that is parallel to its edges c . | |

|
A massive cone that rotates around its axis. | |

|
A cone shell that rotates around its axis. The equality with the moment of inertia of a solid cylinder can be imagined in such a way that you can "flatten" every cone surface to form a circular disk without changing its moment of inertia. | |

|
A massive truncated cone that rotates around its axis. | |

|
A four-sided, regular, massive pyramid that rotates around its axis of symmetry. | |
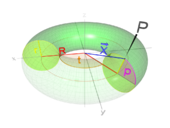
|
Full torus with a radius (red) and half the thickness (yellow) that rotates around the axis of symmetry. (The radius is meant to be the outer radius of the torus ) |
Example calculation: moment of inertia of the homogeneous solid sphere
- Basic knowledge of integral calculus and coordinate transformation is helpful in understanding this section .
In order to calculate the moment of inertia of a massive homogeneous sphere with respect to an axis of rotation through the center of the sphere, the integral given in the "Calculation" section is used. For the sake of simplicity, the center of the sphere should lie at the origin of a Cartesian coordinate system and the axis of rotation should run along the axis. To the integral
it is advisable to use spherical coordinates instead of Cartesian . During the transition, the Cartesian coordinates x, y, z and the volume element d V must be expressed by the spherical coordinates . This is done using the substitution rules
and the functional determinants
- .
Substituting in the expression for the moment of inertia yields
- .
This shows the advantage of spherical coordinates: the integral limits do not depend on one another. The two integrations over r and can therefore be carried out elementarily. The remaining integral in
can through partial integration with
be solved:
- .
For the moment of inertia we finally get:
- .
Measurement
A rotary table is used to measure a body's moment of inertia. This consists of a circular disk, which can be rotated around its axis of symmetry, and a helical spring ( spiral spring ). They effected at a rotation of the disc a rear driving torque which is directly proportional to the deflection angle is . The constant of proportionality is called the directional moment or directional moment . Their value depends on the strength of the spring. The disk now has harmonic oscillations with the period of oscillation
- ,
where is the moment of inertia of the disc. If you now also place a body with a known moment of inertia on the disk, the period of oscillation changes
- .
From the difference between the squares of the respective period of oscillation
the directional moment of the turntable can be determined and the moment of inertia of the turntable can be obtained from the above formula . If you now place any body on the turntable, you can determine its moment of inertia with respect to the axis of rotation from the measured period of oscillation
to calculate.
Moment (integration)
In the natural sciences and technology, moments are parameters of a distribution that describe the position and form of this distribution. They are calculated by integration over the distribution weighted with a power of the distance. In this sense, the mass moment of inertia is related to the area moment of inertia .
Web links
- Moments of inertia of geometric bodies at Matheplanet - Instructions for calculating various moments of inertia with examples.
- Online calculator for moments of inertia
Individual evidence
- ↑ The moment of inertia is explicitly defined by Euler for the first time in Volume 1 (§165, p. 70) in order to obtain a simple expression for the moment effect of inert mass elements when rotating around a fixed axis. The idea that matter has a moment effect that is proportional to the product of the mass of the respective body element and to the square of the distance perpendicular to the axis of rotation, however, goes back further. It can be found both in Euler's earlier writings and in those of his predecessors, which dealt with problems of the center of oscillation of composite body elements. Euler published his first comprehensive theory of rigid bodies and their moments of inertia in 1765 in Theoria motus corporum solidorum seu rigidorum . See Paul Stäckel: Elementary Dynamics of Point Systems and Rigid Bodies . In: F. Klein, C. Müller (Ed.): Encyclopedia of Mathematical Sciences, Volume 4 (Mechanics), Issue 4, Leipzig 1908 . S. 542-547 . Encyclopedia of Mathematical Sciences
- ↑ Demtröder: Experimentalphysik 1. 2008, p. 145.
- ↑ Douglas C. Giancoli: Physics . Ed .: Oliver Eibl. Pearson Deutschland GmbH, Munich 2006, ISBN 978-3-8273-7157-7 , p. 343 ( limited preview in Google Book Search [accessed January 20, 2018]).
- ↑ R. Gammel: The roundabout . Its theory and its applications. 2. revised Edition volume 2 . Springer, Berlin, Göttingen, Heidelberg 1950, DNB 451641280 , p. 26-29 .
- ↑ Grammel (1950), p. 33.
- ↑ a b Wolfgang Demtröder: Experimental physics 1: Mechanics and heat . Gabler Wissenschaftsverlage, 2008, ISBN 978-3-540-79294-9 , p. 147 ( books.google.com [accessed May 30, 2012]).
- ^ A b c d Murray R. Spiegel, John Liu: Mathematical Handbook of Formulas and Tables . McGraw-Hill Professional, 1999, ISBN 978-0-07-038203-9 , pp. 38 ( books.google.com [accessed May 30, 2012]).
- ↑ M. Alonso, E. Finn: Physics. Addison-Wesley, 1995, ISBN 0-201-56518-8 , p. 324.
- ↑ Wolfgang Demtröder: Experimentalphysik 1: Mechanics and heat . Gabler Wissenschaftsverlage, 2008, ISBN 978-3-540-79294-9 , p. 148 ( books.google.com [accessed May 30, 2012]).
- ↑ a b c Wolfgang Demtröder: Experimental physics 1: Mechanics and heat . Gabler Wissenschaftsverlage, 2008, ISBN 978-3-540-79294-9 , p. 149 ( books.google.com [accessed May 30, 2012]).
- ↑ Gitin M. Maitra, LV Prasad: Handbook of Mechanical Design . Tata McGraw-Hill Education, New Delhi 1995, ISBN 0-07-460238-1 , pp. 2-36 ( books.google.com [accessed May 30, 2012]).
- ↑ Gitin M. Maitra, LV Prasad: Handbook of Mechanical Design . Tata McGraw-Hill Education, New Delhi 1995, ISBN 0-07-460238-1 , pp. 2-35 ( books.google.com [accessed May 30, 2012]).
- ↑ Eric W. Weisstein : Torus . In: MathWorld (English).
literature
- Paul A. Tipler : Physics. 3rd corrected reprint of the 1st edition 1994, Spektrum Akademischer Verlag Heidelberg Berlin, 2000, ISBN 3-86025-122-8 .
- Ernst W. Otten: Repetitorium Experimentalphysik. Springer-Verlag Berlin Heidelberg, 1998, ISBN 3-540-62987-4 .
- Torsten Fließbach : Mechanics. 3rd edition, Spektrum Akademischer Verlag, Heidelberg 1999, ISBN 3-8274-0546-7 .
- Herbert Goldstein , Charles Poole, John Safko: Classical mechanics. International Edition, 3rd edition, Pearson / Addison-Wesley, Upper Saddle River, NJ, 2002, ISBN 0-321-18897-7 .
- Wolfgang Demtröder : Experimentalphysik 1. 5. revised and updated edition, Springer-Verlag Berlin Heidelberg, 2008, ISBN 978-3-540-79294-9 .