Color valence
The color valence of a light beam is a physiological parameter. It describes the effect of the light beam on the color- sensitive sensory cells of the human eye . In contrast to the spectral distribution , i.e. the complete information about the spectral colors present in the light beam , the color valence is limited to the less extensive information, which can be represented by three numerical values, which color perception the light beam triggers in the eye.
The color detected by the color receptors of the eye depends on the spectral composition of the light beam. Light rays with the same spectral composition trigger the same irritation of the receptors in the eye. Since the infinitely many visible wavelengths of light are opposed to only three types of color receptors in the eye, humans cannot distinguish all combinations of spectral colors; there are therefore combinations of spectral colors that are different from one another, but trigger the same color stimulus in the eye and thus the same color perception. All light rays that produce the same color perception in the eye are assigned the same color valence - even if they have different spectrally composition ( metamerism ). Light rays of the same color valence behave in the same way in additive color mixtures, so they have the same valence ("valence").
Color valences can be understood as three-dimensional coordinates or vectors in a color space and calculated accordingly. The colorimetry is from those statements that can be derived from this calculation rules in connection with the equality or inequality judgment of the eye. In particular, the calculation rules for additive color mixing follow from this.
The color valence of a light beam can be determined by:
- immediate measurement; an observer compares the light beam with an additive mixture of reference color valences; the color perception properties of the observer's eye are therefore directly included in the measurement.
- by invoice; the color valence is determined from the spectral distribution of the light beam. Such calculation methods model the color-physiological properties of the eye in a mathematical way.
Explanation
Color valence and spectral distribution
Electromagnetic radiation , if it contains wavelengths from the visible range, triggers a color sensation in the eye. Which color is perceived mainly depends on the proportion of the different visible wavelengths in the mixture, i.e. on the spectral distribution of the light.
However, since the human eye only has three different types of color receptors for differentiating colors, the number of possible different color perceptions is smaller than the number of possible different spectral distributions of light. A color receptor cannot distinguish the wavelength at which it is stimulated in its sensitivity range, it can only distinguish stronger and weaker stimuli. Equally strong stimuli can be generated
- by stronger light with a wavelength to which the receptor is less sensitive, or
- by weaker light with a wavelength to which it is more sensitive.
All light rays with spectral distributions that generate the same overall stimuli in the three types of receptors are perceived as having the same color (under the same observation conditions), even if their spectral distributions are different - they have the same color valence. If all possible spectral distributions are divided into classes which each summarize the spectral distributions perceived as having the same color, then the color valence serves to clearly identify these classes.
The color valences of two light rays can be used to decide whether they will trigger the same or different color perceptions:
- Two light rays of the same color valence are perceived as having the same color under the same observation conditions, even if their spectral distributions differ.
- Two light beams of different color stimuli are perceived, however, under otherwise identical conditions of observation as different colors (if the difference is large enough, the color discrimination threshold of the eye to cross).
Color valence and color perception
The color valence is a property of the light that can be objectively determined by measurement technology (e.g. derived from the spectral distribution ) and acts on the eye as a physical color stimulus. It determines which sensory stimulus is triggered in the sensory cells and nerves of the eye, but does not describe what color this sensory stimulus is perceived as in the consciousness of the observer.
This color perception is a complex physiological process in which numerous non-linearities as well as contrast and after-effects are incorporated, which are difficult to grasp using a formula (see color appearance models ). Light that is perceived as a not-too-saturated “orange” in a dark environment is perceived as “brown” in a very bright environment. In a green environment the color appears as “red-brown”, in a red environment as “yellowish brown”. A light beam with a given color valence can therefore be perceived in different ways if it is seen in surroundings with different brightness and color contrast conditions. On the other hand, two lights with the same color valence are perceived as changed, as in the example mentioned, if the observation conditions change, but both change in the same way and maintain their equality with one another.
The same applies to the retuning of the eye: If the eye is exposed to a scene with a dominant overall coloration (for example in a room with reddish incandescent light), it adapts to the situation so that the overall coloration is perceived as more neutral and changes in the course of this retuning change the perceived colors of the individual objects. The change in mood even has an effect for a while: If one eye is closed and thus protected from the change in mood, then both eyes will perceive the sunlit landscape in different colors after leaving the room until a common change in mood is achieved again.
It is essential for the applicability of the color valence, however, that the retuned eye perceives two identical colors as being changed, but as being changed in the same way and therefore still perceives as being the same as one another. The color mood influences the color perception , but not the equality judgment of the eye. The persistence theorem of the physiologist J. v. Kries (1878) therefore states:
"Differently composed color stimuli that appear the same to the neutrally tuned eye (are metameric) also appear the same to the somehow retuned eye."
The judgment of the eye about the equality or inequality of two colors is thus reproducible regardless of the observation conditions . This enables an unambiguous determination of the color valence: two color stimuli have the same color valence precisely when they are indistinguishable in a color comparison.
The eye itself is hardly capable of a reproducible quantitative determination of its color perception beyond the equality judgment. However, this is sufficient to make the color valence unambiguously and quantitatively measurable: If the eye is offered the color valence to be measured in direct comparison with an additive mixture of known color valences and determines equality, then the color valence to be measured is determined by the known intensities of the mixed comparison Color valences determined quantitatively. Since the mixed color stimuli can be objectively measured physically, the same applies to the determined color valence.
properties
Additive color mixing
The color valence describes a property of a light beam that depends linearly (see → spectral values ) on its spectral distribution. If two light beams are superimposed, the spectrum of the sum beam is equal to the sum of the two superimposed spectra. Due to the linear relationship between color valence and spectrum, the color valence of the sum beam is therefore equal to the sum of the color valences of the two superimposed light beams. An additive color mixture can be described simply by adding the color valences of the mixed light rays. With the help of the color valence it is not possible to clearly predict how a color produced by additive color mixing will be perceived, since the perception is also influenced by the respective observation conditions. It can be predicted with which color valence the mixture will be perceived as having the same color under the same observation conditions, or which color valences have to be mixed additively in order to produce a target color valence.
A light beam of a given color valence was " simulated " by suitable additive mixing of light beams of other color valences - the mixture was therefore chosen so that the mixed light has the same color valence as the original light. The spectral distributions of the original and the reproduced light beam will generally be different despite the same color valence. If light of a further color valence is now superimposed (additively) on both the original and the replicated light beam, experience has shown that the mixing result is the same in both cases. The decisive factor for the mixing result is not the spectral distribution of the light rays involved. Knowledge of the color valences is sufficient to be able to predict the mixing result.
Since the effect of a light beam introduced into an additive color mixture on the mixing result depends only on its color valence and not on its spectral distribution ( third Graßmann's law ), the color valence can be defined via its behavior in additive color mixtures :
“Color valence is the property of radiation ('color stimulus') (incident on the eye) that determines the behavior of this color stimulus in the additive mixture with other color stimuli; it describes the 'value' of the radiation for the additive mixture. "
Vectors
As experience shows, three key figures are always required to describe a color valence ( First Graßmann's Law ). In this sense, colors are “three-dimensional” quantities, and color spaces are three-dimensional mathematical spaces. (This is ultimately related to the existence of three types of color receptors in the eye.) Since color valences also behave arithmetically additively in additive color mixing, they show mathematical properties of three-dimensional vectors, so that the rules of vector calculation can be applied to them.
Basis vectors and vector components
Are any three-dimensional vectors , and chosen with the only limitation that they can not lie in a common plane, then any three-dimensional vectors can as the sum of suitable multiple of this so-called basis vectors are represented,
- ,
and a vector is uniquely determined if its “components” , and with respect to the basis vectors , and are given. The vector can therefore be written in the "component representation":
- .
Vector addition
If two vectors and with the components and are given, then the sum vector is obtained by adding components by component:
- .
Multiplication by a number
A vector can be multiplied by a number , the result is a vector that is twice as long. In the component notation, all components must be multiplied by that number:
Change of base
The basis vectors do not have to be perpendicular to one another and they do not have to be of the same length. They can be selected in the way that is most convenient for the task at hand. If a different set of basis vectors is used, the components of the vector under consideration change . The components related to the first base are converted into the components related to the second base as follows:
In addition to the basis vectors a second set of basis vectors added, and the components of the are coated basis vectors with respect to the unprimed basis vectors known
- ,
so the components of the unprimed basis vectors with respect to the primed basis vectors are known, and it is
- ,
wherein the coefficient matrix formed from the is the inverse of that formed from the coefficient matrix.
A given vector can be expressed in terms of both sets of basis vectors:
Comparison of the first and last lines shows that the vector components relating to the primed basis are related to the components relating to the uncoated basis as follows:
Similarly, the conversion in the opposite direction results in:
Color valences as vectors
In colorimetry, the color valences are treated as vectors ; in particular, the calculation rules just explained for vectors apply. The entirety of all (possible) color valence vectors forms the three-dimensional color space , the tip of each color valence vector marks a color location in the color space.
Color value
The length of a color valence vector is called the color value . Is a color valence as an additive mixture of two color valences and given
so are and the color values with which and occur in the mixture, the color value can therefore (with regard to the given color values and ) also be written in the component representation with the color values . The units of the color values are initially determined by the arbitrarily chosen lengths of the base vectors and (for the selection of a scale, see the sections → Scaling and white point and → Brightness of light and body colors ).
Chromaticity
If the brightnesses of the two additively mixed light beams are changed with the color valences and by the same factor , experience shows that the mixing result only changes with regard to its brightness. A family of colors that differ from each other only in their lightness is called colors of the same hue
In the vector sum display the new sum vector has
the times the length, but the same direction as the original vector . The chromaticity is indicated by the direction of the color valence vector.
Primary valences
The basic color values selected as basic vectors for the vector sum or component representation of any color value are called primary values. If a set of three primary valences is selected, each color valence (since it is three-dimensional) can be represented as a vector sum of the three primary valences:
or in the component representation as a triplet of color values:
- .
Change of primary valences
In principle, the primary valences can be chosen as desired. The conversion of the color values that describe a color valence with regard to the old primary valences into the color values that they describe with regard to the new primary valences is carried out analogously to the calculation rules explained above for the base change in vector calculation. This operation is often used in colorimetry. It allows, for example, the measurement of color valences with respect to a set of primary valences which is easily accessible for the measurement, while the practical application can take place with regard to a set of primary valences that is convenient in other respects.
Abney's law
According to Abney's law (after William de Wiveleslie Abney ), the luminance of a color valence with the color values applies :
- .
I.e. the greater its color values, the greater the brightness of a color valence. Each of the primaries , and transmits proportional to their color value , and the overall luminance of the color stimulus at. The proportionality factors are called luminance coefficients; they are the luminances of the unit amounts of the relevant primary valences.
The additivity described by Abney's law generally only applies to photometric quantities such as luminance. For the perceived brightness, it only applies approximately and only in cases of low color intensity.
Measurement
A typical arrangement for the direct measurement of color valences shows the observer a color field surrounded by a neutral environment, which is divided into two halves. One half contains the color to be reproduced (generated for example by a projector with a color filter , by a color spinning top), the immediately adjacent second half contains an additive mixture of the primary valences used for the experiment (generated for example by projectors with suitable color filters).
The observer regulates the intensities of the primary valences until both halves of the color field appear the same color. The experimental conditions ensure that both color stimuli are viewed under the same observation conditions, i.e. that the equality of the color valences can be inferred from the equality of color perception . After calibration, the set intensities correspond to the color values of the reproduced color valence.
It is of particular interest to simulate the spectral colors. If their color values are known (→ spectral values ), the color values of all other color valences can be determined mathematically if the spectral distribution is known.
Color value proportions and color tables
The three-dimensional nature of color valence vectors makes them difficult to visualize. Since the lightness is often of less interest than the chrominance of a color valence, it is possible to switch from the color values of a color value to the color value components by dividing each of the three color values by the sum of all three color values:
Because one of the three variables can always be calculated from the other two, it does not carry any independent information and can be omitted without loss. The two remaining color value components, for example and , can be plotted in a two-dimensional diagram.
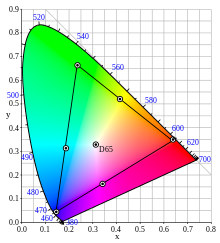
The above formulas can be understood as the projection of the color valence vectors onto the plane in the color space which is described by the condition . This plane lies obliquely in the color space and goes through the tips of the primary valence vectors , and . All vectors with the same direction (i.e. the same color type) penetrate this plane at the same point , which therefore represents the relevant color type. The two-dimensional diagram in this level is therefore a "chromaticity diagram" or, for short, a color table. All color valences are arranged on it according to their color type and without the brightness information. The best known of these color charts is the CIE standard color chart .
From the construction of the color table it follows that the color types of all color valences, which can be represented as an additive mixture of two given color values, lie in the color table on the straight line connecting the given color types. If three color valences are mixed additively, then the color types of all color values that can be mixed from them lie in the color table in a triangle, the corners of which are formed by the color types of the three given color values. The illustration shows such a gamut triangle using the example of the CIE standard color table.
Inner and outer blend
The components of a mathematical vector can have both positive and negative signs. The color values of a color valence can be understood as the intensities of a set of additively mixed primary valences. Since light cannot have a negative intensity, only positive color values seem to be possible at first. However, it proves to be advantageous to also allow negative color values mathematically.
If the three primary valence vectors are assumed to be infinitely extended and the volume spanned between them is considered (an infinitely long "bag" with a triangular cross-section), then all color valences that are a sum of positive multiples of the primary valences and therefore have three positive color values are in Interior of this volume (the intersection of this volume with the color table plane is the gamut triangle mentioned in the last section); the color valences lying outside this volume have at least one negative color value.
Negative color values are not an obstacle when calculating with color valences. Really additively mixable and "showable" are only color valences with exclusively positive color values, provided that the three primary valences are "showable".
Inner mix
An additive inner mixture exists if it only contains positive parts of the mixed primary valences. In this case, the mixed valence lies within the volume that is spanned by the primary valences, i.e. H. within the gamut triangle of the color table.
Outer mix
An additive external mixture exists when the target valence has negative color values. It is therefore outside the volume that can be additively mixed from the given primary valences, i.e. H. outside the gamut triangle of the color table.
If, in a colorimetric measurement that can only work with really "showable" colors, a given color value is to be reproduced by the additive mixture of three primary values given by the measuring apparatus , this is not possible if it has negative color values for at least one of these primary values (cf. . Fig.).
In this case a trick can be used. For example, the color valence should
with a negative color value can be adjusted by additive mixing of , and . By moving
a color equation with exclusively positive color values can be made from this. In terms of instrumentation, this means that a positive proportion of the primary valence is added to the target valence and thus a new target valence is generated which can be reproduced using the primary valences and with positive color values. Although the original target value is no longer displayed, the setting found clearly indicates their color values, correctly taking into account the signs.
In a color chart (see chart.) Means this approach is that a chromaticity represented by the primaries outside of , and is spanned gamut triangle, by admixing a suitable amount of the closest side of the triangle is brought (at point ); then the two primary valences and , which span this side, can be mixed additively in the usual way.
Negative color values of a given color valence can always be avoided by a suitable choice of the primary valences. They are therefore only a property of the representation of a color value by color values with respect to a given set of primary values, but not a property of the color value itself . In a color table this means that for every color point (or for most of them) a triangle of primary valences can be found in which it is contained.
Spectral values
Since a light beam of any spectral distribution can always be understood as an additive mixture of monochromatic light beams (i.e. the individual "spectral colors" contained in the mixture), the color valence of the light beam can be calculated as the sum of the color valences of the spectral colors involved, if the color valences assigned to the individual spectral colors and the proportions of the spectral colors in the mixture are known.
Let be the spectral distribution of the considered light beam. The radiation power is then allotted to a small wavelength interval containing the wavelength . The entire light beam is an additive mixture of "monochromatic" light beams (i.e. light beams that only cover a small range of wavelengths ). The color valence of the light beam is the sum of the color valences of the monochromatic light components :
- .
On the other hand, as always, it can be expressed as a triple of color values with respect to a given set of primary valences :
- .
Energy-like spectrum and color equation
Of particular interest in colorimetry is that spectral distribution which has the same value for all wavelengths:
- .
This spectral distribution is referred to as the "energy spectrum".
For the color valence of a monochromatic light beam from a spectrum of the same energy the color equation applies with regard to the primary valences :
- .
Spectral values
The color values for a monochromatic light beam of the wavelength , which was taken from light with the same energy spectrum, are called spectral values . They are usually denoted by lowercase letters that are overlined. (Note the use of lower case letters, although these are color values and not color value components. The overline is reminiscent of the energy spectrum).
When measuring the spectral values, it is difficult to actually produce a spectrum with the same energy. Instead, any spectrum can be used, the radiant power measured, which is allotted to the respective wavelength interval, and the measured color values divided by the scaling factor in order to convert them into the spectral values for the respective wavelength.
If, instead of an absolute, relative measurement of the radiation power is carried out, the color values that were determined with the aid of the spectral values from the spectral distribution are only determined up to an unknown constant . If only the relationships between the color values are of interest (e.g. in the form of the color value components), then this constant is shortened. On the other hand, if the color values themselves are of interest, the constant can be accessed in various ways, see the section → Brightness of light and body colors .
The color valence of any light beam with the spectrum with respect to given primary valences can be determined if the spectral values with respect to these primary valences are known. The monochromatic partial light beam in the wavelength interval has a radiation power that is a factor greater than the partial light beam of the same wavelength in the spectrum of the same energy, so the relevant color valence vector is a factor longer than the color valence vector :
The sum over all wavelength intervals results in
The comparison of the first and the last line shows that the color values can be calculated from their spectral distribution :
If the wavelength intervals infinitely small, the sums pass into integrals from k urzwelligen to l extend angwelligen end of the visible wavelength range:
The color values result from integration over the spectral distribution, which is weighted with the respective spectral value; this is the linear relationship mentioned at the beginning between the spectral distribution and the associated color valence. In practice, however, the o. G. Sums are used because the spectral values are usually tabulated.
Two light rays with the spectral distributions and have the same color valence if applies
The spectral value functions only have to be determined experimentally once and for all (for given observation conditions). It is even sufficient to determine it only once for a certain set of primary valences, since the spectral value functions for other primary valences can be derived from them by changing the base (see above).
Spectral color train and virtual colors

Are from the spectral values , and formed the Spektralwertanteile
and the coordinates for all visible wavelengths are entered in a color table, the result is the “spectral color path” of this color table (see Fig.). The spectral color train is a curve that is convexly curved everywhere .
Real colors
Since all colors visible to the eye can be understood as additive mixtures of spectral colors and additive mixtures in the color table always lie on the straight connecting line between the two mixed color types , all visible ("real") colors must be within the spectral color range.
All types of color that can be obtained from three primary valences through internal mixing lie within the gamut triangle that is spanned by the associated primary colors in the color table. Since the range of real colors is limited by a curved curve, but every gamut triangle has straight sides, there is no gamut triangle spanned from real (i.e. within the spectral range or on it) primary colors that could cover all real colors.
Virtual colors
Points outside of the spectral color range do not correspond to any visible color types, they nevertheless have their color type coordinates in the diagram and can be mathematically treated in the same way as real colors; they are referred to as "virtual" (sometimes "imaginary") colors.
If virtual color valences are also permitted as primary valences, the color types of which are outside the spectral color range, then they can be selected in such a way that the gamut triangle spanned by them completely encompasses the spectral color range and thus all visible color types. For example, were standard primaries , , selected from this point: You yourself are outside the Spektralfarbenzuges and therefore virtual color stimulus, but all visible color modes can be calculated from their mixing to additively by internal mixing.
Scaling and white point
The color values , and are numbers which indicate the respective associated primary valence vector which multiples , or in a color stimulus vector is included. A color value unit is therefore identical to the length of the relevant primary valence vector. These lengths are initially chosen arbitrarily and can also be different for the different primary valence vectors.
In order to limit this arbitrariness, it would be possible to measure the primary valences in photometric physical units, for example as a multiple of the luminance unit 1 cd / m². However, this means that achromatic color valences have color values of very different sizes (an example follows below ) and is perceived as impractical.
Instead, it was stipulated that a certain selected color value should be described by a set of identical color values and that the units should be chosen in such a way that an additive mixture of one unit of each of the primary values results in the selected color value. The color value components of the color values scaled in this way are
- .
(In this way, only the relative units of the color values and thus the color type are clearly defined. For the absolute scaling of this color value triple, see the section → Brightness of light and body colors .)
In principle, any color type could serve as a reference, but for practical reasons they should be roughly “in the middle” of the possible color types. They are therefore selected from the range of achromatic color types and the coordinates of the color type white and specifically assigned to the color type of the spectrum of the same energy.
The choice of a spectrum with the same energy as the white point must not be understood to mean that this spectrum (which does not exist anywhere in nature) is the “whitest color type” and thus the definition of “white” par excellence. Due to the ability to change the mood mentioned at the beginning, every approximately white light color appears to the eye as white after a short period of familiarization. There is therefore no clear white light. If a series of approximately white but not identical light colors are offered, the eye adjusts itself to the dominant lighting, perceiving it as white and the other lights as having a color cast in comparison . If the eye adjusts to one of the other light colors, the roles are reversed.
Historically, different light sources were used as a white point. The use of the spectrum of the same energy is advantageous from a mathematical point of view. If color valences are to be determined for a real situation in which the eye is attuned to a certain type of light (e.g. daylight , incandescent light, fluorescent light - all of slightly different color types), the color table is new to the color type of this type of light to center. A simple but usually sufficient method for this is the von Kries transformation, which redefines the relative units of the primary valence vectors (and thus simulates “fatigue” of the eye for certain primary valences).
For example, the daylight-like standard illuminant D 65 in the standard color table has the color value components and , so it is somewhat bluer compared to the spectrum of the same energy and would not be seen as white by an eye attuned to the spectrum of the same energy, but as slightly bluish. If the eye adjusts itself to illumination by D 65 , this now moves to the white point a = 1/3, b = 1/3. The color type of the spectrum with the same energy is no longer on the white point in the newly centered color table, but appears somewhat reddish to the eye tuned to D 65 .
Frequently used primary valences
The previous explanations apply generally to any primary valences , and . Some frequently used primary valence triples are presented below.
Instrumental primary valences CIE-RGB
Early measurements of spectral value functions were made by JC Maxwell , A. König and C. Dieterici , and W. Abney . The spectral value functions used as a standard today go back to the experimentally determined data by J. Guild and WD Wright around 1930. Guild (1931, 7 subjects) and Wright (1928–1929, 10 subjects) each determined spectral values using a 2 °, two-part comparison field:
- Guild generated the primary valences to be mixed with a tungsten light bulb ( color temperature 2900 K ), from whose spectrum he isolated relatively broad red, green and blue wavelength ranges by means of filters. A normal NPL lamp with a color temperature of around 4800 K served as the white point for the relative scaling of the spectral values .
- Wright used monochromatic primary valences with the wavelengths 650, 530 and 460 nm . He used an alternative method for scaling, but determined the color value proportions of the NPL lamp standard with respect to its primary valences in order to enable a conversion between the two systems.
A comparison of the two data sets - after conversion to the same primary valences - showed surprisingly good agreement despite the different apparatus and procedures, so that a combined data set could be regarded as representative for the average observer.
The CIE laid down in 1931 spectral value, which represented the average of the records of Guild and Wright after they set up also by the CIE primaries , and had been converted. The hypothetical observer, whose color receptors have the properties described by these spectral value functions, is the “2 ° colorimetric standard observer CIE 1931”.
The CIE-RGB system is based on monochromatic primary valences with the wavelengths
- 700.0 nm ( )
- 546.1 nm ( )
- 435.8 nm ( ).
The wavelength 700.0 nm is at the red end of the spectrum, where the hue changes only slightly with wavelength; 546.1 and 435.8 nm are prominent green and violet lines in the mercury spectrum , which can be easily and clearly generated. The relative scaling of the color values was chosen so that the color stimulus of the spectrum with the same energy (instead of the NPL white) has the same color value components .
In order to generate the white of the energy-equivalent spectrum with a luminance of 1 cd / m², the following luminances of the additively mixed primary valences are required:
The RGB primary valences are therefore by no means contained in a white in the same luminance proportions. As explained above , for practical reasons the units for the color values are chosen so that
- one unit of the color value corresponds to the luminance 0.17697 cd / m²
- one unit of the color value corresponds to the luminance 0.81240 cd / m²
- a unit of the color value corresponds to the luminance 0.01063 cd / m² (or equal multiples thereof).
The following applies to the color values of the white point .
As the spectral diagram shows the CIE RGB primaries, the spectral values are , , and thus the Spektralwertanteile partially negative numbers. This is because the entire gamut triangle lies within the spectral color train (with the exception of the corners that lie on the spectral color train). The spectral colors (with the exception of the three spectral colors used as primary valences) are outside the gamut and can only be produced by external mixing, which results in negative color values.
Standard valences XYZ
The CIE conducted in 1931 at the same time a second set of spectral functions , , one that results from the RGB set by conversion to new stimuli , and results and has very convenient features.
Positive color values
The occurrence of negative spectral values was inconvenient for the manual calculations at that time and should be avoided in the XYZ system. It was necessary that new stimuli , and so to choose that spanned from them gamut triangle enclosing the spectral color curve completely, allowing to generate all spectral color stimuli by internal mixture of the primaries. Since the primary valences must lie outside of the spectral color range, they are necessarily virtual color valences and cannot be represented physically.
The vectors that represent the primary valences , and are in the color space , outside the range of the vectors that represent real color valences. In the color table, the types of colors of the primary valences lie outside the range of real types of color that is limited by the spectral range, and the gamut triangle formed by them completely encloses the range of real types of color. This ensures that the chromaticity coordinates , , and the color values , , any real color stimuli are never negative.
Y as light sensitivity level
It has proven to be beneficial to separate the information about the luminance of the color from the information about the type of color. If the luminance is not required, only the chromaticity information has to be used. However, if the luminance is required, it is available immediately.
For color valences in the CIE-RGB space, Abney's law applies to zero luminance,
this formula describes the level in the color space in which the color valences have zero luminance. This level is called "Alychne" ( the lightless ). If color valences from the Alychnen level are selected as primary valences and , then they have the luminance zero and do not contribute to the luminance of an observed color value. The brightness information is now only carried by the color value of the primary valence . That this role was chosen and not or is just a convention with no deeper reason.
It remains to be specified. The wavelength-dependent light sensitivity of the photometric standard observer for light stimuli is described by the V (λ) curve . Under very general conditions, V (λ) can always be represented as a linear combination of colorimetric spectral value functions. Since the spectral functions , , located in transforming to anyway as linear combinations of , , give, can be for one of them (you choose randomly ) choose the linear combination so that just V (λ) results:
For a given light stimulus of the spectral distribution , the color value is obtained as an integral over the spectral distribution weighted with the spectral value function (see section → Spectral values ):
At the same time, this is nothing more than the formula for determining a photometric quantity from the spectral distribution of the associated radiometric quantity (see, for example, the → definition of the luminous flux ). To choose the factor, see the section → Brightness of light and body colors . The colorimetric standard observer defined by the spectral value functions defined by the CIE is in this way at the same time a photometric standard observer.
Abney's law takes a particularly simple form in the color space: The luminance coefficients are
- ,
and it applies, as assumed:
Other properties
Further properties specified for the complete definition of the XYZ space are: In the color table, the point representing the chromaticity of lies on the straight extension of the long-wave end of the spectral color train. The side of the triangle touches the spectrum color train. The position of the chromaticity point of is chosen so that the triangle encloses the smallest possible area.
If it is also determined (arbitrarily) that the resulting gamut triangle should be displayed as a right-angled isosceles triangle, the result is the color table.
The axis of the color table is the line of intersection of the color table plane with the arylene plane (it is therefore sometimes referred to as the "arylene track"). It lies outside the range of real color types: Really representable color valences must have a luminance that is greater than zero.
standardization
The color measurement standard DIN 5033 adopts the recommendation of the CIE and provides for the use of the XYZ color space for "color description of materials and lights on a metric basis". The standardized primaries , , therefore, are called Normvalenzen. The color values , , hot standard color values. The chromaticity coordinates , , hot chromaticity. The spectral , , hot tristimulus values. The color table is called the standard color table.
XYZ coordinates
The following applies to the standard color value components
- ,
wherein is again redundant. and , as always with color value components, only contain color information but no brightness information. If the color value , which contains brightness but no color information, is added, the frequently used coordinates are obtained. Are , and if so, the color values are calculated , , from using the formulas
Transformation from CIE-RGB to XYZ
The matrix for the transformation from the CIE RGB system to the XYZ standard valence system is:
The second line contains Abney's law with the luminance coefficients already mentioned for the RGB primary valences.
The row sums of the matrix are all equal to one. From this it follows in particular that if they are the same, they are also the same. The new white point is therefore identical to the old white point. The matrix can be modified in such a way that it simultaneously changes the white point when the primary valence changes.
Large field standard valences X 10 Y 10 Z 10
The measurements by Guild and Wright, on which the standard spectral values are based, were made with 2 ° color fields. The choice of this small size was based, on the one hand, on the fact that there are no rods in the area of the retina covered by it , whose possible interference in the visual process would have falsified the spectral values due to their different spectral sensitivity . On the other hand, the yellow spot on the retina , which acts as a color filter, is relatively uniform in this central area. The CIE recommends the use of the standard spectral values of the "2 ° normal observer" ( see above ) for colored areas with extensions between one and four degrees, in practice they are also used for smaller colored areas.
Since most visual processes in everyday life affect larger colored areas, spectral value functions were also measured on larger colored areas later. These data sets define the "colorimetric CIE 10 ° standard observer 1964". Sufficiently high luminance levels had to be used in the measurements to prevent the rods from participating. Since the yellow spot has a diameter of about 5 °, it affects the color perception of the 10 ° observer less than that of the 2 ° observer.
The construction principles of the X 10 Y 10 Z 10 color space correspond to those of the XYZ color space. In particular, the following applies to the color values of the spectrum of the same energy as the white point:
- .
The brightness sensitivity curve V (λ) can not be represented as a linear combination of the 10 ° spectral value curves . It can therefore happen that two color stimuli in the 10 ° standard valence system have the same color valence and yet - weighted with V (λ) - have slightly different luminance levels; since the V (λ) curve relates to a photometric 2 ° observer, this is not a physical contradiction. The spectral value function can be interpreted as a light sensitivity curve V 10 (λ) for colored areas with a diameter of about 10 °.
A conversion between the 2 ° colorimetric standard observer and the 10 ° standard observer is not possible. In any case, there is no linear transformation between the two systems, since color stimuli that look the same color in one system can look different colors in the other and vice versa. The data must each be measured separately or calculated separately from the spectral distribution of the color stimulus.
The CIE recommends the use of the 10 ° standard observer for colored areas over 4 ° in diameter.
Base valences LMS
The Grundvalenzen , , those three primaries, whose associated spectral value are identical with the wavelength-dependent sensitivity curves of the three color receptor types of the retina.
Since the sensitivity curves generally cannot assume negative numerical values, the three spectral value functions of the LMS system must also have exclusively non-negative values. This is only possible if all spectral colors (and thus all other real colors) can only be mixed by an internal mixture of the basic valences. The three basic valences must consequently span a gamut triangle that completely encloses the spectral color range, i.e. they themselves must lie outside the spectral color range . They are therefore (similar to the standard valences) virtual primary valences. Each of them corresponds to the color valence that the associated color receptor species would “see” if it were stimulated on its own. Because of the overlap of the sensitivity ranges, however, it is not possible to stimulate one type of receptor alone, and none of the fundamental valences can actually be generated.
The basic valences can be determined by comparing color adjustment experiments with normal-sighted and with dichromatic color-defective test persons ; in the latter, one of the receptor types is not functional.
- A test person with normal vision can, for example, distinguish between all real color valences that can be produced by variable admixture of the primary valence (red) to a given color valence . In a color table, all these mixed color types lie on the straight connecting line between the color type of and the color type of .
- These distinctions, which are based only on different excitations of the L-receptors, are not possible for a protanope because its L-receptors are not functional. He cannot distinguish between all the colors along the connecting line. If several such color mix-up lines are determined distributed over the color table, which result for several given color valences and each variable admixture of the fixed primary valence , then these straight lines intersect at a point outside the range of real colors; this point corresponds to the position of in the color table.
Accordingly, the color coordinates of and can also be determined experimentally.
The conversion between the standard valence area and the basic valence area is done using the following matrix:
Applying this transformation to the color matching functions , , gives the Grundspektralwertfunktion , , . These have neither negative numerical values nor secondary maxima and can be viewed as spectral sensitivity curves of the three types of color receptors.
Applied to a color valence , the transformation provides a measure of the irritation of the individual receptor types L, M, S by this color valence. The scaling is again selected so that the white point is retained.
Instead of the small field Normvalenzen , , the transformation can also to the large field Normvalenzen , , are applied.
Monitor primary valences RGB
Color monitors generate the colored image content to be displayed by additive mixing of the contributions from brightly colored pixels . Each pixel emits light in one of three colors, which is specified by the phosphor or filter used for this point .
The larger the gamut triangle spanned by the three technically specified primary valences, the larger the color range that can be displayed by the monitor. In order to achieve the largest possible triangle, the primary valences must be selected from the range of red, green and blue color valences (the "corners" of the color table). In the interests of a large gamut, the primary valences should be spectral colors as far as possible so that the corners of the gamut triangle extend to the spectral color range. Corresponding phosphors, however, only have a low luminosity, since they are only allowed to shine on a tiny part of the available spectrum. The choice of the primary valences is therefore a compromise between the gamut size on the one hand and the luminosity and the technical and commercial availability of the phosphors on the other.
A frequently used set of monitor primary valencies are the sRGB primary valencies. Your standard chromaticity coordinates are:
The conversion from the standard valence system to the sRGB primary valence system is done using
where , and are normalized standard color values.
Brightness of light and body colors
In the equations
the factor has not yet been determined. If only the relationships between the color values are of interest (e.g. the color value proportions ), this factor is reduced further. However, if the brightness of the light beam is to be specified, it must be determined explicitly. Since the standard valences are chosen so that the brightness information is only carried by the standard color value , it is sufficient to simply use the equation
consider; the equations for and are then assigned the same resulting numerical value for .
While the color valence of a light beam falling into the eye of the spectral distribution has been explained independently of its origin and previous history, it now makes sense to differentiate according to the origin and the perception of the light observed.
Light colors
If the light beam to be described colorimetrically comes directly from a light source with the spectral distribution , then this spectral distribution arrives unchanged at the eye:
- .
The intensity of the light emitted from a surface is described by a suitable photometric variable , depending on the emission geometry and the issue, for example luminance , luminous intensity or luminous flux . With the corresponding radiometric quantity (for example, radiance , radiant intensity , radiation power ) depends photometric size as follows:
With
- the maximum value of the photometric radiation equivalent during daytime vision
- the relative spectral brightness sensitivity of the eye
- the spectral distribution of the radiometric quantity .
Luminance is usually used as a photometric quantity in a colorimetric context , as it is a direct measure of the brightness of a surface as perceived by the eye:
with the spectral distribution of the measured radiance.
Comparison with the equation for the standard color value in the previous section shows that is identical to the luminance:
- ,
if is set:
- .
In this case, the fact that the tristimulus values , , are given in absolute units (for example in the units of luminance cd / m²), can be emphasized by applying indices, for example , , .
The same procedure can be used if the light intensity is described by other photometric quantities such as luminous intensity or luminous flux; the standard color values then carry the relevant units.
In cases in which absolute standard color values are not important or only relative standard color values are known, but in which standard color values should nevertheless be specified, the standard color value can be set to 100 at will. For example, the standard illuminants are only defined by relative spectral distributions. An indication of the standard color values and standard color value components for standard illuminant A would be:
Body colors
If an illuminated, not self-luminous colored object is viewed, the spectral distribution of the light stimulus falling on the eye is given by:
- ,
With
- the spectral reflectivity of the object
- the spectral distribution of the illuminating light source.
The spectral distribution that catches the eye is thus - unlike self-illuminating light sources - not only determined by the optical properties of the light source, but also by those of the illuminated body, especially by the wavelength-dependent reflectivity of its surface.
If the luminance of the reflective surface is of interest (e.g. to assess the visibility ), then it should be evaluated as in the previous section. In most cases, however, it is not the luminance of the surface that is of interest (which depends on both the reflectivity of the object and the properties of the light source ), only the reflectivity of the object. This is a (mostly) unchangeable property of the object that allows it to be recognized and identified in the environment.
The eye has the ability to automatically separate the properties of objects from those of lighting. If, for example, the illuminance of a scene is halved, the luminance of all surfaces is halved. B. a white object is now not true as gray, but still as white. The eye compares the objects of the entire scene with each other and almost completely “calculates” a change in brightness common to all ( brightness constancy ). In this context, "brightness" is not to be understood as a statement about an "amount of light", but rather a statement about a more or less strong reflectivity of the surface (for example about a "light" vase as opposed to a "dark" one) .
If the brightness of a surface is to be determined as an object property that is independent of the lighting, the perception of the eye must be imitated by comparing this surface with an identically illuminated white surface ( ). This comparison is expressed by the brightness reference value A, i.e. H. the ratio of the light intensities that are reflected from the viewed and from the white surface:
(The factor 100 takes into account that, according to convention, the light reference value should have a maximum value of 100.)
Comparison with the equation for the standard color value
shows that becomes identical to the brightness reference value when the factor is on
is set.
While the brightness (in the sense of the luminance) of light colors is in principle unlimited and the totality of all possible light colors therefore forms an infinitely expanded "color bag" in the color space, the brightness (in the sense of the brightness reference value) of body colors remains limited to a maximum of 100 and is represented by a finite color body in the color space.
Unrelated and related colors
Whether light or body colors make sense to indicate brightness in a given case depends precisely on how a colored surface is perceived:
- as "unrelated color", i.e. H. standing alone or
- as "related color", i.e. H. in connection with other colored surfaces.
Colors from bright light sources (light colors) are mostly perceived as unrelated colors, whereas colors of objects (body colors) are mostly perceived as related colors.
Exceptions:
- Uniform surfaces that are seen against an unlit background are usually perceived as unrelated colors, even if they are illuminated instead of self-luminous surfaces.
- Screen displays of a scene consist of self-luminous areas of color, but are generally perceived as related colors if they represent a collection of objects.
outlook
- The colorimetry deals with the properties of the color stimulus and therefore the properties of physically existing color stimuli .
The detection of these color stimuli by the color receptors of the eye, the preprocessing of these stimuli in the nerve cells of the retina , their recoding and transmission in the optic nerve as well as their processing in the visual cortex of the brain are complex psychophysical processes, at the end of which is color perception . Color perception with its dependence on the observation conditions as well as its contrast and after-effects is subject to much more complex laws than colorimetry. Terms such as hue , color saturation or lightness describe properties of a perceived color, not properties of a color valence.
For example, the “intensity” of a color valence is described by its luminance, but the brightness of the corresponding perceived color is not proportional to the luminance of the triggering color valence. Luminances behave additively (i.e. the luminance of the additive mixture of two color valences is the sum of the luminances of the output valences), whereas brightnesses are not additive. The perceived brightness of a color increases with increasing color saturation, even if the luminance of the color valence that triggers the perception remains constant. ( Helmholtz-Kohlrausch effect )
The following table compares some dimensions for color valences with the corresponding dimensions for perceived colors. The relationship between the two can be very complex.
| Color valence | perceived color |
|---|---|
| Luminance | Brightness (of an unrelated color) |
| Lightness value | Brightness (of a related color) |
| Chromaticity | Hue and saturation |
| same hue wavelength | hue |
| spectral color component | saturation |
- In addition to different primary valences, different geometries can also be used to represent the entirety of the color locations ; the different color spaces are based on this . These are partly non-linearly related to the norm valence space, but exactly three color coordinates are always required.
For example, in Munsell's color system, the coordinates are Hue, Value and Chroma, with the color locations being described in a spherical coordinate system.
In the L * a * b * color space , the color valence is determined as {L *, a *, b *} with brightness (L *), red-green value (a *), blue-yellow value (b *) . The L * coordinate tries to approximate the non-linear relationship between luminance and brightness. - The arrangement of the color types in color tables makes it possible to see the relationships between the color types in the case of additive mixing. In the standard color table, however, the types of color are not arranged “equally spaced by feeling ”. If, for example, two green types of color are perceived by the observer to be "equally different" as two given red types of color, the two green types of color in the standard color table are significantly further apart than the red (see → MacAdam ellipse ). The distance between two types of color in the standard color table therefore does not allow conclusions to be drawn about their perceived similarity. Color spaces like CIELUV or CIELAB are supposed to alleviate this problem.
| term | Site of action | Type of action | Area of Expertise |
|---|---|---|---|
| Color stimulus | Light source | Transport of photons | Development of colors / optics |
| Color valence | Eye ( cone ) | Spectral-specific response of the retina | Optics + physiology |
| Color sensation | brain | Color perception | Physiology / Psychology |
literature
- M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8
- H. Lang: colorimetry. In: Bergmann-Schaefer: Textbook of Experimental Physics. Volume 3: Optics. 10th edition, Walter de Gruyter, Berlin / New York 2004, ISBN 3-11-017081-7
- RWG Hunt: Measuring Color. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1
- G. Wyszecki, WS Stiles: Color Science - Concepts and Methods, Quantitative Data and Formulas. 2nd ed., John Wiley & Sons 1982, ISBN 0-471-02106-7 (Wiley Classics Library Edition, 2000: ISBN 0-471-39918-3 )
- D. Zawischa: colorimetry. Lecture notes ( online )
Web links
- Color matching : Interactive color matching experiment to determine spectral value curves (English, requires Adobe Flash )
- Chromaticity diagrams : Animated projection of the spectral color train from the three-dimensional XYZ space onto the two-dimensional xy color table plane (English, requires Adobe Flash )
Remarks
-
↑ The possible spectral distributions form an infinite-dimensional manifold , the possible color perceptions form only a three-dimensional manifold. In color perception, an infinite number of spectral vectors are always mapped onto a color valence vector.
This is not to be confused with the fact that the eye has a limited ability to distinguish colors , i.e. that very similar colors may not be differentiated by the eye and are therefore perceived as the same. -
↑ Since the sensitivity ranges of the three types of receptors largely overlap, the two light rays mentioned as an example also trigger stimuli in at least one of the other two types of receptors, but here usually stimuli of different strengths. The ratio of the stimulus strengths that a monochromatic light beam triggers in two different types of receptors allows conclusions to be drawn about the position of the light wavelength in the common sensitivity range, but remains unchanged if the light stimulus intensity changes . The ability of the eye to perceive color information separately from brightness information is based on this fact.
The rods used for night vision have a similar sensitivity range as each of the color receptors, but cannot make any differences to other rod types. They deliver brightness, but not color perception. - ↑ This does not mean that metameric colors look the same under all circumstances. In the case of metameric body colors , a change in the illuminating light can destroy the equality; Colors that are metameric for a 2 ° observer may not necessarily be so for a 10 ° observer ; etc.
-
↑ For the additive mixture, for example, the generally applicable rule can be set up: "Green mixed with red results in yellow", without having to take into account which spectral distributions these color stimuli have.
There are generally no such rules for other types of color mixing. For the subtractive color mixing, for example, the rule “blue subtractively mixed with yellow results in green” is often taught. This means that of white light, from which a blue filter has removed the long-wave component and a yellow filter the short-wave component, only the middle wavelengths remain, so the result of the mixture looks green. However, this only applies if both the blue and the yellow filter allow the green wavelengths to pass through, i.e. both have a common pass band . If their pass bands do not overlap, there is no light that can pass through both filters and the result of the mixture is black. It is not only important here that one filter looks blue and one yellow, but also their spectral distributions must be taken into account. - ↑ For a fully color-capable, i.e. trichromatic human eye.
- ↑ The color type is determined by the " hue " and the " color saturation ". (These terms used here for the sake of clarity are in quotation marks because they actually describe properties of color perception and not the properties of the physical color types dealt with here. The correct terms would be “hue of the same wavelength” and “spectral color component” .)
- ↑ Photometric quantities are a quantitative measure for a "light stimulus". Similar to the color stimulus (only without taking the color properties into account) the light stimulus is the physically present radiation that enters the eye. Their quantitative properties can be measured objectively and must not be confused with perceived properties such as brightness, which are usually non-linearly related to the photometric properties of the light stimulus.
- ↑ It is a matter of a distribution density : and thus . It is appropriate for the respective measuring situation radiometric size (for example, beam density , beam intensity or radiation power ).
- ↑ Since the color types contain no information about the brightness, the color type selected as reference should actually be correctly designated as "achromatic" and the point a = 1/3, b = 1/3 in the color table as "achromatic point". In this context, however, it is usually common to speak of the color type “white” and the “white point”.
-
↑ These numerical values are also the luminance coefficients of Abney's law in RGB space. In general, the following applies to a luminance :
- .
- ↑ Since virtual color valences can generally not be visible, it does not make sense to describe them with color vocabulary such as "red" or "green". Formally, however, according to its position in the color table, corresponds to a reddish color valence that is more saturated than any visible red. Corresponds to a green with the hue of the spectral color with a wavelength of 520 nm, but is significantly more saturated than any visible green of this hue. corresponds to a blue with the hue of the spectral color with the wavelength 477 nm, but is much more saturated than any visible blue of this hue (see MacAdam, Color Measurement, p. 12).
- ↑ Most of the complex processing mechanisms that are necessary for this perceptual performance do not take place in the eye itself. The term “eye” is only used here as an abbreviation for the entire perception apparatus involved.
- ↑ In the case of luminescent surfaces, the brightness reference value can also be greater than 100.
- ↑ Nevertheless, for the sake of brevity, but actually incorrectly, the term "brightness of a color valence" is often used - as in this article.
Individual evidence
- ↑ E. Scheibner, E. Wolf: Psychophysics and physiology of color seeing. In: H.-W. Bodmann (Hrsg.): Aspects of information processing - function of the visual system and technical image presentation. Springer, Berlin / Heidelberg / New York / Tokyo 1985, ISBN 978-3-540-15725-0 , p. 5: “With additive color mixing, all that matters is the appearance of the color stimuli. Classes of such color stimuli that look the same, called 'color valences' in German standards (DIN 5033, 1979), are thus the objects of additive color mixing and therefore the elements of the instrumental color space concerned […]. "
- ^ H. Lang: Colorimetry. In: Bergmann-Schaefer: Textbook of Experimental Physics. Volume 3: Optics. 10th edition, de Gruyter, Berlin / New York 2004, ISBN 3-11-017081-7 , p. 707: “The relation between color stimuli and color valences is irreversibly clear. Rather, the color comparison defines a method with which the color stimuli can be combined into classes of color stimuli that look the same. Each class of color stimuli that look the same forms a color valence. "
- ↑ M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8 , p. 30
- ↑ M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8 , pp. 9, 31
- ^ H. Lang: Colorimetry. In: Bergmann-Schaefer: Textbook of Experimental Physics. Volume 3: Optics. 10th edition, de Gruyter, Berlin / New York 2004, ISBN 3-11-017081-7 , p. 706
- ↑ a b c H. Lang: color metrics. In: Bergmann-Schaefer: Textbook of Experimental Physics. Volume 3: Optics. 10th edition, de Gruyter, Berlin / New York 2004, ISBN 3-11-017081-7 , p. 707
- ↑ M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8 , p. 31
- ↑ M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8 , p. 23
- ↑ M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8 , p. 22
- ↑ M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8 , p. 75
- ↑ M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8 , p. 76
- ^ RWG Hunt: Measuring Color. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1 , p. 39
- ↑ M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8 , p. 238
- ^ DL MacAdam: Color Measurement - Theme and Variations. 2nd ed., Springer, Berlin Heidelberg 1985, ISBN 978-3-540-15573-7 , p. 10
- ↑ a b G. Wyszecki, WS Stiles: Color Science - Concepts and Methods, Quantitative Data and Formulas. 2nd ed., John Wiley & Sons 1982, ISBN 0-471-02106-7 (Wiley Classics Library Edition, 2000: ISBN 0-471-39918-3 ), p. 134
- ↑ J. Schanda (Ed.): Colorimetry - Understanding the CIE System. John Wiley & Sons, Hoboken NY 2007, ISBN 978-0-470-04904-4 , p. 19
- ^ RWG Hunt: Measuring Color. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1 , p. 40 (divided by 5.6508 to get the numerical values that also occur in the transformation matrix RGB → XYZ)
- ↑ G. Wyszecki, WS Stiles: Color Science - Concepts and Methods, Quantitative Data and Formulas. 2nd ed., John Wiley & Sons 1982, ISBN 0-471-02106-7 (Wiley Classics Library Edition, 2000: ISBN 0-471-39918-3 ), p. 138
- ↑ G. Wyszecki, WS Stiles: Color Science - Concepts and Methods, Quantitative Data and Formulas. 2nd ed., John Wiley & Sons 1982, ISBN 0-471-02106-7 (Wiley Classics Library Edition, 2000: ISBN 0-471-39918-3 ), p. 132
- ↑ M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8 , p. 71
- ↑ DIN 5033–1: Color measurement - Part 1: Basic concepts of colorimetry, Beuth, Berlin 2009
- ^ RWG Hunt: Measuring Color. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1 , p. 45
- ↑ G. Wyszecki, WS Stiles: Color Science - Concepts and Methods, Quantitative Data and Formulas. 2nd ed., John Wiley & Sons 1982, ISBN 0-471-02106-7 (Wiley Classics Library Edition, 2000: ISBN 0-471-39918-3 ), p. 131
- ↑ M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8 , p. 108
- ↑ a b H. Lang: color metrics. In: Bergmann-Schaefer: Textbook of Experimental Physics. Volume 3: Optics. 10th edition, de Gruyter, Berlin / New York 2004, ISBN 3-11-017081-7 , p. 724
- ↑ a b R.WG Hunt: Measuring Color. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1 , p. 210
- ^ RWG Hunt: Measuring Color. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1 , p. 193
- ↑ a b c How to interpret the sRGB color space (specified in IEC 61966-2-1) for ICC profiles ( PDF , accessed on October 14, 2015)
- ^ RWG Hunt: Measuring Color. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1 , p. 47
- ↑ J. Schanda (Ed.): Colorimetry - Understanding the CIE System. John Wiley & Sons, Hoboken NY 2007, ISBN 978-0-470-04904-4 , p. 39
- ↑ M. Richter: Introduction to colorimetry. 2nd edition, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8 , p. 116
- ↑ G. Wyszecki, WS Stiles: Color Science - Concepts and Methods, Quantitative Data and Formulas. 2nd ed., John Wiley & Sons 1982, ISBN 0-471-02106-7 (Wiley Classics Library Edition, 2000: ISBN 0-471-39918-3 ), p. 157
- ↑ a b R.WG Hunt: Measuring Color. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1 , p. 27
- ↑ International Electrotechnical Commission (IEC): International Electrotechnical Vocabulary , ref. 845-02-35, hue : hue, hue: property of a visual sensation according to which a surface appears to be similar to one of the perceived colors red, yellow, green and blue or a combination of two thereof. ("Hue: attribute of a visual sensation according to which an area appears to be similar to one of the perceived colors, red, yellow, green, and blue, or to a combination of two of them."), Accessed on 28. October 2015.
- ↑ International Electrotechnical Commission (IEC): International Electrotechnical Vocabulary , ref. 845-02-41, saturation : saturation: the chroma of a surface, assessed in relation to its brightness. ("Saturation: chromaticness, colorfulness, of an area judged in proportion to its brightness."), Accessed on October 28, 2015.
- ↑ International Electrotechnical Commission (IEC): International Electrotechnical Vocabulary , ref. 845-02-28, brightness : Brightness: property of a visual sensation according to which a surface appears to emit more or less light. ("Brightness: attribute of a visual sensation according to which an area appears to emit more or less light."), Accessed October 28, 2015.
- ^ RWG Hunt: Measuring Color. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1 , p. 38
- ^ RWG Hunt: Measuring Color. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1 , p. 36
- ^ RWG Hunt: Measuring Color. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1 , p. 69