3: Difference between revisions

← 2 3 4 →
−1 0 1 2 3 4 5 6 7 8 9 → List of numbers; Integers; ← 0 10 20 30 40 50 60 70 80 90 →
Cardinal	three
Ordinal	3rd; (third)
Numeral system	ternary
Factorization	prime
Prime	2nd
Divisors	1, 3
Greek numeral	Γ´
Roman numeral	III, iii
Greek prefix	tri-
Latin prefix	tre-/ter-
Binary	112
Ternary	103
Senary	36
Octal	38
Duodecimal	312
Hexadecimal	316
Arabic, Kurdish, Persian, Sindhi, Urdu	٣
Bengali, Assamese	৩
Chinese	三，弎，叄
Devanāgarī	३
Ge'ez	፫
Greek	γ (or Γ)
Hebrew	ג
Japanese	三/参
Khmer	៣
Armenian	Գ
Malayalam	൩
Tamil	௩
Telugu	౩
Kannada	೩
Thai	๓
N'Ko	߃
Lao	໓
Georgian	Ⴂ/ⴂ/გ (Gani)
Babylonian numeral	𒐗
Maya numerals	•••
Morse code	... _ _

Browse history interactively

← Previous edit

Content deleted Content added

VisualWikitext

Inline

Latest revision as of 11:39, 19 May 2024

3 (three) is a number, numeral and digit. It is the natural number following 2 and preceding 4, and is the smallest odd prime number and the only prime preceding a square number. It has religious and cultural significance in many societies.

Evolution of the Arabic digit[edit]

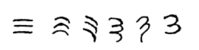
The use of three lines to denote the number 3 occurred in many writing systems, including some (like Roman and Chinese numerals) that are still in use. That was also the original representation of 3 in the Brahmic (Indian) numerical notation, its earliest forms aligned vertically.^[1] However, during the Gupta Empire the sign was modified by the addition of a curve on each line. The Nāgarī script rotated the lines clockwise, so they appeared horizontally, and ended each line with a short downward stroke on the right. In cursive script, the three strokes were eventually connected to form a glyph resembling a ⟨3⟩ with an additional stroke at the bottom: ३.

The Indian digits spread to the Caliphate in the 9th century. The bottom stroke was dropped around the 10th century in the western parts of the Caliphate, such as the Maghreb and Al-Andalus, when a distinct variant ("Western Arabic") of the digit symbols developed, including modern Western 3. In contrast, the Eastern Arabs retained and enlarged that stroke, rotating the digit once more to yield the modern ("Eastern") Arabic digit "٣".^[2]

In most modern Western typefaces, the digit 3, like the other decimal digits, has the height of a capital letter, and sits on the baseline. In typefaces with text figures, on the other hand, the glyph usually has the height of a lowercase letter "x" and a descender: "". In some French text-figure typefaces, though, it has an ascender instead of a descender.

A common graphic variant of the digit three has a flat top, similar to the letter Ʒ (ezh). This form is sometimes used to prevent falsifying a 3 as an 8. It is found on UPC-A barcodes and standard 52-card decks.

Mathematics[edit]

According to Pythagoras and the Pythagorean school, the number 3, which they called triad, is the only number to equal the sum of all the terms below it, and the only number whose sum with those below equals the product of them and itself.^[3]

Divisibility rule[edit]

A natural number is divisible by three if the sum of its digits in base 10 is divisible by 3. For example, the number 21 is divisible by three (3 times 7) and the sum of its digits is 2 + 1 = 3. Because of this, the reverse of any number that is divisible by three (or indeed, any permutation of its digits) is also divisible by three. For instance, 1368 and its reverse 8631 are both divisible by three (and so are 1386, 3168, 3186, 3618, etc.). See also Divisibility rule. This works in base 10 and in any positional numeral system whose base divided by three leaves a remainder of one (bases 4, 7, 10, etc.).

Properties of the number[edit]

3 is the second smallest prime number and the first odd prime number. It is the first unique prime, such that the period length value of 1 of the decimal expansion of its reciprocal, 0.333..., is unique. 3 is a twin prime with 5, and a cousin prime with 7, and the only known number $n$ such that $n$ ! − 1 and $n$ ! + 1 are prime, as well as the only prime number $p$ such that $p$ − 1 yields another prime number, 2. A triangle is made of three sides. It is the smallest non-self-intersecting polygon and the only polygon not to have proper diagonals. When doing quick estimates, 3 is a rough approximation of $π$ , 3.1415..., and a very rough approximation of e, 2.71828...

3 is the first Mersenne prime, as well as the second Mersenne prime exponent and the second double Mersenne prime exponent, for 7 and 127, respectively. 3 is also the first of five known Fermat primes, which include 5, 17, 257, and 65537. It is the second Fibonacci prime (and the second Lucas prime), the second Sophie Germain prime, the third Harshad number in base 10, and the second factorial prime, as it is equal to 2! + 1.

3 is the second and only prime triangular number, and Gauss proved that every integer is the sum of at most 3 triangular numbers.

Three is the only prime which is one less than a perfect square. Any other number which is $n^{2}$ − 1 for some integer $n$ is not prime, since it is ( $n$ − 1)( $n$ + 1). This is true for 3 as well (with $n$ = 2), but in this case the smaller factor is 1. If $n$ is greater than 2, both $n$ − 1 and $n$ + 1 are greater than 1 so their product is not prime.

Related properties[edit]

The trisection of the angle was one of the three famous problems of antiquity.

3 is the number of non-collinear points needed to determine a plane, a circle, and a parabola.

There are only three distinct 4×4 panmagic squares.

Three of the five Platonic solids have triangular faces – the tetrahedron, the octahedron, and the icosahedron. Also, three of the five Platonic solids have vertices where three faces meet – the tetrahedron, the hexahedron (cube), and the dodecahedron. Furthermore, only three different types of polygons comprise the faces of the five Platonic solids – the triangle, the square, and the pentagon.

There are three finite convex uniform polytope groups in three dimensions, aside from the infinite families of prisms and antiprisms: the tetrahedral group, the octahedral group, and the icosahedral group. In dimensions $n$ ⩾ 5, there are only three regular polytopes: the $n$ -simplexes, $n$ -cubes, and $n$ -orthoplexes. In dimensions $n$ ⩾ 9, the only three uniform polytope families, aside from the numerous infinite proprismatic families, are the $\mathrm {A} _{n}$ simplex, $\mathrm {B} _{n}$ cubic, and $\mathrm {D} _{n}$ demihypercubic families. For paracompact hyperbolic honeycombs, there are three groups in dimensions 6 and 9, or equivalently of ranks 7 and 10, with no other forms in higher dimensions. Of the final three groups, the largest and most important is ${\bar {T}}_{9}$ , that is associated with an important Kac–Moody Lie algebra $\mathrm {E} _{10}$ .^[4]

Numeral systems[edit]

There is some evidence to suggest that early man may have used counting systems which consisted of "One, Two, Three" and thereafter "Many" to describe counting limits. Early peoples had a word to describe the quantities of one, two, and three but any quantity beyond was simply denoted as "Many". This is most likely based on the prevalence of this phenomenon among people in such disparate regions as the deep Amazon and Borneo jungles, where western civilization's explorers have historical records of their first encounters with these indigenous people.^[5]

List of basic calculations[edit]

Multiplication	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	50	100	1000	10000
3 × x	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60	63	66	69	72	75	150	300	3000	30000

Division	1	2	3	4	5	6	7	8	9	10		11	12	13	14	15	16	17	18	19	20
3 ÷ x	3	1.5	1	0.75	0.6	0.5	0.428571	0.375	0.3	0.3		0.27	0.25	0.230769	0.2142857	0.2	0.1875	0.17647058823529411	0.16	0.157894736842105263	0.15
x ÷ 3	0.3	0.6	1	1.3	1.6	2	2.3	2.6	3	3.3		3.6	4	4.3	4.6	5	5.3	5.6	6	6.3	6.6

Exponentiation	1	2	3	4	5	6	7	8	9	10		11	12	13	14	15	16	17	18	19	20
3^x	3	9	27	81	243	729	2187	6561	19683	59049		177147	531441	1594323	4782969	14348907	43046721	129140163	387420489	1162261467	3486784401
x³	1	8	27	64	125	216	343	512	729	1000		1331	1728	2197	2744	3375	4096	4913	5832	6859	8000

Science[edit]

Three is the atomic number of lithium.
Three is the number of dimensions that humans can perceive. Humans perceive the universe to have three spatial dimensions, but some theories, such as string theory, suggest there are more.^{[citation needed]}
Three is the number of elementary fermion generations according to the Standard Model of particle physics.^[6]
In particle physics, each proton or neutron is composed of three quarks.^[7]
There are three primary colors in the additive and subtractive models.
The ability of the human eye to distinguish colors is based upon the varying sensitivity of different cells in the retina to light of different wavelengths. Humans being trichromatic, the retina contains three types of color receptor cells, or cones.^{[citation needed]}
In physics, three-body problems have no general closed-form solution, unlike two-body problems.^[8]

Engineering[edit]

The triangle, a polygon with three edges and three vertices, is the most stable physical shape. For this reason it is widely utilized in construction, engineering and design.^[9]

Protoscience[edit]

In European alchemy, the three primes (Latin: tria prima) were salt (), sulfur () and mercury (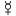).^[10]^[11]
The three doshas (weaknesses) and their antidotes are the basis of Ayurvedic medicine in India.^{[citation needed]}

Pseudoscience[edit]

Three is the symbolic representation for Mu, Augustus Le Plongeon's and James Churchward's lost continent.^[12]

Philosophy[edit]

Philosophers such as Aquinas, Kant, Hegel, C. S. Peirce, and Karl Popper have made threefold divisions, or trichotomies, which have been important in their work.^{[citation needed]}
Hegel's dialectic of Thesis + Antithesis = Synthesis creates three-ness from two-ness.^{[citation needed]}

Religion[edit]

Symbol of the Triple Goddess showing the waxing, full and waning Moon

Many world religions contain triple deities or concepts of trinity, including the Hindu Trimurti and Tridevi, the Triglav (lit. "Three-headed one"), the chief god of the slavs, the three Jewels of Buddhism, the three Pure Ones of Taoism, the Christian Holy Trinity, and the Triple Goddess of Wicca.

The Shield of the Trinity is a diagram of the Christian doctrine of the Trinity.

Christianity[edit]

The threefold office of Christ is a Christian doctrine which states that Christ performs the functions of prophet, priest, and king.
During the Agony in the Garden, Christ asked three times for the cup to be taken from him.
Jesus rose from the dead on the third day after his death.
The devil tempted Jesus three times.
Saint Peter thrice denied Jesus and thrice affirmed his faith in Jesus.
The Magi – wise men who were astronomers/astrologers from Persia^{[citation needed]} – gave Jesus three gifts.^[13]^[14]
There are three Synoptic Gospels and three epistles of John.
Paul the Apostle went blind for three days after his conversion to Christianity.

Judaism[edit]

Noah had three sons: Ham, Shem and Japheth
The Three Patriarchs: Abraham, Isaac and Jacob
The prophet Balaam beat his donkey three times.
The prophet Jonah spent three days and nights in the belly of a large fish
Three divisions of the Written Torah: Torah (Five Books of Moses), Nevi'im (Prophets), Ketuvim (Writings)^[15]
Three divisions of the Jewish people: Kohen, Levite, Yisrael
Three daily prayers: Shacharit, Mincha, Maariv
Three Shabbat meals
Shabbat ends when three stars are visible in the night sky^[16]
Three Pilgrimage Festivals: Passover, Shavuot, Sukkot
Three matzos on the Passover Seder table^[17]
The Three Weeks, a period of mourning bridging the fast days of Seventeenth of Tammuz and Tisha B'Av
Three cardinal sins for which a Jew must die rather than transgress: idolatry, murder, sexual immorality^[18]
Upsherin, a Jewish boy's first haircut at age 3^[19]
A Beth din is composed of three members
Potential converts are traditionally turned away three times to test their sincerity^[20]
In the Jewish mystical tradition of the Kabbalah, it is believed that the soul consists of three parts, with the highest being neshamah ("breath"), the middle being ruach ("wind" or "spirit") and the lowest being nefesh ("repose").^[21] Sometimes the two elements of Chayah ("life" or "animal") and Yechidah ("unit") are additionally mentioned.
In the Kabbalah, the Tree of Life (Hebrew: Etz ha-Chayim, עץ החיים) refers to a latter 3-pillar diagrammatic representation of its central mystical symbol, known as the 10 Sephirot.

Islam[edit]

The three core principles in Shia tradition: Tawhid (Oneness of God), Nabuwwa (Concept of Prophethood), Imama (Concept of Imam)

Buddhism[edit]

The Triple Bodhi (ways to understand the end of birth) are Budhu, Pasebudhu, and Mahaarahath.
The Three Jewels, the three things that Buddhists take refuge in.

Shinto[edit]

The Imperial Regalia of Japan of the sword, mirror, and jewel.

Daoism[edit]

The Three Treasures (Chinese: 三寶; pinyin: sānbǎo; Wade–Giles: san-pao), the basic virtues in Taoism.
The Three Dantians
Three Lines of a Trigram
Three Sovereigns: Heaven Fu Xi (Hand – Head – 3º Eye), Humanity Shen Nong (Unit 69), Hell Nüwa (Foot – Abdomen – Umbiculus).

Hinduism[edit]

The Trimurti: Brahma the Creator, Vishnu the Preserver, and Shiva the Destroyer.
The three guṇas (triguna) found in the Samkhya school of Hindu philosophy.^[22]
The three paths to salvation in the Bhagavad Gita named Karma Yoga, Bhakti Yoga and Jnana Yoga.

Zoroastrianism[edit]

The three virtues of Humata, Hukhta and Huvarshta (Good Thoughts, Good Words and Good Deeds) are a basic tenet in Zoroastrianism.

Norse mythology[edit]

Three is a very significant number in Norse mythology, along with its powers 9 and 27.

Prior to Ragnarök, there will be three hard winters without an intervening summer, the Fimbulwinter.
Odin endured three hardships upon the World Tree in his quest for the runes: he hanged himself, wounded himself with a spear, and suffered from hunger and thirst.
Bor had three sons, Odin, Vili, and Vé.

Other religions[edit]

The Wiccan Rule of Three.
The Triple Goddess: Maiden, Mother, Crone; the three fates.
The sons of Cronus: Zeus, Poseidon, and Hades.
The Slavic god Triglav has three heads.

Esoteric tradition[edit]

The Theosophical Society has three conditions of membership.
Gurdjieff's Three Centers and the Law of Three.
Liber AL vel Legis, the central scripture of the religion of Thelema, consists of three chapters, corresponding to three divine narrators respectively: Nuit, Hadit and Ra-Hoor-Khuit.
The Triple Greatness of Hermes Trismegistus is an important theme in Hermeticism.

As a lucky or unlucky number[edit]

Three (三, formal writing: 叁, pinyin sān, Cantonese: saam¹) is considered a good number in Chinese culture because it sounds like the word "alive" (生 pinyin shēng, Cantonese: saang¹), compared to four (四, pinyin: sì, Cantonese: sei¹), which sounds like the word "death" (死 pinyin sǐ, Cantonese: sei²).

Counting to three is common in situations where a group of people wish to perform an action in synchrony: Now, on the count of three, everybody pull! Assuming the counter is proceeding at a uniform rate, the first two counts are necessary to establish the rate, and the count of "three" is predicted based on the timing of the "one" and "two" before it. Three is likely used instead of some other number because it requires the minimal amount counts while setting a rate.

There is another superstition that it is unlucky to take a third light, that is, to be the third person to light a cigarette from the same match or lighter. This superstition is sometimes asserted to have originated among soldiers in the trenches of the First World War when a sniper might see the first light, take aim on the second and fire on the third.^{[citation needed]}

The phrase "Third time's the charm" refers to the superstition that after two failures in any endeavor, a third attempt is more likely to succeed. This is also sometimes seen in reverse, as in "third man [to do something, presumably forbidden] gets caught". ^{[citation needed]}

Luck, especially bad luck, is often said to "come in threes".^[23]

Film[edit]

A number of film versions of the novel The Three Musketeers by Alexandre Dumas: (1921, 1933, 1948, 1973, 1992, 1993 and 2011).
3 Days of the Condor (1975), starring Robert Redford, Faye Dunaway, Cliff Robertson, and Max von Sydow.
Three Amigos (1986), comedy film starring Steve Martin, Chevy Chase, and Martin Short.
Three Kings (1999), starring George Clooney, Mark Wahlberg, Ice Cube, and Spike Jonze.
3 Days to Kill (2014), starring Kevin Costner.
Three Billboards Outside Ebbing, Missouri (2017), starring Frances McDormand, Woody Harrelson, Sam Rockwell.

References[edit]

^ Smith, David Eugene; Karpinski, Louis Charles (1911). The Hindu-Arabic numerals. Boston; London: Ginn and Company. pp. 27–29, 40–41.
^ Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer transl. David Bellos et al. London: The Harvill Press (1998): 393, Fig. 24.63
^ Priya Hemenway (2005), Divine Proportion: Phi In Art, Nature, and Science, Sterling Publishing Company Inc., pp. 53–54, ISBN 1-4027-3522-7
^ Allcock, Daniel (May 2018). "Prenilpotent Pairs in the E10 root lattice" (PDF). Mathematical Proceedings of the Cambridge Philosophical Society. 164 (3): 473–483. Bibcode:2018MPCPS.164..473A. doi:10.1017/S0305004117000287. S2CID 8547735. Archived (PDF) from the original on 2022-11-03. Retrieved 2022-11-03.
"The details of the previous section were E10-specific, but the same philosophy looks likely to apply to the other symmetrizable hyperbolic root systems...it seems valuable to give an outline of how the calculations would go", regarding E10 as a model example of symmetrizability of other root hyperbolic E_n systems.
^ Gribbin, Mary; Gribbin, John R.; Edney, Ralph; Halliday, Nicholas (2003). Big numbers. Cambridge: Wizard. ISBN 1840464313.
^ Harari, H. (1977). "Three generations of quarks and leptons" (PDF). In van Goeler, E.; Weinstein, R. (eds.). Proceedings of the XII Rencontre de Moriond. p. 170. SLAC-PUB-1974.
^ Adair, R.K. (1989). The Great Design: Particles, Fields, and Creation. Oxford University Press. p. 214. Bibcode:1988gdpf.book.....A.
^ Barrow-Green, June (2008). "The Three-Body Problem". In Gowers, Timothy; Barrow-Green, June; Leader, Imre (eds.). The Princeton Companion to Mathematics. Princeton University Press. pp. 726–728.
^ "Most stable shape- triangle". Maths in the city. Retrieved February 23, 2015.
^ Eric John Holmyard. Alchemy. 1995. p.153
^ Walter J. Friedlander. The golden wand of medicine: a history of the caduceus symbol in medicine. 1992. p.76-77
^ Churchward, James (1931). "The Lost Continent of Mu – Symbols, Vignettes, Tableaux and Diagrams". Biblioteca Pleyades. Archived from the original on 2015-07-18. Retrieved 2016-03-15.
^ "Encyclopaedia Britannica". Lexikon des Gesamten Buchwesens Online (in German). doi:10.1163/9789004337862_lgbo_com_050367.
^ T. E. T. (25 January 1877). "The Encyclopaedia Britannica". Nature. XV (378): 269–271. Archived from the original on 24 July 2020. Retrieved 12 July 2019.
^ Marcus, Rabbi Yossi (2015). "Why are many things in Judaism done three times?". Ask Moses. Archived from the original on 2 April 2015. Retrieved 16 March 2015.
^ "Shabbat". Judaism 101. 2011. Archived from the original on 29 June 2009. Retrieved 16 March 2015.
^ Kitov, Eliyahu (2015). "The Three Matzot". Chabad.org. Archived from the original on 24 March 2015. Retrieved 16 March 2015.
^ Kaplan, Rabbi Aryeh (28 August 2004). "Judaism and Martyrdom". Aish.com. Archived from the original on 20 March 2015. Retrieved 16 March 2015.
^ "The Basics of the Upsherin: A Boy's First Haircut". Chabad.org. 2015. Archived from the original on 22 March 2015. Retrieved 16 March 2015.
^ "The Conversion Process". Center for Conversion to Judaism. Archived from the original on 23 February 2021. Retrieved 16 March 2015.
^ Kaplan, Aryeh. "The Soul Archived 2015-02-24 at the Wayback Machine". Aish. From The Handbook of Jewish Thought (Vol. 2, Maznaim Publishing. Reprinted with permission.) September 4, 2004. Retrieved February 24, 2015.
^ James G. Lochtefeld, Guna, in The Illustrated Encyclopedia of Hinduism: A-M, Vol. 1, Rosen Publishing, ISBN 978-0-8239-3179-8, page 265
^ See "bad Archived 2009-03-02 at the Wayback Machine" in the Oxford Dictionary of Phrase and Fable, 2006, via Encyclopedia.com.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers London: Penguin Group. (1987): 46–48

External links[edit]

Tricyclopedic Book of Threes by Michael Eck
Threes in Human Anatomy by John A. McNulty
Grime, James. "3 is everywhere". Numberphile. Brady Haran. Archived from the original on 2013-05-14. Retrieved 2013-04-13.
The Number 3
The Positive Integer 3
Prime curiosities: 3

[Smith_Karpinski_1911-1] Smith, David Eugene; Karpinski, Louis Charles (1911). The Hindu-Arabic numerals. Boston; London: Ginn and Company. pp. 27–29, 40–41.

[2] Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer transl. David Bellos et al. London: The Harvill Press (1998): 393, Fig. 24.63

[3] Priya Hemenway (2005), Divine Proportion: Phi In Art, Nature, and Science, Sterling Publishing Company Inc., pp. 53–54, ISBN 1-4027-3522-7

[4] Allcock, Daniel (May 2018). "Prenilpotent Pairs in the E10 root lattice" (PDF). Mathematical Proceedings of the Cambridge Philosophical Society. 164 (3): 473–483. Bibcode:2018MPCPS.164..473A. doi:10.1017/S0305004117000287. S2CID 8547735. Archived (PDF) from the original on 2022-11-03. Retrieved 2022-11-03.
"The details of the previous section were E10-specific, but the same philosophy looks likely to apply to the other symmetrizable hyperbolic root systems...it seems valuable to give an outline of how the calculations would go", regarding E10 as a model example of symmetrizability of other root hyperbolic E_n systems.

[5] Gribbin, Mary; Gribbin, John R.; Edney, Ralph; Halliday, Nicholas (2003). Big numbers. Cambridge: Wizard. ISBN 1840464313.

[6] Harari, H. (1977). "Three generations of quarks and leptons" (PDF). In van Goeler, E.; Weinstein, R. (eds.). Proceedings of the XII Rencontre de Moriond. p. 170. SLAC-PUB-1974.

[7] Adair, R.K. (1989). The Great Design: Particles, Fields, and Creation. Oxford University Press. p. 214. Bibcode:1988gdpf.book.....A.

[8] Barrow-Green, June (2008). "The Three-Body Problem". In Gowers, Timothy; Barrow-Green, June; Leader, Imre (eds.). The Princeton Companion to Mathematics. Princeton University Press. pp. 726–728.

[9] "Most stable shape- triangle". Maths in the city. Retrieved February 23, 2015.

[Eric_John_Holmyard_1990._p.153-10] Eric John Holmyard. Alchemy. 1995. p.153

[11] Walter J. Friedlander. The golden wand of medicine: a history of the caduceus symbol in medicine. 1992. p.76-77

[Three_is_for_the_Lost_Continent_of_Mu-12] Churchward, James (1931). "The Lost Continent of Mu – Symbols, Vignettes, Tableaux and Diagrams". Biblioteca Pleyades. Archived from the original on 2015-07-18. Retrieved 2016-03-15.

[13] "Encyclopaedia Britannica". Lexikon des Gesamten Buchwesens Online (in German). doi:10.1163/9789004337862_lgbo_com_050367.

[14] T. E. T. (25 January 1877). "The Encyclopaedia Britannica". Nature. XV (378): 269–271. Archived from the original on 24 July 2020. Retrieved 12 July 2019.

[why-15] Marcus, Rabbi Yossi (2015). "Why are many things in Judaism done three times?". Ask Moses. Archived from the original on 2 April 2015. Retrieved 16 March 2015.

[16] "Shabbat". Judaism 101. 2011. Archived from the original on 29 June 2009. Retrieved 16 March 2015.

[17] Kitov, Eliyahu (2015). "The Three Matzot". Chabad.org. Archived from the original on 24 March 2015. Retrieved 16 March 2015.

[18] Kaplan, Rabbi Aryeh (28 August 2004). "Judaism and Martyrdom". Aish.com. Archived from the original on 20 March 2015. Retrieved 16 March 2015.

[19] "The Basics of the Upsherin: A Boy's First Haircut". Chabad.org. 2015. Archived from the original on 22 March 2015. Retrieved 16 March 2015.

[20] "The Conversion Process". Center for Conversion to Judaism. Archived from the original on 23 February 2021. Retrieved 16 March 2015.

[21] Kaplan, Aryeh. "The Soul Archived 2015-02-24 at the Wayback Machine". Aish. From The Handbook of Jewish Thought (Vol. 2, Maznaim Publishing. Reprinted with permission.) September 4, 2004. Retrieved February 24, 2015.

[22] James G. Lochtefeld, Guna, in The Illustrated Encyclopedia of Hinduism: A-M, Vol. 1, Rosen Publishing, ISBN 978-0-8239-3179-8, page 265

[23] See "bad Archived 2009-03-02 at the Wayback Machine" in the Oxford Dictionary of Phrase and Fable, 2006, via Encyclopedia.com.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]