Infrared spectroscopy
Infrared spectroscopy , short IR spectroscopy and up into the 1960s, infrared spectroscopy called, is a physical method of analysis , which with infrared radiation (wavelength: 800 nm to 1 mm) works. The process is one of the methods of molecular spectroscopy that are based on the excitation of energy states in molecules.
IR spectroscopy is used for the quantitative determination of known substances, which are identified using a reference spectrum, or for the structure elucidation of unknown substances.
Similar molecular spectroscopy methods are Raman spectroscopy , which also provides vibration information in the infrared range, and UV / VIS spectroscopy in the higher frequency range.
Nowadays, Fourier transform infrared spectrometers (FTIR spectrometers) are mainly used. Compared to the dispersive spectrometers used in the past, these offer some decisive advantages. For example, FTIR spectrometers have a significantly higher signal-to-noise ratio and require significantly shorter measurement times. Infrared spectroscopy results are shown in infrared spectrography.
variants
From a spectroscopic point of view, a distinction is made between the near infrared (NIR; wave number : 12500–4000 cm −1 ; wavelength: 0.8–2.5 µm, see near infrared spectroscopy ), the medium or classic (normal) infrared (MIR; wave number: 4000 –400 cm −1 wavelength: 2.5–25 µm) and the far infrared (FIR; wave number: 400–10 cm −1 ; wavelength: 25–1000 µm), since different phenomena can be observed due to the absorption in the respective area are. An absorption in the FIR range mainly leads to the rotation of whole molecules. In the MIR range and NIR range, the oscillation of atoms or groups of atoms is excited at their molecular bonds, with the so-called harmonics of the MIR range being detectable in the NIR range (especially of CH, OH and NH bonds).
Mid-infrared spectroscopy - often just referred to as IR spectroscopy - is a powerful technique in the chemical analysis of organic substances. It enables direct statements to be made about the presence and possibly the concentration of infrared-active functional groups . The near-infrared spectroscopy (NIRS) is (often, especially in applications for rapid review of substances and mixtures process analysis ) used, but to computerized chemometric models rely with accompanying, randomly incorrect reference analysis.
In IR spectra, in contrast to UV spectra, it is often not the absorption but rather the transmission that is used as a measure of the permeability of the excitation radiation . The transmission is plotted on the vertical axis, increasing upwards - areas of low transmission of the IR radiation result in a downward deflection. However, the representation as an absorption spectrum is also used, especially with ATR technology.
Measuring principle
Absorption of IR radiation
When a substance is irradiated with electromagnetic waves , certain frequency ranges are absorbed. In terms of energy, infrared radiation lies in the range of the rotational levels of small molecules and the vibration levels of molecular bonds, i.e. That is, the absorption causes the bonds to vibrate . They are visible in the form of deflections in the measured spectrum (diagram). Since the energies or frequencies required for this are characteristic of the respective bonds, materials can also be identified in this way. The IR spectroscopy is therefore structure-clarifying.
Interaction between electromagnetic radiation and the molecule can only occur if there is a moving electrical charge in the molecule. This is always the case when the molecule has either a changeable or an inducible dipole moment (IR-active). In molecules with vibrations symmetrical to the center of symmetry, there are no changes in the dipole moment (IR inactive). Such “forbidden” vibrations are often Raman active .
The simplest case is a diatomic molecule. With polyatomic molecules there is a superposition of fundamental vibrations. Accordingly, one sees a number of absorption bands that need to be interpreted.
Mechanical model
The simplest conceivable model that can be used to explain vibration and rotation excitations is the classic model of the interaction of a permanent electric dipole in an electromagnetic field. Later, better models, such as the quantum mechanical model, can also describe molecules without a permanent dipole moment.
There are attractive and repulsive interactions between the atoms and their neighbors. Therefore the optimal bond distance in the molecule is in the minimum of the potential function. Mechanically, this can be imagined as if the atoms were connected by springs. The force that is needed to deflect a spring is described by Hooke's law of springs . If one brings such a molecule into an electric field, as it exists in a plate capacitor, for example, the molecule will first align itself with its dipole moment along the electric field and secondly increase its bond distance. If alternating voltage is now applied or if the molecule is excited with an electromagnetic wave, the functional groups “hanging” on the bonds begin to vibrate and rotate. The mechanistic model is only of limited use, however, as it does not explain, for example, why only discrete energies are permitted for IR excitation and why molecules without a permanent dipole moment also show IR absorption.
Quantum mechanical model
As in the model of classical mechanics, the basis of the quantum mechanical model of vibration and rotation excitation is the potential function. The minimum of the potential function can be approximated by a parabola. Such a parabola results from the integration of Hooke's spring law.
If a molecule is now excited with electromagnetic radiation, the valence bonds within the molecule can be set in oscillations and rotations if the energy is sufficient to lift it from its ground state into the first excited oscillation state. To determine this energy, the Schrödinger equation for this potential has to be solved. After separating the relative motion of atomic nuclei and electrons ( Born-Oppenheimer approximation ), the solution of the Schrödinger equation results in a relationship between the required energy, the bond strength ( k ) and the reduced mass ( μ ). In contrast to the classical harmonic oscillator, in the quantum mechanical case the vibration energy is quantized by the vibration quantum number v .
Schrödinger equation:
Solution of the Schrödinger equation:
Waveforms
In inorganic and organic substances, mechanical vibrations occur when radiation from the infrared range is absorbed. According to R. Mecke , molecular vibrations can be divided into two types:
- Stretching vibrations (stretching vibrations): vibrations along the bond axis of two atoms or parts of a molecule caused by stretching or compressing the bond
-
Deformation vibrations : vibrations under the deformation of the bond angle
- in the plane (bending / flexing vibrations):
- out of plane (torsional / tilting vibrations) - mostly perpendicular to the plane of the bond
Since molecular vibrations of certain atom groups in the range of 4000–1500 cm −1 are particularly characteristic, IR spectroscopy is suitable for determining certain structural elements, in particular the functional groups of the molecule under investigation.
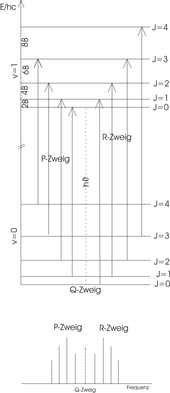
Rotational Vibration Spectrum
The ideal rotation-oscillation spectrum
Hydrogen chloride (HCl) is a diatomic molecule with a pronounced dipole moment. The HCl molecule can be viewed in simplified form as a linear top . As in pure rotation spectroscopy , the rigid rotator model can be used to describe spectra. For a linear molecule the special selection rule for a rotational transition is:
- ,
where represents the rotational quantum number. If the dipole moment is parallel to the main axis of rotation (such as with ammonia ), it would also be possible. For an oscillation transition of the harmonic oscillator, the special selection rule is:
The transitions between different rotational levels ( ) of the vibrational ground state ( ) and rotational levels ( ) of the excited vibrational state ( ) can be used in two groups, the R-branch (right) for transitions and the P-branch (left) for transitions , divided are and are sketched in the figure. Since HCl is not allowed, no Q branch appears. The energy level scheme is shown in the picture above. The length of the arrow clearly shows that each transition is an energy supply of
requires, where is the constant of rotation with the unit . This includes the moment of inertia of the molecule with respect to the axis of rotation.
The following applies to the energy difference to the neighboring transition
Therefore, in the ideal rotational vibration spectrum (lower panel) the peaks have a constant distance of 2 B . In the experiment, the peaks are spaced slightly differently because the model does not:
- the anharmonicity of the vibration
- the expanded atomic distance through centrifugal forces (approximation: rigid rotator )
- and observes the interaction of vibratory and rotational movement.
The real rotation-oscillation spectrum
The real rotation-oscillation spectrum deviates from the ideal due to the limitations of the models used. The distances between the peaks (amplitude deflection in the diagram, also called bands ) are not exactly 2 B , as in the ideal case , but become smaller as the wave number increases in the R branch, but larger in the P branch due to the interaction of rotation and oscillation. The diagram opposite shows a recorded spectrum of hydrogen chloride in the gas phase. In the fine structure of the spectrum, a doubling of all bands due to the two differently inert isotopes of chlorine can be clearly seen.
Position and evaluation of the IR absorption bands
Stronger chemical bonds and atoms of smaller mass cause absorption maxima at large wave numbers (high energy) in the IR spectrum , whereas large masses cause IR absorption maxima at small wave numbers (low energy) (see deuteration ). The energy is proportional to the square of the permanent dipole moment. Therefore, polar molecules provide intense rotational transitions. However, if one compares the amplitudes of the peaks of a single molecule with one another, it is noticeable that the strength of the transitions initially increases rapidly with increasing J , goes through a maximum and finally decreases again for large J. The reason for this is that the strength reflects the degeneracies of the various rotational states and the occupation numbers of the rotational levels in the initial state. The degree of degeneration increases with increasing J , which leads to a higher energy. On the other hand, the occupation numbers decrease with increasing energy, which ultimately leads to a decrease in radiation intensity.
IR spectra are interpreted in order to be able to deduce the molecular shape from the curve of the measured IR spectrum . The different oscillation variants of the molecules are measured and conclusions are drawn about the presence of certain structural elements. A typical IR spectrum ranges from 4000 cm −1 to 400 cm −1 ( wave number ). The wave number is given in the somewhat unusual unit cm −1 . However, this has the advantage that the wave number and the excitation energy are proportional. The wave number multiplied by Planck's quantum and the speed of light gives the energy. In an IR spectrum, each molecule leaves a typical pattern of absorption bands. The length of these bands is usually not evaluated numerically, but only evaluated with attributes such as " strong " or " not very intensive ". From about 1500 cm −1 downwards, the assignment of individual bands to certain molecular vibrations becomes significantly more difficult, as the number of possible overlaps due to framework vibrations becomes very high. This so-called fingerprint area should ideally provide a characteristic spectrum for each type of molecule. In fact, it can be assumed that some differences cannot be represented by the measurement accuracy of the spectral analysis. In this area, however, there are also some bands characteristic of certain structural elements. Pairs of enantiomers show completely identical spectra unless linearly polarized IR light is used. If there are no pure substances but mixtures , the IR spectrum contains information about structural elements of all components of the mixture. With correspondingly high-resolution spectra, however, individual components can still be detected on the basis of characteristic absorptions of certain groups of substances or a combination of several absorptions. Often a direct comparison is made with a spectrum of the pure substance.
The individual assignment of the bands is based on tabulated empirical data. The exact position of a band can be shifted to higher or lower wavenumbers due to the chemical environment of the respective atomic group, which enables further conclusions to be drawn about the proximity of certain structural elements.
| Designation according to Mecke / atomic group | Wave number range in cm −1 |
comment |
|---|---|---|
| ν (–C – H x ) | 2850-3200 | ν = stretching vibration; × = 1… 3, number of bound hydrogen atoms |
| δ (–C – H x ) | 1400 | δ = deformation vibration; × = 1… 3, number of bound hydrogen atoms |
| -C = C | 1650 | |
| –C≡C | 2200-2500 | |
| ν (-OH) | 3200-3600 | In connection with hydrogen bonds, bands often over a large spectral range, for example in the case of liquid water |
| ν (-OH) | 2500-3000 | in carboxy groups |
| -C = O | 1700 | |
| ν (–C≡N) | 2200-2260 | Stretching vibration, e.g. B. in ABS or SAN (see picture) |
| ν (–NH) | 3100-3500 | |
| -NO 2 | 1500 | |
| -C-X | <1500 | where X is a halogen is |
| ν as (O = C = O) | 2349 | Carbon dioxide. |
IR Spectroscopy Techniques
transmission
One of the most commonly used methods is to measure the transmittance of a sample. For this purpose, a sample is irradiated with infrared and the proportion of the measurement radiation that has penetrated the sample is measured. If the sample has IR-active bonds or groups of molecules, areas of lower intensity (absorption bands) can be seen in the transmission spectrum. According to the Lambert-Beer law (among other things), the intensity of the band increases with the sample thickness (it should be noted, however, that this law is generally only approximately valid because it is not compatible with Maxwell's equations Measurement technology more or less large deviations. Detailed explanations and possible solutions can be found in). In addition, part of the radiation is also reflected ; corresponding parts usually have the effect of increased reduced transmission over the entire spectrum and can largely be removed with a baseline correction.
Depending on the shape of the sample (gaseous, liquid, solid), there are special measurement techniques that differ in the type of sample preparation and the measuring cells (sample holder with more or less complicated beam paths). The simplest measuring arrangement corresponds to a simple sample holder that fixes a solid (for example a foil or plate) in the beam path of the spectrometer. In samples with parallel interfaces (such as a film), however, interferences arise from multiple reflections in the sample (see also Newton's rings ) which, depending on the thickness and plane parallelism, falsify the spectrum, but the interference can also be used to determine the layer thickness .
A widely used technique for measuring solid samples is embedding the solid body in an IR-transparent carrier material (also called a matrix). Inorganic salts such as halides of the alkali metals are mainly used ; a common matrix is potassium bromide (KBr). To measure solids, dry potassium bromide powder (KBr is hygroscopic ) is mixed with a little sample substance and intensively ground together. This mixture is then pressed into a tablet in a steel cylinder under vacuum and high mechanical pressure. At this pressure, the potassium bromide becomes plastic and the cold flow (usually also optically) creates transparent “pellets”. These can then simply be placed in the beam path.
Liquid samples can be placed between two IR-transparent plates made from single crystals of alkali metal halides or, rarely, transparent polymer plates. This can be done statically or dynamically in the form of a flow unit. Gaseous samples are usually placed in special cuvettes .
Layer thickness measurement

Polypropylene film with interferences (thickness approx. 38 µm)
|
Since there is interference with plane-parallel thin samples, the actual spectrum is overlaid by a sinusoidal wave train. The thickness of the film can be calculated from the position of the maxima.
with the refractive index of the sample and the number of maxima in the spectral range between the wave numbers and .
You can eliminate the interference in foils by creasing or roughening them.
Christiansen effect
The Christiansen effect (after Christian Christiansen ) is an artifact in IR transmission measurements of substances bound in potassium bromide or another matrix (so-called pellets). It manifests itself primarily through asymmetrical bands in the spectrum. The high-frequency edge shows a very steep course (often higher than the base of the spectrum). The low-frequency flank, on the other hand, shows a rather flat, elongated course. The cause lies in the anomalous dispersion in the vicinity of strong absorption bands . However, the effect is only observed in pellets in which the substance to be examined is too coarse-grained, or in samples with a greater difference in the refractive index between the substance to be examined and the matrix material. This means that the effect can be minimized or prevented if the substance is reduced in size by grinding.
Reflection and absorption
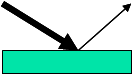
Another method is the (external) reflection of the IR radiation on a smooth surface. The method uses the fact that the reflectance of a sample depends on the complex refractive index of the sample (see Fresnel's formulas ). In the area of the centers of oscillation, the absorption increases, which is represented in the complex refractive index by an increase in the extinction coefficient (the imaginary part of the refractive index). This leads to an increased reflection of the sample for this frequency range and a band in the reflection spectrum.
The technique is suitable, among other things, for the measurement of strongly absorbing samples. The main disadvantage of the method is that the reflection spectra differ greatly from the transmission spectra. The spectra show derivative- like band shapes, the cause of which is the anomalous dispersion in the vicinity of absorption centers of a material, i.e. the refractive index increases here with the wavelength instead of falling as usual. This leads to a changed reflectivity and thus to the distorted bands observed. For pure reflection spectra, the Kramers-Kronig Transformation (KKT) can be used to calculate the absorption spectrum of the sample from the reflection spectra, which enables a better evaluation of the sample. However, this is often only possible to a limited extent.
In addition to the above-described method still further reflection method, especially for existing thin layers is suitable and adsorbates, the so-called technique of " infrared reflection absorption spectroscopy " (Engl .: infrared reflection absorption spectroscopy , IRRAS, also IRAS). Here, infrared radiation is reflected on a metal surface (external) on which the layer to be examined is located. Due to the very high reflectivity of the metal layer (> 90%), the infrared radiation is guided through the sample twice. In addition, similar to surface plasmon resonance spectroscopy , the field is strengthened on the metal surface, which makes the method sensitive even for monolayers , i.e. thin layers with a layer thickness of a few angstroms ; the detection of monolayers is also possible with other measurement techniques of infrared spectroscopy. The measurement is usually carried out at a quasi-grazing incidence, i.e. at an angle of incidence of around 80 ° from the perpendicular. Furthermore, the sensitivity of the method can be increased by using p-polarized radiation .
Diffuse reflection

With diffuse reflection spectroscopy (DRIFTS), rough solids and powders can be examined without pressing the latter into a matrix (see transmission measurements). The infrared beam is directed onto the sample and, due to the rough surface, is no longer directed (like a mirror), but diffusely reflected . The reflected radiation is bundled again by a special mirror arrangement, hemispherical above the sample (see concave mirror ) and guided to the detector.
Due to the diffuse reflection, the radiation components are unevenly distributed and the resulting spectrum has peculiarities that only allow a direct comparison with spectra of other IR technologies to a very limited extent. For an evaluation (qualitative and quantitative), the spectrum can be converted into an absorption spectrum using the Kubelka-Munk function .
Attenuated total internal reflection (ATR)
In ATR infrared spectroscopy, the radiation is guided in total reflection in a reflection element (quasi an optical fiber ) . An evanescent field forms at the interface of the element, the amplitude of which decays exponentially perpendicular to the interface ( evanescent wave ). If there is a sample behind the interface, the evanescent field interacts with the sample, that is, certain frequency ranges can be absorbed by the sample. The absorbed areas are now missing in the spectrum of the reflected beam that is guided to the detector. Since the field decays very quickly, samples for the measurement have to be brought very close to the surface in order to achieve band intensities that can still be evaluated. The measured area usually only covers the first micrometers of the sample. The spectra are similar to those of transmission spectroscopy, but in comparison they have wavelength-dependent intensity differences. This method is suitable for solid and liquid samples.
emission
In the infrared emission spectroscopy (engl. Infrared emission spectroscopy , IRES) of a sample is emitted infrared radiation studied. That means, unlike the previously described methods of absorption spectroscopy, the sample is not irradiated by a high temperature light source and compared with a reference spectrum without a sample, but the sample itself serves as the radiation source. The emission spectra obtained show significantly fewer details with regard to the rotational spectra and the band intensity and shape are more dependent on the temperature.
The measurement of samples without a reference spectrum is possible because a molecule that is in an excited oscillation state can emit infrared radiation with a certain probability . The measured emission bands usually correspond to the transition from an excited to the ground state. The emission can take place both through the presence (through induced emission ) and in the absence (through spontaneous emission ) of incident electromagnetic radiation. However, at room temperature the number of molecules that are in an excited state is relatively small (less than 1% of the number in the ground state, based on a limit value at 1000 cm −1 ) and therefore significantly less than in absorption. In order to get a stronger signal, a sample is usually heated (usually over 100 ° C) and the emitted radiation is measured (see black body ). In addition, based on the product of the Boltzmann factor and the transition probability, only very low radiation energies are to be expected, so that IRE spectroscopy was very complex for a long time and showed only low sensitivity. With improved interferometers and new sensitive detectors, emission spectra can now be recorded routinely.
IRE spectroscopy is used, among other things, to examine paints , molten salts and silicates as well as catalytic reactions on thin layers and adsorbed species on solids. This method offers advantages above all for in-situ measurements at high temperatures, since here, unlike, for example, with reflection techniques, the overlapping of the absorption bands with the emission bands is negligible. Furthermore, IRE spectroscopy can also be used to measure large volumes of gas, for example in process analysis .
Measurements of multiple layers or generally larger volumes can be problematic, since absorption and emission-reabsorption processes take place here and influence the measured spectra. Other parameters influencing the spectrum include the geometry of the sample, the choice of the radiation background, scattered radiation and, as already mentioned, the temperature of the sample itself. For these reasons, even IR emission spectra with a high signal-to-noise ratio are very complex and difficult to evaluate. Various methods have therefore been presented in the literature to compensate for the disturbing influences.
See also
- Surface chemistry
- Alternative ban
- Globar
- Franck-Condon principle
- Journal of Near Infrared Spectroscopy
literature
- Helmut Günzler, Hans-Ulrich Gremlich: IR Spectroscopy: An Introduction . 4th edition. Wiley-VCH, Weinheim 2003, ISBN 978-3-527-30801-9 .
- M. Hesse, H. Meier, B. Zeeh: Spectroscopic methods in organic chemistry . 6th edition. Thieme, Stuttgart 2002, ISBN 3-13-576107-X .
- Bernhard Schrader : Infrared And Raman Spectroscopy . VCH, 1995, ISBN 3-527-26446-9 .
Web links
- Basics and technology of infrared spectroscopy
- Spectral Database for Organic Compounds, SDBS (English)
- Collection of various IR spectra
- IR spectroscopy & Organic Chemistry (English)
- Rotational vibration spectra at Chemgapedia
- ETH Zurich directory of databases and reference works with IR spectra
- ETH Zurich directory of databases and reference works with far-IR spectra
- ETH Zurich directory of databases and reference works with near-IR spectra
Individual evidence
- ↑ BGR infrared spectroscopy. Retrieved July 17, 2008 .
- ↑ Helmut Günzler, Hans-Ulrich Gremlich: IR spectroscopy: An introduction . 4th edition. Wiley-VCH, Weinheim 2003, ISBN 978-3-527-30801-9 , pp. 165-240 .
- ^ Thomas Günter Mayerhöfer, Susanne Pahlow, Jürgen Popp: The Bouguer-Beer-Lambert law: Shining light on the obscure . In: ChemPhysChem . n / a, n / a, July 14, 2020, ISSN 1439-4235 , doi : 10.1002 / cphc.202000464 .
- ↑ C. Christiansen: Investigations into the optical properties of finely divided bodies - first communication . In: Annals of Physics and Chemistry . 23, 1884, pp. 298-306.
- ↑ C. Christiansen: Investigations into the optical properties of finely divided bodies - second communication . In: Annals of Physics and Chemistry . 24, 1885, pp. 439-446.
- ↑ CV Raman : The theory of the Christiansen experiment . In: Proc. Ind. Acad. Sci. 29, 1949, pp. 381-390.
- ↑ Alexander Erlich: Fourier transform infrared spectroscopy. ( Memento of the original from December 11, 2014 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (Examples for IRES spectra; PDF; 2.6 MB), July 8, 2010.
- ↑ a b W. Suetaka: Surface Infrared and Raman Spectroscopy: Methods and Applications . Springer, New York 1995, ISBN 0-306-44963-3 , pp. 163 ff .
- ^ S. Zhang, FS Franke, TM Niemczyk: Emission Spectroscopy . In: Francis Mirabella, Mirabella (Ed.): Modern Techniques in Applied Molecular Spectroscopy . Wiley & Sons, 1998, ISBN 0-471-12359-5 , pp. 323–376 (introduction with descriptions of various techniques).
- ↑ K. Molt: Recording of infrared emission spectra of thin layers on metal surfaces with the help of a computer-coupled grating spectrometer . In: Fresenius' Journal for Analytical Chemistry . tape 308 , no. 4 , 1981, p. 321-326 , doi : 10.1007 / BF00516246 (with reference to G. Herzberg: Spectra of diatomic molecules. Van Nostrand, Princeton 1950.).
- ^ Francis M. Mirabella: Modern techniques in applied molecular spectroscopy . Wiley-IEEE, 1998, ISBN 978-0-471-12359-0 , 9th Emission Spectroscopy, pp. 323-377 .