Geometric focus

The geometric center of gravity or center of gravity of a geometric figure (for example a circular arc , triangle , cone ) is a particularly distinctive point that is interpreted as a kind of center point , even with asymmetrical figures. Mathematically, this corresponds to the averaging of all points within the figure. Specifically, the geometric center of gravity of is lines and line focus , of surfaces centroid and bodies volume center of gravitycalled. In simple cases, the center of gravity can be obtained through geometrical considerations or, in general, calculated through integration using mathematical means . The methods of analytical geometry are used to describe the bodies . The center of gravity is a gravitational center .

The geometric center of gravity corresponds to the center of mass of a physical body that is made of homogeneous material, i.e. has the same density everywhere . It can therefore also be determined purely mechanically by balancing . This method can be applied to models when it comes to geographical centers of continents or countries (for example center of Europe or center of Germany ).

Geometric center of gravity of finitely many points in real vector space

Are in a - vector space for a natural number pairwise distinct points given, the geometric center of gravity is defined as ${\displaystyle \mathbb {R} }$ ${\displaystyle {\mathcal {V}}}$ ${\displaystyle m}$ ${\displaystyle x_{1},\dots ,x_{m}\in {\mathcal {V}}}$ ${\displaystyle s}$

${\displaystyle s={\frac {1}{m}}{\sum _{i=1}^{m}{x_{i}}}}$  .

The concept of the center ${\displaystyle k}$ of gravity of a - dimensional simplex falls into this context . If such a simplex has the corner points , its center of gravity is nothing more than the geometric center of gravity of its corner points, i.e.: ${\displaystyle \Delta \subset \mathbb {R} ^{n}\;(k,n\in \mathbb {N} _{0})}$ ${\displaystyle v_{0},\ldots ,v_{k}\in \mathbb {R} ^{n}}$ ${\displaystyle s_{\Delta }}$

${\displaystyle s_{\Delta }={\frac {1}{k+1}}{\sum _{i=0}^{k}{v_{i}}}}$  .

The center of gravity of such a simplex is characterized by the fact that its barycentric coordinates are all the same in relation to the simplex, namely

${\displaystyle ={\frac {1}{k+1}}}$

are.

If these finitely many different points form the set of all corner points of a geometric figure in Euclidean space , then the geometric center of gravity of all of these is also called the corner center of gravity of the figure. Examples of this are in particular the segment , the triangle and the tetrahedron . For quadrilaterals , according to Pierre de Varignon (1654–1722), the center of gravity of the corner of a quadrilateral is at the same time the center of the two center lines , i.e. the two connecting lines of opposite side centers.

Focal points of elementary geometric figures

In the following, some focal points of elementary geometric lines, surfaces and bodies are specified and partly justified by geometric considerations.

For axially symmetrical or rotationally symmetrical figures , the specification of the center of gravity is simplified in that it always lies on the axis of symmetry. In the case of figures with several axes of symmetry or point-symmetrical objects, such as, for example, a square or a circle, the focus is at the point of intersection of the axes of symmetry ( center point ) of the figure.

Lines

route

The geometric center of gravity of a line is in its center, i.e. it is identical to its center point .

Circular arc

Center of gravity of an arc

If the section of the circle is rotated and shifted in such a way that the y-axis of the Cartesian coordinate system is an axis of symmetry of the circular arc and the center of the circle lies in the coordinate origin (see picture), then the center of gravity can be passed through

${\displaystyle x_{s}=0\quad y_{s}={\frac {2r^{2}\sin \alpha }{b}}=r{\frac {l}{b}}}$

to calculate. Here is the radius of the circle, the length of the circular arc and the chord length of the circular arc. ${\displaystyle r}$ ${\displaystyle b}$ ${\displaystyle l}$

${\displaystyle 0<\alpha \leq \pi }$

For the formula fails. With the center of gravity can also be calculated for very small angles. ${\displaystyle \alpha =0}$ ${\displaystyle \lim _{\alpha \to 0}{\tfrac {l}{b}}=\cos \alpha }$

If the circle had to be shifted or rotated at the beginning, then the calculated center of gravity must be shifted back or rotated accordingly to complete the calculation.

Flat arch

In order to approximately calculate the center of gravity of a flat arc, it must be shifted in the Cartesian coordinate system so that the center of the line connecting the two end points lies in the origin of the coordinates. Then the center of gravity is slightly below for a good approximation ${\displaystyle h<r}$

${\displaystyle z_{s}\approx {\frac {2h}{3}}}$.

At (semicircle) the center of gravity is exactly . The percentage deviation increases roughly proportionally with h and is approximately 4.7%. This is followed by the expression that indicates the center of gravity in the range of with an accuracy of better than 5 per thousand. The exact position of the center of gravity of the line in the entire area of can be found by inserting into the formula for the center of gravity related to the center of the circle (see section arc above): ${\displaystyle h=r}$ ${\displaystyle {\frac {2r}{\pi }}}$ ${\displaystyle h=r}$ ${\displaystyle {\frac {2000h}{3(1000+47h/r)}}}$ ${\displaystyle (0\leq h\leq r)}$ ${\displaystyle z_{s}(h)}$ ${\displaystyle (0<h\leq 2r)}$ ${\displaystyle \alpha =\arccos(1-h/r)}$ ${\displaystyle r\sin(\alpha )/\alpha }$

${\displaystyle z_{s}=h-r+{\frac {\sqrt {h(2r-h)}}{\arccos(1-h/r)}}}$.

Interestingly, a maximum shows slightly larger than at . If a shift or rotation was necessary at the beginning, the center of gravity must be shifted back accordingly. ${\displaystyle z_{s}}$ ${\displaystyle r}$ ${\displaystyle h\approx 1{,}9r}$

Flat surfaces

In the case of flat surfaces, the center of gravity can generally be determined by suspending the cut-out surface at a point and drawing the perpendicular , a so-called center of gravity . The point of intersection of two gravity lines is the center of gravity. All other gravity lines also intersect in this focus.
In the case of polygons (especially triangles and squares), a distinction is made between three different focal points, depending on the nature of the flat surface:

Area center of gravity, edge center of gravity and corner center of gravity

However, the last two priorities mentioned have hardly any practical application and are therefore more or less of only academic interest.
A homogeneous surface of any, but constant thickness has (to be precise) a center of gravity ; however, one is usually content with the term focus .
In the case of a polygon that only consists of its borders (e.g. from individual thin rods or in the form of a suitably bent wire), its center of gravity is an edge center of gravity.
In a (fictitious) model, in which the mass of the body (the polygon) is only concentrated in the corners (e.g. in the form of spheres of equal weight), one speaks of a corner center of gravity .
The position of these three focal points is the same for polygons with the same external shape, but the above. different nature, usually different from each other; their determination depends on the individual case.

triangle

Center of gravity S of a triangle
${\displaystyle ({\overline {AS}}):({\overline {SD}})=2:1}$
${\displaystyle F_{ABC}:F_{ABS}=({\overline {CE}}):({\overline {SG}})=3:1}$
${\displaystyle F_{ABS}=F_{BCS}=F_{ASC}}$

The bisectors of a triangle are the lines of gravity of the triangle. Its center of gravity (more precisely: area center of gravity ) lies at the common intersection of the three bisectors and . It divides this in a ratio of 2: 1, with the longer of the two sections being the distance from the center of gravity to the corner point. ${\displaystyle S_{a},S_{b}}$ ${\displaystyle S_{c}}$

If the Cartesian coordinates of the corner points of the triangle are known, the center of gravity results as the arithmetic mean . ${\displaystyle S=(x_{s},y_{s})}$

${\displaystyle x_{s}={\frac {1}{3}}(x_{A}+x_{B}+x_{C}),\quad y_{s}={\frac {1}{3}}(y_{A}+y_{B}+y_{C})}$

Its barycentric coordinates are therefore . ${\displaystyle ({\tfrac {1}{3}},{\tfrac {1}{3}},{\tfrac {1}{3}})}$

Expressed by trilinear coordinates of the center of gravity is a triangle with sides , , ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

${\displaystyle \left({\frac {1}{a}},{\frac {1}{b}},{\frac {1}{c}}\right)=(bc,ca,ab)\,.}$

You can also use the length of one side and the height above the same side, e.g. B. with and , determine in Cartesian coordinates. The origin of the coordinate system is in the corner (see illustration). In this way, the Cartesian coordinates of the center of gravity can be passed through ${\displaystyle c}$ ${\displaystyle h_{c}}$ ${\displaystyle A}$

${\displaystyle x_{s}={\frac {c+\xi }{3}},\quad y_{s}={\frac {h_{c}}{3}}}$

to calculate.

The center of gravity of a triangle is the center of the Steiner ellipse (Steiner umellipse) and the Steiner inellipse .

The center of gravity of a triangle is also that clearly defined point in the interior of the triangle, the three connecting lines of which to the corner points of the triangle divide the triangle into three partial triangles with the same area .
The center of gravity of the edge of a triangle (or also: the center of gravity of the circumference of the triangle ) can be determined geometrically in a simple manner - it is its Spieker point .

Trapezoid

Center of gravity of a trapezoid

The center of gravity of the trapezoid can be constructed as follows: A gravity line bisects the two parallel sides. A second is obtained by extending the parallel sides by the length of the other in opposite directions, and connecting the two end points. The formula in Cartesian coordinates is (measured from the lower left corner):

${\displaystyle {\begin{aligned}x_{s}&={\frac {a^{2}-b^{2}+\xi (a+2b)}{3(a+b)}}\\y_{s}&={\frac {h}{3}}\cdot {\frac {a+2b}{a+b}}\end{aligned}}}$

Polygon

Center of gravity in the regular polygon with two lines of gravity and ${\displaystyle S_{1}}$ ${\displaystyle S_{2}}$

The center of gravity of a non-overturned, closed, also irregular polygon with N corner points can be calculated as follows from the Cartesian coordinates of the corner points (the zeroth corner point and the -th corner point are identical here). The corner points are numbered consecutively counterclockwise. The center of gravity of a regular polygon corresponds to the center of its circumference . ${\displaystyle (x_{i},y_{i})}$ ${\displaystyle (x_{0},y_{0})}$ ${\displaystyle N}$ ${\displaystyle (x_{N},y_{N})}$

The area of the polygon can be calculated using the Gaussian triangle formula ${\displaystyle A}$

${\displaystyle A={\frac {1}{2}}\sum _{i=0}^{N-1}(x_{i}\ y_{i+1}-x_{i+1}\ y_{i})}$

to be determined. The centroid of the polygon is then given with the formulas ${\displaystyle S}$

${\displaystyle {\begin{aligned}x_{s}&={\frac {1}{6A}}\sum _{i=0}^{N-1}(x_{i}+x_{i+1})(x_{i}\ y_{i+1}-x_{i+1}\ y_{i})\\y_{s}&={\frac {1}{6A}}\sum _{i=0}^{N-1}(y_{i}+y_{i+1})(x_{i}\ y_{i+1}-x_{i+1}\ y_{i})\end{aligned}}}$

certainly.

Section of a circle

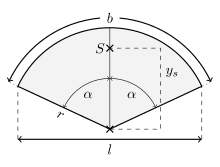
Focus of a part of a circle

If the section of the circle is rotated and shifted so that the y-axis of the Cartesian coordinate system is an axis of symmetry of the section and the center point (of the full circle) is at the origin (see picture), then the center of gravity can be passed through in radians

${\displaystyle y_{s}={\frac {2r\sin \alpha }{3\alpha }}={\frac {2rl}{3b}}}$

with calculate. ${\displaystyle 0<\alpha \leq \pi }$

If the circle had to be shifted or rotated at the beginning, then the calculated center of gravity must be shifted back or rotated accordingly to complete the calculation.

Circle segment

In order to approximately calculate the centroid of a section of a circle, it must be shifted in the Cartesian coordinate system so that the center point of the connecting line between the two end points lies at the origin of the coordinates. Then the center of gravity is slightly above for a good approximation ${\displaystyle h<r}$

${\displaystyle z_{s}\approx {\frac {2h}{5}}}$.

At (semicircle) the center of gravity is exactly . The percentage deviation increases roughly proportionally with h and is approximately 5.8%. This is followed by the expression that indicates the center of gravity in the range of with an accuracy of better than 5 per thousand. The exact position of the center of gravity in the entire area of can be found by inserting into the formula for the center of gravity related to the center of the circle  : ${\displaystyle h=r}$ ${\displaystyle {\frac {4r}{3\pi }}}$ ${\displaystyle h=r}$ ${\displaystyle {\frac {200h}{500-29h/r}}}$ ${\displaystyle (0\leq h\leq r)}$ ${\displaystyle z_{s}(h)}$ ${\displaystyle (0<h\leq 2r)}$ ${\displaystyle \alpha =\arccos(1-h/r)}$ ${\displaystyle 4r\sin(\alpha )^{3}/(6\alpha -3\sin(2\alpha ))}$

${\displaystyle z_{s}=h-r+{\frac {2\left({\sqrt {h(2r-h)}}\right)^{3}}{3\left((h-r){\sqrt {h(2r-h)}}+r^{2}\arccos(1-h/r)\right)}}}$.

If a shift or rotation was necessary at the beginning, the center of gravity must be shifted back accordingly.

body

For three-dimensional bodies , you can calculate both the volume center of gravity, i.e. the center of gravity of the solid body, and the area center of gravity, i.e. the center of gravity of the area that delimits the body.

Pyramid and cone

Center of gravity of a pyramid

In order to calculate the center of gravity of the volume and the center of area of ​​a pyramid or a cone , it is shifted in the oblique coordinate system so that the center of gravity of the base is in the origin of the coordinates and the y-axis goes through the apex. Then the center of gravity of a pyramid or a cone can go through ${\displaystyle (0,0,0)}$

${\displaystyle x_{s}=0,\qquad y_{s}={\frac {h}{4}},\qquad z_{s}=0}$

and the center of gravity of the lateral surface through

${\displaystyle x_{s}=0,\qquad y_{s}={\frac {h}{3}},\qquad z_{s}=0}$

be calculated.

Paraboloid of revolution

Center of gravity of a paraboloid of revolution

In order to calculate the center of gravity of the volume and the center of area of ​​a paraboloid of revolution, it is shifted in the Cartesian coordinate system so that the center of gravity of the base area lies in the coordinate origin . Then you can go through the center of gravity of the volume of the paraboloid of revolution ${\displaystyle (0,0,0)}$

${\displaystyle x_{s}=0,\qquad y_{s}={\frac {h}{3}},\qquad z_{s}=0}$

to calculate. The centroid looks a little more complicated. For the components and also applies again ${\displaystyle x_{s}}$ ${\displaystyle z_{s}}$

${\displaystyle x_{s}=z_{s}=0}$

and the component is included ${\displaystyle y_{s}}$

${\displaystyle y_{s}=h-{\frac {4\pi {\sqrt {f}}\int _{0}^{h}y{\sqrt {f+y}}\,\mathrm {d} y}{4\pi {\sqrt {f}}\int _{0}^{h}{\sqrt {f+y}}\,\mathrm {d} y}}=h\left(1+{\frac {2}{5}}(f/h)-{\frac {3/5}{1-1/(1+h/f)^{3/2}}}\right),}$

where the expression in the denominator of the first fraction represents the surface area of the parabola open to the right with the focal length f. Ab strives against , otherwise against . ${\displaystyle y=2{\sqrt {fx}}}$ ${\displaystyle (f/h)\gtrsim 3}$ ${\displaystyle y_{s}}$ ${\displaystyle {\tfrac {1}{2}}h}$ ${\displaystyle {\tfrac {2}{5}}h}$

Spherical segment

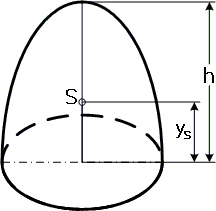
Center of gravity of a spherical segment

To calculate the center of gravity of the volume and the centroid of a spherical segment , the segment is shifted in the Cartesian coordinate system so that the center of the solid sphere lies in the origin of the coordinates . The center of gravity is then through ${\displaystyle (0,0,0)}$

${\displaystyle x_{s}=0,\quad y_{s}={\frac {3(2r-h)^{2}}{4(3r-h)}},\quad z_{s}=0}$

and the center of gravity through

${\displaystyle x_{s}=0,\quad y_{s}=r-{\frac {h}{2}},\quad z_{s}=0}$

calculated. ( ) ${\displaystyle 0\leq h\leq 2\,r}$

Summarize key areas

It is possible to combine several focal points of individual figures into a common focal point of the overall figure, so that the focal point of a composite figure results from the focal points of individual simple elements.

one-dimensional	two-dimensional	three dimensional	general
${\displaystyle x_{s}={\frac {\sum \limits _{i}(x_{s,i}\cdot l_{i})}{\sum \limits _{i}l_{i}}}}$	${\displaystyle x_{s}={\frac {\sum \limits _{i}(x_{s,i}\cdot A_{i})}{\sum \limits _{i}A_{i}}}}$ ${\displaystyle y_{s}={\frac {\sum \limits _{i}(y_{s,i}\cdot A_{i})}{\sum \limits _{i}A_{i}}}}$	${\displaystyle x_{s}={\frac {\sum \limits _{i}(x_{s,i}\cdot V_{i})}{\sum \limits _{i}V_{i}}}}$ ${\displaystyle y_{s}={\frac {\sum \limits _{i}(y_{s,i}\cdot V_{i})}{\sum \limits _{i}V_{i}}}}$ ${\displaystyle z_{s}={\frac {\sum \limits _{i}(z_{s,i}\cdot V_{i})}{\sum \limits _{i}V_{i}}}}$	${\displaystyle {\vec {r}}_{s}={\frac {\sum \limits _{i}({\vec {r}}_{s,i}\cdot V_{i})}{\sum \limits _{i}V_{i}}}}$

The coordinates , and are to be specified in a freely selectable but uniform Cartesian coordinate system. If a surface (a body) has recesses, the sum formulas above can also be used, taking into account that the recessed surfaces (volumes) are included in the calculation with a negative sign . The components of the center of gravity form the vector . ${\displaystyle x_{s}}$ ${\displaystyle y_{s}}$ ${\displaystyle z_{s}}$ ${\displaystyle x_{s},\,y_{s},\,z_{s}}$ ${\displaystyle {\vec {r}}_{s}}$

Definition of the center of gravity by integrals

The formulas for calculating the center of gravity of elementary geometrical figures can be derived using the integrals given below. In the case of more complicated figures, these integrals can often only be determined numerically .

The definition corresponds mathematically to the averaging of all points of the geometric object (body) in Euclidean space . In the case of lines and areas in two-dimensional space , only the coordinates and are to be calculated, the coordinate is not applicable. The integration area is one-dimensional for lines, two-dimensional for surfaces and three-dimensional for bodies. ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle x_{S}}$ ${\displaystyle y_{S}}$ ${\displaystyle z}$

line

For a line of length , the center of gravity is given by ${\displaystyle C}$ ${\displaystyle L}$ ${\displaystyle {\vec {r}}_{S}=(x_{S},y_{S},z_{S})}$

${\displaystyle x_{S}={\frac {1}{L}}\int _{C}x\,\mathrm {d} s,\quad y_{S}={\frac {1}{L}}\int _{C}y\,\mathrm {d} s,\quad z_{S}={\frac {1}{L}}\int _{C}z\,\mathrm {d} s}$

With

${\displaystyle \quad L=\int _{C}\,\mathrm {d} s.}$

These integrals are curve integrals of the first kind .

Surfaces

For an area with area , the center of gravity is defined by ${\displaystyle F}$ ${\displaystyle A}$

${\displaystyle x_{S}={\frac {1}{A}}\int _{F}x\,\mathrm {d} A,\quad y_{S}={\frac {1}{A}}\int _{F}y\,\mathrm {d} A,\quad z_{S}={\frac {1}{A}}\int _{F}z\,\mathrm {d} A}$

With

${\displaystyle \quad A=\int _{F}\mathrm {d} A.}$

These integrals are surface integrals with a scalar surface element.

body

In the case of a restricted body in three-dimensional space with volume , the center of gravity is defined by ${\displaystyle K}$ ${\displaystyle V}$

${\displaystyle x_{S}={\frac {1}{V}}\int _{K}x\,\mathrm {d} V,\quad y_{S}={\frac {1}{V}}\int _{K}y\,\mathrm {d} V,\quad z_{S}={\frac {1}{V}}\int _{K}z\,\mathrm {d} V}$

With

${\displaystyle \quad V=\int _{K}\mathrm {d} V.}$

These integrals are volume integrals .

General

Be a body with volume . The focus of is defined by ${\displaystyle K\subset \mathbb {R} ^{n}}$ ${\displaystyle V}$ ${\displaystyle x_{S}=(x_{s,1},\ldots ,x_{s,n})\in \mathbb {R} ^{n}}$ ${\displaystyle K}$

${\displaystyle x_{s,i}={\frac {1}{V}}\int _{K}x_{i}\,\mathrm {d} V\ \quad {\text{mit}}\quad V=\int _{K}\mathrm {d} V,}$

where is the m-dimensional volume element and the dimension of , is with . ${\displaystyle \mathrm {d} V}$ ${\displaystyle m}$ ${\displaystyle K}$ ${\displaystyle m\leq n}$

Integration with symmetrical objects

In the case of objects, the symmetry elements, e.g. B. have an axis of symmetry or a plane of symmetry , the calculation of the center of gravity is simplified in many cases, since the center of gravity is always contained in the symmetry element. If the object has an axis of symmetry, the volume element can be expressed as a function of the infinitesimal axis element. It only needs to be integrated via the symmetry axis.

Alternative integral formula for areas in ${\displaystyle \mathbb {R} ^{2}}$

Another possibility to calculate the coordinates of the center of gravity of an area results from the formulas:

${\displaystyle x_{s}={\frac {\int _{a}^{b}(x(f(x)-g(x)))\,\mathrm {d} x}{\int _{a}^{b}(f(x)-g(x))\,\mathrm {d} x}}}$, ${\displaystyle y_{s}={\frac {\int _{a}^{b}((f(x))^{2}-(g(x))^{2})\,\mathrm {d} x}{\int _{a}^{b}(2(f(x)-g(x)))\,\mathrm {d} x}},}$

where the limits and intersections of the functions and represent. This formula can be used to calculate the center of gravity of any flat surface that is enclosed between two functions. Conditions for this are , ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle f(x)}$ ${\displaystyle g(x)}$ ${\displaystyle a<x<b}$ ${\displaystyle g(x)<y<f(x).}$

Examples of integral calculus

Line center of gravity of an arc

Center of gravity of an arc

The easiest way to specify points on a flat arc is in polar coordinates . If the y-axis lies on the symmetry line with the origin in the center of the circle, the coordinates are:

${\displaystyle x=r\sin \varphi ,\,y=r\cos \varphi .}$

The length of the arc results from: ${\displaystyle b}$

${\displaystyle b=\int _{K}\mathrm {d} s=\int _{-\alpha }^{\alpha }r\mathrm {d} \varphi =2r\alpha ,}$

where the infinitesimal length element can be substituted by. ${\displaystyle \mathrm {d} s}$ ${\displaystyle r\mathrm {d} \varphi }$

For reasons of symmetry is . For the y-coordinate of the line centroid results from the definition equation: ${\displaystyle x_{S}=0}$

${\displaystyle y_{S}={\frac {1}{b}}\int _{K}y\,\mathrm {d} s={\frac {1}{b}}\int _{-\alpha }^{\alpha }r^{2}\cos \varphi \,\mathrm {d} \varphi .}$

The integration within the boundaries then results

${\displaystyle y_{S}={\frac {r^{2}}{b}}2\sin \alpha =r{\frac {l}{b}}.}$

Center of gravity of a parabola

Parabola with hatched area under the x-axis; the center of gravity (red point) is (0; −1.6). ${\displaystyle y=x^{2}-4}$

For the practical determination of the x-coordinate of the center of gravity in the two-dimensional case, substitute with what corresponds to an infinitesimal surface strip. Furthermore, this corresponds to the function delimiting the area . ${\displaystyle \mathrm {d} A}$ ${\displaystyle y\cdot \mathrm {d} x}$ ${\displaystyle y}$ ${\displaystyle y(x)}$

For the practical calculation of the y-coordinate in the two-dimensional case, there are basically two approaches:

• Either one forms the inverse function and calculates the integral , whereby the "new" integration limits can now be found on the y-axis, ${\displaystyle x(y)}$ ${\displaystyle \textstyle \int _{A}y\mathrm {d} A=\int _{y}y\cdot x(y)\ \mathrm {d} y}$
• or one takes advantage of the fact that the center of gravity of every infinitesimal strip of surface parallel to the y-axis is. Then a simpler formula is obtained for determining the y-coordinate, with the help of which the formation of the inverse function is saved: ${\displaystyle {\tfrac {y(x)}{2}}}$

We are looking for the center of gravity of the area that is defined by a parabola and the x-axis (see adjacent figure). ${\displaystyle y=x^{2}-4}$

First we determine the content of the area ${\displaystyle A}$

${\displaystyle A=\left|\int \limits _{-2}^{2}(x^{2}-4)\,\mathrm {d} x\right|={\frac {32}{3}}}$

The limits of the integral are the zeros of the function when the area is limited by the x-axis.

The coordinate of the center of gravity results in ${\displaystyle x}$

${\displaystyle x_{s}={\frac {1}{A}}\int \limits _{-2}^{2}\int \limits _{y(x)}^{0}x\,\mathrm {d} y\,\mathrm {d} x=-{\frac {1}{A}}\int \limits _{-2}^{2}x\cdot y(x)\,\mathrm {d} x=-{\frac {1}{A}}\int \limits _{-2}^{2}x\cdot (x^{2}-4)\,\mathrm {d} x=0.}$

The coordinate results in ${\displaystyle y}$

${\displaystyle y_{s}={\frac {1}{A}}\int \limits _{-2}^{2}\int \limits _{y(x)}^{0}y\,\mathrm {d} y\,\mathrm {d} x=-{\frac {1}{2A}}\int \limits _{-2}^{2}y(x)^{2}\,\mathrm {d} x=-{\frac {1}{2A}}\int \limits _{-2}^{2}(x^{4}-8x^{2}+16)\,\mathrm {d} x=-1{,}6.}$

See also

• Commandino's theorem
• Bisector

literature

• Hermann Athens, Jörn Bruhn (ed.): Lexicon of school mathematics and related areas . tape 4 : S to Z. Aulis Verlag, Cologne 1978, ISBN 3-7614-0242-2 , p. 943-944 .
• HSM Coxeter: Immortal Geometry . Translated into German by JJ Burckhardt (=  Science and Culture . Volume 17 ). Birkhäuser Verlag, Basel, Stuttgart 1963 ( MR0692941 ).
• Egbert Harzheim : Introduction to combinatorial topology (=  mathematics. Introductions to the subject matter and results of its sub-areas and related sciences ). Scientific Book Society, Darmstadt 1978, ISBN 3-534-07016-X ( MR0533264 ).
• Jens Levenhagen, Manfred Spata: The determination of area centers. In: Vermessungswesen und Raumordnung Volume 60, 1998, pp. 31–42.
• Harald Scheid (Ed.): DUDEN: Rechnen und Mathematik . 4th, completely revised edition. Bibliographical Institute , Mannheim / Vienna / Zurich 1985, ISBN 3-411-02423-2 .
• Thomas Westermann: Mathematics for Engineers . Springer 2011, ISBN 978-3-642-12759-5 , pp. 336–338, ( excerpt in the Google book search)

Web links

Commons : Centroid  - collection of images, videos and audio files

Wiktionary: focus  - explanations of meanings, word origins, synonyms, translations

• Focus of figures on mathematische-basteleien.de
• Center of Mass on Paul's Online Math Notes - Calculus II, Lamar University
• Derivation of formulas for the focus on the triangle
• Flash animation for the focus construction of the triangle (dwu teaching materials)

Individual evidence

1. ↑ Egbert Harzheim: Introduction to combinatorial topology. 1978, p. 31 ff
2. ^ Hermann Athen, Jörn Bruhn (ed.): Lexicon of school mathematics and adjacent areas . Volume 4: S to Z. 1978, p. 944
3. ↑ Coxeter, op.cit., P. 242
4. ↑ DUDEN: arithmetic and mathematics. 1985, p. 652
5. ^ Alfred Böge, Technical Mechanics . Vieweg + Teubner 2009, p. 84 ( limited preview in Google Book Search)
6. ^ Alfred Böge: Technical Mechanics . Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1355-8 , pp. 77 .
7. ↑ Friedrich Joseph Pythagoras Riecke (Ed.): Mathematische Unterhaltungen. First issue. 1973, p. 76
8. ↑ Riecke's proof (and another proof) can be found in the evidence archive .
9. ↑ Calculating the area and centroid of a polygon ( Memento from September 22, 2009 in the Internet Archive )
10. ^ Lothar Papula: Mathematical formula collection for engineers and scientists . Vieweg, Wiesbaden 2006, ISBN 978-3-8348-0156-2 , pp. 32-38 .
11. ↑ Frank Jablonski: Focus ( Memento from December 11, 2009 in the Internet Archive ), University of Bremen, p. 114 (PDF; 688 kB)
12. ^ Alfred Böge et al .: Handbook of mechanical engineering: Basics and applications of mechanical engineering . Springer 2013, page C14, Gl. (39)
13. ↑ p. 34
14. ↑ p. 38
15. ↑ centroid . In: M. Hazewinkel: Encyclopedia of Mathematics . ("Center of a compact set")
16. ^ Norbert Henze , Günter Last: Mathematics for industrial engineers and for scientific-technical courses - Volume II . Vieweg + Teubner, 2004, ISBN 3-528-03191-3 , p. 128 ( excerpt in the Google book search)
17. ↑ David Halliday: Physics / David Halliday; Robert Resnick; Jearl Walker. Edited by the German translator Stephan W. Koch. [The translator Anna Schleitzer…] Wiley-VCH-Verlag, Weinheim 2007, ISBN 978-3-527-40746-0 , p. 192 ( limited preview in Google Book search).
18. ^ Thomas Westermann: Mathematics for Engineers . Springer 2011, ISBN 978-3-642-12759-5 , p. 338 ( excerpt in the Google book search).