Interval arithmetic

In mathematics, interval arithmetic refers to a method for automated error estimation on the basis of completed intervals . Not exactly known real quantities are considered, but they can be limited by two numbers and . It can be between and or one of the two values. Mathematically speaking, this area corresponds to the interval . A function that depends on such an unsafe one cannot be evaluated accurately. After all, it is not known which numerical value should actually be used within for . Instead, the smallest possible interval is determined, which just contains the possible function values for all . Through targeted assessment of endpoints and gives a new function, which in turn reflects on intervals intervals. ${\displaystyle x}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle x}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle [a,b]}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle [a,b]}$ ${\displaystyle x}$ ${\displaystyle [c,d]}$ ${\displaystyle f(x)}$ ${\displaystyle x\in [a,b]}$ ${\displaystyle c}$ ${\displaystyle d}$

This concept is suitable, among other things, for handling rounding errors directly during the calculation and if there are uncertainties in knowing the exact values ​​of physical and technical parameters . The latter often result from measurement errors and component - tolerances . In addition, interval arithmetic can help to obtain reliable solutions to equations and optimization problems .

Body mass index for a 1.80 m tall person in relation to body weight m (in kilograms)

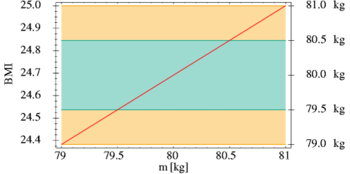
As an example, the calculation of the intended body mass index (BMI of English. Body Mass Index ) are considered. The BMI is the body mass in kilograms divided by the square of the height in meters. As an illustration, the weight determination (actually mass determination) should be done with the help of a bathroom scale, with which the weight can be read off to the nearest kilogram. Intermediate values ​​are never determined - around 79.6 kg or 80.3 kg - but figures rounded to whole numbers. It is of course very unlikely that you really weigh exactly 80.0 kg when this is displayed. With the usual rounding to the nearest weight value, the scale delivers 80 kg for any weight between 79.5 kg and 80.5 kg. The corresponding range of all real numbers that are greater than or equal to 79.5 and at the same time less than or equal to 80.5 can simply be written down as an interval . To avoid confusion, a point is usually used instead of a comma as a decimal separator . ${\displaystyle [79.5,80.5]}$

For a person who weighs 80 kg and is 1.80 m tall, the BMI is approximately 24.7. With a weight of 79.5 kg and the same height, only a value of 24.5 would have to be assumed, whereas 80.5 kg corresponds to almost 24.9. The actual BMI is therefore in the range . In this case, the error can still be neglected in practice, but this is not the case with all invoices. For example, the weight fluctuates over the course of a day, so that the BMI can vary between 24 (still normal weight) and 25 (already overweight). Without a detailed calculation, however, statements cannot always be made from the outset as to whether an error is ultimately big enough to have a significant impact. ${\displaystyle [24.5,24.9]}$

In interval arithmetic, the range of possible results is explicitly calculated. Put simply, one no longer calculates with numbers, but with intervals that do not represent exactly known values. Similar to an error bar around a measured value, an interval expresses the extent of the uncertainty with regard to the variable to be calculated. For this purpose, simple arithmetic operations, such as the basic arithmetic operations or trigonometric functions , are redefined for calculating with intervals in order to obtain the outer limits of a desired value range .

Function subject to tolerance (turquoise) and interval approximation (red)

introduction

The main focus of interval arithmetic is to determine the upper and lower bounds for the value range of a function in one or more variables in the simplest possible way . These limits do not necessarily have to correspond to the supremum or infimum , since the exact calculation of these values ​​is often too difficult. (It can be shown that this task is NP-difficult in general .)

Usually one restricts oneself to the treatment of closed , real intervals, i.e. sets of the form

${\displaystyle [a,b]=\{x\in \mathbb {R} \,|\,a\leq x\leq b\}}$,

where and are also permitted. And correspond to the usually half-open written intervals, which include all real numbers less than or equal to or greater than or equal to . Correspondingly, the interval denotes the entire real axis. ${\displaystyle a={-\infty }}$ ${\displaystyle b={\infty }}$ ${\displaystyle [{-\infty },b]}$ ${\displaystyle [a,{\infty }]}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle [{-\infty },{\infty }]}$

As with classic arithmetic with numbers, it must first be defined how the arithmetic operations and elementary functions are to be applied to intervals. More complex functions can then be put together from these basic elements ( Lit .: Kulisch, 1989).

Basic arithmetic

Body mass index for various weights in relation to body size L (in meters)

The example from the beginning is used again for explanation. When determining the body mass index, body size also plays a role in addition to weight. This is usually only measured in whole centimeters: an indication of the height of 1.80 meters actually means a height somewhere between 1.795 m and 1.805 m. This inaccuracy must be taken into account in addition to the fluctuation range for weight, which is between 79.5 kg and 80.5 kg. For the BMI , as I said, the body mass in kilograms must be divided by the square of the body height in meters. For 79.5 kg and 1.795 m as well as for 80.5 kg and 1.805 m, this results in approximately 24.7. It must now be taken into account, however, that the person in question may only be 1.795 m tall with a weight of 80.5 kg - or 1.805 m with 79.5 kg. The combinations of all possible intermediate values ​​must also be considered. With the help of the interval arithmetic defined below, the interval-valued BMI

${\displaystyle [79{,}5;80{,}5]/([1{,}795;1{,}805])^{2}=[24{,}4;25{,}0]\,}$

can actually be calculated.

An operation between two intervals, where for example stands for addition or multiplication, must meet the condition ${\displaystyle {\langle \!\mathrm {op} \!\rangle }}$ ${\displaystyle {\langle \!\mathrm {op} \!\rangle }}$

${\displaystyle [x_{1},x_{2}]{\,\langle \!\mathrm {op} \!\rangle \,}[y_{1},y_{2}]=\{x{\,\langle \!\mathrm {op} \!\rangle \,}y\,|\,x\in [x_{1},x_{2}]\,{\mbox{und}}\,y\in [y_{1},y_{2}]\}}$

fulfill. This results in the four basic arithmetic operations

${\displaystyle {\begin{matrix}[x_{1},x_{2}]{\,\langle \!\mathrm {op} \!\rangle \,}[y_{1},y_{2}]&=&{\left[\min(x_{1}{\langle \!\mathrm {op} \!\rangle }y_{1},x_{1}{\langle \!\mathrm {op} \!\rangle }y_{2},x_{2}{\langle \!\mathrm {op} \!\rangle }y_{1},x_{2}{\langle \!\mathrm {op} \!\rangle }y_{2}),\right.}\\&&{\left.\;\max(x_{1}{\langle \!\mathrm {op} \!\rangle }y_{1},x_{1}{\langle \!\mathrm {op} \!\rangle }y_{2},x_{2}{\langle \!\mathrm {op} \!\rangle }y_{1},x_{2}{\langle \!\mathrm {op} \!\rangle }y_{2})\right]}\,\mathrm {,} \end{matrix}}}$

if permissible for all and . ${\displaystyle x{\,\langle \!\mathrm {op} \!\rangle \,}y}$ ${\displaystyle x\in [x_{1},x_{2}]}$ ${\displaystyle y\in [y_{1},y_{2}]}$

This can be simplified even further for practical applications:

• Addition : ${\displaystyle [x_{1},x_{2}]+[y_{1},y_{2}]=[x_{1}+y_{1},x_{2}+y_{2}]}$
• Subtraction : ${\displaystyle [x_{1},x_{2}]-[y_{1},y_{2}]=[x_{1}-y_{2},x_{2}-y_{1}]}$
• Multiplication : ${\displaystyle [x_{1},x_{2}]\cdot [y_{1},y_{2}]=[\min(x_{1}y_{1},x_{1}y_{2},x_{2}y_{1},x_{2}y_{2}),\max(x_{1}y_{1},x_{1}y_{2},x_{2}y_{1},x_{2}y_{2})]}$
• Division : where appropriate . ${\displaystyle [x_{1},x_{2}]/[y_{1},y_{2}]=[x_{1},x_{2}]\cdot (1/[y_{1},y_{2}])}$ ${\displaystyle 1/[y_{1},y_{2}]=[1/y_{2},1/y_{1}]}$ ${\displaystyle 0\notin [y_{1},y_{2}]}$

For the division by an interval that contains zero, one first defines

${\displaystyle 1/[y_{1},0]=[-\infty ,1/y_{1}]}$and . ${\displaystyle 1/[0,y_{2}]=[1/y_{2},\infty ]}$

For applies , so that one should actually bet. However, you lose the gap and thus valuable information. Usually one therefore calculates with the subsets and continues individually. ${\displaystyle y_{1}<0<y_{2}}$ ${\displaystyle 1/[y_{1},y_{2}]=[-\infty ,1/y_{1}]\cup [1/y_{2},\infty ]}$ ${\displaystyle 1/[y_{1},y_{2}]=[-\infty ,\infty ]}$ ${\displaystyle (1/y_{1},1/y_{2})}$ ${\displaystyle [-\infty ,1/y_{1}]}$ ${\displaystyle [1/y_{2},\infty ]}$

Because several such splits can occur within an interval calculation, it is sometimes useful to systematize the calculation with so-called multi-intervals of the form . The corresponding multi-interval arithmetic then maintains a disjoint set of intervals and then also ensures, for example, that overlapping intervals are combined ( Lit .: Dreyer, 2005). ${\displaystyle \textstyle \bigcup _{i=1}^{l}[x_{i1},x_{i2}]}$

Since a number can be interpreted as the interval , one immediately receives a rule for combining interval and real-valued quantities. ${\displaystyle r\in \mathbb {R} }$ ${\displaystyle [r,r]}$

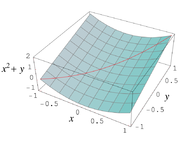
With the help of these definitions, the value range of simple functions such as can be determined. For example , if you put , and , you get ${\displaystyle f(a,b,x)=a\cdot x+b}$ ${\displaystyle a=[1,2]}$ ${\displaystyle b=[5,7]}$ ${\displaystyle x=[2,3]}$

${\displaystyle f(a,b,x)=([1,2]\cdot [2,3])+[5,7]=[1\cdot 2,2\cdot 3]+[5,7]=[7,13]}$.

If one interprets as a function of a variable with interval-valued parameters and , then the set of all zeros of this family of functions can easily be determined. It then applies ${\displaystyle f(a,b,x)}$ ${\displaystyle x}$ ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle f([1,2],[5,7],x)=([1,2]\cdot x)+[5,7]=0\Leftrightarrow [1,2]\cdot x=[-7,-5]\Leftrightarrow x=[-7,-5]/[1,2]}$,

the possible zeros are therefore in the interval . ${\displaystyle [-7,{-2.5}]}$

Multiplication of positive intervals

As in the example above, the multiplication of intervals can often be traced back to the multiplication of just two numbers. It is true

${\displaystyle [x_{1},x_{2}]\cdot [y_{1},y_{2}]=[x_{1}\cdot y_{1},x_{2}\cdot y_{2}]}$if . ${\displaystyle x_{1},y_{1}\geq 0}$

The multiplication can be interpreted here as determining the area of ​​a rectangle with varying edge lengths. The interval result then covers all values ​​from the smallest to the largest possible area.

The same applies if one of the two intervals lies entirely in the non-positive and the other entirely in the non-negative area of ​​the real axis. In general, when multiplying, it must be noted that the result must be set to immediately if there are indefinite values, such as . This occurs e.g. B. in a division where the numerator and denominator both contain zero. ${\displaystyle [{-\infty },{\infty }]}$ ${\displaystyle 0\cdot \infty }$

notation

In order to recognize interval values ​​more easily in mathematical formulas , the square brackets for "marking" are misused.

Accordingly, an interval is called and the set of all real intervals is called ${\displaystyle [x]\equiv [x_{1},x_{2}]}$

${\displaystyle [\mathbb {R} ]:={\big \{}\,[x_{1},x_{2}]\,|\,x_{1}\leq x_{2}\,{\mbox{und}}\,x_{1},x_{2}\in \mathbb {R} \cup \{-\infty ,\infty \}{\big \}}}$

abbreviated. For a box or a vector of intervals used in addition bold typeface : . ${\displaystyle {\big (}[x]_{1},\ldots ,[x]_{n}{\big )}\in [\mathbb {R} ]^{n}}$ ${\displaystyle [\mathbf {x} ]}$

With such a compact notation, it should be noted that it is not confused with a so-called improper interval  in which the upper and lower limits match. ${\displaystyle [x]}$ ${\displaystyle [x_{1},x_{1}]}$

Elementary functions

Range of values ​​of a monotonic function

In order to be able to handle functions with interval methods whose terms do not result from the basic arithmetic operations, one must also redefine other elementary functions for intervals. Existing monotony properties are used here.

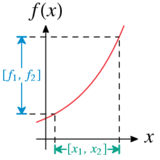
The range of values ​​can also be easily determined for monotonic functions in a variable. If there is a monotonous increase or decrease in an interval , then the inequality applies to all values with ${\displaystyle f:\mathbb {R} \rightarrow \mathbb {R} }$ ${\displaystyle [x_{1},x_{2}]}$ ${\displaystyle y_{1},y_{2}\in [x_{1},x_{2}]}$ ${\displaystyle y_{1}\leq y_{2}}$

${\displaystyle f(y_{1})\leq f(y_{2})}$, or . ${\displaystyle f(y_{1})\geq f(y_{2})}$

The value range of the interval is obtained by evaluating the function at the end points and : ${\displaystyle [y_{1},y_{2}]\subseteq [x_{1},x_{2}]}$ ${\displaystyle y_{1}}$ ${\displaystyle y_{2}}$

${\displaystyle f([y_{1},y_{2}])=\left[\min {\big \{}f(y_{1}),f(y_{2}){\big \}},\max {\big \{}f(y_{1}),f(y_{2}){\big \}}\right]}$.

Therefore, the following intervals of elementary functions can easily be defined:

• Exponential : for , ${\displaystyle a^{[x_{1},x_{2}]}=[a^{x_{1}},a^{x_{2}}]}$ ${\displaystyle a>1}$
• Logarithm : for positive intervals and ${\displaystyle \log _{a}{\big (}{[x_{1},x_{2}]}{\big )}=[\log _{a}{x_{1}},\log _{a}{x_{2}}]}$ ${\displaystyle [x_{1},x_{2}]}$ ${\displaystyle a>1}$
• Odd powers : for odd . ${\displaystyle {[x_{1},x_{2}]}^{n}=[{x_{1}}^{n},{x_{2}}^{n}]}$ ${\displaystyle n\in \mathbb {N} }$

It is also important to be able to determine the range of values ​​for even powers. In contrast to the usual numerics, it does not make sense here to trace the calculation back to the multiplication. For example, moves to within the interval , if . But if you try to determine the form by multiplication , you will get the result in any case . ${\displaystyle x^{n}}$ ${\displaystyle x\in [-1,1]}$ ${\displaystyle [0,1]}$ ${\displaystyle n=2,4,6,\ldots }$ ${\displaystyle [-1,1]^{n}}$ ${\displaystyle [-1,1]\cdot \ldots \cdot [-1,1]}$ ${\displaystyle [-1,1]}$

It makes more sense here to consider the parabola  as a combination of a monotonically decreasing (for ) and a monotonically increasing function (for ). So it is true for even : ${\displaystyle x^{n}}$ ${\displaystyle x<0}$ ${\displaystyle x>0}$ ${\displaystyle n\in \mathbb {N} }$

• ${\displaystyle {[x_{1},x_{2}]}^{n}=[x_{1}^{n},x_{2}^{n}]}$if , ${\displaystyle x_{1}\geq 0}$
• ${\displaystyle {[x_{1},x_{2}]}^{n}=[x_{2}^{n},x_{1}^{n}]}$if , ${\displaystyle x_{2}\leq 0}$
• ${\displaystyle {[x_{1},x_{2}]}^{n}=[0,\max\{x_{1}^{n},x_{2}^{n}\}]}$, otherwise.

More generally, it can be said that for piecewise monotonous functions it is sufficient to calculate them at the end points of  an interval  , as well as at the  so-called critical points contained in . The critical points here correspond to the points at which the monotony properties change. ${\displaystyle x_{1},x_{2}}$ ${\displaystyle [x_{1},x_{2}]}$ ${\displaystyle [x_{1},x_{2}]}$

This can be done e.g. B. apply to sine and cosine , which must also be evaluated in places  or  for all . A maximum of five points play a role here, since the result can be determined immediately  if the input interval contains at least a whole period . In addition, sine and cosine only have to be reevaluated at the edge points, since the corresponding values ​​at the critical points - namely −1, 0, +1 - can be saved in advance. ${\displaystyle \left({}^{1}\!\!/\!{}_{2}+{n}\right)\cdot \pi }$ ${\displaystyle {n}\cdot \pi }$ ${\displaystyle n\in \mathbb {Z} }$ ${\displaystyle [-1,1]}$

Interval extensions for general functions

In general, there is no such simple description of the value range for any function. But you can often extend this to intervals. If is  a function that maps a real-valued vector to a real number, then one calls  an interval extension of  , if holds ${\displaystyle f:\mathbb {R} ^{n}\rightarrow \mathbb {R} }$ ${\displaystyle [f]:[\mathbb {R} ]^{n}\rightarrow [\mathbb {R} ]}$ ${\displaystyle f}$

${\displaystyle [f]([\mathbf {x} ])\supseteq \{f(\mathbf {y} )|\mathbf {y} \in [\mathbf {x} ]\}}$.

This does not clearly define the interval extension. For example, both  and are  admissible extensions of the exponential function. Since expansions that are as sharp as possible are desired, i.e. those that approximate the value range sought as precisely as possible, one will rather choose in this case because it even determines the exact range. ${\displaystyle [f]([x_{1},x_{2}])=[e^{x_{1}},e^{x_{2}}]}$ ${\displaystyle [g]([x_{1},x_{2}])=[{-\infty },{\infty }]}$ ${\displaystyle [f]}$

The natural extension of the interval is obtained by replacing the basic arithmetic operations and elementary functions with their interval-valued equivalents in the function  rule. ${\displaystyle f(x_{1},\cdots ,x_{n})}$

The Taylor interval expansion (of degree ) of a times differentiable function is defined by ${\displaystyle k}$ ${\displaystyle k+1}$ ${\displaystyle f}$

${\displaystyle [f]([\mathbf {x} ]):=}$ ${\displaystyle f(\mathbf {y} )+\sum _{i=1}^{k}{\frac {1}{i!}}\mathrm {D} ^{i}f(\mathbf {y} )\cdot ([\mathbf {x} ]-\mathbf {y} )^{i}+[r]([\mathbf {x} ],[\mathbf {x} ],\mathbf {y} )}$,

for a  , ${\displaystyle \mathbf {y} \in [\mathbf {x} ]}$

where the -th order differential of at the point and an interval extension of the Taylor remainder term ${\displaystyle \mathrm {D} ^{i}f(\mathbf {y} )}$ ${\displaystyle i}$ ${\displaystyle f}$ ${\displaystyle \mathbf {y} }$ ${\displaystyle [r]}$

${\displaystyle r(\mathbf {x} ,\xi ,\mathbf {y} )={\frac {1}{(k+1)!}}\mathrm {D} ^{k+1}f(\xi )\cdot (\mathbf {x} -\mathbf {y} )^{k+1}}$

designated.

Mean value expansion

Since the vector  lies between  and  with , it can also be  estimated by. Usually one chooses for the midpoint of the interval vector and the natural interval extension to estimate the remaining term. ${\displaystyle \xi }$ ${\displaystyle \mathbf {x} }$ ${\displaystyle \mathbf {y} }$ ${\displaystyle \mathbf {x} ,\mathbf {y} \in [\mathbf {x} ]}$ ${\displaystyle \xi }$ ${\displaystyle [\mathbf {x} ]}$ ${\displaystyle \mathbf {y} }$

The special case of the Taylor interval expansion by degree is also known as the mean value interval expansion. For an interval expansion of the Jacobi matrix one obtains here ${\displaystyle k=0}$ ${\displaystyle [J_{f}](\mathbf {[x]} )}$

${\displaystyle [f]([\mathbf {x} ]):=f(\mathbf {y} )+[J_{f}](\mathbf {[x]} )\cdot ([\mathbf {x} ]-\mathbf {y} )}$.

A non-linear function can thus be limited by linear functions.

Interval procedure

The methods of classical numerics cannot be implemented directly for interval arithmetic, since dependencies are usually not taken into account.

Rounded interval arithmetic

Outer rounding for floating point numbers

In order to be able to calculate efficiently with intervals, a concrete implementation must be compatible with calculating with floating point numbers . The operations defined above are based on exact arithmetic, which is not available in fast numerical solving methods. For example, the function's range of values for and would be . If you carry out the same calculation with single-digit precision, the result would usually be too rounded. However , this approach would contradict the basic principles of interval arithmetic, since part of the range of values ​​is lost. Instead, the outwardly rounded solution is preferable. ${\displaystyle f(x,y)=x+y}$ ${\displaystyle x\in [0.1,0.8]}$ ${\displaystyle y\in [0.06,0.08]}$ ${\displaystyle [0.16,0.88]}$ ${\displaystyle [0.2,0.9]}$ ${\displaystyle [0.2,0.9]\not \supseteq [0.16,0.88]}$ ${\displaystyle f([0.1,0.8],[0.06,0.08])}$ ${\displaystyle [0.1,0.9]}$

In addition to standard representations of binary floating point numbers, the IEEE 754 standard also defines precise procedures for carrying out rounding. Accordingly, a system conforming to IEEE 754 must provide the programmer with mathematical rounding (to the next floating point number) and other rounding modes: always rounding up , always rounding down and rounding towards 0 (reduce the result in terms of amount).

The required rounding outwards can therefore be achieved by correspondingly switching the rounding settings of the processor when calculating the upper and lower limits. Alternatively, this can be achieved by adding a suitable narrow interval . ${\displaystyle [\varepsilon _{1},\varepsilon _{2}]}$

Dependency problem and enveloping effect

Overestimation of the range of values

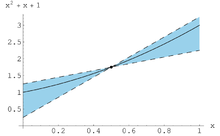
The so-called dependency problem is a major obstacle to using interval arithmetic. Although the range of values ​​of elementary arithmetic operations and functions can be determined very precisely with interval methods, this no longer applies to compound functions. If an interval-valued parameter occurs several times in a calculation, each occurrence is treated independently of one another. This leads to an unwanted inflation of the resulting intervals.

Independent consideration of every occurrence of a variable

For illustration, let us give a function by the expression . The range of values ​​of this function over the interval is actually . In order to obtain the natural extension of the interval, however, one calculates what results in a somewhat larger area. In fact, one actually calculates the infimum and supremum of the function over . It would be better to use an alternative formulation for here that only uses the variable once. In this case, the expression is simply by completing the square to reshape. ${\displaystyle f}$ ${\displaystyle f(x)=x^{2}+x}$ ${\displaystyle [-1,1]}$ ${\displaystyle [-1/4,2]}$ ${\displaystyle [-1,1]^{2}+[-1,1]=[0,1]+[-1,1]=[-1,2]}$ ${\displaystyle h(x,y)=x^{2}+y}$ ${\displaystyle x,y\in [-1,1]}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle f(x)=x^{2}+x}$ ${\displaystyle f(x)=\left(x+{\frac {1}{2}}\right)^{2}-{\frac {1}{4}}}$

Then delivers the corresponding interval calculation

${\displaystyle \left([-1,1]+{\frac {1}{2}}\right)^{2}-{\frac {1}{4}}=\left[-{\frac {1}{2}},{\frac {3}{2}}\right]^{2}-{\frac {1}{4}}=\left[0,{\frac {9}{4}}\right]-{\frac {1}{4}}=\left[-{\frac {1}{4}},2\right]}$

also the correct range of values.

In general, it can be shown that you actually get the exact range of values ​​if each variable appears only once. However, not every function can be resolved appropriately.

Wrapping or "wrapping" effect

The overestimation of the value range caused by the dependency problem can go so far that the result covers such a large range that no meaningful conclusions can be drawn.

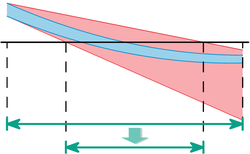
An additional increase in the range of values ​​results from enveloping areas that do not have the form of an interval vector. The solution set of the linear system

${\displaystyle {\begin{matrix}x&=&y\\x&=&p\end{matrix}}}$ For ${\displaystyle p\in [-1,1]}$

is exactly the distance between points and . In the best case, interval methods provide the square that envelops the actual solution ( enveloping or “wrapping” effect ). ${\displaystyle (-1,-1)}$ ${\displaystyle (1,1)}$ ${\displaystyle [-1,1]\times [-1,1]}$

Linear interval systems

A linear interval system consists of an interval-valued matrix and an interval vector . We are then looking for a box that is as narrow as possible that contains all vectors for which there is a pair with and that gives the equation ${\displaystyle [\mathbf {A} ]\in [\mathbb {R} ]^{n\times m}}$ ${\displaystyle [\mathbf {b} ]\in [\mathbb {R} ]^{n}}$ ${\displaystyle [\mathbf {x} ]\in [\mathbb {R} ]^{m}}$ ${\displaystyle \mathbf {x} \in \mathbb {R} ^{m}}$ ${\displaystyle (\mathbf {A} ,\mathbf {b} )}$ ${\displaystyle \mathbf {A} \in [\mathbf {A} ]}$ ${\displaystyle \mathbf {b} \in [\mathbf {b} ]}$

${\displaystyle \mathbf {A} \cdot \mathbf {x} =\mathbf {b} }$

Fulfills.

For quadratic systems - i.e. for - such an interval vector , which contains all possible solutions, can be determined very easily with the interval Gaussian method . To do this, the numerical operations that appear in the Gaussian elimination method known from linear algebra are replaced by their interval versions. However, since the interval-valued entries from and multiple times are included in the calculation while this method is being processed , this approach suffers greatly from the dependency problem. Consequently, the interval Gaussian is only suitable for rough first estimates that contain the entire solution set, but also a very large area outside of it. ${\displaystyle n=m}$ ${\displaystyle [\mathbf {x} ]}$ ${\displaystyle [\mathbf {A} ]}$ ${\displaystyle [\mathbf {b} ]}$

A rough solution can often be improved by intervalising the Gauss-Seidel method . This is motivated as follows: The -th line of the interval-valued linear equation ${\displaystyle [\mathbf {x} ]}$ ${\displaystyle i}$

${\displaystyle {\begin{pmatrix}{[a_{11}]}&\cdots &{[a_{1n}]}\\\vdots &\ddots &\vdots \\{[a_{n1}]}&\cdots &{[a_{nn}]}\end{pmatrix}}\cdot {\begin{pmatrix}{x_{1}}\\\vdots \\{x_{n}}\end{pmatrix}}={\begin{pmatrix}{[b_{1}]}\\\vdots \\{[b_{n}]}\end{pmatrix}}}$

can be resolved for the variable if division is allowed. It therefore applies at the same time ${\displaystyle x_{i}}$ ${\displaystyle 1/[a_{ii}]}$

${\displaystyle x_{j}\in [x_{j}]}$ and . ${\displaystyle x_{j}\in {\frac {[b_{i}]-\sum \limits _{k\not =j}[a_{ik}]\cdot [x_{k}]}{[a_{ij}]}}}$

So you can get through now ${\displaystyle [x_{j}]}$

${\displaystyle [x_{j}]\cap {\frac {[b_{i}]-\sum \limits _{k\not =j}[a_{ik}]\cdot [x_{k}]}{[a_{ij}]}}}$

replace, and thus improve the vector element by element. Since the method is more efficient for diagonally dominant matrices, one often tries instead of the system the matrix equation resulting from multiplication with a suitable real matrix ${\displaystyle [\mathbf {x} ]}$ ${\displaystyle [\mathbf {A} ]\cdot \mathbf {x} =[\mathbf {b} ]{\mbox{,}}}$ ${\displaystyle \mathbf {M} }$

${\displaystyle (\mathbf {M} \cdot [\mathbf {A} ])\cdot \mathbf {x} =\mathbf {M} \cdot [\mathbf {b} ]}$

to solve. For example, if you choose for the midpoint matrix , then is an outer approximation of the identity matrix . ${\displaystyle \mathbf {M} =\mathbf {A} ^{-1}}$ ${\displaystyle \mathbf {A} \in [\mathbf {A} ]}$ ${\displaystyle \mathbf {M} \cdot [\mathbf {A} ]}$

For the methods mentioned above, however, it is true that they only work well if the width of the intervals that occur is sufficiently small. For wider intervals, it can be useful to reduce an interval-linear system to a finite (albeit large) number of real-valued linear systems. If all matrices are invertible, then it is completely sufficient to consider all possible combinations at (upper and lower) end points of the intervals that occur. The resulting sub-problems can then be solved using conventional numerical methods. Interval arithmetic is only used to determine rounding errors. ${\displaystyle \mathbf {A} \in [\mathbf {A} ]}$

However, this approach is only possible for systems of smaller dimensions, since with a fully occupied matrix real matrices have to be inverted, each with vectors for the right side. This approach was continued and improved by Jiří Rohn . ${\displaystyle n\times n}$ ${\displaystyle 2^{n^{2}}}$ ${\displaystyle 2^{n}}$

Interval Newton method

Reduction of the search area in the interval Newton step for "thick" functions

An interval variant of Newton's method for determining the zeros in an interval vector can easily be derived from the mean value expansion ( Lit .: Hansen, 1992). For an unknown vector , a fixed one holds that ${\displaystyle [\mathbf {x} ]}$ ${\displaystyle \mathbf {z} \in [\mathbf {x} ]}$ ${\displaystyle \mathbf {y} \in [\mathbf {x} ]}$

${\displaystyle f(\mathbf {z} )\in f(\mathbf {y} )+[J_{f}](\mathbf {[x]} )\cdot (\mathbf {z} -\mathbf {y} )}$.

For a zero is , and therefore must ${\displaystyle \mathbf {z} }$ ${\displaystyle f(z)=0}$

${\displaystyle f(\mathbf {y} )+[J_{f}](\mathbf {[x]} )\cdot (\mathbf {z} -\mathbf {y} )=0}$.

be fulfilled. So you get . An external estimate of can be determined using one of the linear methods. ${\displaystyle \mathbf {z} \in \mathbf {y} -[J_{f}](\mathbf {[x]} )^{-1}\cdot f(\mathbf {y} )}$ ${\displaystyle [J_{f}](\mathbf {[x]} )^{-1}\cdot f(\mathbf {y} ))}$

In each Newton step a rough start value is now by replacing and so iteratively improved. In contrast to the classic method, this method approaches the zeros from the outside. It is therefore guaranteed that the result always contains all zeros in the start value. Conversely, it has been proven that in has no zero if the Newton step returns the empty set. ${\displaystyle [\mathbf {x} ]\in [\mathbb {R} ]^{n}}$ ${\displaystyle [\mathbf {x} ]\cap \left(\mathbf {y} -[J_{f}](\mathbf {[x]} )^{-1}\cdot f(\mathbf {y} )\right)}$ ${\displaystyle f}$ ${\displaystyle [\mathbf {x} ]}$

The method converges to a set that contains all zeros (within the starting region). The divisions by zero that exist in this case often result in several interval vectors that separate the zeros from one another. This separation is not always complete and can then be forced through bisection .

As an example, consider the function , the start value and the point . Then you have and the first Newton step is given by ${\displaystyle f(x)=x^{2}-2}$ ${\displaystyle [x]=[-2,2]}$ ${\displaystyle y=0}$ ${\displaystyle J_{f}(x)=2\,x}$

${\displaystyle [-2,2]\cap \left(0-{\frac {1}{2\cdot [-2,2]}}(0-2)\right)=[-2,2]\cap {\Big (}[{-\infty },{-0.5}]\cup [{0.5},{\infty }]{\Big )}}$.

So it applies to a zero . Further Newton steps are then applied to and separately. These converge at arbitrarily small intervals around and . ${\displaystyle x\in [{-2},{-0.5}]\cup {\big [}{0.5},{2}{\big ]}}$ ${\displaystyle x\in [{-2},{-0.5}]}$ ${\displaystyle [{0.5},{2}]}$ ${\displaystyle -{\sqrt {2}}}$ ${\displaystyle +{\sqrt {2}}}$

The interval Newton method can easily be used for thick functions , i.e. functions such as those that return intervals when real numbers are used. The solution then consists of several intervals . ${\displaystyle g(x)=x^{2}-[2,3]}$ ${\displaystyle \left[-{\sqrt {3}},-{\sqrt {2}}\right]\cup \left[{\sqrt {2}},{\sqrt {3}}\right]}$

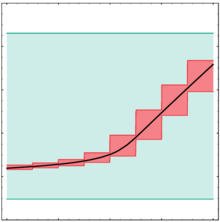
Bisection and overlap

The various interval methods only provide extremely conservative estimates of a particular area being sought, since dependencies between the interval values ​​are not sufficiently taken into account. The dependency problem plays less of a role, however, the thinner the intervals are.

If one covers an interval vector with smaller boxes so that then applies to the value range For the above-mentioned interval extensions then applies . Since there is often a real superset of the right-hand side, this usually gives an improved estimate. ${\displaystyle [\mathbf {x} ]}$ ${\displaystyle [\mathbf {x} _{1}],\cdots ,[\mathbf {x} _{k}]{\mbox{,}}}$ ${\displaystyle \textstyle [\mathbf {x} ]=\bigcup _{i=1}^{k}[\mathbf {x} _{i}]{\mbox{,}}}$ ${\displaystyle \textstyle f([\mathbf {x} ])=\bigcup _{i=1}^{k}f([\mathbf {x} _{i}]){\mbox{.}}}$ ${\displaystyle \textstyle [f]([\mathbf {x} ])\supseteq \bigcup _{i=1}^{k}[f]([\mathbf {x} _{i}])}$ ${\displaystyle [f]([\mathbf {x} ])}$

Overestimation (turquoise) and improved assessment through "Mincing" (red)

Such an overlap can on the one hand be generated by bisection by dividing particularly thick elements of the interval vector, for example in the middle, and replacing them with two intervals and . If the result that follows is still not suitable, it can be further broken down successively. It should be noted, however, that divided vector elements result in an overlap of interval vectors , which of course greatly increases the computational effort. ${\displaystyle [x_{i1},x_{i2}]}$ ${\displaystyle [\mathbf {x} ]=([x_{11},x_{12}],\cdots ,[x_{n1},x_{n2}])}$ ${\displaystyle [x_{i1},(x_{i1}+x_{i2})/2]}$ ${\displaystyle [(x_{i1}+x_{i2})/2,x_{i2}]}$ ${\displaystyle r}$ ${\displaystyle 2^{r}}$

In the case of very wide intervals, it can even make sense to split all intervals into several sub-intervals with a (smaller) constant width (“mincing”). This saves the interim invoice for the individual bisection steps. Both approaches, however, are only suitable for low- dimension problems .

application

The interval arithmetic comes in various fields used to treat quantities for which no exact numerical values can be set ( Ref : Jaulin and others, 2001).

Rounding error analysis

The interval arithmetic is used in the error analysis in order to get control over the rounding errors occurring in every calculation . The advantage of interval arithmetic is that after each operation you get an interval that safely includes the result. The current calculation error can be read directly from the distance between the interval limits:

Error = for the given interval . ${\displaystyle \mathrm {abs} (a-b)}$ ${\displaystyle [a,b]}$

Interval analysis does not offer a replacement for the classic methods of error reduction, such as pivoting , but merely supplements them.

Tolerance analysis

When simulating technical and physical processes, parameters often arise that cannot be assigned exact numerical values. The production process of technical components is subject to certain tolerances, so certain parameters can fluctuate within certain intervals. In addition, many natural constants cannot be measured with any precision ( Lit .: Dreyer, 2005).

If the behavior of such a tolerance-afflicted system is described, for example, by an equation for and unknowns , then the set of all possible solutions ${\displaystyle f(\mathbf {x} ,\mathbf {p} )=0}$ ${\displaystyle \mathbf {p} \in [\mathbf {p} ]}$ ${\displaystyle \mathbf {x} }$

${\displaystyle \{\mathbf {x} \,|\,\exists \mathbf {p} \in [\mathbf {p} ],f(\mathbf {x} ,\mathbf {p} )=0\}}$,

can be estimated by interval methods. These represent an alternative to the classic error calculation . In contrast to point-based methods such as Monte Carlo simulation , the methodology used ensures that no parts of the solution area are overlooked. However, the result always corresponds to a worst case analysis for uniformly distributed errors ; other probability distributions are not possible.

Fuzzy arithmetic

Approximation of the normal distribution by a sequence of intervals

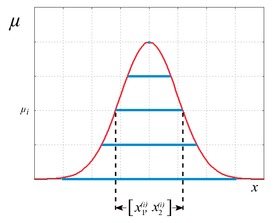
Interval arithmetic can also be used to approximate any membership functions for fuzzy sets such as those used in fuzzy logic . In addition to the strict statements and , intermediate values to which real numbers are assigned are also possible . This corresponds to secure belonging and not belonging . A distribution function assigns a certain fluctuation range to each of these values, which can again be understood as an interval. ${\displaystyle x\in [x]}$ ${\displaystyle x\not \in [x]}$ ${\displaystyle \mu \in [0,1]}$ ${\displaystyle \mu =1}$ ${\displaystyle \mu =0}$

For fuzzy arithmetic , only finitely many discrete membership levels are considered. The shape of such a distribution for a fuzzy value can then be given by a series of intervals ${\displaystyle \mu _{i}\in [0,1]}$

${\displaystyle \left[x^{(1)}\right]\supset \left[x^{(2)}\right]\supset \cdots \supset \left[x^{(k)}\right]}$

be approximated. The interval corresponds exactly to the fluctuation range for the level . ${\displaystyle [x^{(i)}]}$ ${\displaystyle \mu _{i}}$

The corresponding distribution for a function with regard to fuzzy values and the corresponding sequences can then be approximated by the interval sequence . The values are given by and can be estimated using the interval method. The result corresponds to an interval calculation. ${\displaystyle f(x_{1},\cdots ,x_{n})}$ ${\displaystyle x_{1},\cdots ,x_{n}}$ ${\displaystyle \left[x_{1}^{(1)}\right]\supset \cdots \supset \left[x_{1}^{(k)}\right],\cdots ,\left[x_{n}^{(1)}\right]\supset \cdots \supset \left[x_{n}^{(k)}\right]}$ ${\displaystyle \left[y^{(1)}\right]\supset \cdots \supset \left[y^{(k)}\right]}$ ${\displaystyle \left[y^{(i)}\right]}$ ${\displaystyle \left[y^{(i)}\right]=f\left(\left[x_{1}^{(i)}\right],\cdots \left[x_{n}^{(i)}\right]\right)}$ ${\displaystyle \left[y^{(1)}\right]}$

History

Interval arithmetic is not a completely new phenomenon in mathematics and has appeared several times under different names throughout history. Archimedes calculated as early as the 3rd century BC Chr. , Upper and lower bounds for the circuit number Pi . However, calculating with intervals has never been as popular as other numerical techniques, but has never been completely forgotten.

Finally, rules for calculating with intervals and other subsets of real numbers can be found in a 1931 paper by Rosalind Tanner (Rosalind Cecily Young), a doctoral student of Ernest William Hobson at Cambridge University . Work for an arithmetic of range numbers (" range numbers ") with a view to improving and reliability of digital systems can then be found in a textbook on linear algebra by Paul S. Dwyer ( University of Michigan ) published in 1951 . Here, intervals are actually used to estimate the rounding errors in floating point numbers.

The publication of the book Interval Analysis by Ramon E. Moore in 1966 ( Lit .: Moore) is regarded as the hour of birth of modern interval arithmetic . He had the idea for this in the spring of 1958, and just under a year later he published an article on computer-aided interval arithmetic. It is thanks to him that a simple principle has become a generally applicable method for automated error analysis, with the help of which not only the influence of roundings could be determined.

Independently of this, Mieczyslaw Warmus had proposed formulas for calculating with intervals as early as 1956, but Moore found not only implementation instructions but also first non- trivial applications.

In Germany in the 1960s, research groups around Karl Nickel ( University of Karlsruhe ; from 1976: University of Freiburg ), Ulrich Kulisch ( lit .: Kulisch) (University of Karlsruhe) and Fritz Krückeberg ( lit .: Krückeberg) ( University of Bonn ; from 1968 : Society for Mathematics and Data Processing , Sankt Augustin), in which numerous diploma and doctoral theses on interval arithmetic topics were created.

The first international symposium on interval analysis ( Lit .: Hansen) was organized by the Oxford University Computing Laboratory in January 1968 in Culham, England. The conference proceedings were edited by Eldon R. Hansen , who was also later very active in the field ( lit .: Hansen, Walster).

Karl Nickel was the driving force behind five workshops on interval arithmetic, which took place from 1968 to 1976 in the mathematical research institute Oberwolfach and where German-speaking researchers exchanged their work. In 1975, 1980 and 1985 ( Lit .: Nickel) he organized international symposia on interval mathematics, where he coined the term interval mathematics. An interval library, in which software for interval arithmetic was systematically collected, was located in his institute. From 1978 to 1987 he published the journal “Freiburg Interval Reports”. He was the founder and chairman of the GAMM Interval Mathematics Committee.

Two students of Ulrich Kulisch, Götz Alefeld and Jürgen Herzberger, published the first German-language textbook ( lit .: Alefeld and Herzberger) on interval arithmetic in 1974 .

The journal Reliable Computing (originally Interval Computations ) has been published since the 1990s and is dedicated to the reliability of computer-aided calculations. As a senior editor, R. Baker Kearfott contributed significantly to the standardization of the notation and terminology of interval arithmetic in addition to his work on global optimization ( Web : Kearfott).

More recently, the work on estimating the archetype of parameterized functions and on robust control by the COPRIN working group of the INRIA in Sophia Antipolis, France, should be mentioned ( web : INRIA).

Patents

One of the main promoters of interval arithmetic, G. William Walster from Sun Microsystems , filed  several patents in the field of interval arithmetic with the US Patent and Trademark Office in 2003/04 - partly together with Ramon E. Moore and Eldon R. Hansen . The validity of these claims, however, is highly controversial in the interval arithmetic research community, since they may only reflect the prior art .

Implementations

There are many software packages that allow the development of numerical applications using interval arithmetic. These are mostly implemented in the form of program libraries. However, there are C ++ - and Fortran - translator which interval data types possess and according to appropriate operations as a language extension so that interval arithmetic is supported directly.

Since 1967, initially was developed at the University of Karlsruhe XSC extensions for scientific computing ( "E x tensions for S cientific C omputation") for various programming languages, including C ++, Fortran and Pascal. The platform was initially a Zuse Z 23, for which a new interval data type with corresponding elementary operators was made available.

In 1976, Pascal-SC was followed by a Pascal variant on a Zilog Z80 , which made it possible to quickly create complex routines for automated result verification. This was followed by the Fortran 77-based ACRITH-XSC for the System / 370 architecture, which is later also supplied by IBM . From 1991 onwards, Pascal-XSC can be used to generate code for C compilers, and a year later the C ++ class library C-XSC already supports many different computer systems. In 1997, all XSC variants are placed under the General Public License and are thus freely available. At the beginning of the 2000s, C-XSC 2.0 was redesigned under the leadership of the working group for scientific computing at the University of Wuppertal in order to better meet the C ++ standard that has now been adopted.

Another C ++ class library is the profile / BIAS  (“Programmer's Runtime Optimized Fast Interval Library, Basic Interval Arithmetic”) created in 1993 at the Technical University of Hamburg-Harburg , which makes the usual interval operations available in a user-friendly manner. Special emphasis was placed on the efficient use of hardware, portability and independence from a special interval display.

The Boost collection of C ++ libraries also contains a Template class for intervals. Their authors are currently endeavoring to include interval arithmetic in the C ++ language standard.

Today, the common computer algebra systems such as Mathematica , Maple and MuPAD can also handle intervals. There is also the INTLAB extension for Matlab , which is based on BLAS routines, and the b4m toolbox , which provides a profile / BIAS interface.

IEEE Standard 1788-2015

An IEEE standard for interval arithmetic was published in June 2015. There are two free reference implementations that have been developed by members of the working group: the libieeep1788 library for C ++ and the interval package for GNU Octave .

A simplified variant of the standard is still being developed. This should be even easier to implement and ensure faster dissemination.

Conferences and workshops

Several international conferences and workshops are held annually around the world. The most important conference is SCAN (International Symposium on Scientific Computing, Computer Arithmetic, and Verified Numerical Computation). There are also SWIM (Small Workshop on Interval Methods), PPAM (International Conference on Parallel Processing and Applied Mathematics) and REC (International Workshop on Reliable Engineering Computing).

See also

• Automatic differentiation
• Multi-grid method
• Monte Carlo simulation
• Measurement uncertainty
• INTLAB

credentials

literature

• Götz Alefeld, Jürgen Herzberger: Introduction to interval calculation . (= Computer Science, Volume 12). Bibliographisches Institut, BI-Wissenschaftsverlag, Mannheim / Vienna / Zurich 1974, ISBN 3-411-01466-0 .
• H. Bauch, K.-U. Jahn, D. Oelschlägel, H. Süße, V. Wiebigke: Interval Mathematics . BSB Teubner, Leipzig 1987, ISBN 3-322-00384-1 .
• Alexander Dreyer: Interval Analysis of Analog Circuits with Component Tolerances . PhD thesis. Shaker Verlag , Aachen 2003, ISBN 3-8322-4555-3 .
• Eldon R. Hansen (Ed.): Topics in Interval Analysis. Symposium on Interval Analysis, Culham, England, 1968. Clarendon Press, Oxford (1969), ISBN 0-1985-3333-0 .
• Eldon Hansen, G. William Walster: Global Optimization using Interval Analysis. 2. revised Edition. Marcel Dekker, New York 2004, ISBN 0-8247-4059-9 .
• Hanss, Michael: Applied Fuzzy Arithmetic. 2nd Edition. Springer-Verlag, Berlin Heidelberg, 2010, ISBN 978-3-540-27317-2 .
• L. Jaulin, M. Kieffer, O. Didrit, É. Walter: Applied Interval Analysis: With examples in parameter estimation robust control and robotics . Springer, London 2001, ISBN 1-85233-219-0 .
• Fritz Krückeberg: Interval analytical methods in numerical data processing. In: The Minister for Science and Research of the State of North Rhine-Westphalia, State Office for Research, Yearbook 1970, Westdeutscher Verlag Opladen (1971).
• Ulrich Kulisch: Scientific computing with result verification. An introduction. Vieweg-Verlag, Wiesbaden 1989, ISBN 3-528-08943-1 .
• RE Moore: Interval Analysis . Prentice-Hall, Englewood Cliff, NJ 1966, ISBN 0-13-476853-1 .
• Karl Nickel (Ed.): Interval Mathematics: Proceedings of the International Symposium, Karlsruhe, West Germany, May 20-24, 1975. Lecture Notes in Computer Science 29, Springer 1975, ISBN 3-540-07170-9
• Karl Nickel (Ed.): Interval Mathematics 1980, Academic Press, New York, London, Toronto 1980.
• Karl Nickel (Ed.): Interval Mathematics 1985: Proceedings of the International Symposium, Freiburg i. Br., Federal Republic of Germany, September 23-26, 1985. Lecture Notes in Computer Science 212, Springer 1986, ISBN 3-540-16437-5

Web links

• Brian Hayes, 'A Lucid Interval', good introduction (pdf) (83 kB)
• Introductory film (mpeg) ( MPG ; 54.4 MB) by the COPRIN team at INRIA , Sophia Antipolis
• Bibliography by R. Baker Kearfott , University of Louisiana , Lafayette
• Bibliography by Arnold Neumaier , University of Vienna
• Interval calculation in the lexicon of mathematics on Spektrum.de
• kv on GitHub
• arb on GitHub
• JuliaIntervals on GitHub

swell

1. ↑ Publications by Jiří Rohn ( Memento of September 7, 2007 in the Internet Archive )
2. ↑ Hanss, Michael: Applied Fuzzy Arithmetic. 2nd Edition. Springer-Verlag, Berlin Heidelberg, 2010, ISBN 978-3-540-27317-2 , chapter 3.
3. ↑ A Treatise on Early Articles by RE Moore
4. ↑ Early work by M. Warmus ( Memento of the original from April 18, 2008 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.  
5. ↑ Nickel obituary
6. ↑ doctoral students nickel ; Kulisch ; Krückeberg
7. ^ Mathematisches Forschungsinstitut Oberwolfach, Conference Reports Interval Calculation 1968 ; 1969 ; 1972 ; 1973 ; 1976
8. ↑ Patent specifications using interval arithmetic at the US Patent and Trademark Office
9. ↑ Software for interval calculations, compiled by Vladik Kreinovich , University of Texas , El Paso
10. ↑ Example of an interval arithmetic class in C ++ ( Memento of the original from March 30, 2005 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. by Sun Microsystems  
11. ↑ C ++ and Fortran compilers with interval support from Sun Microsystems
12. ^ History of the XSC extensions ( Memento from September 29, 2007 in the Internet Archive )
13. ↑ Proposal for an extension of the C ++ standards to include intervals
14. ↑ INTerval LABoratory and b4m ( Memento from May 1, 2008 in the Internet Archive )
15. ^ IEEE Standard for Interval Arithmetic
16. ^ Revol, Nathalie (2015). The (near-) future IEEE 1788 standard for interval arithmetic. 8th small workshop on interval methods. Set of slides (PDF, English)
17. ↑ IEEE Interval Standard Working Group - P1788
18. ↑ C ++ implementation of the preliminary IEEE P1788 standard for interval arithmetic
19. ↑ GNU Octave interval package
20. ↑ IEEE Project P1788.1