Continuum mechanics

Continuum mechanics is a branch of mechanics that studies the movement of deformable bodies in response to external loads . The term deformation is taken so broadly that it also includes the flow of a liquid or the flow of a gas. Accordingly, solid mechanics , fluid mechanics and gas theory belong to continuum mechanics. In continuum mechanics, the microscopic structure of matter, for example the lattice structure of crystalline solids and the molecular structure of liquids, is disregarded and the object of investigation is approximated as a continuum . The quantities density , temperature and the three components of speed are present at every point in space within a body, which makes continuum mechanics a field theory . The non-classical theories of continuum mechanics include the relativistic continuum mechanics, the Cosserat continuum, in which every material point has three additional degrees of freedom of rotation or the non-local materials.

The theoretical background of continuum mechanics lies in physics , the practical application takes place in different areas of mechanical engineering , theoretical civil engineering , materials science , medical informatics as well as in geophysics and other areas of geosciences. In particular, applications in the first two areas are summarized as technical mechanics .

The numerical calculation method, the finite element method , which is best known and most widely used in the field of scientifically technical tasks in solid mechanics , solves the equations of continuum mechanics (approximately) with methods of the calculus of variations . In fluid mechanics, the finite volume method is of equal importance .

history

The continuum mechanics is based on the mechanics , physics , differential geometry , differential and integral calculus whose historical development can be looked up there. Some stages in the development of fluid mechanics also run parallel to continuum mechanics. At this point the specific continuum mechanical development with emphasis on the mechanics of solid bodies is to be sketched.

Archimedes (287–212 BC) already dealt with fundamental mechanical questions concerning solids and fluids, more than 1500 years before Leonardo da Vinci (1452–1519) came up with solutions to numerous mechanical problems.

Galileo Galilei (1564–1642) discussed strength problems in his Discorsi and thus established strength theory at a time when solid bodies were mostly modeled as undeformable. Edme Mariotte (1620–1684) made contributions to problems of liquids and gases and established the first constitutive laws , which Robert Hooke (1635–1703) also did for elastic solids with Hooke's law named after him in 1676.

Isaac Newton (1643–1727) published his Principia in 1686 with the laws of gravitation and motion. The members of the Bernoulli family made contributions to mathematics, fluid mechanics and - through Jakob I Bernoulli (1654–1705) - to the beam theory . Leonhard Euler (1707–1783) gave important impulses for the mechanics of rigid and deformable bodies as well as for hydromechanics. Jean-Baptiste le Rond d'Alembert (1717–1783) introduced Euler's approach , derived the local mass balance and formulated the d'Alembert principle . Joseph-Louis Lagrange (1736–1813) aligned mechanics consistently mathematically in his fundamental work Mécanique analytique in 1788 .

The fundamental concepts of stress and strain tensor in continuum mechanics were introduced by Augustin-Louis Cauchy (1789–1857). Other fundamental findings were brought in by Siméon Denis Poisson (1781–1840), Claude Louis Marie Henri Navier (1785–1836), Gabrio Piola (1794–1850) and Gustav Robert Kirchhoff (1824–1887).

As a result of industrial and practical needs, technical issues dominated the science that was pursued in France in the École polytechnique, which was shaped by Cauchy, Poisson and Navier . Their model spread throughout Europe, in Germany as a technical university . Engineering disciplines such as plasticity theory , creep theory, strength theory , elasticity theory and civil engineering emerged. As a result of this fragmentation, research and teaching in the sub-areas developed independently of one another and the continuum mechanical relationships were lost. Fluid mechanics also developed independently.

David Hilbert (1862–1943) gave a new impulse to thought with his 1900 list of 23 mathematical problems awaiting solution. The sixth problem, “How can physics be axiomatized?” Is still unsolved at the beginning of the 21st century, but interdisciplinary work on continuum mechanics, especially by Georg Hamel (1877–1954) , arose before the Second World War . After the war, intensive interdisciplinary basic research began, in which Clifford Truesdell (1919–2000) and Walter Noll (1925–2017) provided impetus.

From the middle of the 20th century, computer hardware and software, and numerical methods for solving equations, developed so far that solutions for complex, practical, continuum mechanical problems can be found with their help.

overview

Continuum mechanics contains two different categories of statements:

1. general statements that apply to all material bodies, and
2. individual statements that model material properties.

The general statements describe the kinematics , here the geometry of the deformation of a body, and the laws of nature that determine the physical behavior of matter .

The individual statements about the material properties are made in material theory and create the connection between the laws of nature and the deformations of bodies.

The mathematical description allows the compact formulation of the laws of nature in balance equations and the material properties in constitutive equations. The system off

1. kinematic equations,
2. Balance equations and
3. constitutive equations

is completed and leads to the basic predictability of the reaction of bodies to external influences.

kinematics

In continuum mechanics, the task of kinematics is to define a measure for the distortion of a body depending on its movement - including deformations. The movement can be observed from a fixed point in space or from a particle of the body. The former is Euler's approach , which uses fluid mechanics, and the latter, the Lagrangian , which is preferred in solid mechanics.

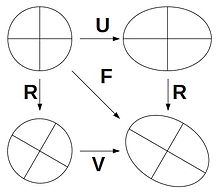
Now it is plausible that if two neighboring particles of a body move very differently in the undeformed initial state, the body there is also strongly deformed. If the positional differences of the particles in the deformed body, measured in three spatial directions, are related to their three positional differences in the undeformed initial state, the deformation gradient arises as the spacing of the particles becomes smaller , which is a local measure of the deformation of the body. The deformation gradient can be broken down into a rotation and a rotation-free stretching , from which the desired degree of distortion can be derived.

Linear mapping of a vector through a tensor T. ${\displaystyle {\vec {v}}}$

The deformation gradient, like the elongation and the distortion measures, is a second order tensor . These tensors are used here for the linear mapping of geometric vectors , which are generally rotated and stretched in the process, see figure on the right. The tensor calculus cannot be assumed to be generally known, which is why every textbook on continuum mechanics also includes an introduction to tensor calculus.

Laws of nature

When the material body is transferred into a mathematical space, the body is homogenized by replacing the matter distributed among atoms with a continuum, which gives this science its name. This idealization gives each point of the body physical properties such as speed, density and temperature.

Newton's second law describes the reaction of a body to an external force . In reality and in continuum mechanics, such forces are always introduced over a large area that are propagated in the body as tensions (with the dimension force per area). Now the body can be mentally cut up so that cutting stresses develop on the cut surfaces , which, however, depend on the orientation of the cut surfaces, i. H. their normal vectors . According to Cauchy's fundamental theorem , stress tensors represent this dependency by mapping the normals of the intersection surfaces linearly to the intersection stresses. The stress tensor is fundamental for the formulation of the laws of nature in their form valid at the material point.

The balance equations of mechanics describe the effect of the outside world on a body and the resulting change in physical quantities. These quantities are mass , momentum , angular momentum and energy . The second law of thermodynamics is taken into account in the form of the Clausius-Duhem inequality. The laws of nature formulated in mechanics for extended bodies are expressed in continuum mechanics as global integral equations, from which local differential equations can be derived with suitable assumptions , which must be fulfilled at every point or particle.

The local mass balance states that the density at the material point is constant over time. The local momentum balance sets the specific momentum change in relation to the specific gravity and to the drive through an increase in voltage. The angular momentum balance is reduced to the requirement for the symmetry of the stress tensor. The energy balance states that the internal energy changes due to internal heat sources, the specific heat input and the specific voltage output at distortion speeds. With isothermal processes, the Clausius-Duhem inequality ultimately requires that the production of Helmholtz free energy must not exceed the specific voltage output. This condition should be interpreted less as a restriction of physical processes, but rather as a requirement for material models: It must be ensured that the local forms of the Clausius-Duhem inequality are fulfilled by the constitutive equations for any processes.

Material theory

The mathematical formulation of the laws of nature does not make any statements about the individual properties of the body - whether they are solid, liquid or gaseous, for example - and is therefore not sufficient to clearly determine the movements of the body. This also requires constitutive equations that determine the material-specific response of the body, e.g. B. to an external force describe. In this case, a relationship between the deformations of the body and the reaction forces must be given. Material theory deals with these relationships and how they are implemented in a material model. The aim of a material model is to describe the essential aspects of the material behavior, whereby what is essential is determined by the observer. Substance or material laws, as material models are sometimes called, do not have the general validity of physical laws.

Classical continuum mechanics considers simple materials in which the previous movement (determinism) determines the behavior at a material point completely from its environment (locality), regardless of the state of movement of the observer (objectivity). So simple materials are deterministic, local and objective. Their properties can be represented with material constraints, material symmetries and constitutive equations. Material constraints limit the deformation possibilities of a material, such as B. the incompressibility does. Material symmetries describe the directional dependence of the material as it is e.g. B. is given in wood. The constitutive equations finally establish a relation between the strains and the stresses.

The six material models of classical material theory are the ideal gas , Newton's fluid , Hooke's law , viscoelasticity, plasticity and viscoplasticity. The Euler equations , the Navier-Stokes equations and the Navier-Cauchy equations are derived from the first three models .

Tensor calculus

Linear mapping of a vector by a tensor . ${\displaystyle {\vec {v}}}$ ${\displaystyle \mathbf {T} }$

The most important mathematical aid in continuum mechanics is tensor calculus, the knowledge of which cannot generally be assumed. Only the calculation rules used in this article are briefly presented here.

The tensors most commonly used in continuum mechanics are second-order tensors, which linearly map geometric vectors from the three-dimensional Euclidean vector space onto one another. The vectors are generally rotated and stretched, see figure on the right. The component-wise representation applies to these tensors

${\displaystyle \mathbf {T} =\sum _{i,j=1}^{3}T^{ij}{\vec {g}}_{i}\otimes {\vec {G}}_{j}}$

with components of the tensor which belong to vectors linked with the dyadic product " " from two vector space bases or the assumed vector space. Different bases are used in the description with convective coordinates . Here it is sufficient to identify the bases and with the standard basis so that every tensor can be equated with its matrix representation : ${\displaystyle T^{ij}}$ ${\displaystyle \otimes }$ ${\displaystyle {\vec {g}}_{1,2,3}}$ ${\displaystyle {\vec {G}}_{1,2,3}}$ ${\displaystyle {\vec {G}}_{1,2,3}}$ ${\displaystyle {\vec {g}}_{1,2,3}}$ ${\displaystyle {\vec {e}}_{1,2,3}}$

${\displaystyle \mathbf {T} =\sum _{i,j=1}^{3}T_{ij}{\vec {e}}_{i}\otimes {\vec {e}}_{j}={\begin{pmatrix}T_{11}&T_{12}&T_{13}\\T_{21}&T_{22}&T_{23}\\T_{31}&T_{32}&T_{33}\end{pmatrix}}}$

Let another tensor and a vector be given for the component-wise representations ${\displaystyle \mathbf {S} }$ ${\displaystyle {\vec {v}}}$

${\displaystyle \mathbf {S} =\sum _{i,j=1}^{3}S_{ij}{\vec {e}}_{i}\otimes {\vec {e}}_{j}\quad {\textsf {und}}\quad {\vec {v}}=\sum _{i=1}^{3}v_{i}{\vec {e}}_{i}}$

be valid. The operations used in the article are defined as follows:

operator	definition
Addition and subtraction	${\displaystyle \mathbf {S} \pm \mathbf {T} :=\sum _{i,j=1}^{3}(S_{ij}\pm T_{ij}){\vec {e}}_{i}\otimes {\vec {e}}_{j}}$
Multiplication by a scalar x	${\displaystyle x\;\mathbf {T} :=\sum _{i,j=1}^{3}xT_{ij}{\vec {e}}_{i}\otimes {\vec {e}}_{j}}$
Tensor product	${\displaystyle \mathbf {S} \cdot \mathbf {T} :=\sum _{i,j,k=1}^{3}(S_{ik}T_{kj}){\vec {e}}_{i}\otimes {\vec {e}}_{j}}$
Transposition	${\displaystyle {\begin{aligned}\mathbf {T} ^{\top }:=&\sum _{i,j=1}^{3}T_{ij}{\vec {e}}_{j}\otimes {\vec {e}}_{i}={\begin{pmatrix}T_{11}&T_{21}&T_{31}\\T_{12}&T_{22}&T_{32}\\T_{13}&T_{23}&T_{33}\end{pmatrix}}\\(\mathbf {S\cdot T} )^{\top }=&\mathbf {T^{\top }\cdot S^{\top }} \end{aligned}}}$
Transformation of a vector with the scalar product " " of vectors ${\displaystyle \cdot }$	${\displaystyle \mathbf {T} \cdot {\vec {v}}:=\sum _{i,j=1}^{3}T_{ij}v_{j}{\vec {e}}_{i}\;,\quad {\vec {v}}\cdot \mathbf {T} =\mathbf {T} ^{\top }\cdot {\vec {v}}}$
Inversion	${\displaystyle {\begin{aligned}\mathbf {T} ^{-1}:\quad \mathbf {T} ^{-1}\cdot \mathbf {T} =&\mathbf {T\cdot T} ^{-1}=\mathbf {1} \\\left(\mathbf {T} ^{\top }\right)^{-1}=&\left(\mathbf {T} ^{-1}\right)^{\top }=\mathbf {T} ^{\top -1}\end{aligned}}}$
Frobenius dot product	${\displaystyle \mathbf {S} :\mathbf {T} :=\sum _{i,j=1}^{3}S_{ij}T_{ij}}$

Therein is the unit tensor . ${\displaystyle \mathbf {1} }$

Furthermore, the Fréchet derivation is required, which generalizes the differential calculus to vectors and tensors. The Fréchet derivative of a function according to the restricted linear operator , which - if it exists - in all directions the Gâteaux derivative corresponds, so ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle h}$

${\displaystyle {\mathcal {A}}(h)=\left.{\frac {\mathrm {d} }{\mathrm {d} s}}f(x+sh)\right|_{s=0}=\lim _{s\rightarrow 0}{\frac {f(x+sh)-f(x)}{s}}\quad \forall \;h}$

applies. In it and is scalar, vector or tensor valued but and of the same kind. Then will too ${\displaystyle s\in \mathbb {R} ,\;f\,,x}$ ${\displaystyle h}$ ${\displaystyle x}$ ${\displaystyle h}$

${\displaystyle {\mathcal {A}}={\frac {\mathrm {d} f}{\mathrm {d} x}}}$

written. Further definitions and calculation rules are given in the formulary tensor algebra and formulary tensoranalysis .

kinematics

→ Main article : Kinematics

Here only the specific continuum mechanical aspects are to be described, more can be looked up in the main article. In continuum mechanics, the kinematics gives transformation equations for quantities in the initial configuration into the corresponding quantities in the current configuration and derives distortion measures from them.

The material body

→ Main article : Configuration (mechanics)

The material body as the carrier of the physical processes equally fills parts of the space of our perception. In continuum mechanics, the body is mapped bijectively into a Euclidean vector space by means of configurations , whereby the properties of the body are continuously smeared over the space. With the help of this idealization , the body is described as a set of points in which gradients and integrals can be formed. ${\displaystyle \mathbb {V} ^{3}}$

This has two consequences:

1. There is a size scale below which the statements of continuum mechanics lose their validity. This size scale is above the dimensions of the representative volume element (RVE), from which identical copies of which the material body is thought to be built. The RVE of a crystal can be a unit cell , for example .
2. An internal point of the body always remains an internal point, which is why it is not possible to describe the propagation of cracks using statements from classical continuum mechanics. Fracture mechanics is concerned with the reaction of bodies to cracks and crack propagation , which in turn depends on the presence of a crack.

The following configurations are used for a body:

1. The reference configuration used to identify the material points . The initial configuration of the body at a set point in time is fixed in time and can and should serve as a reference configuration. Because this position has once been assumed by the body, this reference configuration provides an object of our perception. ${\displaystyle \kappa _{R}(P)}$ ${\displaystyle P}$ ${\displaystyle {\vec {X}}=\kappa _{0}(P)}$ ${\displaystyle {t}_{0}}$
2. The current configuration shows the deformed body at the moment . ${\displaystyle {\vec {x}}=\kappa _{t}(P)}$ ${\displaystyle t}$

Linking these configurations

${\displaystyle {\begin{array}{lll}{\vec {\chi }}:=\kappa _{t}\circ \kappa _{0}^{-1}:&V\subset \mathbb {V} ^{3}&\rightarrow v\subset \mathbb {V} ^{3}\\&{\vec {X}}&\mapsto {\vec {x}}\end{array}}}$

is called the movement function and should be continuously differentiable as often as is necessary in the respective context. The original image space is identified with the volume occupied by the body in the reference configuration and the image space with the volume occupied by the body in the current configuration. ${\displaystyle V}$ ${\displaystyle v}$

Material and spatial coordinates

The material coordinates of a material point are the components of its position vector in the initial configuration: ${\displaystyle {\vec {X}}}$ ${\displaystyle P}$

${\displaystyle {\vec {X}}=\kappa _{0}(P)\in V\subset \mathbb {V} ^{3}\,.}$

The current configuration gives the spatial coordinates of the material point in space at any point in time : ${\displaystyle {\vec {x}}}$ ${\displaystyle P}$

${\displaystyle {\vec {x}}=\kappa _{t}(P)=\kappa _{t}(\kappa _{0}^{-1}({\vec {X}}))=:{\vec {\chi }}({\vec {X}},t)\in v\subset \mathbb {V} ^{3}\,.}$

The movement function describes the trajectory of a material point through space when held . Because of the bijectivity, the motion function can be inverted at any time: ${\displaystyle {\vec {\chi }}({\vec {X}},t)}$ ${\displaystyle {\vec {X}}}$

${\displaystyle {\vec {X}}={\vec {\chi }}^{-1}({\vec {x}},t)\in V\subset \mathbb {V} ^{3}\,.}$

With a fixed point in space , the movement function delivers the streak line through the point in space. ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {\chi }}^{-1}({\vec {x}},t)}$

Because of the unambiguousness of the configurations in the description of the material body, all quantities assigned to a material point (e.g. density, temperature and speed) can be described as a function of its material or spatial coordinates. Unless otherwise stated, sizes in the material perspective are designated with capital letters or the index and those in spatial terms with lowercase letters. ${\displaystyle {(\;)}_{0}}$

Lagrangian approach

→ Main article : Lagrangian approach

If the movement of a material point is to be observed and which physical conditions prevail in it, it makes sense to write down the quantities assigned to the material point as a function of the material coordinates, because these are constant for each material point. This results in the material or Lagrangeian approach (according to Joseph-Louis Lagrange ), which is preferred in solid mechanics.

Euler's approach

→ Main article : Euler's approach

On the other hand, if the physical processes are to be followed at a fixed point in space, it makes sense to note the physical quantities as a function of the spatial coordinates. This is the spatial or Eulerian approach that is used in fluid mechanics.

Differential operators

In continuum mechanics, two differential operators , for the gradient and the divergence, are mainly used for the material and the spatial approach :

Field variable	Divergence DIV	Gradient GRAD
Scalar field ${\displaystyle \phi }$		${\displaystyle {\frac {\partial \phi }{\partial {\vec {X}}}}=\sum _{i=1}^{3}{\frac {\partial \phi }{\partial X_{i}}}{\vec {e}}_{i}}$
Vector field ${\displaystyle {\vec {\phi }}=\sum _{i=1}^{3}\phi _{i}{\vec {e}}_{i}}$	${\displaystyle \sum _{i=1}^{3}{\vec {e}}_{i}\cdot {\frac {\partial {\vec {\phi }}}{\partial X_{i}}}=\sum _{i=1}^{3}{\frac {\partial \phi _{i}}{\partial X_{i}}}}$	${\displaystyle {\frac {\partial {\vec {\phi }}}{\partial {\vec {X}}}}=\sum _{i,j=1}^{3}{\frac {\partial \phi _{i}}{\partial X_{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}}$
Tensor field ${\displaystyle {\boldsymbol {\phi }}=\sum _{i,j=1}^{3}\phi _{ij}{\vec {e}}_{i}\otimes {\vec {e}}_{j}}$	${\displaystyle \sum _{i=1}^{3}{\vec {e}}_{i}\cdot {\frac {\partial {\boldsymbol {\phi }}}{\partial X_{i}}}=\sum _{i,j=1}^{3}{\frac {\partial \phi _{ij}}{\partial X_{i}}}{\vec {e}}_{j}}$

The material operators DIV and GRAD contain the material derivatives according to the material coordinates . Corresponding definitions apply to the spatial operators div and grad in the spatial formulation, which include the spatial derivatives according to the spatial coordinates . ${\displaystyle {\vec {X}}}$ ${\displaystyle {\vec {x}}}$

Local and material time derivative

The time derivative of a quantity associated with a material point, e.g. B. the temperature , can be evaluated with a fixed point in space or a fixed material point . The former is the local time derivative, the latter the material or substantial derivative . Because the laws of nature refer to material points, the substantial time derivative is physically determining. ${\displaystyle T}$ ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {X}}}$

The partial derivative with a fixed point in space is the local time derivative, i.e. H. the rate of change that exists at a fixed point in space. ${\displaystyle {\frac {\partial }{\partial t}}T({\vec {x}},t)}$ ${\displaystyle {\vec {x}}}$

The material time derivative is the partial derivative according to the Lagrange perspective ${\displaystyle {\tfrac {\mathrm {D} }{\mathrm {D} t}}}$

${\displaystyle {\dot {T}}_{0}({\vec {X}},t):={\frac {\mathrm {D} }{\mathrm {D} t}}T_{0}({\vec {X}},t):=\left.{\frac {\mathrm {d} }{\mathrm {d} t}}T_{0}({\vec {X}},t)\right|_{{\vec {X}}\;{\text{fest}}}={\frac {\partial }{\partial t}}T_{0}({\vec {X}},t)}$

and is also marked here with the added point . The material time derivative is the rate of change of a field variable observable on a particle . In this example, a thermometer would continuously measure changes in temperature for just that one particle . ${\displaystyle {\vec {X}}}$ ${\displaystyle {\vec {X}}}$

In Euler's approach, the material time derivative is made up of the local and an additional convective part:

${\displaystyle {\frac {\mathrm {D} }{\mathrm {D} t}}T({\vec {\chi }}({\vec {X}},t),t)={\frac {\partial }{\partial {\vec {x}}}}T({\vec {x}},t)\cdot {\frac {\mathrm {D} }{\mathrm {D} t}}{\vec {\chi }}({\vec {X}},t)+{\frac {\partial }{\partial t}}T({\vec {x}},t)=\operatorname {grad} \;(T({\vec {x}},t))\cdot {\vec {v}}({\vec {x}},t)+{\frac {\partial }{\partial t}}T({\vec {x}},t)}$

The material coordinates belong to the particle that is currently at the location and has the speed at this point in time , and represents the convective part . The material time derivative of a vector quantity is formed in a completely analogous manner , for example the substantial acceleration: ${\displaystyle {\vec {X}}={\vec {\chi }}^{-1}({\vec {x}},t)}$ ${\displaystyle t}$ ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {v}}({\vec {x}},t)={\dot {\vec {\chi }}}({\vec {X}},t)}$ ${\displaystyle \operatorname {grad} (T)\cdot {\vec {v}}}$

${\displaystyle {\dot {\vec {v}}}={\frac {\mathrm {D} }{\mathrm {D} t}}{\vec {v}}={\frac {\partial }{\partial t}}{\vec {v}}+\operatorname {grad} ({\vec {v}})\cdot {\vec {v}}={\frac {\partial }{\partial t}}{\vec {v}}+({\vec {v}}\cdot \nabla ){\vec {v}}\,.}$

The latter notation with the Nabla operator is preferred in fluid mechanics. ${\displaystyle \nabla }$

The deformation gradient

→ Main article : Deformation gradient

Deformation gradient

The deformation gradient is the fundamental parameter for describing deformations that result from local changes in length and from changes in angle between material line elements. The deformation gradient transforms the tangential vectors on material lines in the initial configuration into the current configuration , see picture. The deformation gradient is calculated from the derivation of the motion function according to the material coordinates

${\displaystyle \mathbf {F} ({\vec {X}},t)=\operatorname {GRAD} ({\vec {\chi }}({\vec {X}},t))={\frac {\mathrm {d} \chi _{i}({\vec {X}},t)}{\mathrm {d} X_{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}={\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} {\vec {X}}}}}$

and can also use the directional derivative

${\displaystyle \mathbf {F} ({\vec {X}},t)\cdot \mathrm {d} {\vec {X}}=\left.{\frac {\mathrm {d} }{\mathrm {d} s}}{\vec {\chi }}{({\vec {X}}+s\;\mathrm {d} {\vec {X}},t)}\right|_{s=0}=\mathrm {d} {\vec {x}}}$

can be displayed, which illustrates its transformation properties of the line elements . ${\displaystyle \mathrm {d} {\vec {X}}}$

The deformation gradient also transforms the surface element , the normal of the surface area multiplied by the area, and the volume element from the initial configuration to the current configuration : ${\displaystyle {\vec {N}}\mathrm {d} A}$ ${\displaystyle \mathrm {d} A}$ ${\displaystyle {\vec {N}}}$ ${\displaystyle \mathrm {d} V}$

${\displaystyle {\begin{array}{lcl}{\vec {n}}\mathrm {d} a&=&\det(\mathbf {F} ){\mathbf {F} }^{\top -1}\cdot {\vec {N}}\mathrm {d} A\\\mathrm {d} v&=&\det(\mathbf {F} )\mathrm {d} V\end{array}}\,.}$

The operator gives the determinant and the transposed inverse . With these elements, integrals in the initial and momentary configuration (synonymous: in the material and spatial formulation) can be converted into one another. ${\displaystyle \det(\;)}$ ${\displaystyle (\;)^{\top -1}}$

Strain tensors

→ Main article : strain tensor

Illustration of the polar decomposition

With the help of the deformation gradient, the distortion dimensions are defined. The polar decomposition of the deformation gradient splits the deformation locally into a pure rotation, mediated by the orthogonal rotation tensor , and a pure stretching, mediated by the symmetrical positive definite right and left stretch tensor and , see picture. The spatial tensor is capitalized here to avoid confusion with the speed , which is sometimes also written in bold letters. ${\displaystyle \mathbf {F} =\mathbf {R\cdot U} =\mathbf {V\cdot R} }$ ${\displaystyle \mathbf {R} }$ ${\displaystyle \mathbf {U} }$ ${\displaystyle \mathbf {V} }$ ${\displaystyle \mathbf {V} }$ ${\displaystyle {\vec {v}}}$

The distance sensors are used to define a variety of strain tensors, e.g. B. the Biot strains

${\displaystyle \mathbf {E} _{N}=\mathbf {U} -\mathbf {1} \,,}$

which are sometimes called nominal elongations , the Hencky elongations

${\displaystyle \mathbf {E} _{H}=\ln(\mathbf {U} )\,,}$

(calculated by means of the main axis transformation of , formation of the logarithms of the diagonal elements and inverse transformation), the Green- Lagrange strains ${\displaystyle \mathbf {U} }$

${\displaystyle \mathbf {E} ={\tfrac {1}{2}}(\mathbf {U\cdot U} -\mathbf {1} )={\tfrac {1}{2}}({\mathbf {F} }^{\top }\cdot \mathbf {F} -\mathbf {1} )}$

and Euler-Almansi strains

${\displaystyle \mathbf {e} ={\tfrac {1}{2}}(\mathbf {1} -\mathbf {V} ^{-1}\cdot \mathbf {V} ^{-1})={\tfrac {1}{2}}(\mathbf {1} -{\mathbf {F} }^{\top -1}\cdot \mathbf {F} ^{-1})\,.}$

As above stands for the unit tensor . The latter strain tensors are motivated by comparing two material line elements and in the point : ${\displaystyle \mathbf {1} }$ ${\displaystyle \mathrm {d} {\vec {X}}}$ ${\displaystyle \mathrm {d} {\vec {Y}}}$ ${\displaystyle {\vec {X}}}$

${\displaystyle {\begin{array}{rclcl}\mathrm {d} {\vec {x}}\cdot \mathrm {d} {\vec {y}}-\mathrm {d} {\vec {X}}\cdot \mathrm {d} {\vec {Y}}&=&(\mathbf {F} \cdot \mathrm {d} {\vec {X}})\cdot (\mathbf {F} \cdot \mathrm {d} {\vec {Y}})-\mathrm {d} {\vec {X}}\cdot \mathrm {d} {\vec {Y}}&=&2\mathrm {d} {\vec {X}}\cdot \mathbf {E} \cdot \mathrm {d} {\vec {Y}}\\&=&\mathrm {d} {\vec {x}}\cdot \mathrm {d} {\vec {y}}-(\mathbf {F} ^{-1}\cdot \mathrm {d} {\vec {x}})\cdot (\mathbf {F} ^{-1}\cdot \mathrm {d} {\vec {y}})&=&2\mathrm {d} {\vec {x}}\cdot \mathbf {e} \cdot \mathrm {d} {\vec {y}}\end{array}}}$

Distortion Rates

From the material derivation of time

${\displaystyle {\begin{array}{lclcl}{\dfrac {\mathrm {D} }{\mathrm {D} t}}(\mathrm {d} {\vec {x}}\cdot \mathrm {d} {\vec {y}}-\mathrm {d} {\vec {X}}\cdot \mathrm {d} {\vec {Y}})&=&{\dfrac {\mathrm {D} }{\mathrm {D} t}}[(\mathbf {F} \cdot \mathrm {d} {\vec {X}})\cdot (\mathbf {F} \cdot \mathrm {d} {\vec {Y}})]\\&=&({\dot {\mathbf {F} }}\cdot \mathrm {d} {\vec {X}})\cdot (\mathbf {F} \cdot \mathrm {d} {\vec {Y}})+(\mathbf {F} \cdot \mathrm {d} {\vec {X}})\cdot ({\dot {\mathbf {F} }}\cdot \mathrm {d} {\vec {Y}})&=:&2\mathrm {d} {\vec {X}}\cdot {\dot {\mathbf {E} }}\cdot \mathrm {d} {\vec {Y}}\\&=&({\dot {\mathbf {F} }}\cdot \mathbf {F} ^{-1}\cdot \mathrm {d} {\vec {x}})\cdot \mathrm {d} {\vec {y}}+\mathrm {d} {\vec {x}}\cdot ({\dot {\mathbf {F} }}\cdot \mathbf {F} ^{-1}\cdot \mathrm {d} {\vec {y}})&=:&2\mathrm {d} {\vec {x}}\cdot \mathbf {d} \cdot \mathrm {d} {\vec {y}}\end{array}}}$

derive the material strain velocity tensor

${\displaystyle {\dot {\mathbf {E} }}={\frac {1}{2}}({\dot {\mathbf {F} }}^{\top }\cdot \mathbf {F} +\mathbf {F} ^{\top }\cdot {\dot {\mathbf {F} }})}$

and the spatial

${\displaystyle \mathbf {d} ={\tfrac {1}{2}}({\dot {\mathbf {F} }}\cdot \mathbf {F} ^{-1}+\mathbf {F} ^{\top -1}\cdot {\dot {\mathbf {F} }}^{\top })}$

which disappear exactly when there are rigid body movements.

The spatial strain velocity tensor is the symmetrical part of the spatial velocity gradient : ${\displaystyle \mathbf {d} }$ ${\displaystyle \mathbf {l} }$

${\displaystyle \mathbf {l} :=\mathrm {grad} ({\vec {v}}({\vec {x}},t))={\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} {\vec {x}}}}={\frac {\mathrm {d} {\dot {\vec {\chi }}}}{\mathrm {d} {\vec {X}}}}\cdot {\frac {\mathrm {d} {\vec {X}}}{\mathrm {d} {\vec {x}}}}={\dot {\mathbf {F} }}\cdot \mathbf {F} ^{-1}\quad \rightarrow \quad \mathbf {d} ={\frac {1}{2}}(\mathbf {l} +\mathbf {l} ^{\top })}$

Geometric linearization

→ Main article : Geometric linearization

Comparison of different strain masses in the homogeneous stretching of a straight bar of length L to length u + L

The equations of continuum mechanics for solids are considerably simplified if small displacements can be assumed. Displacements are the difference between the position vectors of a particle in the current configuration and its initial position : ${\displaystyle {\vec {x}}={\vec {\chi }}({\vec {X}},t)}$ ${\displaystyle {\vec {X}}}$ ${\displaystyle {\vec {X}}}$

${\displaystyle {\vec {u}}={\vec {\chi }}({\vec {X}},t)-{\vec {X}}=:\left({\begin{array}{c}u({\vec {X}},t)\\v({\vec {X}},t)\\w({\vec {X}},t)\end{array}}\right)}$

and the displacement gradient is the tensor

${\displaystyle \mathbf {H} =\operatorname {GRAD} \;{\vec {u}}=\mathbf {F} -\mathbf {1} =\left({\begin{array}{ccc}{\frac {\partial u}{\partial X}}&{\frac {\partial u}{\partial Y}}&{\frac {\partial u}{\partial Z}}\\[1ex]{\frac {\partial v}{\partial X}}&{\frac {\partial v}{\partial Y}}&{\frac {\partial v}{\partial Z}}\\[1ex]{\frac {\partial w}{\partial X}}&{\frac {\partial w}{\partial Y}}&{\frac {\partial w}{\partial Z}}\end{array}}\right)\,.}$

If is a characteristic dimension of the body, then both and are required for small displacements , so that all terms that contain higher powers of or can be neglected. In the case of small displacements, it is no longer necessary to differentiate between Lagrange's and Euler's approaches, so that the spatial and material coordinates no longer have to be kept apart. this leads to ${\displaystyle L_{0}}$ ${\displaystyle \left|{\vec {u}}\right|\ll L_{0}}$ ${\displaystyle \|\mathbf {H} \|\ll 1}$ ${\displaystyle {\vec {u}}}$ ${\displaystyle \mathbf {H} }$ ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {X}}}$

${\displaystyle \mathbf {F} =\mathbf {1} +\mathbf {H} ,\quad \mathbf {F} ^{-1}\approx \mathbf {1} -\mathbf {H} ,\quad \det(\mathbf {F} )\approx 1+\operatorname {Sp} (\mathbf {H} ),\quad \mathbf {E} \approx \mathbf {e} \approx \mathbf {E} _{N}\approx \mathbf {E} _{H}\approx {\boldsymbol {\varepsilon }}:={\tfrac {1}{2}}(\mathbf {H} +\mathbf {H} ^{\top })\,.}$

This means that all listed distortion measures are transferred to the linearized distortion tensor in the case of small displacements . The linearized strain tensor ${\displaystyle {\boldsymbol {\varepsilon }}}$

${\displaystyle {\boldsymbol {\varepsilon }}={\tfrac {1}{2}}(\mathbf {H} +\mathbf {H} ^{\top })=\left({\begin{array}{ccc}{\frac {\partial u}{\partial x}}&{\frac {1}{2}}\left({\frac {\partial u}{\partial y}}+{\frac {\partial v}{\partial x}}\right)&{\frac {1}{2}}\left({\frac {\partial u}{\partial z}}+{\frac {\partial w}{\partial x}}\right)\\[1ex]{\frac {1}{2}}\left({\frac {\partial u}{\partial y}}+{\frac {\partial v}{\partial x}}\right)&{\frac {\partial v}{\partial y}}&{\frac {1}{2}}\left({\frac {\partial v}{\partial z}}+{\frac {\partial w}{\partial y}}\right)\\[1ex]{\frac {1}{2}}\left({\frac {\partial u}{\partial z}}+{\frac {\partial w}{\partial x}}\right)&{\frac {1}{2}}\left({\frac {\partial v}{\partial z}}+{\frac {\partial w}{\partial y}}\right)&{\frac {\partial w}{\partial z}}\end{array}}\right)}$

is also called engineering expansion, because in many technical applications there are small expansions or they have to be kept small for safety reasons. This geometrically linear view is permissible for values up to 3–8%, see picture. If there are no small displacements, we speak of finite or large displacements. ${\displaystyle \|\mathbf {H} \|}$

Sometimes geometrical linearization is only required and dropped so that large translations are permitted with only small rotations and expansions. Then, as before, a distinction must be made between Lagrange's and Euler's approach. ${\displaystyle \|\mathbf {H} \|\ll 1}$ ${\displaystyle \left|{\vec {u}}\right|\ll L_{0}}$

Laws of nature

The laws of nature formulated in mechanics for extended bodies are expressed in continuum mechanics as global integral equations, from which local (differential) equations can be derived with suitable continuity assumptions , which must be fulfilled at every material point. Further principles can then be motivated by means of equivalence transformations of the local equations. The global and local equations can also be related to the spatial or the material quantities, so that there are four equivalent formulations for each law . The formulas used here and others are summarized in the Tensoranalysis formula collection .

The balance equations of mechanics describe the effect of the outside world on a body and the resulting change in physical quantities. These quantities are mass , momentum , angular momentum and energy . In addition to the external influences known in mechanics, there are also internal sources and sinks in the continuum, e.g. B. gravity is an internal source of tension . In closed systems , where by definition an interaction with the outside world is excluded, the balance equations become conservation laws. The second law of thermodynamics is taken into account in the form of the Clausius-Duhem inequality.

Stress tensors

→ Main article : Stress tensor

Sectional stresses in the plane stress state depending on the normal to the cut surface. Red: normal in x-direction, blue: normal in y-direction.

The concept of the stress tensor, which represents the stresses in bodies due to external loads, is fundamental for the formulation of the balance equations . Newton's second law describes the reaction of a body to an external force . In reality and in continuum mechanics, such forces are always introduced over an area, i.e. H. Stress vectors ( vectors with the dimension force per area) act on a part of the surface of the body and are propagated in the body as stresses. Now the body can be mentally cut up so that cutting stresses develop on the cut surfaces , which, however, depend on the orientation of the cut surfaces, i. H. their normal vectors , see figure on the right. ${\displaystyle {\vec {t}}}$

On a cut-free (infinitesimal) small tetrahedron , the volume forces and the change in momentum as third-order terms are negligibly small compared to the superficial cutting stresses, which are second-order terms in the dimensions of the tetrahedron. From the equilibrium at the tetrahedron, it follows that the relationship between the normal and the stress vectors must be linear, which is the content of Cauchy's fundamental theorem :

${\displaystyle {\vec {t}}={\boldsymbol {\sigma }}^{\top }\cdot {\vec {n}}}$

Cauchy's stress tensor transforms the normal to the intersection into the stress vector. When transferring this relationship into Lagrange's approach, the change in the surface elements must also be taken into account: ${\displaystyle {\boldsymbol {\sigma }}}$ ${\displaystyle {\vec {n}}}$

${\displaystyle {\begin{array}{rcl}{\vec {t}}\,\mathrm {d} a&=&{\boldsymbol {\sigma }}^{\top }\cdot {\vec {n}}\,\mathrm {d} a={\boldsymbol {\sigma }}^{\top }\cdot \det(\mathbf {F} )\mathbf {F} ^{\top -1}\cdot {\vec {N}}\,\mathrm {d} A=:\mathbf {N} ^{\top }\cdot {\vec {N}}\,\mathrm {d} A=:{\vec {t}}_{0}\,\mathrm {d} A\\\Leftrightarrow \mathbf {N} &=&\det(\mathbf {F} )\mathbf {F} ^{-1}\cdot {\boldsymbol {\sigma }}\end{array}}}$

The stress tensor is called the nominal stress tensor and represents the stresses related to the initial area. The transpose of the nominal stress tensor is the first Piola-Kirchhoff stress tensor ${\displaystyle \mathbf {N} }$

${\displaystyle \mathbf {P} :=\mathbf {N} ^{\top }\,.}$

The second Piola-Kirchhoff stress tensor will be added later

${\displaystyle {\tilde {\mathbf {T} }}:=\det(\mathbf {F} )\mathbf {F} ^{-1}\cdot {\boldsymbol {\sigma }}\cdot \mathbf {F} ^{\top -1}=\mathbf {N} \cdot \mathbf {F} ^{\top -1}}$

needed.

In the case of small distortions, there is no need to distinguish between these stress tensors.

Mass balance

Let the density be in the spatial and that in the material description. Assuming that there are no sources of mass of any form, the mass balance means that the mass of a body ${\displaystyle \rho ({\vec {x}},t)}$ ${\displaystyle \rho _{0}({\vec {X}},t)}$ ${\displaystyle m}$

${\displaystyle m=\int _{v}\rho \,\mathrm {d} v=\int _{V}\rho _{0}\,\mathrm {d} V}$

is constant over time:

	Lagrangian approach	Euler's approach
global shape	${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}m={\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V}\rho _{0}\,\mathrm {d} V=0}$	${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}m={\frac {\mathrm {d} }{\mathrm {d} t}}\int _{v}\rho \,\mathrm {d} v=0}$
local shape	${\displaystyle {\dot {\rho }}_{0}=0}$	${\displaystyle {\frac {\partial }{\partial t}}\rho +\operatorname {div} (\rho {\vec {v}})=\underbrace {{\frac {\partial \rho }{\partial t}}+\operatorname {grad} (\rho )\cdot {\vec {v}}} _{={\dot {\rho }}}+\rho \,\operatorname {div} ({\vec {v}})={\dot {\rho }}+\rho \operatorname {div} ({\vec {v}})=0}$

The local forms are called the continuity equation . In the local Eulerian formulation, the product rule was

${\displaystyle \operatorname {div} (\rho {\vec {v}})=\operatorname {grad} (\rho )\cdot {\vec {v}}+\rho \,\operatorname {div} ({\vec {v}})}$

and the material time derivative of density used. ${\displaystyle {\dot {\rho }}}$

Momentum balance

→ Main article : First Cauchy-Euler law of motion

The law of momentum says that the change in momentum is equal to the forces acting from outside (volume-distributed or superficial):

	Lagrangian approach	Euler's approach
global shape	${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V}\rho _{0}{\dot {\vec {\chi }}}\,\mathrm {d} V=\int _{V}\rho _{0}{\vec {k}}_{0}\,\mathrm {d} V+\int _{A}{\vec {t}}_{0}\,\mathrm {d} A}$	${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\int _{v}\rho {\vec {v}}\,\mathrm {d} v=\int _{v}\rho {\vec {k}}\,\mathrm {d} v+\int _{a}{\vec {t}}\,\mathrm {d} a}$
local shape	${\displaystyle \rho _{0}{\ddot {\vec {\chi }}}=\rho _{0}{\vec {k}}_{0}+\operatorname {DIV} \;\mathbf {N} }$	${\displaystyle \rho {\dot {\vec {v}}}=\rho {\dfrac {\partial }{\partial t}}{\vec {v}}+\rho \operatorname {grad} ({\vec {v}})\cdot {\vec {v}}=\rho {\vec {k}}+\operatorname {div} \;{\boldsymbol {\sigma }}}$

The vector stands for a gravitational acceleration as it is the force of gravity , and are surface tensions on the surface or the body at the time or . ${\displaystyle {\vec {k}}_{(0)}}$ ${\displaystyle {\vec {t}}_{(0)}}$ ${\displaystyle A}$ ${\displaystyle a}$ ${\displaystyle t_{0}}$ ${\displaystyle t}$

Angular momentum balance

→ Main article : Second Cauchy-Euler law of motion

The law of angular momentum states that the change in angular momentum is equal to the external torques (volume-distributed or superficial):

Lagrangian approach	${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V}({\vec {\chi }}-{\vec {c}}){\times }\rho _{0}{\dot {\vec {\chi }}}\,\mathrm {d} V=\int _{V}({\vec {\chi }}-{\vec {c}})\times \rho _{0}{\vec {k}}_{0}\,\mathrm {d} V+\int _{A}({\vec {\chi }}-{\vec {c}})\times {\vec {t}}_{0}\,\mathrm {d} A}$
Euler's approach	${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\int _{v}({\vec {x}}-{\vec {c}}){\times }\rho {\vec {v}}\,\mathrm {d} v=\int _{v}({\vec {x}}-{\vec {c}})\times \rho {\vec {k}}\,\mathrm {d} v+\int _{a}({\vec {x}}-{\vec {c}})\times {\vec {t}}\,\mathrm {d} a}$

The arithmetic symbol forms the cross product and is an arbitrary, temporally fixed position vector. ${\displaystyle \times }$ ${\displaystyle {\vec {c}}}$

The local forms are reduced to the requirement for the symmetry of the second Piola-Kirchhoff and Cauchy stress tensor:

Lagrangian approach	${\displaystyle {\tilde {\mathbf {T} }}={\tilde {\mathbf {T} }}^{\top }}$
Euler's approach	${\displaystyle {\boldsymbol {\sigma }}={\boldsymbol {\sigma }}^{\top }}$

Energy balance

The thermomechanical energy balance states that the change in the total energy of a body is equal to the sum of the heat input and the power of all external forces. The total energy is made up of the internal energy with the specific internal energy and the kinetic energy : ${\displaystyle \int _{V}\rho _{0}u_{0}\,\mathrm {d} V}$ ${\displaystyle u_{0}}$ ${\displaystyle \int _{V}{\frac {\rho _{0}}{2}}{\dot {\vec {\chi }}}\cdot {\dot {\vec {\chi }}}\,\mathrm {d} V}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V}\rho _{0}u_{0}\,\mathrm {d} V+{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V}{\frac {\rho _{0}}{2}}{\dot {\vec {\chi }}}\cdot {\dot {\vec {\chi }}}\,\mathrm {d} V=\int _{V}\rho _{0}{\vec {k}}_{0}\cdot {\dot {\vec {\chi }}}\,\mathrm {d} V+\int _{A}{\vec {t}}_{0}\cdot {\dot {\vec {\chi }}}\,\mathrm {d} A+\int _{V}\rho _{0}r_{0}\,\mathrm {d} V-\int _{A}{\vec {N}}\cdot {\vec {q}}_{0}\,\mathrm {d} A\,.}$

It contains internal heat sources of the body, the heat flow per area and the normal directed outwards on the surface element of the body . The negative sign of the last term provides an energy supply when the heat flow is directed into the body. ${\displaystyle r_{0}}$ ${\displaystyle {\vec {q}}_{0}}$ ${\displaystyle {\vec {N}}}$ ${\displaystyle \mathrm {d} A}$

In Euler's approach, the global energy balance is called:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\int _{v}\rho u\,\mathrm {d} v+{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{v}{\frac {\rho }{2}}{\vec {v}}\cdot {\vec {v}}\,\mathrm {d} v=\int _{v}\rho {\vec {k}}\cdot {\vec {v}}\,\mathrm {d} v+\int _{a}{\vec {t}}\cdot {\vec {v}}\,\mathrm {d} a+\int _{v}\rho r\,\mathrm {d} v-\int _{a}{\vec {n}}\cdot {\vec {q}}\,\mathrm {d} a\,.}$

The local forms are:

Lagrangian approach	${\displaystyle {\dot {u}}_{0}={\frac {1}{\rho _{0}}}{\tilde {\mathbf {T} }}:{\dot {\mathbf {E} }}-{\frac {1}{\rho _{0}}}\operatorname {DIV} \;{\vec {q}}_{0}+r_{0}}$
Euler's approach	${\displaystyle {\dot {u}}={\frac {1}{\rho }}{\boldsymbol {\sigma }}:\mathbf {d} -{\frac {1}{\rho }}\operatorname {div} \;{\vec {q}}+r}$

Principle of d'Alembert in the Lagrange version

→ Main article : d'Alembert's principle

The principle of d'Alembert in the Lagrange version (i.e. in material representation) is of fundamental importance for the solution of initial boundary value problems in continuum mechanics, in particular the displacement method in the finite element method . The principle of d'Alembert in the Lagrange version is a statement equivalent to the local momentum balance (in material representation) about the work of forces and tensions occurring in the system on virtual displacements or virtual distortions .

Under the displacement of a material point in the difference vector is from its current position and its starting position understood: . Virtual displacements are independent, imaginary, largely arbitrary, differential displacements that are compatible with the geometrical bonds of the body. The virtual displacements must disappear wherever displacement boundary conditions of the body are given. Let be the part of the surface of the body on which displacement boundary conditions are explained. For a material vector field of the virtual displacements , then ${\displaystyle {\vec {u}}}$ ${\displaystyle {\vec {X}}}$ ${\displaystyle {\vec {x}}={\vec {\chi }}({\vec {X}},t)}$ ${\displaystyle {\vec {X}}}$ ${\displaystyle {\vec {u}}={\vec {x}}-{\vec {X}}}$ ${\displaystyle \delta {\vec {u}}}$ ${\displaystyle {\vec {u}}}$ ${\displaystyle {A}^{u}}$ ${\displaystyle A}$ ${\displaystyle \delta {\vec {u}}({\vec {X}})}$

${\displaystyle \delta {\vec {u}}({\vec {X}})={\vec {0}}{\quad \forall \;}{\vec {X}}{\in }{A}^{u}}$

to promote. In no surface tension can then be specified. This is why it refers to the part of the surface of the body on which surface tension (can) act. Analogous to the distortions based on the displacements , virtual distortions develop from the virtual displacements , which is why these should be continuously differentiable at least once: ${\displaystyle {A}^{u}}$ ${\displaystyle {A}^{\sigma }=A\setminus A^{u}}$ ${\displaystyle {\vec {u}}}$ ${\displaystyle \delta \mathbf {E} }$ ${\displaystyle \delta {\vec {u}}}$

${\displaystyle \delta \mathbf {E} :={\frac {1}{2}}(\mathbf {F} ^{\top }\cdot \delta \mathbf {F} +\delta \mathbf {F} ^{\top }\cdot \mathbf {F} )=\left.{\frac {\mathrm {d} }{\mathrm {d} s}}\mathbf {E} (\mathbf {F} +s\;\delta \mathbf {F} )\right|_{s=0}\,.}$

This is where the virtual deformation gradient is. ${\displaystyle \delta \mathbf {F} :=\operatorname {GRAD} (\delta {\vec {u}})}$

By scalar multiplying the local momentum balance in Lagrange's formulation with the virtual displacements and integrating the result over the volume of the body

${\displaystyle \int _{V}\delta {\vec {u}}\cdot (\rho _{0}{\vec {k}}_{0}+\operatorname {DIV} \;\mathbf {N} -\rho _{0}{\ddot {\vec {\chi }}})\,\mathrm {d} V=0\quad \forall \;\delta {\vec {u}}\in {\mathcal {V}}\,.}$

The set contains all permissible virtual displacements. Because this equation applies to all possible virtual displacements , the volume integral only disappears if and only if the term in brackets disappears everywhere. This is also called the “weak formulation” of the momentum balance. Further transformation of the integral equation by using Cauchy's fundamental theorem , Gauss’s integral theorem , the product rules for divergence and the symmetry of the second Piola-Kirchhoff stress tensor leads to the principle of d'Alembert in the Lagrange version ${\displaystyle {\mathcal {V}}}$ ${\displaystyle \delta {\vec {u}}\in {\mathcal {V}}}$

${\displaystyle \int _{V}\delta {\vec {u}}\cdot {\rho }_{0}{\ddot {\vec {u}}}\,{\text{d}}V+\int _{V}{\tilde {\mathbf {T} }}:\delta \mathbf {E} \,{\text{d}}V=\int _{{A}^{\sigma }}\delta {\vec {u}}\cdot {\vec {t}}_{0}\,{\text{d}}A+\int _{V}\delta {\vec {u}}\cdot \rho _{0}{\vec {k}}_{0}\,{\text{d}}V\quad \forall \;\delta {\vec {u}}\in {\mathcal {V}}\,.}$

On the left side is the virtual work of the inertial forces and the virtual deformation work and on the right side the virtual work of the external forces (surface and volume distributed). The exact derivation can be looked up in the conclusions from the Cauchy-Euler laws of motion .

Clausius-Duhem inequality

→ Main article : Clausius-Duhem inequality

The Clausius-Duhem inequality follows from the application of the second law of thermodynamics to solids. With the assumptions of entropy production and entropy flow , which are justified in quasi-stationary processes, the Clausius-Duhem inequality is derived from the second law of thermodynamics with the specific entropy : ${\displaystyle r/T}$ ${\displaystyle {\vec {q}}/T}$ ${\displaystyle s}$

	Lagrangian approach	Euler's approach
global shape	${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V}s_{0}\,\rho _{0}\mathrm {d} V\geq \int _{V}{\frac {r_{0}}{T}}\,\rho _{0}\mathrm {d} V-\int _{A}{\frac {{\vec {q}}_{0}}{T}}\cdot {\vec {N}}\,\mathrm {d} A}$	${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\int _{v}s\,\rho \mathrm {d} V\geq \int _{v}{\frac {r}{T}}\,\rho \mathrm {d} v-\int _{a}{\frac {\vec {q}}{T}}\cdot {\vec {n}}\,\mathrm {d} a}$
local shape	${\displaystyle {\frac {1}{\rho _{0}}}{\tilde {\mathbf {T} }}:{\dot {\mathbf {E} }}-{\dot {\psi }}_{0}-s_{0}{\dot {T}}_{0}-{\frac {{\vec {q}}_{0}}{\rho _{0}T_{0}}}\cdot \operatorname {GRAD} \;T_{0}\geq 0}$	${\displaystyle {\frac {1}{\rho }}{\boldsymbol {\sigma }}:\mathbf {d} -{\dot {\psi }}-s{\dot {T}}-{\frac {\vec {q}}{\rho T}}\cdot \operatorname {grad} \;T\geq 0}$

Here again the negative sign of the last term is due in the global forms of the outwardly directed normals, see #energy balance above. The Helmholtz free energy :

${\displaystyle \psi =u-sT\quad \rightarrow \quad {\dot {\psi }}+s{\dot {T}}={\dot {u}}-{\dot {s}}T}$

replaces the internal energy in the local forms. In the important special case in which temperature changes can be neglected, the local forms are simplified to:

	Lagrangian approach	Euler's approach
local shape	${\displaystyle {\frac {1}{\rho _{0}}}{\tilde {\mathbf {T} }}:{\dot {\mathbf {E} }}-{\dot {\psi }}_{0}\geq 0}$	${\displaystyle {\frac {1}{\rho }}{\boldsymbol {\sigma }}:\mathbf {d} -{\dot {\psi }}\geq 0}$

The scalar product of the voltages with the distortion speeds is the specific voltage power and that part of it that goes beyond the production of free energy is dissipated . The local forms of the Clausius-Duhem inequality are to be interpreted less as a restriction of physical processes, but rather as a requirement for material models: It must be ensured that the local forms of the Clausius-Duhem inequality are fulfilled by the constitutive equations for any processes.

Material theory

Material theory deals with the individual characteristics of materials and the creation of mathematical models of them. The aim of a material model is to describe the essential aspects of the material behavior, whereby what is essential is determined by the observer. Substance or material laws, as material models are sometimes called, do not have the general validity of physical laws. In the material modeling, the dependence of the stresses on the strains (or vice versa) is to be described in the form of equations so that the deformation of bodies made of this material can be calculated. Classical continuum mechanics considers simple materials whose properties are represented with material constraints, material symmetries and constitutive equations.

Simple materials

The material theory of classical continuum mechanics presupposes determinism , locality and objectivity of the material. Determinism means that the current state of a body in one of its material points is completely and unambiguously determined by the past movement of the body. Locality restricts the sphere of influence of the outside world on the current state of tension in a material point to its immediate surroundings, effects propagate from one material point to the next. Material objectivity means that the material response is independent of the observer's reference system, see Euclidean transformation . Materials that meet these three requirements are simply called . In the case of simple materials of degree one, the stresses in a material point result from the past values ​​and the current value of the Green-Lagrange strain tensor or values ​​derived therefrom at this point. Materials of a higher degree also use higher derivatives according to the material coordinates than the first ones, which make up the deformation gradient.

Material constraints

Material constraints represent kinematic constraints that limit the deformation possibilities of a material. The best known of these conditions is incompressibility, which only allows the material to deform in terms of volume, as shown by some liquids or rubber-elastic materials . The kinematic secondary condition is here . The reaction stresses in the material no longer result from the constitutive equations, but from the balance equations and boundary conditions . With incompressibility z. B. the reaction voltage is the pressure in the material. The strongest secondary condition is that which characterizes the rigid body . All constitutive equations are omitted here and the stresses are completely determined by the laws of nature and boundary conditions. ${\displaystyle \det(\mathbf {F} )\equiv 1}$

Material symmetries

Material symmetries describe which transformations of the material are possible without the stresses changing with a given deformation gradient. These transformations form the symmetry group of the material. If all volume-preserving transformations are allowed, a liquid or a gas is present. Only rotations are possible with solids : with isotropic solids all rotations, with transversely isotropic any rotations around an axis, with cubic anisotropic only 90-degree rotations about three mutually orthogonal axes, with orthotropic only 180-degree rotations around three mutually orthogonal axes Axes and with completely anisotropic only "rotations" of 0 degrees are allowed.

Constitutive equations

The constitutive equations give a relation between the strains and the stresses in the form of integral, differential or algebraic equations. The following material models give examples of constitutive equations.

1. Ideal gas : With the ideal gas, the pressure is proportional to the density and temperature : the number is a material parameter. This material model, in conjunction with the continuity equation and the momentum balance, leads to the Euler equations . ${\displaystyle p}$ ${\displaystyle \rho }$ ${\displaystyle T}$
   ${\displaystyle {\boldsymbol {\sigma }}=-p\mathbf {1} =-RT\rho \mathbf {1} }$
   ${\displaystyle R}$
2. Linear viscous or Newtonian fluid : The material parameters and are the first and second Lamé constants and the trace . In connection with the continuity equation and the momentum balance, this material model provides the Navier-Stokes equations .
   ${\displaystyle {\boldsymbol {\sigma }}=-p(\rho )\mathbf {1} +2\mu \mathbf {d} +\lambda \operatorname {Sp} (\mathbf {d} )\mathbf {1} }$
   ${\displaystyle \lambda }$ ${\displaystyle \mu }$ ${\displaystyle \operatorname {Sp} }$
3. Hooke's law for linear elastic isotropic solids: . It is the modulus of shear , the Poisson's ratio . In connection with the momentum balance, this material model gives the Navier-Cauchy equations .
   ${\displaystyle {\boldsymbol {\sigma }}=2G\left({\boldsymbol {\varepsilon }}+{\frac {\nu }{1-2\nu }}\operatorname {Sp} ({\boldsymbol {\varepsilon }})\mathbf {1} \right)}$
   ${\displaystyle G}$ ${\displaystyle \nu }$
4. Viscoelasticity: . It means the derivative according to the time parameter , the deviator and and are relaxation functions for the shear or volumetric part of the deformation.
   ${\displaystyle {\boldsymbol {\sigma }}=2\int _{0}^{t}\gamma (t-\tau ){\boldsymbol {\varepsilon }}(\tau )'^{\mathrm {D} }\,\mathrm {d} \tau +\int _{0}^{t}\kappa (t-\tau )\operatorname {Sp} [{\boldsymbol {\varepsilon }}(\tau ){\text{'}}]\,\mathrm {d} \tau \mathbf {I} }$
   ${\displaystyle (\cdot )'}$ ${\displaystyle \tau }$ ${\displaystyle (\cdot )^{\mathrm {D} }}$ ${\displaystyle \gamma (t)}$ ${\displaystyle \kappa (t)}$
5. Plasticity : With velocity-independent plasticity, the material behavior is described with algebraic and differential equations. The algebraic equations determine the additive splitting of the strains into an elastic and a plastic part, the relationship between the stresses and the elastic strains and the flow area that separates the elastic area from the plastic area in the stress space. With differential equations the development of the inner variables, e.g. B. the plastic strain described. In classical plasticity, the stresses remain on the flow surface during flow.
6. Viscoplasticity: With speed-dependent plasticity, the material behavior is also represented with algebraic and differential equations. Here, however, the stresses can temporarily lie outside the yield surface, but return to it during relaxation .

The solid models three to six are representatives of the four groups of models of classical material theory, which describe speed-dependent or independent behavior with or without (equilibrium) hysteresis .

example

Rotation with uniaxial deformation. The initial configuration is shown in gray, the current configuration in green.

Based on the expansion of a twisted block under pure tension (see picture), the equations of continuum mechanics are to be applied. In the initial configuration in the global Cartesian coordinate system, it has the length in the x direction, the width in the y direction and the height in the z direction and is aligned at the origin parallel to the coordinate axes. This block is elongated, stretching in the material X, Y or Z direction, and then rotated by 90 ° around the z axis. ${\displaystyle L}$ ${\displaystyle B}$ ${\displaystyle H}$ ${\displaystyle \lambda ,\beta ,\eta }$

In the current configuration, the material points have

${\displaystyle {\vec {X}}=(X,Y,Z)^{\top }\in [0,L]\times [0,B]\times [0,H]}$

then the spatial coordinates

${\displaystyle {\vec {\chi }}({\vec {X}},t)={\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}-\beta Y\\\lambda X\\\eta Z\end{pmatrix}}\,.}$

The material lines with and are aligned parallel to the y-axis in the current configuration. In the current configuration, a move in the material x-direction corresponds to a move in the spatial y-direction. ${\displaystyle X\in [0,L]}$ ${\displaystyle Y,Z=\mathrm {const.} }$

The deformation and displacement gradients are calculated from the derivation

${\displaystyle \mathbf {F} =\sum _{i,j=1}^{3}{\frac {\mathrm {d} \chi _{i}}{\mathrm {d} X_{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}={\begin{pmatrix}0&-\beta &0\\\lambda &0&0\\0&0&\eta \end{pmatrix}}\Rightarrow \mathbf {H} ={\begin{pmatrix}-1&-\beta &0\\\lambda &-1&0\\0&0&\eta -1\end{pmatrix}}\,.}$

The polar decomposition results from the 90 ° rotation

${\displaystyle {\begin{array}{l}\mathbf {F} ={\begin{pmatrix}0&-\beta &0\\\lambda &0&0\\0&0&\eta \end{pmatrix}}={\begin{pmatrix}0&-1&0\\1&0&0\\0&0&1\end{pmatrix}}{\begin{pmatrix}\lambda &0&0\\0&\beta &0\\0&0&\eta \end{pmatrix}}={\begin{pmatrix}\beta &0&0\\0&\lambda &0\\0&0&\eta \end{pmatrix}}{\begin{pmatrix}0&-1&0\\1&0&0\\0&0&1\end{pmatrix}}\\\Rightarrow \mathbf {R} ={\begin{pmatrix}0&-1&0\\1&0&0\\0&0&1\end{pmatrix}},\mathbf {U} ={\begin{pmatrix}\lambda &0&0\\0&\beta &0\\0&0&\eta \end{pmatrix}},\mathbf {V} ={\begin{pmatrix}\beta &0&0\\0&\lambda &0\\0&0&\eta \end{pmatrix}}\end{array}}\,.}$

From this we get the strain tensors:

${\displaystyle {\begin{array}{l}\mathbf {E} ={\frac {1}{2}}{\begin{pmatrix}\lambda ^{2}-1&0&0\\0&{\beta }^{2}-1&0\\0&0&{\eta }^{2}-1\end{pmatrix}},\mathbf {e} ={\frac {1}{2}}{\begin{pmatrix}1-{\beta }^{-2}&0&0\\0&1-\lambda ^{-2}&0\\0&0&1-{\eta }^{-2}\end{pmatrix}},\\{\mathbf {E} }_{N}={\begin{pmatrix}\lambda -1&0&0\\0&\beta -1&0\\0&0&\eta -1\end{pmatrix}},\mathbf {E} _{H}={\begin{pmatrix}\ln(\lambda )&0&0\\0&\ln(\beta )&0\\0&0&\ln(\eta )\end{pmatrix}}\\{\boldsymbol {\varepsilon }}={\frac {1}{2}}{\begin{pmatrix}-2&\lambda -\beta &0\\\lambda -\beta &-2&0\\0&0&2\eta -2\end{pmatrix}}\end{array}}}$

from which you can see that with large rotations the geometrically linear expansions cannot be used. ${\displaystyle {\boldsymbol {\varepsilon }}}$

Using Hooke's law for large deformations, the second Piola Kirchhoff stresses in the Lagrange image result:

${\displaystyle {\tilde {\mathbf {T} }}=2G\left[\mathbf {E} +{\frac {\nu }{1-2\nu }}\operatorname {Sp} (\mathbf {E} )\mathbf {1} \right]=2G\left[{\frac {1}{2}}{\begin{pmatrix}\lambda ^{2}-1&0&0\\0&{\beta }^{2}-1&0\\0&0&{\eta }^{2}-1\end{pmatrix}}+{\frac {\nu (\lambda ^{2}+\beta ^{2}+\eta ^{2}-3)}{2(1-2\nu )}}{\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}\right]\,.}$

With pure pull in the material x-direction by means of one recognizes and therefore ${\displaystyle {\tilde {\mathbf {T} }}={\tilde {T}}_{xx}{\vec {e}}_{x}\otimes {\vec {e}}_{x}}$ ${\displaystyle \beta =\eta }$

${\displaystyle {\frac {1}{2}}(\beta ^{2}-1)+{\frac {\nu (\lambda ^{2}+2\beta ^{2}-3)}{2(1-2\nu )}}=0\Rightarrow {\frac {\beta ^{2}-1}{2}}={\frac {\eta ^{2}-1}{2}}=-\nu {\frac {\lambda ^{2}-1}{2}}\Rightarrow {\tilde {T}}_{xx}=\mathrm {E} {\frac {\lambda ^{2}-1}{2}}\,,}$

where is the elastic modulus . The nominal stress tensor is ${\displaystyle \mathrm {E} =2G(1+\nu )}$

${\displaystyle \mathbf {N} ={\tilde {\mathbf {T} }}\cdot \mathbf {F} ^{\top }={\begin{pmatrix}{\tilde {T}}_{xx}&0&0\\0&0&0\\0&0&0\end{pmatrix}}\cdot {\begin{pmatrix}0&\lambda &0\\-\beta &0&0\\0&0&\eta \end{pmatrix}}={\begin{pmatrix}0&N_{xy}&0\\0&0&0\\0&0&0\end{pmatrix}}}$ With ${\displaystyle N_{xy}=\mathrm {E} \lambda {\frac {\lambda ^{2}-1}{2}}\,.}$

In the statics considered here, the law of momentum states

${\displaystyle {\vec {0}}=\operatorname {DIV} \;\mathbf {N} ={\frac {\partial }{\partial X}}N_{xy}{\vec {e}}_{y}\,,}$

what is given because of . The Cauchy stress tensor is given the form: ${\displaystyle \lambda =\mathrm {const.} }$

${\displaystyle {\boldsymbol {\sigma }}={\frac {\mathbf {F\cdot N} }{\det(\mathbf {F} )}}={\frac {1}{\lambda \beta \eta }}{\begin{pmatrix}0&-\beta &0\\\lambda &0&0\\0&0&\eta \end{pmatrix}}\cdot {\begin{pmatrix}0&N_{xy}&0\\0&0&0\\0&0&0\end{pmatrix}}=\mathrm {E} {\frac {\lambda (\lambda ^{2}-1)}{2(1+\nu -\nu \lambda ^{2})}}{\vec {e}}_{y}\otimes {\vec {e}}_{y}\,.}$

If the block is compressed to zero length so that it is, these tensions disappear. This shows that Hooke's law is not applicable to such large deformations. Hooke's law only gives physically plausible answers for moderate elongations. ${\displaystyle \lambda =0}$

The unit cube is suitable as a reference configuration ${\displaystyle {\vec {\Theta }}=\kappa _{R}(P)}$

${\displaystyle (\Theta _{1},\Theta _{2},\Theta _{3})\in {[-1,1]}^{3}\subset \mathbb {V} ^{3}\,.}$

This is how the material points get their coordinates in the initial configuration ${\displaystyle {\vec {X}}=\kappa _{0}(\kappa _{R}^{-1}({\vec {\Theta }}))=:{\vec {\chi }}_{0}({\vec {\Theta }})}$

${\displaystyle X={\tfrac {1}{2}}L(\Theta _{1}+1),\quad Y={\tfrac {1}{2}}B(\Theta _{2}+1),\quad Z={\tfrac {1}{2}}H(\Theta _{3}+1)\,.}$

The "deformation gradient" operating between the reference and the initial configuration is also referred to as the Jacobi matrix :

${\displaystyle \mathbf {J} ({\vec {\Theta }})=\sum _{i,j=1}^{3}{\frac {\mathrm {d} \chi _{0i}}{\mathrm {d} \Theta _{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}={\frac {1}{2}}{\begin{pmatrix}L&0&0\\0&B&0\\0&0&H\end{pmatrix}}\quad \rightarrow \quad \det(\mathbf {J} )={\frac {LBH}{8}}\,.}$

The volume integral of a field size is then ${\displaystyle \phi }$

${\displaystyle \int _{V}\phi ({\vec {X}},t)\mathrm {d} V=\int _{-1}^{1}\int _{-1}^{1}\int _{-1}^{1}\phi (\chi _{0}({\vec {\Theta }}),t)\det(\mathbf {J} ({\vec {\Theta }}))\,\mathrm {d} \Theta _{1}\,\mathrm {d} \Theta _{2}\,\mathrm {d} \Theta _{3}}$

and in this form can be calculated numerically with the Gaussian quadrature .

See also

• Technical mechanics , rheology
• Cauchy elasticity , hyperelasticity , hypoelasticity
• Orthotropy , transverse isotropy , cubic anisotropy
• Main invariant
• Stress function , Airy stress function
• Compatibility condition
• Orthogonal tensor , deviator , spherical tensor

Footnotes

1. ↑ H. Altenbach, p. 3 ff
2. ↑ F. Durst, p. 10 ff
3. ↑ In the literature, another definition is used, which differs from the one used here only through the transposition of the tensor. The formulas usually only receive minor modifications in the formulation and can be converted straight into one another.
4. ↑ The transposition of the stress tensor ensures that the first index in its components points to the normal of the cut surface and the second index indicates the direction of action. ${\displaystyle \sigma _{ij}}$

literature

• H. Altenbach: Continuum Mechanics . Springer Verlag, 2012, ISBN 978-3-642-24118-5 .
• H. Parisch: Solid Continuum Mechanics . Teubner, 2003, ISBN 3-519-00434-8 .
• A. Bertram: Axiomatic introduction to continuum mechanics. Wissenschaftsverlag, 1989, ISBN 3-411-14031-3 .
• Ernst Becker & Wolfgang Bürger: Continuum Mechanics. Teubner, 1975, 228 pp., ISBN 3-519-02319-9 .
• F. Durst: Fundamentals of Fluid Mechanics. Springer Verlag, 2006, ISBN 3-540-31323-0 .
• Ralf Greve: Continuum Mechanics. Springer Verlag, 2003, ISBN 3-540-00760-1 .
• Peter Haupt: Continuum Mechanics and Theory of Materials. Springer, Berlin et al. 2000, ISBN 3-540-66114-X .
• Wolfgang H. Müller: Forays through the continuum theory. Springer Verlag, 2011, ISBN 3-642-19869-4
• Valentin L. Popov: Contact Mechanics and Friction. A text and application book from nanotribology to numerical simulation. Springer Verlag, 2009, ISBN 978-3-540-88836-9 .
• Arnold Sommerfeld: Mechanics of deformable media. (= Lectures on theoretical physics , volume 2). Becker & Erler, Leipzig 1945. (6th edition, Harri Deutsch, Thun 1992, ISBN 3-87144-375-1 .)
• C. Truesdell, W. Noll: The non-linear field theories of mechanics. Springer Verlag, 1992, ISBN 3-540-55098-4 .

Web links

Wiktionary: Continuum mechanics  - explanations of meanings, word origins, synonyms, translations

• Online lecture on continuum physics by Krishna Garikipati, University of Michigan (English)