Mathematics in the heyday of Islam

A page from al-Khwarizmi's book Hisab al-Jabr wa-l-muqabala

The mathematics in the Islamic Golden Age was based on the findings of the ancient Greek and Indian mathematics , they added in the period between the 8th and 13th centuries as well as many new features and enhancements added. While at the same time the works of antiquity were almost forgotten in early medieval Christian Europe and hardly any scientific progress worth mentioning was made there, scholars in the Islamic world preserved the continuity of mathematical research. For this reason they play an important role in the history of mathematics . Important mathematicians in the heyday of Islam were for example al-Chwarizmi , Thabit ibn Qurra , al-Battani , Abu l-Wafa , Alhazen and Omar Chayyam .

In the field of arithmetic , the Islamic mathematicians took over the decimal notation from Indian mathematics , expanded it to include decimal fractions and developed procedures for efficient written arithmetic in this number representation. In doing so, they contributed significantly to the spread of the decimal place value system used today . The most important innovation in the mathematics of the Islamic countries was the development of algebra up to the systematic transformation and solving of equations as well as calculation with root terms , powers and polynomials . In trigonometry , too, based on the sine function adopted from India , great progress has been made in the investigation of plane and spherical triangles through the definition of the other trigonometric functions . Islamic mathematics also made contributions to constructions of Euclidean geometry, as well as number theory and combinatorics .

term

In the countries of Islam, especially under the rule of the Abbasids from the 8th to the 13th century, there was a cultural and scientific upswing in literature and philosophy, architecture, medicine, astronomy, geography and, last but not least, mathematics a heyday. There is no standard short name in the literature for this section of the history of mathematics . Until recently, “Arabic mathematics” was often used, which is justified by the fact that the writings of this era were almost exclusively written in Arabic . However, the term can be misleading because it also refers to Arabs as an ethnic group, whereas the scholars of the time came from different parts of the Islamic world. Today's texts therefore mostly refer to Islam as the common cultural background and use terms such as "Mathematics in the countries of Islam" or "Mathematics of Islam" and "Islamic mathematics" for short. With terms derived from this, such as “Islamic mathematician” or “mathematician of Islam”, however, it should be noted that no statement is made about the person's religious affiliation. Most of the scholars in the countries of Islam were Muslims , but not all of them. A well-known example is the mathematician as-Samaw'al consisting of a Jewish native family and only after the publication of his major works to the Islamic faith converted .

Historical and social background

Spread of Islam up to 750:

under Mohammed, 612-632

among the first three caliphs, 632–655

under the Umayyad Caliphate 661–750

The Islamic calendar begins in AD 622 with the hijra , the flight of the founder of religion Mohammed from his hometown of Mecca to Medina . By his death in 632, the new monotheistic religion of Islam had already spread across the entire Arabian Peninsula . Mohammed's successors, the caliphs , set up powerful armies as religious and political leaders and were able to quickly expand the Islamic sphere of influence through the conquest of Syria, Mesopotamia , Persia and Egypt by the middle of the 7th century. Under the Umayyad Caliphate , the triumphal march of the Islamic armies continued: in the west across North Africa ( Maghreb ) to the Iberian Peninsula ( al-Andalus ) and in the east to Central Asia ( Turkestan ) and India as far as the Indus ( Sindh ).

The Abbasid caliph al-Ma'mun (far left) and the Byzantine emperor Theophilos (far right), in front of them as mediating envoy Johannes Grammatikos ; Detail from the Madrid illuminated manuscript of the Skylitz

Around the year 750 the expansion of Islam had essentially come to a standstill and a phase of consolidation began in the new empire. Al-Mansur , the second Abbasid caliph , relocated the capital from Damascus to Baghdad , which was built from 762 onwards and which subsequently became a center of culture and science. Harun ar-Raschid founded a library there, in which numerous scientific sources from all parts of the empire were collected. Ar-Raschid's son, the Caliph al-Ma'mun (reign 813-833), had the " House of Wisdom " (Bayt al-Hikma) built in Baghdad . The main task of this scientific institution, which was also an academy, library and translation workshop, was initially to translate the most important scientific sources into the Arabic language . As the language of the Koran that everyone in the Islamic empire had to learn, Arabic played a central role as the lingua franca for trade, culture and science. Arabic translations of Indian sources had already been made in the east of the empire in the 730s. Thanks to the work in the House of Wisdom, by the end of the 9th century the most important Greek mathematical works were also available in careful translation - above all the elements of Euclid , but also the mathematical treatises of Archimedes , the Konika (“On the Conic sections ”) by Apollonios , the Arithmetica by Diophant and the Sphaerica by Menelaus . In addition, the translation work in the House of Wisdom also creatively shaped the Arabic scientific terminology as the basis for further scientific progress.

Progress in the sub-areas

arithmetic

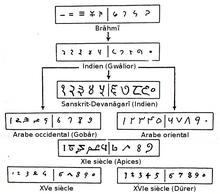
Adoption and distribution of the Indian decimal system

The development of the Indo-Arabic numerals

The essential element of the decimal place value representation of numbers is a symbol for the zero , which indicates that the corresponding step number does not appear at this point : Thus the number 207 contains twice 100, never 10 and seven times 1; in contrast to 27, which contains 10 twice and 1 seven times. This important idea of ​​zero goes back to Indian mathematics, where it was used at least since the 7th century AD and was described by the Indian astronomer and mathematician Brahmagupta . The Indian numerals spread to Syria and Mesopotamia by the 8th century and were adopted by Islamic mathematics in the 9th century. Previously, the Arabs used the Abdschad number script , in which, similar to the Greek number script, the letters of the alphabet stand for certain numerical values. With the Arabic translation of the Siddhānta by the Indian mathematician Aryabhata in the 8th century, the number zero found its way into Arabic-language literature. The zero was called sifr (“empty”, “nothing”) in Arabic ; The German word “number” and the English “zero” for zero developed from this designation.

The first known description of this new number system in Arabic comes from the polymath al-Khwarizmi , one of the most important mathematicians of Islam. He was probably of Khorezmian descent, was born around 780, worked in the House of Wisdom in Baghdad and died between 835 and 850. His work kitāb al-ḥisāb al-hindī (Book of calculating with Indian numbers) or kitab al-jam 'wa' l-tafriq al-ḥisāb al-hindī ('addition and subtraction in Indian arithmetic'), translated into Latin in the 12th century, introduced the Indo-Arabic numbers and the decimal system in Europe. The work has only survived in a single Latin manuscript; the Arabic original has been lost. The Latin translation begins with the words: "Dixit algorizmi" ("Al-Chwarizmi said"). The word " algorithm " , which is used today for systematic calculation processes, developed from this . Contrary to its title, al-Khwarizmi's introduction to the Indian number system contained not only procedures for adding and subtracting in writing , but also for multiplying , dividing and extracting square roots . One of the earliest surviving works on arithmetic in the original Arabic text, the book Fundamentals of Indian Arithmetic by Kuschyar ibn Labban (fl. 971-1029), was very influential in Islamic countries and played an important role in the final spread of the decimal system.

Addition of 5625 and 839 on a dust table according to Kuschyar ibn Labban

The written arithmetic techniques introduced by al-Chwarizmi and Kuschyar ibn Labban differed significantly from those used today. The reason for this was that they were optimized for calculating on a so-called dust table , a flat tray sprinkled with fine sand, which was common at that time . In contrast to calculating with pen and paper, only a relatively small number of digits could be written on a dust board at the same time, but it had the advantage that digits could be erased very quickly and overwritten by others. However, dust tables as a calculation tool soon fell out of use in favor of ink and paper. For example, Abu l-Hasan al-Uqlidisi wrote in his book of chapters on Indian arithmetic , written around 953 , that the use of the dust table is “not appropriate”, because otherwise it is only seen in “ good-for-nothing ” people who “are in the streets make a living from astrology ”. Accordingly, al-Uqlidisi stated in his book written calculation techniques that were optimized for the cover letter on paper.

Invention of the decimal fractions

In al-Uqlidisi's book on Indian arithmetic, in addition to calculating with natural numbers in decimal notation, there is also the oldest known treatment of decimal fractions . Previously it was customary to use fractional parts in the sexagesimal system . Al-Uqlidisi introduced decimal fractions in connection with divisions by 2 and by 10 and demonstrated the usefulness of this new form of representation with examples: He halved the number 19 five times and got 0.59375 or increased the number 135 five times by a tenth, which is a decimal fraction 217.41885 results. Al-Uqlidisi did not yet use today's spelling with a decimal separator , but instead marked the units position by putting a small vertical line above it.

The use of decimal fractions in al-Uqlidisi still appeared largely as a technical device and arithmetic aid; it is unclear whether he fully recognized its mathematical significance. The full mathematical understanding of decimal fractions for the approximate representation of real numbers, however, can only be found more than 200 years later in a treatise on arithmetic by as-Samaw'al (around 1130 to around 1180) from the year 1172. As-Samaw'al led her there carefully as a method to approximate numbers with (in principle) arbitrary precision, and demonstrated this with examples by determining, among other things, decimal fraction expansions from and from . As-Samaw'al also used numerical iteration methods to calculate higher roots, in which the idea of ​​the “convergence” of the calculated approximations against the value sought becomes clear. The last great mathematician in the countries of Islam during the European Middle Ages, Jamschid Masʿud al-Kaschi (around 1389 to 1429), wrote the work Key to Arithmetic in 1427 , in which, based on the binomial theorem , he developed a general method for calculating nth roots described. ${\displaystyle {\tfrac {210}{13}}}$ ${\displaystyle {\sqrt {10}}}$

algebra

The algebra as an independent mathematical branch has been developed by mathematicians in the Islamic Golden Age. Important sources from which they drew from and which they combined to form a new science were Greek mathematics, especially the elements of Euclid and the Arithmetica of Diophant , and Indian mathematics, especially the work Brahmasphutasiddhanta by Brahmagupta from the 7th century . Islamic mathematics combined the more geometrical and always carefully proven approach of the Greeks with the practically arithmetic solving of equations handed down from India, as was already used in Babylonian mathematics .

The Banū-Mūsā brothers, who worked at the same time as al-Khwarizmi in Baghdad in the 9th century, were among the first Arabic-speaking mathematicians to develop ancient mathematics independently and creatively . They described a solution similar to “ Pascal's snail ” for dividing the angle into three and calculating the cube root from a non- cubic number in sexagesimal fractions . They performed a circle calculation using Archimedes' method, and they knew Heron's theorem.

The Islamic mathematicians did not yet use mathematical symbols to specify, transform and solve equations, but instead expressed them exclusively in words, possibly supplemented by geometric figures. Although they used the number zero , as shown above , they did not use the number zero, nor did they adopt the concept of negative numbers, as was previously in use in India and China.

An important application of algebra was the sharing of property in Islamic inheritance law, which with its relatively complicated legal provisions naturally leads to mathematical equations. Correspondingly, the treatises of the Islamic mathematicians often also contained application exercises on this topic.

Algebraic transformations and solutions of equations in al-Chwarizmi

In addition to his introduction to arithmetic, Al-Chwarizmi wrote another mathematical work that is considered the starting point of algebra as an independent science. It bears the title al-Kitab al-muchtasar fi hisab al-dschabr wa-l-muqabala (for example: "The concise book on the computational methods by supplementing and balancing"). The work was translated into Latin by Robert von Chester in 1145 under the title Liber algebrae et almucabala . The first part shows the systematic transformation and solving of quadratic equations ; in the second part there are numerous application tasks that illustrate the process. Al-Chwarizmi first explained how every solvable quadratic equation was carried out using two transformation techniques, which he called al-dschabr ("supplement"; later the word "algebra") and al-muqabala ("balance"), to one of six Standard forms can be brought. In modern notation with the unknown and with coefficients and , which denote given positive numbers, these are: ${\displaystyle x}$ ${\displaystyle p}$ ${\displaystyle q}$

1) , ${\displaystyle x^{2}=px}$	2) , ${\displaystyle x^{2}=p}$	3) , ${\displaystyle x=p}$
4) , ${\displaystyle x^{2}+px=q}$	5) , ${\displaystyle x^{2}+q=px}$	6) . ${\displaystyle px+q=x^{2}}$

Two cases of quadratic equations in al-Khwarizmi (Arabic copy from the 14th century)

In the first three cases, the solution can be determined directly; for cases 4, 5 and 6, al-Chwarizmi gave rules for the solution and proved them geometrically by completing the square . He always used concrete numerical examples, but emphasized the general validity of the considerations.

The procedure is to be explained in the example of case 5, in which al-Chwarizmi established that it is the only one of the six cases in which no, exactly one or exactly two (positive) solutions can exist. All other cases, however, always have a clearly defined solution. The equation is given . This is first transformed by al-dschabr , which means that terms that are subtracted (in this case ) are added on both sides of the equation, so that ultimately only additions occur in the equation; in the example it results . The second transformation step, al-muqabala , is to combine terms of the same type on the left and right of the equation on one side; in the example one obtains . Division of the equation by 2 finally yields the normal form . With the rule given by al-Chwarizmi for case 5, the two solutions can now be determined: ${\displaystyle 2x^{2}+100-20x=58}$ ${\displaystyle 20x}$ ${\displaystyle 2x^{2}+100=58+20x}$ ${\displaystyle 2x^{2}+42=20x}$ ${\displaystyle x^{2}+21=10x}$

${\displaystyle {\frac {10}{2}}-{\sqrt {\left({\frac {10}{2}}\right)^{2}-21}}=3\quad }$and . ${\displaystyle \quad {\frac {10}{2}}+{\sqrt {\left({\frac {10}{2}}\right)^{2}-21}}=7}$

Further development of algebra in Islam

The ideas that al-Khwarizmi presented in his book on al-Jabr and al-muqabala were taken up, commented on and deepened by many Islamic mathematicians. Thabit ibn Qurra (826-901) wrote a treatise in which he generally proved the solution formulas shown by al-Chwarizmi using special numerical examples. For this he used two theorems from Euclid's elements and showed that the geometric solutions thus proved correspond to the formulas obtained by algebraic transformations.

Probably from Egypt, the scholar Abu Kamil (around 850 to around 930) published a very influential book called Algebra . The collection of exercises contained therein was intensively taken up , for example, towards the end of the 12th century by the Italian mathematician Leonardo von Pisa . Abu Kamil's algebra , intended as a commentary on al-Khwarizmi's work, contains numerous advances in algebraic transformations. Among other things, he showed calculation rules for multiplying expressions that contain the unknown, or calculation rules for roots, such as . In doing so, he carried out careful evidence for elementary transformations such as . The second part of Abu Kamil's algebra contains numerous exercises that illustrate the theoretical first part. One of the problems is interessantesten loud John Lennart Berggren his "virtuoso" dealing with the rules of algebra: Abu Kamil looked in the non-linear system of equations , , with three unknowns and gave detail the calculation steps, which finally on the solution lead. ${\displaystyle {\sqrt {a}}\cdot {\sqrt {b}}={\sqrt {a\cdot b}}}$ ${\displaystyle ax\cdot bx=ab\cdot x^{2}}$ ${\displaystyle 10=x+y+z}$ ${\displaystyle z^{2}=x^{2}+y^{2}}$ ${\displaystyle xz=y^{2}}$ ${\displaystyle x=5-{\sqrt {{\sqrt {3125}}-50}}}$

In the following years there was a further arithmetization of algebra, that is, its geometric origins faded into the background and the purely algebraic laws of calculation were further developed. The Persian mathematician al-Karaji (953-1029) considered arbitrary powers of the unknowns as well as sums and differences formed from them. With this he took an important step in the direction of arithmetic for polynomials , but failed because of a generally valid formulation of the polynomial division because he - like all Islamic mathematicians before him - lacked the concept of negative numbers. It was not until as-Samaw'al , about 70 years later, that the power law for any positive and negative exponents and was found . As-Samaw'al was able to provide an efficient tabular procedure with which any polynomial divisions can be carried out; for example he calculated with it ${\displaystyle x}$ ${\displaystyle x^{m}\cdot x^{n}=x^{m+n}}$ ${\displaystyle m}$ ${\displaystyle n}$

${\displaystyle {\frac {20x^{6}+2x^{5}+58x^{4}+75x^{3}+125x^{2}+96x+94+140x^{-1}+50x^{-2}+90x^{-3}+20x^{-4}}{2x^{3}+5x+5+10x^{-1}}}}$.

A page from Omar Chayyam's paper on solving cubic equations using conics

In the field of solving algebraic equations, the Persian scientist and poet Omar Chayyam (1048–1131) took up al-Chwarizmi's classification of quadratic equations and expanded it to cubic equations , i.e. equations that contain the third power of the unknown. He showed that these can be reduced to one of 25 standard forms, 11 of which can be reduced to quadratic equations. For the other 14 types, Omar Chayyam specified methods with which the solutions can be constructed geometrically as intersections of conic sections . In his treatise, he also expressed the “wish” to be able to calculate the solution algebraically using root expressions, as with the quadratic equations also with the cubic equations. However, according to Omar Chayyam, neither he nor any other algebraic was successful. Chayyam's wish was not fulfilled until 1545 with the publication of formulas for solving equations of the third degree by the Italian scholar Gerolamo Cardano .

trigonometry

Trigonometric functions

The origins and the first applications of trigonometry , the "triangular measurement", in antiquity lay in astronomy . Mathematical texts that dealt with this area were therefore mostly individual sections in astronomical works. The Almagest by Ptolemaios (around 100 AD to after 160) contains the most comprehensive compilation of all the astronomical knowledge of ancient Greece that had been collected up to that point . The only "angle function" used by the Greek astronomers was the chord length associated with an angle (or arc ) . Correspondingly, a detailed tendon table is given in the Almagest, i.e. a table that contains angles in degrees in one column and the associated chord lengths in the other column. ${\displaystyle \alpha }$ ${\displaystyle \operatorname {chord} (\alpha )}$

However, the Islamic astronomers and mathematicians did not adopt the chordal geometry of the Greeks, but a different approach that was used in Indian astronomy : the sine geometry. In a right-angled triangle is the ratio of the length of the angle opposite cathetus to the length of the hypotenuse . Although there is a relatively simple relationship between the sine and the arc length , the direct relationship of the sine to right triangles offers great theoretical and practical advantages. Sine tables had been in use in India since the 4th or 5th century . ${\displaystyle \sin(\alpha )}$ ${\displaystyle \alpha }$ ${\displaystyle \sin(\alpha )={\tfrac {1}{2}}\operatorname {chord} (2\alpha )}$

The extension of the sine function to the six trigonometric functions used today sine, cosine, tangent , cotangent, secant and cosecant is an innovation in Islamic mathematics. Tangent and cotangent were first introduced in connection with shadow lengths: If the elevation angle of the sun is above the horizon, then is the shadow length that a horizontal rod of length 1 casts on a vertical wall; a stick ( gnomon ) standing vertically on the ground casts a shadow of length . Secans and cosecans then correspond to the hypotenuses belonging to the shadow, i.e. they are equal to the distance between the tip of the gnomon and that of the shadow. Because of the simple relationships , and it is sufficient for the practice to set up tables for sine, tangent and secant. ${\displaystyle \theta }$ ${\displaystyle \tan(\theta )}$ ${\displaystyle \cot(\theta )}$ ${\displaystyle \cos(\theta )=\sin(90^{\circ }-\theta )}$ ${\displaystyle \cot(\theta )=\tan(90^{\circ }-\theta )}$ ${\displaystyle \csc(\theta )=\sec(90^{\circ }-\theta )}$

The efficiency of these new concepts was shown for the first time with Abu l-Wafa , who developed the addition theorem of the sine in the 10th century

${\displaystyle \sin(\alpha \pm \beta )=\sin(\alpha )\cdot \cos(\beta )\pm \cos(\alpha )\cdot \sin(\beta )}$

formulated and proven in its modern form. This relationship represented a simplification in comparison to the analogous statement for chord lengths known up to now. An extremely important theorem of trigonometry, the sine theorem for plane triangles, was first proven by the Persian scholar Nasir ad-Din at-Tusi in the 13th century. For the first time, it was possible to calculate any triangle from three details about its angles or sides.

Spherical trigonometry

Three points A, B, C on a sphere form a spherical triangle with sides a, b, c and angles α, β and γ.

As in ancient Greece and India, spherical trigonometry was closely related to questions of astronomy in Islamic mathematics: Astronomical objects can be understood as points on the celestial sphere . The shortest connection between two points on this sphere is an arc of a great circle , three points together with the great circle arcs that connect them form a spherical triangle . The only general mathematical way of calculating the length of the sides of spherical triangles and squares known to the Greeks was based on an application of Menelaus' theorem . It is named after Menelaus of Alexandria , who lived a few decades before Ptolemy and, as far as is known, was the first scholar to study spherical triangles. In the case of problems in which this theorem was impossible or difficult to apply, practical measurement and approximation methods were otherwise used in astronomy, such as spherical models or astrolabes , the functioning of which is based on the fact that the celestial sphere is mapped onto a plane through stereographic projection .

An important advance in Islamic mathematics, which significantly simplified calculations compared to Menelaus' theorem, was the sine law for spherical triangles . It was formulated and proven by Abu al-Wafa and, presumably independently thereof, by al-Biruni and one of his teachers. This was the first time that a possibility was available to directly calculate angles (and not just sides) of spherical triangles. The theorem states: In a spherical triangle with angles , , and the lengths , , the respective opposite sides of the following applies: ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

${\displaystyle {\frac {\sin a}{\sin \alpha }}={\frac {\sin b}{\sin \beta }}={\frac {\sin c}{\sin \gamma }}}$.

In particular, a spherical triangle can be calculated from three given quantities if one side and an opposite angle are given.

Spherical triangle to determine the direction of prayer

The spherical trigonometry is of great importance not only in astronomy, but also in geography , when the spherical shape of the earth is taken into account in measurements and calculations . Al-Biruni has an important application for the Islamic religion: the determination of the Qibla , the direction of prayer to Mecca . Al-Biruni addressed this problem in a paper on mathematical geography entitled Determining the Coordinates of Cities . In it he assumed that the longitude and latitude of a city and the longitude and latitude of Mecca are given. In the spherical triangle with the North Pole , the two sides and and their intermediate angles are known at. Since the side opposite the given angle is unknown, the sine law cannot be applied directly. This problem would be solved today, for example, with the cosine theorem , which al-Biruni was not yet available. Instead, he used auxiliary triangles and multiple applications of the law of sines to calculate the angle in the point , i.e. the qibla . ${\displaystyle \mathrm {B} }$ ${\displaystyle \mathrm {A} }$ ${\displaystyle \mathrm {BAP} }$ ${\displaystyle \mathrm {P} }$ ${\displaystyle \mathrm {PA} }$ ${\displaystyle \mathrm {PB} }$ ${\displaystyle \mathrm {P} }$ ${\displaystyle \mathrm {B} }$

Euclidean geometry

The elements in which the Greek mathematician Euclid around 300 BC BC had systematically summarized the geometry of his time, were available in Arabic translation in the late 8th century and had a very great influence on the Islamic mathematicians. But also the treatise On Sphere and Cylinder by Archimedes and Apollonios' work Konika on conic sections were pillars on which geometry was based in Islamic countries. A popular subject of research was the construction of regular polygons with compasses and rulers . For regular triangles, squares, pentagons and fifteenagons and the regular polygons resulting from this by doubling the sides, construction was only known with compasses and rulers; on the other hand, regular heptagons and hexagons can only be constructed by using additional tools. Abu l-Wafa stated in his work About those parts of the geometry that craftsmen need, among other things, different constructions of these two cases with the help of conic sections or by so-called insertion (neusis) .

Another important mathematician who systematically dealt with geometric constructions was Abu Sahl al-Quhi (around 940 to around 1000). In particular, he wrote a treatise on the “perfect compass”, an instrument with which conic sections can be drawn. In addition to theoretical considerations for the construction of geometric figures, conic sections were also of great importance for practical applications such as sundials or burning mirrors. Ibrahim ibn Sinan (908-946), a grandson of Thabit ibn Qurra, gave in his work on drawing the three conic sections various methods for the construction of the three conic section types ellipse, parabola and hyperbola. Of theoretical and practical interest in Islamic mathematics were geometrical constructions that result from the restriction of the classical Euclidean tools. For example, Abu l-Wafa wrote a work that dealt with constructions with a ruler and a compass with a fixed opening, also known as "rusty compasses". In it he showed, for example, how one can use these tools to divide a segment into any number of equal sections or how to construct squares and regular pentagons.

Euclid's axiom of parallels: If the sum α + β of the interior angles is less than 180 °, then the straight lines h and k intersect at a point S, which lies on the same side of g as the two angles.

A purely theoretical problem that several Islamic mathematicians dealt intensively with was the question of what role the postulate of parallels plays in the axiomatic structure of Euclidean geometry. In his elements, Euclid used the “modern” structure of a mathematical theory by proving theorems on the basis of definitions and axioms , i.e. statements that are assumed to be true without proof. The axiom of parallels played a special role in this, and because of its relative complexity, it was not considered obvious from the start. Accordingly, there were numerous attempts in ancient times to prove this statement with the aid of the other axioms. For example, Alhazen (around 965 to after 1040) tried to approach this problem by reformulating the concept of parallel straight lines. Omar Chayyam later expressed disapproval because he did not consider Alhazen's use of a "moving straight line" to be obvious, and himself formulated a new postulate which he substituted for the Euclidean one. In the 13th century, Nasir ad-Din at-Tusi took up the evidence attempts of his predecessors and added more to them. It has been known since the 19th century that the axiom of parallels is independent of the other axioms, i.e. that it cannot be proven. All attempts that had been made to this end since ancient times were therefore flawed or contained circular reasoning.

Combinatorics and Number Theory

The ancient Indian results in combinatorics were adopted by the Islamic mathematicians. There have also been individual developments in this area. Statements about numbers or about natural numbers in general can often be proven by the principle of complete induction . In the works of Islamic mathematicians, there are some considerations that contain all the important components of this method of proof. So al-Karaji showed the formula in connection with power sums

${\displaystyle \sum _{i=1}^{n}i^{3}=\left(\sum _{i=1}^{n}i\right)^{2}}$.

Although he carried out the induction step on the concrete example , his approach was independent of his choice for . In al-Karaji, and even more clearly in as-Samaw'al, there are considerations that are essential steps to a proof of the binomial theorem ${\displaystyle n=10}$ ${\displaystyle n}$

${\displaystyle (x+y)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}x^{n-k}y^{k}}$

Pascal's triangle for determining the binomial coefficients

contained by complete induction - even if the mathematical possibilities of expression of the time were not sufficient to even formulate such a general statement. Al-Karaji and al-Samaw'al used the Pascal triangle to calculate the binomial coefficients , long before Blaise Pascal . ${\displaystyle {\tbinom {n}{k}}}$

The mathematician Ibn Munim (died 1228) from al-Andalus made significant contributions to combinatorics. In his book Fiqh al-hisab (" Laws of Calculation ") he started from the task of determining the number of all possible words in the Arabic language with a maximum of 10 letters. He approached this rather demanding problem - among other things, when it comes to word formation, the rules of how consonants and vowels must follow one another have to be observed - through various individual problems. So he first determined the number of different colored tassels that are created when you choose different colors from possible colors . Using the relationships between the binomial coefficients (see also combination (combinatorics) ), he finally succeeded in recursively determining the number of possible words of fixed length from the numbers of shorter words. ${\displaystyle n}$ ${\displaystyle k}$

In addition to magic squares and figured numbers , Islamic number theory also dealt with perfect numbers and their generalization, the friendly numbers . Two numbers are called friends if each is equal to the sum of the real divisors of the other. Only one example, the pair 220 and 284, has been known since antiquity, but no general mathematical statement about friendly numbers. In the 9th century Thabit ibn Qurra was able to specify and prove a law of formation (see theorem of Thabit ibn Qurra ). With his help, al-Farisi found another pair in the late 13th century, namely 17,296 and 18,416.

Decline and aftermath

In the 9th and 10th centuries, natural sciences and philosophy in the Islamic cultural area had reached the peak of their development. At that time, independent universities, the madrasas , were established there, which initially imparted in-depth scientific knowledge to their students in addition to religious knowledge. In Christian Europe, by contrast, many works had been lost or forgotten since late antiquity . Mathematics and science education was at a low point in the European early Middle Ages .

From the 10th century, the setting of relevant changes in Islamic legal scholar to from the Hellenistic philosophy evolved, Neoplatonically influenced Islamic philosophy and derived from these ethical standards. Empirical research as a source of knowledge and the way to the establishment of ethical and religious norms was perceived as being in contrast to Islamic law or religious studies and was only considered to be the private employment of individual scholars. The majority of believers should be guided by the ethical principles of Sharia law . The conclusion of this development is the work of the eminent legal scholar and mystic al-Ghazālī (1058–1111), who rejected the philosophy of Ibn Sina and other Hellenistic Muslim scholars as theistic and incompatible with Islamic theology. Accordingly, the madrasas gradually shifted their focus to legal and theological training, while scientific research and, as a result, a mathematical science that went beyond elementary applied mathematics lost its previous rank. In addition, political events such as the Reconquista in the Islamic West, the immigration of the Seljuks in the East and the Mongol storm , which Baghdad also succumbed to in 1258 , contributed to the end of the heyday of Arabic-language science in the Islamic cultural area, and thus indirectly to the decline of scientific science operated mathematics. With the exception of the two important Persian polymaths Nasir ad-Din at-Tusi (1201–1274) and Jamschid Masʿud al-Kaschi (1380–1429), Islamic culture hardly produced influential mathematicians in the period that followed.

Statue al-Khwarizmis, Amirkabir University ( Tehran )

At the time of the decline of the exact sciences in the countries of Islam, mathematical research had already taken off again in high and late medieval Europe. In the course of the reconquest of Spain and Sicily, the libraries of previously Islamic cities became freely accessible to Western European scholars; the ancient texts preserved there in Arabic translation, as well as the works of Arabic-speaking scholars, were translated into Latin . In Toledo , which was conquered in 1085, there was a lively activity of translating Arabic scripts . In this way, Western Europe gained access to the classical works of ancient mathematics for the first time via the Arabic language, above all to Euclid's Elements , which for a long time remained the most important mathematical work of all. But also the writings on the decimal system and on algebra, which from the beginning were regarded as achievements of Islamic mathematics, have been translated repeatedly and commented on again and again. The arithmetic and algebra of al-Chwarizmis, but also Abu Kamil's work, were taken up by Leonardo von Pisa and continued in his main work Liber abbaci . As-Samaw'al's advanced considerations on algebra or Omar Chayyam's mathematical research were unknown during the Renaissance and had to be reworked. It is unclear whether the advances in combinatorics, such as Pascal's triangle of binomial coefficients, were adopted from Islamic mathematics or whether they were developed independently of it. In the field of geometry, on the other hand, there is a Latin translation from the 12th century for an Islamic work on spherical trigonometry, which contains in particular the sine theorem.

Research history

While the writings of Islamic mathematicians were highly regarded in the European High and Late Middle Ages, attitudes towards them changed in the course of the Renaissance. Mathematical research now concentrated primarily on the translation and commentary on the ancient Greek scripts, which were gradually becoming available again in Latin or their original language; the advances in Islamic mathematics, however, were neglected and partially forgotten. In the centuries that followed, this led to the majority of mathematicians and mathematicians adopting a Eurocentric view that constructed a direct line of development from Greek mathematics to modern Western mathematics.

The achievements of Islamic mathematicians were only rediscovered by Western mathematicians in the 19th century: In his comprehensive Histoire des mathématiques (1758) , Jean-Étienne Montucla wrote that Arabic-speaking mathematicians only dealt with second-degree equations, as Franz Wöpcke pointed out in 1851 in his dissertation on the algebra of Omar Chayyam that he had systematically dealt with third-degree equations. He published translations of previously unknown mathematical manuscripts, such as the algebra of al-Karaji. Together with Jean Jacques and Louis Pierre-Eugène Sédillot and Joseph Toussaint Reinaud , he is considered to be the founder of the history of science research on Islamic mathematics. In numerous works Eilhard Wiedemann dealt with the history of the Arabic sciences, in particular astronomy and the mathematics on which it is based. In his Introduction to the history of science (1927) , George Sarton finally overcame the Eurocentric view and shaped the modern understanding of an important role played by Arabic-language science for the preservation and independent further development of ancient knowledge as well as for the transfer of knowledge to Europe. Contemporary mathematicians such as Roshdi Rashed , John Lennart Berggren or Jan Hogendijk deal intensively with the mathematics of the Islamic heyday, so that today there is a clearer picture of the scientific progress of this epoch.

literature

• J. Lennart Berggren : Mathematics in Medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 .
• J. Lennart Berggren: Episodes in the Mathematics of Medieval Islam . 2nd Edition. Springer, New York 2016, ISBN 978-1-4939-3778-3 .
• Franka Miriam Brückler: History of Mathematics compact - The most important things from arithmetic, geometry, algebra, number theory and logic . Springer, 2017, ISBN 978-3-662-55351-0 .
• Helmuth Gericke : Mathematics in Antiquity and the Orient . Springer, Berlin / Heidelberg / New York / Tokyo 1984, ISBN 3-540-11647-8 , Section 3.3 Mathematics in the countries of Islam .
• Dietmar Herrmann: Mathematics in the Middle Ages - The history of mathematics in the West with its sources in China, India and Islam . Springer, Berlin / Heidelberg 2016, ISBN 978-3-662-50289-1 , chap. 4 Mathematics of Islam up to 1400 .
• Luke Hodgkin: A History of Mathematics - From Mesopotamia to Modernity . Oxford University Press, New York 2005, ISBN 0-19-852937-6 , 5. Islam, neglect and discovery.
• Victor J. Katz : A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , Chapter 9 The Mathematics of Islam .
• Fuat Sezgin : History of Arabic Literature, Volume V: Mathematics. Up to approximately 430 H . Brill, Leiden 1974, ISBN 90-04-04153-2 .
• Fuat Sezgin: Science and Technology in Islam I . Institute for the History of the Arab-Islamic Sciences, Frankfurt am Main 2003, ISBN 3-8298-0067-3 ( ibttm.org [PDF; accessed on May 27, 2018]).
• Hans Wußing : 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , chap. 5 Mathematics in the Lands of Islam .

Web links

• Index of Islamic mathematics. In: MacTutor History of Mathematics archive . University of St Andrews, February 2016, accessed March 28, 2018 . 
• Jan Hogendijk : Bibliography of Mathematics in Medieval Islamic Civilization. January 13, 1999, accessed May 6, 2018 . 

Individual evidence

1. ^ Hans Wußing: 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , p. 222 .
2. ↑ Dietmar Herrmann: Mathematics in the Middle Ages - The history of mathematics in the West with its sources in China, India and Islam . Springer, Berlin / Heidelberg 2016, ISBN 978-3-662-50289-1 , p. 139 .
3. ↑ ^{a b} Heinz-Wilhelm Alten et al .: 4000 years of algebra: history - cultures - people . 2nd Edition. Springer, Berlin / Heidelberg 2014, ISBN 978-3-642-38238-3 , pp. 156 .
4. ^ Hans Wußing: 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , p. 223 .
5. ↑ Heinz-Wilhelm Alten et al .: 4000 years of algebra: history - cultures - people . 2nd Edition. Springer, Berlin / Heidelberg 2014, ISBN 978-3-642-38238-3 , pp. 157 f .
6. ↑ ^{a b} Dietmar Herrmann: Mathematics in the Middle Ages - The history of mathematics in the West with its sources in China, India and Islam . Springer, Berlin / Heidelberg 2016, ISBN 978-3-662-50289-1 , p. 143 .
7. ↑ Heinz-Wilhelm Alten et al .: 4000 years of algebra: history - cultures - people . 2nd Edition. Springer, Berlin / Heidelberg 2014, ISBN 978-3-642-38238-3 , pp. 158 .
8. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 2 .
9. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 5 .
10. ↑ Dietmar Herrmann: The ancient mathematics - A history of Greek mathematics, its problems and solutions . Springer, Berlin / Heidelberg 2014, ISBN 978-3-642-37611-5 , pp. 406 f .
11. ↑ Fuat Sezgin: Science and Technology in Islam I . Institute for the History of Arabic-Islamic Sciences, Frankfurt am Main 2003, ISBN 3-8298-0067-3 , p. 9 .
12. ^ Hans Wußing: 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , p. 97-100 .
13. ↑ ^{a b} Franka Miriam Brückler: History of Mathematics compact - The most important things from arithmetic, geometry, algebra, number theory and logic . Springer, 2017, ISBN 978-3-540-76687-2 , pp. 16 .
14. ^ Hans Wußing: 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , p. 241 .
15. ↑ Fuat Sezgin: Science and Technology in Islam I . Institute for the History of Arabic-Islamic Sciences, Frankfurt am Main 2003, ISBN 3-8298-0067-3 , p. 13 .
16. ^ Hans Wußing: 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , p. 237 .
17. ↑ Menso Folkerts: The oldest Latin script on Indian arithmetic according to al-Ḫwārizmī . Bavarian Academy of Sciences, Munich 1997, ISBN 978-3-7696-0108-4 .
18. ^ Kurt Vogel : Mohammed ibn Musa Alchwarizmi's Algorismus; the earliest textbook on calculating with Indian numerals. After the only (Latin) manuscript (Cambridge Un. Lib. Ms. Ii. 6.5) in facsimile with transcription and commentary edited by Kurt Vogel . O. Zeller, Aalen 1968 ( hathitrust.org [accessed October 30, 2019]).
19. ^ John N. Crossley, Alan S. Henry: Thus Spake al-Khwārizmī: A Translation of the Text of Cambridge University Library Ms. Ii.vi.5 . In: Historia Mathematica . tape 17 , no. 2 , 1990, p. 103-131 , doi : 10.1016 / 0315-0860 (90) 90048-I .
20. ↑ Franka Miriam Brückler: History of Mathematics compact - The most important things from arithmetic, geometry, algebra, number theory and logic . Springer, 2017, ISBN 978-3-540-76687-2 , pp. 17 .
21. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 33 .
22. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 35 .
23. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 34 .
24. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 39 .
25. ↑ ^{a b} J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 42 .
26. ↑ ^{a b} J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 40 f .
27. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 270 .
28. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 270 .
29. ↑ Brückler, Franka Miriam: History of Mathematics compact: The most important things from analysis, probability theory, applied mathematics, topology and set theory. Springer-Verlag, 2017, ISBN 978-3-662-55573-6 , p. 94
30. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 112 f .
31. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 271 .
32. ↑ Helmuth Gericke : Mathematics in antiquity and the Orient . Springer, Berlin / Heidelberg / New York / Tokyo 1984, ISBN 3-540-11647-8 , pp. 214 .
33. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 111 f .
34. ↑ Fuat Sezgin: Science and Technology in Islam I . Institute for the History of Arabic-Islamic Sciences, Frankfurt am Main 2003, ISBN 3-8298-0067-3 , p. 13-14 .
35. ↑ Heinz-Wilhelm Alten et al .: 4000 years of algebra: history - cultures - people . 2nd Edition. Springer, Berlin / Heidelberg 2014, ISBN 978-3-642-38238-3 , pp. 175 .
36. ↑ Heinz-Wilhelm Alten et al .: 4000 years of algebra: history - cultures - people . 2nd Edition. Springer, Berlin / Heidelberg 2014, ISBN 978-3-642-38238-3 , pp. 150, 176 .
37. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 137 f .
38. ↑ Dietmar Herrmann: Mathematics in the Middle Ages - The history of mathematics in the West with its sources in China, India and Islam . Springer, Berlin / Heidelberg 2016, ISBN 978-3-662-50289-1 , p. 157-159 .
39. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 8 .
40. ↑ Louis Charles Kapinski: Robert of Chester's Latin translation of the Algebra of al-Khowarizmi . Macmillan, New York 1915, pp. 16 ( wilbourhall.org [PDF; accessed October 30, 2019]).
41. ^ Hans Wußing: 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , p. 239 .
42. ↑ Dietmar Herrmann: Mathematics in the Middle Ages - The history of mathematics in the West with its sources in China, India and Islam . Springer, Berlin / Heidelberg 2016, ISBN 978-3-662-50289-1 , p. 156-161 .
43. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 113 .
44. ↑ Heinz-Wilhelm Alten et al .: 4000 years of algebra: history - cultures - people . 2nd Edition. Springer, Berlin / Heidelberg 2014, ISBN 978-3-642-38238-3 , pp. 176 .
45. ↑ Franka Miriam Brückler: History of Mathematics compact - The most important things from arithmetic, geometry, algebra, number theory and logic . Springer, 2017, ISBN 978-3-540-76687-2 , pp. 105-107 .
46. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 115 .
47. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 273 .
48. ^ Hans Wußing: 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , p. 239 .
49. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 114 .
50. ↑ Heinz-Wilhelm Alten et al .: 4000 years of algebra: history - cultures - people . 2nd Edition. Springer, Berlin / Heidelberg 2014, ISBN 978-3-642-38238-3 , pp. 178 .
51. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 273 f .
52. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 115-119 .
53. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 119 .
54. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 120 f .
55. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 121-123 .
56. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 279 .
57. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 123-125 .
58. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 125-127 .
59. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 127-129 .
60. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 287 .
61. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 131-136 .
62. ^ Hans Wußing: 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , p. 248 .
63. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 136-137 .
64. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 306 .
65. ^ Hans Wußing: 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , p. 95 .
66. ^ Hans Wußing: 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , p. 95-96 .
67. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 149 .
68. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 146 .
69. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 307 .
70. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 147-149 .
71. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 149-153 .
72. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 315 .
73. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 153-156 .
74. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 175-177 .
75. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 177-179 .
76. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 184-190 .
77. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 311 .
78. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 195 .
79. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 195 f .
80. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 203-207 .
81. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 78 .
82. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 78 f .
83. ↑ Christoph J. Scriba , Peter Schneider : 5000 years of geometry - history, cultures, people . 3. Edition. Springer, Heidelberg a. a. 2010, ISBN 978-3-642-02361-3 , pp. 164 .
84. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 85 .
85. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 93-97 .
86. ^ J. Lennart Berggren: Mathematics in medieval Islam . Springer, Heidelberg a. a. 2011, ISBN 978-3-540-76687-2 , pp. 97-104 .
87. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 301 .
88. ↑ Christoph J. Scriba, Peter Schneider: 5000 years of geometry - history, cultures, people . 3. Edition. Springer, Heidelberg a. a. 2010, ISBN 978-3-642-02361-3 , pp. 173 f .
89. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 301-303 .
90. ↑ Franka Miriam Brückler: History of Mathematics compact - The most important things from arithmetic, geometry, algebra, number theory and logic . Springer, 2017, ISBN 978-3-540-76687-2 , pp. 92-97 .
91. ↑ Brückler, Franka Miriam: History of Mathematics compact: The most important things from analysis, probability theory, applied mathematics, topology and set theory. Springer-Verlag, 2017, ISBN 978-3-662-55573-6 , p. 68
92. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 282 f .
93. ↑ Heinz-Wilhelm Alten et al .: 4000 years of algebra: history - cultures - people . 2nd Edition. Springer, Berlin / Heidelberg 2014, ISBN 978-3-642-38238-3 , pp. 183 .
94. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 285-287 .
95. ^ JL Berggren: Episodes in the Mathematics of Medieval Islam . 2nd Edition. Springer, New York 2016, ISBN 978-1-4939-3778-3 , pp. 140-143 .
96. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 292-294 .
97. ^ JL Berggren: Episodes in the Mathematics of Medieval Islam . 2nd Edition. Springer, New York 2016, ISBN 978-1-4939-3778-3 , pp. 236-242 .
98. ^ JL Berggren: Episodes in the Mathematics of Medieval Islam . 2nd Edition. Springer, New York 2016, ISBN 978-1-4939-3778-3 , pp. 228-243 .
99. ^ JL Berggren: Episodes in the Mathematics of Medieval Islam . 2nd Edition. Springer, New York 2016, ISBN 978-1-4939-3778-3 , pp. 226-228 .
100. ↑ Franka Miriam Brückler: History of Mathematics compact - The most important things from arithmetic, geometry, algebra, number theory and logic . Springer, 2017, ISBN 978-3-540-76687-2 , pp. 144 .
101. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 295 .
102. ^ Muhammad Qasim Zaman: Transmitters of authority and ideas across cultural boundaries, eleventh to eighteenth century . In: Michael Cook (Ed.): The new Cambridge history of Islam . 3. Edition. Cambridge University Press, Cambridge, UK 2010, ISBN 978-0-521-51536-8 , pp. 600-603 .
103. ^ Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 325 .
104. ^ ^{A b} Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 267 .
105. ^ ^{A b} Albert Hourani : The history of the Arab peoples. Told on until the Arab Spring by Malise Ruthven . S. Fischer, Frankfurt 2014, ISBN 978-3-10-403359-4 , pp. 121 : "Philosophy remained alive, but it became a private matter - often by medical professionals - which was followed with caution and which often aroused suspicion."
106. ^ Hunt Janin: The pursuit of learning in the Islamic world, 610-2003 . McFarland, Jefferson, NC [et. a.] 2007, ISBN 978-0-7864-2904-2 , pp. 83 ( limited preview in Google Book search).
107. ^ W. Montgomery Watt: The Faith and Practice of Al-Ghazali . George Allen and Unwin Ltd, London 1953 ( ghazali.org [accessed on May 21, 2018]): “He was the leader in Islam's supreme encounter with Greek philosophy - that encounter from which Islamic theology emerged victorious and enriched, and in which Arabic Neoplatonism received a blow from which it did not recover. "
108. ↑ ʻAbd-Elṣamad ʻAbd-Elḥamīd: Introduction . In: Abū-Ḥamid Muḥammad al-Ghazālī Elschazlī: The criterion of action. From the Arab. transl., with an introduction, with annotation and indices ed. from ' Abd-Elṣamad ' Abd-Elḥamīd . Scientific Book Society, Darmstadt 2006, ISBN 3-534-19039-4 , pp. 59 : “[Al-Ghazālī] therefore wants to show how unacceptable and groundless is the attempt to combine Islamic ethics with Greek, for an important characteristic of Islamic ethics, in contrast to Greek, is belief in God and in that Beyond with all the obligations that come with it. Neither Plato and Aristotle speak of such a relationship, nor do the Islamic philosophers. "
109. ↑ Wolfgang Hein: Mathematics in the Middle Ages - From Abacus to Numbers Game . WBG, Darmstadt 2010, ISBN 978-3-534-23121-8 , p. 136 f .
110. ^ ^{A b c} Victor J. Katz: A History of Mathematics - An Introduction . 3. Edition. Addison-Wesley / Pearson, Boston a. a. 2009, ISBN 978-0-321-38700-4 , pp. 317 .
111. ↑ Wolfgang Hein: Mathematics in the Middle Ages - From Abacus to Numbers Game . WBG, Darmstadt 2010, ISBN 978-3-534-23121-8 , p. 137 .
112. ^ Hans Wußing: 6000 years of mathematics - a cultural-historical journey through time . 1. From the beginning to Leibniz and Newton . Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77189-0 , p. 277 .
113. ↑ Wolfgang Hein: Mathematics in the Middle Ages - From Abacus to Numbers Game . WBG, Darmstadt 2010, ISBN 978-3-534-23121-8 , p. 143 .
114. ^ ^{A b} Luke Hodgkin: A History of Mathematics - From Mesopotamia to Modernity . Oxford University Press, New York 2005, ISBN 978-0-19-852937-8 , pp. 102 .
115. ^ Jean-Étienne Montucla: Histoire des mathématiques . tape 1 . Paris 1758, p. 359 f . ( bnf.fr [accessed May 27, 2018]).
116. ↑ Fuat Sezgin: Science and Technology in Islam I . Institute for the History of Arabic-Islamic Sciences, Frankfurt am Main 2003, ISBN 3-8298-0067-3 , p. 2 .

This article was added to the list of excellent articles in this version on May 25, 2018 .