Rod (unit)

Half a Prussian rod at the historic town hall in Münster
(since the Prussian rod was twelve feet, half the rod was actually a fathom )

The rod is both an ancient unit of length and a traditional measuring device for measuring length . In German-speaking countries, the rod was usually abbreviated with the symbol °.

Different countries and professions used almost 20 different lengths of rod between 3 and 9 meters, but mostly from 3.6 to 5 meters or 1½ to 3  fathoms . They were (with two exceptions) integral multiples of the commonly used unit foot (approx. 30 cm).

overview

In a clear context, the term rod was often used synonymously with the square rod or quarter rod, i.e. the corresponding area measure . In connection with the hoof there was also a so-called flat rod . It corresponded to the area of ​​a tail width of the hooves. For the hooves measured with the Saxon king's rod , this was 1 rod × 270 rods, i.e. 270 Saxon king square rods or one twelfth of the total land hooves, i.e. almost two hectares.

The rod length measure has been used with different definitions around the world. Their length always exceeded one and a half fathoms on the one hand and on the other hand they never measured more than five fathoms. In practice, however, custom-made rods between about three and five meters have been used almost everywhere. A distinction can be made between ordinary and special field knife rods . The special ones were preferred by the old surveyors , as only they allowed the length of the diagonal of a square to be measured to be expressed with great precision in a rational and integer value, thus avoiding the calculation with the unwieldy, irrational square root of two . The Rutenmaß came mainly in land surveying and in building construction and civil engineering are used. The rod was used even longer as a rod in the Anglo-American countries, where it is also called pole or perch .

Anglo-American system of measurement

Physical unit
Unit name	rod
Unit symbol	${\displaystyle \mathrm {rd} }$
Physical quantity (s)	length
Formula symbol	${\displaystyle l}$
dimension	${\displaystyle {\mathsf {L}}}$
system	Anglo-American system of measurement
In SI units	${\displaystyle \mathrm {1\,rd=5{,}029\,2\;m} }$
Named after	english rod "rod"
Derived from	Chain

• The English rod (rod) measures 5½  yards , equal to 16½  feet or 198  inches . Thus the length of the English rod is exactly (16½ × 0.3048 =) 5.0292 meters .
• The width of the metrological reference field Oxgang was defined as 40 rods. This width, furlong , also known as the plow furrow length, is divided into ten measurement chains. Each chain, English chain containing four rods, so 66 feet. The total field width is therefore 660 English feet. The English mile contains exactly eight fields and therefore exactly 320 English rods.

The rod is hardly used today; the foot has taken its place .

Typical rods

Depending on their respective relationship to the size of the foot, a distinction can be made between around one and a half dozen different types of rods. Whereby the surveyors used rods over three or four fathoms - such as the 30 foot long king rods  - due to their unwieldy length in practice almost always only as half rods. It was also quite common for two or three different types of rods to be used in parallel in one and the same system of measurements. For example, it could be that the larger distances, for example the mile , were a multiple of the two smooth 16-foot rods, whereas the surveyors used a seven- smooth 14-foot rod and the builders eventually used their three-smooth twelve-foot rod grabbed.

Name  (of the rod type)	foot	smoothness	0.3 m long	Remarks
5 fathoms = king's rod	30th	5	9.00 m	The king's hooves were theoretically measured at thirty feet in king's rods.
Double field tail	28	7th	8.40 m	Rods of four fathoms or more, even if they occasionally appeared as theoretical definitions , turned out to be too long in practice to be able to function as a specific measuring device . In such cases, the surveyors almost invariably used the corresponding half-rod.
Four and a half fathom rod	27	3	8.10 m
Five double step rod	25th	5	7.50 m
Four fathom rod	24	3	7.20 m
Arpenteur rod	22nd	11	6.60 m	The eleven-smooth Arpenteur rod was the surveyor's rod in France.
Three and a half fathom rod	21st	7th	6.30 m	These one and a half field rods were only found very rarely.
Gromatici double rod	20th	5	6.00 m	Sometimes the rod was also defined as a 20-foot measure. See: Oldenburg, old.
Three fathom rod	18th	3	5.40 m	In France it was also known as the “king's rod”. They existed elsewhere too.
Surveyor rod	16½	11	4.95 m	The practical 16½-foot rod is the most commonly used eleven-smooth survey rod.
Woodrod	16	2	4.80 m	Fourfold doubling of the feet resulted in a popular measure of length: the forest rod.
"Meadow rod"	15th	5	4.50 m	This 1½ gromanici rod is half of the 30 foot king rod from the Königshufe.
Field rod	14th	7th	4.20 m	The seven-smooth 14 foot tail was generally preferred by surveyors.
Five-step tail	12½	5	3.75 m	The five-smooth 2½ double-step rod was also used in Frankfurt am Main, for example.
Construction or work rod	12	3	3.60 m	The threefold twelve-foot construction or work rod is also known as the "small rod".
Arpenteur half-rod	11	11	3.30 m	Since the Arpenteur rod was very long, the measuring instrument was often half of it.
Gromatici rod	10	5	3.00 m	The Roman two-double-step rod was used elsewhere as well.

The most common types of rods were medium-sized, between fourteen and sixteen and a half feet. The builders, for their part, mostly preferred the somewhat shorter twelve-foot rod.

Ordinary rods

Ordinary rods are those rods whose ratio to the foot size does not exceed the arithmetic smoothness of five, i.e. two, three or at most five smooth. These ordinary rods were ideally suited for pure length measurement. The old Roman rod (pertica) measured two double steps, equal to ten Roman feet, and was therefore five smooth. The threefold twelve-foot rod, on the other hand, measures two fathoms and was mostly called construction or work rod . The two-smooth 16-foot rod was generally referred to as the forest rod in the German-speaking area . It later became the legal standard rod within the Holy Roman Empire , whereas previously this was mostly the two and a half fathoms long 15-foot rod. Occasionally there were also 18-foot rods of three fathoms, less often 20 or 21-foot rods or even longer rods.

• The Roman pertica was the ten-foot rod of the Gromatici . It was the equivalent of two Roman double steps, a little more than 2.96 meters.
• The Prussian rod was a twelve-foot rod. According to the official conversion, it corresponded to exactly 1,669.56 Parisian lines , i.e. about 3.77 m.
• The kulmish rod was the measure in East Prussia until 1816. 1 kulmic rod was 4.3892 m, 1 kulmic foot was 26.261 cm and one mile was 7,900,500 m.
• The Polish rod was a 15-foot rod. The underlying dimension is the old Kulmer foot, which is around 127.7 Parisian lines, approx. 288.1 mm. The Polish rod therefore measures around 4.32 m.
• The Frankish rod was a 16-foot rod, with the Nuremberg foot being twenty-five twenty-fourth of a Bavarian foot . Empirically, the value of the large Franconian rod was a good 4.86 m.

All of these common rods were shunned by the ancient surveyors because they did not allow the extremely practical rational triangulation of the square to be accomplished. To make this possible, they used their own seven- or eleven-smooth rods.

The officials entrusted with the taxation of landed property did not always understand why the surveyors wanted to measure with their special rods. Although very many cases are known in which the official taxation area measurements were identical to the special rod measurements of the surveyors, in other cases there was also a double standard of ordinary and special rod measurements. The surveyors used their special, seven- or eleven-smooth surveying rods for their actual work in the field. If necessary, however, at the very end of their survey work, they converted the final results into area values ​​for ordinary square rods. Or, to save yourself this conversion, they simply divided the 15- or 16-foot rods by fourteen. This gave them an initially unofficial working foot that was one or two-fourteenths longer. Not infrequently, this new measuring foot later became the official one and / or was adopted by neighboring countries. This explains the omnipresent presence of the ratio 15:14 or 16:14 between different feet.

Special surveyors rods

Special field rods are those rods whose ratio to the foot is seven or eleven smooth. Since early antiquity, they have been the preferred choice for field surveying. Until well into modern times, traditional land surveying without it was not possible in practice, or at least made considerably more difficult. Only after the general distribution of slide rules at the end of the 18th century were the special field rods no longer indispensable.

The smooth field rod

The 14-foot rod is the field rod par excellence. It enjoyed widespread use and great popularity. For the above-mentioned Franconian forest rod at 16 feet there was also a Franconian field rod at 14 feet. This was also used in Meiningen , for example, with the empirical value of 4255.622 mm.

The eleven smooth Arpenteur or Surveyor rods

Three field rods (as well as, for example, the Spanish surveyor rope) are eleven smooth:

• The simple eleven-foot rod was mainly practiced as the half rod of the French arpenteur rod. This type of rod was sometimes found elsewhere.
• The important 16½-foot rod, being one and a half times that of the half Arpenteur rod just mentioned, was certainly the best eleven-smooth rod in practice. It is without a doubt eleven smooth, since negative whole-number powers can also be allowed in the definition of the smoothness: 2 ⁻¹  × 3 ¹  × 5 ⁰  × 7 ⁰  × 11 ¹  = 16½. This measuring stick of medium length is very easy to handle. It's neither too short nor too long. The Surveyor rod is thus superior to the French 22-foot definition. Surveyor rods of the English surveyor rod type are also occasionally found in the Holy Roman Empire. Mostly the seven smooth 14-foot rods were preferred here. The result is the same, since the rational triangulation of the square is possible with both seven-smooth as well as eleven-smooth measuring rods.
• The whole 22-foot rod was the official surveyor rod of the French arpenteurs. The French surveyors did their calculations in the official unit, but in practice they often only worked with half the measuring stick, since the whole thing, over seven meters long, was rather unwieldy.

The Spanish 24 ¾ foot rope was another eleven smooth gauge. This official Spanish measure, called Cuerda , was defined as ninety-nine quarters of the Spanish foot. In some regional systems of measurement, there were also occasional measures other than the rod, for example the measuring chain, seven or eleven smooth.

Surveying rods smoother than eleven

Thirteen, seventeen, or nineteen smooth rods were not used by the surveyors. This is explained by the fact that it simply makes no sense to artificially and at the same time uselessly complicate the calculations by introducing a new, high prime factor arbitrarily. In rare cases, one can encounter ratios worse than eleven. However, these almost always turn out to be artificially adapted. The Saxon field knife rod was recently defined as exactly 182 (new) Saxon customs. 182 (2 × 7 × 13) is an even number 13. A factor that has absolutely never been used in traditional metrology. In reality it was a 15-foot rod with the same foot size as that of the Hamburg Geestrute or the Stuttgart foot size. In all three cases it is the measure of the old Liudolfingian king's foot. ( King's Rods of the Franconian Hufen ).

A big exception is the Dutch rod, which actually measures thirteen Dutch feet. Remarkably, the Dutch foot is divided into only eleven inches. Twelve Dutch inches is the length of the Cyrenean foot , which in turn is 25:24 of the Roman foot. The Dutch foot is the so-called Cyrenean trading foot. The Dutch metrologists now considered it opportune to choose a rod of thirteen of these feet, as they had recognized that ten such rods contain approximately exactly 132 Spanish feet on the one hand and 128 Cologne feet on the other. The theoretical error that occurs in this equation is only (2 ¹³ × 3 ⁵  ÷ 5 ⁵ × 7 ² × 13 =) 0.0016 percent. It goes without saying that the Spanish foot was an important reference measure in the Spanish Netherlands. Of course, in Holland, the Cologne foot was also very important, since this is the Rhenish trading foot, so it is in the ratio 11:12 to the actual Rhenish foot. For these reasons, the Dutch metrologists found it acceptable to include the prime number 13 in their system of measurements. The prime factors seven and eleven, on the other hand, made the calculations of the traditional field survey much easier. Hence the spread of these special field rods.

The rational triangulation of the square

Rational triangulation of the square by approximating the root 2 equal to 99 ÷ 70, with an accepted error of 0.0051%.

The numerical value of the square root two is irrational , for a triangulation you need a suitable approximate value as a rational numerical value . Since ancient times mathematicians and surveyors tried to express the length value of the diagonal of a square in this way. They approached the irrational numerical value of the root two in a completely comparable way, just as we still do today when we specify the root two as a rounded value in a decimal fraction : 1 + (4142 / 10,000) or 1 + (414 213 562/1000000000).

Already in the first third of the second millennium (−1700 ± 100) BC. The Babylonians knew the good approximate sexagesimal value 1 + 24 × 60 ⁻¹ + 51 × 60 ⁻² + 10 × 60 ⁻³   = 30547 ÷ 21600 = 1.41421 296 . (Cf. the clay tablet YBC 7289 ) Since √2 - (30547 ÷ 21600) ≈ 1.41421356 - 1.41421296 = 0.000000599, the ancient Babylonians knew the value of the root two to five full, correct decimal places exactly with an error of around half a decimal point Millionth.

The Babylonians therefore measured the diagonal of their nippur cubit to be exactly 42.4263 8 finger widths , as indicated by another sexagesimal number noted on this clay tablet (vs. real approximately 42.426407 finger widths). In millimeters and based on the seven smooth value, this diagonal measures exactly (518.616 × (30547 ÷ 21600) =) 733.43347 mm according to the Babylonian approximation, compared to about 733.4337808637 mm in reality. In other words,  nearly four thousand years ago, the ancient Babylonians underestimated the diagonal of their square by less than 310.864 nanometers .

The surveyors' demand for precision results from their practice. The good smoothness was always more important for the convenience of the calculations than the need for too great, absolute accuracy. The above number 30547, factor of the excellent Babylonian approximation value, is eleven times the prime number 2777. The approximation is 2777-smooth, which is unfortunately a very bad smoothness , even worse, one that can only be called hideous . For this reason, various root-two approximation values ​​were examined very early on by the geometers, whereby the best possible smoothness was in the foreground. (Cf. French Méthodes d'approximation de racine carrée de deux.)

Theon

fraction	factorial smoothness	relative deviation	Actual use of the approximate value in question	rounded ratio ( precision )
3 ÷ 2	threefold	+ 6.0660%	Never used as it is far too imprecise in an indisputable way. Not practical.	3600
7 ÷ 5	seven smooth	- 1.0051%	In ancient Egypt at the beginning of the 3rd millennium BC Chr., Cf. the so-called construction remen.	600
17 ÷ 12	seventeen smooth	- 0.1735%	Not used. Relatively high prime factor and at the same time far less precise than 99:70.	100
99 ÷ 70	eleven smooth	+ 0.0051%	Very good approximation; omnipresent in surveying since ancient times.	3

Other, even more precise approximations were known, as the theon sequence of the table on the right shows: for example the value 239 ÷ 169 or 577 ÷ 408. However, these contain high prime factors. The fairly precise approximation 99 ÷ 70 is very suitable for land surveying. Example:  Assuming the legs of a right-angled isosceles triangle each measure exactly 99 centimeters, the hypotenuse value exceeds the length of 140 cm by only about 71.437 µm, i.e. about a fourteenth of a millimeter.

When the Greek mathematician Theon von Smyrna systematically examined the various root-two approximations and wrote a theoretical treatise on them, the more than satisfactory eleven-smooth approximation 99 ÷ 70 was certainly used by surveyors in practice for centuries, perhaps millennia . The 14-foot field rod, which, for example, the German geodesists  primarily used -  not only in the Middle Ages, but well into our modern times - were created for precisely this purpose. The same is true of the English 16 ½ foot survey rod and the French 22 foot one. Seven smooth rods (here another example of a 14-foot rod) and the eleven smooth surveyor rods (here the two best known) always contain the internal factor seven and eleven:

• The Kassel cadastral rod , a 14-foot field rod of fourteen Cologne feet, empirically 3,988760 meters.
• The English Surveyor's Rod, at (2 × 99 =) 198 inches, so 5½ yards equals 16½ feet or 5.0292 meters.
• The French arpenteur rod, at 22 king feet, so (22 × 9000 ÷ 27.706 mm) about 7.1465 meters.

The respective factors seven and eleven, which are included in the definition of these field rods, were decisive for the rational triangulation of the square with its approximation √2 ≈ 99 ÷ 70 being possible. Note that even the approximately 5000 year old Egyptian royal cell, which in turn goes back directly to the Nippurelle -  this time in its digitus definition  - contains a factor of seven (1 cubit = 28 digiti), which in this regard for the ancient Egyptian geometers in their annual new ones Land surveying after the Nile flood was of course extremely practical.

The application of the rational approximation was as follows:

For example, the surveyors determined a square field 140 feet on a side. After that, they knew immediately and without further calculation that its diagonal was 2 × 99 = 198 feet. In the case of the eleven-smooth rod, it was exactly the opposite. A square field of 12 × 16½ = 198 feet on a side has a diagonal length of 280 feet. This approximate value was not used solely to determine the length of the diagonal. All the root-two factors occurring in the calculations could be replaced by 99:70. For example, the Saxon royal rod was created from the Franconian royal hoof (or the Franconian royal rod). In order to maintain the same areal measure with a different hoof cut, the Saxon royal rod had to be exactly the square root of 8 ÷ 9 multiplied by the value of the Franconian royal rod. This can be resolved in (2√2): 3. If you replace √2 with 99 ÷ 70, you get the simple ratio of 33:35. This relationship therefore exists between the old Saxon royal foot, which was preserved in the Saxon surveyor's rod, and the Franconian foot, which was preserved in the city of Nuremberg.

Example of a diagonally derived system of measurements:

The rational triangulation of the square was the inspiration for many systems of measurement. The English length and area measurements are a direct, diagonal derivation of the Roman measurements. The English metrological reference field was the so-called Oxgang , which measures 40 × 60 English surveyor rods. Whereby 40 rods equals a furlong , i.e. a plow furrow length. The area of ​​the Oxgang, the English small hooves, is fifteen English fields (acres) , but at the same time also twelve Roman portions of inheritance (heredia) . The two feet measure in a ratio of 36:35.

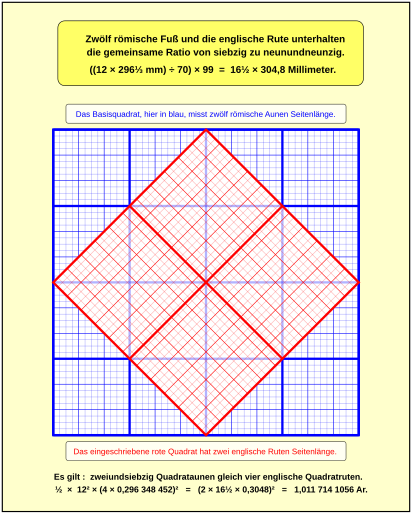
In a simplified form, the illustration shows the relationship between the English surveyor's rod and the late Roman 4-foot aune. The English system of measurement is derived directly from the Roman system of measurement through the rational triangulation of the square. The English field rod therefore measures: ((12 × 296⅓ mm) ÷ 70) × 99 = 16½ × 304.8 millimeters = 5.0292 meters. Quite a few similar relationships are known, also between the English and the old Rhenish foot.

Regional or national rod dimensions and their respective values

The following list is largely exhaustive , at least with regard to the rod dimensions of the Holy Roman Empire , which were maintained up to the 19th century . It also contains some important rod dimensions from neighboring countries such as France, Poland, Switzerland, Holland or Belgium, as well as England. The Italian rod dimensions are still missing from this list, as are those of the Baltic States and other Eastern and Southeastern European countries. Since most rod dimensions have existed as 12, 14, 15 and 16 foot rods in the course of history and depending on the region, before they were later normalized as legal 16 foot rods within the Holy Roman Empire, this list adds if not already available, include the rod type in the name of the rod. However, existing, old names such as Geest, March or Cadastre were retained.

0 Residential city	0Country or Region Note	0Name of the rod size	Foot ratio	Foot in mm	Rod in mm	Rod 2 in m²	Ref.	smoothness
0 Paris	0 Kingdom of France	0 French Arpenteur rod	22nd	324,839	7146,467	51.0720	(1)	11
0 Oldenburg	0 County of Oldenburg	0 Old Oldenburg rod	20th	295.879	5917,580	35.0178	(2)	5
0 Paris	0 Kingdom of France	0 French royal rod	18th	324,839	5847.110	34.1887	(3)	3
0 Bremen	0 Free Hanseatic City	0 Large Bremen rod	20th	289,350	5787,000	33.4894	(4)	5
0 Antwerp	0 Duchy of Brabant	0 Large Antwerp rod	20th	286,800	5736,000	32.9017	(5)	5
0 Altenburg	0 Saxe-Gotha-Altenburg	0 Large Altenburg rod	20th	283.794	5675,880	32.2156	(6)	5
0 Brussels	0 Kingdom of Belgium	0 Large Belgian rod	20th	275.750	5515,000	30.4152	(7)	5
0 Oldenburg	0 Duchy of Oldenburg	0 New Oldenburg rod	18th	295.879	5325.822	28.3644	(8th)	3
0 London	0 United Kingdom	0 English surveyor rod	16½	304.797	5029.155	25.2924	(9)	11
0 Neustrelitz	0 Mecklenburg-Strelitz	0 Prussian forest rod	16	313.854	5021.656	25.2170	(10)	2
0 Wiesbaden	0 Duchy of Nassau	0 Metric "field rod" (1853)	10	500,000	5000,000	25.0000	(11)	5
0 Nuremberg	0 Free imperial city	0 Franconian woodrod	16	303.973	4863,568	23.6543	(12)	2
0 Prague	0 Kingdom of Bohemia	0 Bohemian woodrod	16	297.560	4760,960	22.6667	(13)	2
0 Stockholm	0 Kingdom of Sweden	0 Swedish forest rod	16	296.906	4750.496	22.5672	(14)	2
0 Neuchâtel	0 Principality of Neuchâtel	0 Neuchâtel vineyard route	16	293.258	4692.128	22.0161	(15)	2
0 Hanover	0 Electorate of Hanover	0 Calenberg woodrod	16	292.095	4673.515	21.8417	(16)	2
0 Arolsen	0 Waldeck- Pyrmont	0 Arolsener woodrod	16	291,365	4661,840	21.7328	(17)	2
0 Schwerin	0 Mecklenburg	0 Mecklenburg forest rod	16	291,000	4656,000	21.6783	(18)	2
0 Karlsruhe	0 Baden-Durlach	0 Old Karlsruhe forest rod	16	291,000	4656,000	21.6783	(19)	2
0 Buckeburg	0 Schaumburg-Lippe	0 Buckeburg woodrod	16	290.100	4641,600	21.5445	(20)	2
0 Detmold	0 Lippe-Detmold	0 Detmold woodrod	16	289,513	4632.208	21.4574	(21)	2
0 Bremen	0 Free Hanseatic City	0 Bremen woodrod	16	289,350	4629,600	21.4332	(22)	2
0 Schwerin	0 Mecklenburg-Schwerin	0 Rostock woodrod	16	287.699	4603.191	21.1894	(23)	2
0 Gotha	0 Saxe-Gotha	0 Gotha woodrod	16	287.618	4601.888	21.1774	(24)	2
0 Cologne	0 Historic Rhineland	0 Cologne forest rod	16	287,393	4598.280	21.1442	(25)	2
0 Neuchâtel	0 Principality of Neuchâtel	0 Neuchâtel forest rod	16	287,150	4594,400	21.1085	(26)	2
0 Hamburg	0 Free Hanseatic City	0 Hamburg geestrute	16	286,572	4585.144	21.0235	(27)	2
0 Gera	0 Reuss younger line	0 Geraer Waldrute	16	286.197	4579,152	20.9686	(28)	2
0 Braunschweig	0 Braunschweig-Wolfenbüttel	0 Brunswick woodrod	16	285,362	4565.798	20.8465	(29)	2
0 Dresden	0 Electorate of Saxony	0 Dresden street route	16	283.190	4531,042	20.5303	(30)	2
0 Greiz	0 Reuss older line	0 Saxon forest rod	16	283.190	4531.040	20.5303	(31)	2
0 Rudolstadt	0 Schwarzburg-Rudolstadt	0 Rudolstädter Waldrute	16	282,200	4515,200	20.3870	(32)	2
0 Weimar	0 Saxe-Weimar-Eisenach	0 Weimar woodrod	16	281,980	4511,680	20.3553	(33)	2
0 Frankfurt am Main	0 Free imperial city	0 Frankfurter Waldrute	16	281,923	4510.760	20.3470	(34)	2
0 Hildesheim	0 Principality of Hildesheim	0 Hildesheim forest rod	16	280.175	4482,800	20.0955	(35)	2
0 Warsaw	0 Kingdom of Poland	0 Polish meadow rod	15th	288,000	4320,000	18.6624	(36)	2
0 Danzig	0 Free Hanseatic City	0 Danzig meadow rod	15th	286.885	4303.278	18.5182	(37)	3
0 Dresden	0 Electorate of Saxony	0 Saxon field knife rod	15th	286,337	4295.050	18.4475	(38)	5
0 Leipzig	0 Margraviate of Meissen	0 Leipzig meadow rod	15th	285.639	4284,583	18.3577	(39)	3
0 Meiningen	0 Saxony-Meiningen	0 Franconian field rod	14th	303.973	4255.622	18.1103	(40)	7th
0 Gotha	0 Saxe-Gotha	0 Gotha field rod	14th	287.618	4026,652	16.2139	(41)	7th
0 Hamburg	0 Free Hanseatic City	0 Hamburg marching rod	14th	286,572	4012.001	16.0962	(42)	7th
0 kassel	0 Hessen-Kassel	0 Kassel cadastral rod	14th	284,911	3988.760	15.9102	(43)	7th
0 Erfurt	0 Principality of Erfurt	0 Erfurt field rod	14th	283,260	3965,640	15.7263	(44)	7th
0 Sondershausen	0 Schwarzburg-Sondershausen	0 Sondershausen field rod	14th	282,500	3955,000	15.6420	(45)	7th
0 Vienna	0 Archduchy of Austria	0 Austrian work rod	12	316,081	3792,968	14.3866	(46)	3
0 Berlin	0 Kingdom of Prussia	0 Prussian work rod	12	313.854	3766.242	14.1846	(47)	3
0 Amsterdam	0 Spanish Netherlands	0 Dutch rod	13	283.133	3680,734	13.5478	(48)	13
0 Nuremberg	0 Free imperial city	0 Franconian work rod	12	303.973	3647.676	13.3055	(49)	3
0 Hanau	0 Electorate of Hesse	0 Hanauer Werkrute	12	297.458	3569,500	12.7413	(50)	3
0 Frankfurt am Main	0 Free imperial city	0 Roman work rod	12½	284.610	3557.630	12.6567	(51)	5
0 Emden	0 Electorate of Hanover	0 Calenberger work rod	12	292.095	3505.136	12.2860	(52)	3
0 Fulda	0 Principality of Fulda	0 Fulda work rod	12	282.880	3394,560	11.5230	(53)	3
0 Madrid	0 Kingdom of Spain	0 Spanish work rod	12	278.635	3343,620	11.1798	(54)	3
0 Christiania	0 Denmark-Norway	0 Danish-Norwegian Rode	10	313.763	3137,632	09.8447	(55)	5
0 Karlsruhe	0 Grand Duchy of Baden	0 New Baden Rod (1810)	10	300,000	3000,000	09.0000	(56)	5
0 Oldenburg	0 Duchy of Oldenburg	0 Oldenburg cadastral rod	10	295.879	2958.790	08.7544	(57)	5
0 Bern	0 Canton Bern	0 Old, small Bernese rod	10	293.258	2932,580	08.6000	(58)	5
0 Munich	0 Electorate of Bavaria	0 Small Bavarian rod	10	291.722	2917.215	08.5101	(59)	5
0 Munich	0 Kingdom of Bavaria	0 Small Bavarian rod	10	291.859	2918,592	08.5182		5
0 Stuttgart	0 Württemberg , Hohenzollern	0 Small Swabian rod	10	286,490	2864.903	08.2077	(60)	5
0 Wiesbaden	0 Duchy of Nassau	0 Metric "work rod" (1853)	10	250,000	2500,000	06.2500	(61)	5

Note: With one exception, this table does not contain any rods with exactly the same values, as in such cases it is only a matter of adopting an existing dimension. Example: In the Duchy of Schleswig a 16-foot rod was used that was identical to the Hamburg geestrange. Conversely, this list contains - very well - many cases in which it is actually about the same measure, but which was stored locally with only slightly different values. Deviations of less than ± 0.05% are still considered flawless in the old metrology, between ± 0.05% and ± 0.10% only as average and up to ± 0.15%, at best as very bad.

• The Old Testament also speaks of rods. One rod was equal to six large cubits , but historically, at different times, different cubits were used.

See also

• Dike digger rod
• Earth rod
• Hoof tail
• Hundreds of a rod
• Cubic field rod
• Cubic Engineer Rod
• Matrikularrute
• Manhole
• Street rod
• Toftrute

literature

• Otto Brandt: Documentary on measure and weight in Saxony . Saxon Ministry of the Interior, Dresden 1933.
• Fritz Verdenhalven : Old measurement and currency systems from the German-speaking area. What family and local history researchers are looking for. 2nd significantly increased and completely revised edition. Degener, Neustadt an der Aisch 1993, ISBN 3-7686-1036-5 .
• Johannes Langer: Local history forays through fields and places of the Ore Mountains and its foreland. Schwarzenberg / Saxony 1931

Individual evidence

1. ↑ WEA v. Schlieben, JV Monday: Complete handbook and textbook for all of the lower measurement skills . 3. Edition. Verlag der Ernst'schen Buchlassung, Quedlinburg and Leipzig 1845, p. 9 .
2. ^ Heinrich Walter: Königshufen, Waldhufen and Sächsische Acker . ( Memento of the original from March 16, 2012 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (PDF; 444 kB) In: New Archive for Saxon History, N ° 51, 1930, p. 4, center. 
3. ^ Angelo Martini: Manuals di metrologia . Edition Loescher, Turin 1883, p. 74.
4. ^ Angelo Martini: Manuals di metrologia . Edition Loescher, Turin 1883, p. 180.
5. ^ Angelo Martini: Manuals di metrologia . Edition Loescher, Turin 1883, p. 414.
6. ^ Angelo Martini: Manuals di metrologia . Edition Loescher, Turin 1883, p. 342.
7. ^ Angelo Martini: Manuals di metrologia . Edition Loescher, Turin 1883, p. 321.
8. ^ Angelo Martini: Manuals di metrologia . Edition Loescher, Turin 1883, p. 148.
9. ↑ Journal of the Royal Bavarian Statistical Bureau, first year 1869, p. 140: "Official compilation of the ratios for the conversion of the measurements and weights that have been valid in Bavaria in this part of the Rhine into those stipulated by the law of April 29, 1869, concerning the Maas and weight system , determined new measurements and weights.
10. ^ Angelo Martini: Manuals di metrologia . Edition Loescher, Turin 1883, p. 41.