Actinoids
|
Position in the periodic table
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Actinoids [ -noˈiːdə ] ("actinium-like"; Greek : ending -οειδής (-oeides) "similar") is a group name for certain similar elements . Attributed to it are the actinium and 14 in the periodic table following elements: thorium , protactinium , uranium and transuranic elements neptunium , plutonium , americium , curium , berkelium , californium , einsteinium , fermium , mendelevium , Nobelium and lawrencium . In the sense of the term, Actinium does not belong to the group similar to actinium, but the IUPAC nomenclature here follows practical usage. The former name Actinide does not correspond to the proposal of the Nomenclature Commission, since after this the ending "-id" for binary compounds such as z. B. Chloride is reserved; however, the designation is still allowed. All actinides are metals and are also known as elements of the actinium series.
|
89 Ac |
90 th |
91 Pa |
92 U |
93 Np |
94 Pu |
95 am |
96 cm |
97 Bk |
98 Cf |
99 it |
100 m |
101 Md |
102 No. |
103 Lr |
Definition of terms
- The transuranic elements are the elements with a higher atomic number than uranium , i.e. H. the actinides beginning with neptunium (93) are also transuranic elements.
- As transactinide are the elements with atomic numbers from 104 ( rutherfordium ). They follow the actinides in the periodic table . All transactinoids are also transuranic at the same time, since they have atomic numbers greater than those of uranium.
- In the context of nuclear fuel and radioactive waste, neptunium , americium , curium , berkelium and californium are also referred to as minor actinides .
- The actinide nuclides are heavy metals . In reactor physics , the concept of heavy metals is somewhat restricted in combustion calculations . In this context, only heavy metal nuclides that can be split by neutrons are referred to as heavy metals . All heavy metal nuclides from actinium 225 can be split, including all actinide nuclides. The masses of fission products and the masses of the heavy nuclides mainly formed by neutron capture in a nuclear reactor are usually given relative to the mass of the initially defined heavy metals .
Discovery and extraction
| element | year | method |
|---|---|---|
| neptunium | 1940 | Bombardment of 238 U with neutrons |
| plutonium | 1941 | Bombardment of 238 U with deuterons |
| Americium | 1944 | Bombardment of 239 Pu with neutrons |
| Curium | 1944 | Bombardment of 239 Pu with α-particles |
| Berkelium | 1949 | Bombardment of 241 Am with α-particles |
| Californium | 1950 | Bombardment of 242 cm with α-particles |
| Einsteinium | 1952 | As a product of nuclear weapon explosions |
| Fermium | 1952 | As a product of nuclear weapon explosions |
| Mendelevium | 1955 | Bombardment of 253 Es with α-particles |
| Nobelium | 1964-1968 | Shelling of 243 Am with 15 N or 238 U with 22 Ne or 249 Cf with 12 C. |
| lawrencium | 1961-1971 | Bombardment of 252 Cf with 10 B or 252 Cf with 11 B or 243 Am with 18 O |
In 1934, the German chemist Ida Noddack published a paper on three gaps in the Periodic Table of the Elements, which were later filled with the elements Francium , Astat and Promethium . As if by the way, she noted that it was conceivable that when heavy nuclei were bombarded with neutrons, these nuclei would disintegrate into several larger fragments . But not only that. It is also conceivable that elements with ordinal numbers Z> 92, i.e. transuranic elements, could be formed.
In fact, Edwin M. McMillan and Philip H. Abelson first synthesized the first non-naturally occurring actinoid nuclides 239 U, 239 Np and 239 Pu in 1940 by bombarding uranium with neutrons.
Since no nuclear reactor was in operation in 1940, the neutrons could only come from one neutron source .
Although a plutonium isotope is ultimately formed in this nuclear reaction , plutonium has probably not yet been detected because of the low yield. The year 1941 is considered to be the year of the discovery of plutonium, as the table Discovery of the transuranic elements shows.
Plutonium was discovered by the Americans Glenn T. Seaborg , J. W. Kennedy , E. M. McMillan , Michael Cefola and Arthur Wahl . At the end of 1940 they produced the plutonium isotope 238 Pu by bombarding the uranium isotope 238 U with deuterons that had been accelerated in a cyclotron . After clear evidence for element 94 had been provided, it was named plutonium in 1941 . The name was obvious because the two predecessor elements were named after the planets Uranus and Neptune. Details about the nuclear reactions can be found in the article Plutonium .
In order for a transmutation with electrically charged particles such as deuterons to take place, these particles must be accelerated to an energy sufficient to overcome the Coulomb barrier of uranium nuclei or at least to tunnel through it . This was possible for the first time with a cyclotron . The first weighable amount of plutonium of about 4 µg was isolated in 1942.

In late 1942, the first Chicago Pile nuclear reactor went into operation. With nuclear reactors, comparatively larger quantities of the elements plutonium and americium could be obtained, which served as target material. In connection with charged particles, with accelerated α-particles , the nuclides of the elements curium, berkelium and californium were discovered. The advantage of the process, the bombardment of accelerated charged particles at lighter actinides, is that massive, low-neutron nuclides can also be obtained that are not formed by neutron irradiation.
The most effective method to produce synthetic actinides is the transmutation of uranium or thorium nuclides in the nuclear fuel of a nuclear reactor by neutron capture or (n, 2n) reactions. This method is limited to actinide nuclides that are not too massive, for example up to mass numbers of A = 252. In terms of calculation (see below), only nuclides up to A <248 are usually included.
Americium, for example, was discovered in a two-step process. In the first stage, synthetic actinides are formed in a nuclear reactor, for example 239 Pu. After the nuclear fuel has been extracted, plutonium is chemically extracted by reprocessing. Then the plutonium is irradiated with neutrons again in the reactor or by means of a source. The currently operated 85 MW High-Flux-Isotope Reactor at Oak Ridge National Laboratory in Tennessee, USA is specially designed for the production of transcurium elements (Z> 96).
The massive elements Einsteinium and Fermium were brought to our earth by the test of the first American hydrogen bomb, Ivy Mike , on November 1, 1952 in the Eniwetok Atoll . Only a few weeks later they were discovered completely unexpectedly on filter paper and in debris on coral at the Lawrence Berkeley National Laboratory , which was not involved in the secret weapon development. In the hydrogen bomb explosion, up to 16 neutrons were captured by a core of 238 U. This intermediate nucleus disintegrated very quickly via a chain of beta decays into nuclides of the previously unknown elements. The uranium came from the casing of the hydrogen bomb, which consisted of five tons of natural uranium.
For reasons of military secrecy, the results were initially not allowed to be published. In order to secure the priority of the discovery of the two new elements, heavy ion reactions were successfully carried out in parallel . 238 U was bombarded with 14 N ions generated on a cyclotron. In this way, Einsteinium was first synthesized and the publication referred to the discovery of 1952. A similar procedure was followed with fermium, which was produced by bombarding 239 Pu with 14 N ions.
As the table shows, heavy ion reactions also led to the elements Mendelevium, Nobelium and Lawrencium with atomic numbers 101 to 103. The elements with higher atomic numbers were also synthesized with heavy ion reactions.
Formation and extraction in the nuclear reactor
As far as actinides are concerned, the nuclear reactor occupies a prominent position not only because it could not be operated without actinides, but also because it is only within a nuclear reactor that it is possible to form larger, weighable amounts of "higher" actinide nuclides. This section describes which actinide nuclides they are and in which mass fraction (relative to the original heavy metal mass) they are formed.
In a nuclear reactor, large amounts of actinides are introduced in the form of nuclear fuel at the start of operation, for example uranium enriched with 235 U. Actinide masses in the order of 100 t are obtained in a power reactor. In addition to the desired release of energy through nuclear fission, synthetic "higher" actinides are generated from this nuclear fuel through transmutation .
Actinide nuclides in a nuclear reactor
The figure nuclide map: formation and decay of actinides in a nuclear reactor is a nuclide map in the arrangement according to Segrè . This means that the number of neutrons increases to the right and the number of protons increases as it increases. In order to use the drawing area sensibly, the nuclide path is divided at the red point.
Each square in the figure represents an actinide nuclide that can occur in a nuclear reactor. The figure also shows the network of formation and decay of actinide nuclides triggered by the capture of free neutrons and other nuclear reactions. A similar scheme can be found in a paper from 2014. It contains the isotopes of thorium and protactinium, which play a major role in molten salt reactors, for example , and the isotopes of the elements berkelium and californium are not included.
The formation of actinide nuclides is primarily characterized by:
- Neutron capture reactions (n, γ), which are shown in the figure by a short right arrow.
- However, the (n, 2n) reactions and the less common (g, γ) reactions, both of which are marked by a short arrow to the left, are also taken into account.
- The (n, 3n) reaction occurs even more rarely and is only triggered by fast neutrons, which is represented in the figure with an example, marked by a long left arrow.
In addition to these neutron or gamma-induced nuclear reactions, the radioactive conversion of the actinide nuclides also has an effect on the nuclide inventory in a reactor at a given point in time (burn-up state). These types of decay are marked in the figure by diagonal arrows.
The beta-minus decay , marked with upward-pointing diagonal arrows, plays a major role in the balance of the particle densities of the nuclides . The squares of the nuclides of this type of decay have a light blue fill color in the nuclide map. Two nuclides are only partially beta-active. The nuclide with a pink background, 236 Np, is converted to 86% by electron capture and 14% by beta-minus decay (light blue corner). The ground state of 242 Am (pink corner) also shows two types of decay, but in almost the opposite relationship (83% beta-minus decay, 17% electron capture ). This nuclide also has a long-lived metastable state ( highlighted in white), which is usually symbolized by 242m1 Am. Nuclides with positron emissions (beta plus decays) do not occur in a nuclear reactor.
The actinide nuclides, which transform spontaneously with the emission of α-particles , have been given a yellow fill color in the nuclide map in the figure. Due to the long half-lives (T 1/2 ) in the formation and decay of the actinides during the duration of the fuel in a power reactor (max. Approx. 3 years), the α-decay plays almost no role. Exceptions are the two relatively short-lived nuclides 242 Cm (T 1/2 = 163 d) and 236 Pu (T 1/2 = 2.9 a). Only in these two cases is the α-decay marked by long arrows pointing downwards on the nuclide map.
All half-lives shown in the figure are the current evaluated nuclear data NUBASE2012, accessed via the JANIS 4 nuclear data viewer. Some half-lives are rounded.
On the importance of combustion programs
The composition of the nuclides in the nuclear fuel is only known exactly when the reactor is first started up. However, for every point in time (burn-up state) it is necessary to know basic physical quantities such as the neutron flux . The basic physical quantities also include the particle densities and mass densities of all actinide nuclides formed in the reactor. This applies to both the nuclides initially introduced (or whatever is still present) and the nuclides formed during reactor operation. It is not possible to measure the actual particle densities (and mass densities) of the actinide nuclides as a function of the burn-up during operation. Only after the nuclear fuel has been discharged can these quantities be examined chemically or by mass spectrometry in principle. That is very time-consuming. A calculation that accompanies the operational sequence of a nuclear reactor is therefore of great importance.
The development of the particle densities (and mass densities) of nuclides in a nuclear reactor is calculated in a simplified manner in so-called burnup programs depending on the mean burnup , for example:
- ORIGEN, the first worldwide program for calculating nuclide formation in relation to burn-up from 1973,
- OrigenArp, a program for calculating the particle densities of nuclides depending on the burnup from 2010, which is also integrated into the SCALE program system (see below).
For a detailed analysis, highly complex reactor program systems ( neutron transport programs ) are used, the scope of which goes far beyond those of the programs mentioned above and whose application requires a long training period, for example:
- SCALE, a large program system for different neutron physical calculations, so u. a. also for burn-up and shielding bills ,
- HELIOS, a cell and burn-off program system for calculations in neutron transport approximation.
In the latter program systems, in addition to the initial material composition, geometric details of reactor components (cells) must also be specified. From time to time, such calculations are compared with the results of chemical and mass spectrometric analysis of discharged nuclear fuel and, if necessary, more precise measurements of still uncertain nuclear data or more precise calculation methods are initiated.
Development of the masses of actinides in the nuclear reactor
The figure Development of the masses of the actinides ... shows the increase or decrease in the masses of the 14 most common actinide nuclides in a pressurized water reactor that is operated with enriched uranium. The numerical values were calculated for a larger fuel cell depending on the burnup (the specific energy release). The calculations were carried out in 2005 using the HELIOS 1.8 program system. 4% was chosen as the initial concentration of the nuclide 235 U for this example. The points on the curves in the figure mark the increments in the burnup calculation. The step size is initially smaller in order to more precisely capture those fission products that reach their saturation very quickly. This is especially true of the strong neutron absorbers 135 Xe and 149 Sm. A similar figure, restricted to uranium and plutonium isotopes, can be found in Paul Reuss' textbook Neutron Physics .
The mass of each nuclide is divided by the mass of heavy metal initially used, the mass of uranium. The mass fractions of all nuclides that were initially present (three uranium nuclides) or that are formed with a mass of at least 10 g per ton of heavy metal used after a burn-up of a maximum of 80 MWd / kg are shown.
As the figure shows, the masses of the three uranium isotopes 238 U, 235 U and 234 U that were initially present decrease monotonically with increasing burnup. At the same time, the masses of the higher actinides increase almost linearly (note the logarithmic scaling of the ordinate). Of all synthetic actinides, the mass of the nuclide 239 Pu increases the most. This also increases the number of splits in the nuclide 239 Pu. From a burn-up of approx. 45 MWd / kg, its mass decreases again slightly.
Would be the ordinate down to a mass fraction of at least 1 g per tonne of lower heavy metal, come in the figure from a Abrand of approximately 45 MWd / kg nuclide 242m1 Am and from a Abrand of approximately 60 MWd / kg nuclide 243 cm.
In summary: In a pressurized water reactor with uranium fuel elements (without MOX fuel elements ), a maximum of 13 synthetic actinide nuclides are formed from the originally present actinide nuclides 235 U and 238 U (and a small proportion of 234 U) within the normal operating times, their proportion is greater than 1 g per ton of starting weight heavy metal (SM), i.e. 1 ppm . These are the nuclides 236 U, 237 Np, 238 Pu, 239 Pu, 240 Pu, 241 Pu, 242 Pu, 241 Am, 242m1 Am, 243 Am, 242 cm, 243 cm and 244 cm. Nuclides of the elements berkelium and californium are also formed in a nuclear reactor, but only in very small quantities.
As mentioned, the actinides can be extracted from discharged fuel by chemical processing. The mass fraction of curium, for example, is approx. 0.00024 with a (currently common) burn-up of 60 MWd / kg:
- ,
where the mass of the curium and the starting mass of the heavy metal mean. In a power reactor, the initial heavy metal mass is approx. , Distributed over 193 fuel elements. Assume that all fuel elements that have reached this burn-up state have been unloaded. Hence the mass of the curium
- .
In the entire reactor, about 24 kg of curium were formed in the fuel during this average burnup.
It should be noted that power reactors are not operated to obtain actinides, but to split as many actinides as possible and release energy. The total mass of all actinides is reduced by nuclear fission, with an average burn-up of 60 MWd / kg by a total of only approx. 6%. This can be found in the bulk of the fission products.
properties
Nuclear properties
The prominent position of the actinides, one thinks of their importance for the release of nuclear energy and for nuclear weapons , are determined by the properties of their atomic nuclei .
- All actinide nuclides are radioactive.
- All actinide nuclides are neutron-induced fissile, albeit with very different cross -sections , which also depend very strongly on the kinetic energy of the neutrons.
- The four actinide nuclides 232 Th, 234 U, 235 U and 238 U occur naturally. Their squares are highlighted in the above nuclide map by a thicker border. With the exception of 234 U, these are primordial nuclides , i.e. nuclides that were already present when the earth was formed and have not yet completely decayed. The naturally occurring, extremely rare primodial plutonium nuclide 244 Pu does not play a role in the nuclear reactor. Its mass fraction in some ores is 10 −18 .
- In the year 2000 more than 200 synthetically produced actinide nuclides were known. Most have short half-lives. Only 45 have half-lives T 1/2 > 40 d.
- 41 actinide nuclides are believed to be capable of a self-sustaining chain reaction . Other sources assume fewer actinide nuclides for which there is a critical mass .
- For the six actinoid nuclides 233 U, 235 U, 238 U, 239 Pu, 240 Pu and 241 Pu, the cross -sections are known relatively precisely, for all others the nuclear data are less precise. However , these inaccuracies have hardly any effect on criticality calculations . The less mass of a nuclide is in the nuclear reactor, the less the effect of incorrect cross sections on such calculations.
Classic physical properties
Some physical properties of the actinoid elements can be found under the keyword of the names of the elements. The prerequisite for being able to measure classical physical properties, for example crystal structure , mass density, melting point , boiling point or electrical conductivity , is that the element can be extracted in weighable quantities. The number of physical properties actually measured decreases rapidly as the atomic number of the element increases. For example, californium is the last actinoid element of which mass density could be measured.
Regarding the atomic physics of actinides, it should be noted:
- As mentioned above, all actinides are heavy metals.
- Some actinides are pyrophoric in a finely divided state .
- Like the lanthanides, actinides belong to the inner transition elements or f-block elements , since the f- subshells in these rows are filled with electrons.
Chemical properties
All actinides form triply charged ions , like actinium they are understood as a subgroup of the 3rd subgroup . The “lighter” actinides (thorium to americium) occur in a larger number of oxidation numbers than the corresponding lanthanoids.
Colors of actinide ions in aqueous solution
| Oxidation number | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 |
| +3 |
Ac 3+ colorless |
(Th 3+ ) deep blue |
(Pa 3+ ) blue-black |
U 3+ purple |
Np 3+ purple-violet |
Pu 3+ deep blue |
On the 3+ yellow-pink |
Cm 3+ colorless |
Bk 3+ yellow-green |
Cf 3+ green |
It's 3+ pale pink |
Fm 3+ |
Md 3+ |
No 3+ |
Lr 3+ |
| +4 |
Th 4+ colorless |
Pa 4+ pale yellow |
U 4+ emerald green |
Np 4+ yellow-green |
Pu 4+ orange brown |
On the 4+ yellow-red |
Cm 4+ pale yellow |
Bk 4+ beige |
Cf 4+ green |
||||||
| +5 |
PaO 2 + colorless |
UO 2 + pale purple |
NpO 2 + green |
PuO 2 + pink |
AmO 2 + yellow |
||||||||||
| +6 |
UO 2 2+ yellow |
NpO 2 2+ pink-red |
PuO 2 2+ old rose |
AmO 2 2+ lemon yellow |
|||||||||||
| +7 |
NpO 2 3+ deep green |
PuO 2 3+ blue-green |
(AmO 6 5− ) dark green |
links
The properties relate to the most common or most stable isotope.
Oxides
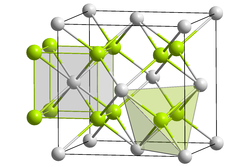
The tetravalent oxides of the actinides crystallize in the cubic crystal system ; the structure type is the CaF 2 type ( fluorite ) with the space group Fm 3 m (space group no. 225) and the coordination numbers An [8], O [4].
| Actinide dioxides | |||||||||
| Surname |
Thorium (IV) oxide |
Protactinium (IV) oxide |
Uranium (IV) oxide |
Neptunium (IV) oxide |
Plutonium (IV) oxide |
Americium (IV) oxide |
Curium (IV) oxide |
Berkelium (IV) oxide |
Californium (IV) oxide |
| CAS number | 1314-20-1 | 12036-03-2 | 1344-57-6 | 12035-79-9 | 12059-95-9 | 12005-67-3 | 12016-67-0 | 12010-84-3 | 12015-10-0 |
| Molecular formula | ThO 2 | PaO 2 | UO 2 | NpO 2 | PuO 2 | AmO 2 | CmO 2 | BkO 2 | CfO 2 |
| Molar mass | 264.04 g mol −1 | 263.04 g mol −1 | 270.03 g mol −1 | 269.05 g mol −1 | 276.06 g mol −1 | 275.06 g mol −1 | 279.07 g mol −1 | 279.07 g mol −1 | 283.08 g mol −1 |
| Melting point | 3390 ° C | 2878 ° C | 2600 ° C | 2400 ° C | 1000 ° C (dec.) | 380 ° C (dec.) | |||
| boiling point | 4400 ° C | 2800 ° C | |||||||
| Structural formula |
 __ An 4+ __ O 2− __ An 4+ __ O 2−
|
||||||||
| Space group | Fm 3 m (No. 225) | ||||||||
| Coordination numbers | An [8], O [4] | ||||||||
| Lattice constants | 550.5 pm | 547 pm | 543 pm | 540 pm | 533 pm | 536 pm | 533 pm | 531 pm | |
Halides
The trivalent chlorides of the actinides crystallize in the hexagonal crystal system . The structure of uranium (III) chloride is the lead structure for a number of other compounds. In this, the metal atoms are surrounded by nine chlorine atoms each. The coordination polyhedron is a triple-capped, trigonal prism , as is often found in the later actinides and lanthanides . It crystallizes in the hexagonal crystal system in the space group P 6 3 / m (space group no. 176) and two formula units per unit cell .
| Trivalent chlorides of the actinides | |||||||
| Surname | Uranium (III) chloride |
Neptunium (III) chloride |
Plutonium (III) chloride |
Americium (III) chloride |
Curium (III) chloride |
Berkelium (III) chloride |
Californium (III) chloride |
| CAS number | 10025-93-1 | 20737-06-8 | 13569-62-5 | 13464-46-5 | 13537-20-7 | 13536-46-4 | 13536-90-8 |
| Molecular formula | UCl 3 | NpCl 3 | PuCl 3 | AmCl 3 | CmCl 3 | BkCl 3 | CfCl 3 |
| Molar mass | 344.39 g mol −1 | 343.41 g mol −1 | 350.32 g mol −1 | 349.42 g mol −1 | 353.43 g mol −1 | 353.43 g mol −1 | 357.44 g mol −1 |
| Melting point | 837 ° C | 800 ° C | 767 ° C | 715 ° C | 695 ° C | 603 ° C | 545 ° C |
| boiling point | 1657 ° C | 1767 ° C | 850 ° C | ||||
| Structural formula |
 __ An 3+ __ Cl - __ An 3+ __ Cl -
|
||||||
| Space group | P 6 3 / m (No. 176) | ||||||
| Coordination numbers | An [9], Cl [3] | ||||||
| Lattice constants | a = 745.2 pm c = 432.8 pm |
a = 740.5 pm c = 427.3 pm |
a = 739.4 pm c = 424.3 pm |
a = 738.2 pm c = 421.4 pm |
a = 726 pm c = 414 pm |
a = 738.2 pm c = 412.7 pm |
a = 738 pm c = 409 pm |
See also
Individual evidence
- ↑ Wolfgang Liebscher, Ekkehard Fluck: The systematic nomenclature of inorganic chemistry. Springer, Berlin 1999, ISBN 3-540-63097-X .
- ^ Neil G. Connelly (Red.): Nomenclature of inorganic chemistry - IUPAC recommendations 2005. Royal Society of Chemistry, Cambridge 2005, ISBN 0-85404-438-8 .
- ↑ a b c Janis 4 - Java-based Nuclear Data Information System .
- ↑ Norman N. Greenwood, Alan Earnshaw: Chemistry of the elements . 2nd ed., Repr. Elsevier Butterworth-Heinemann, Amsterdam, Heidelberg 2005, ISBN 0-7506-3365-4 , p. XXII, 1341, p. 1250 ff . (English).
- ↑ Ida Noddack: The Periodic System of the Elements and its gaps , in: Angewandte Chemie , 1934 , 47 (20), pp. 301-305 ( doi: 10.1002 / ange.19340472002 ).
- ^ E. McMillan, PH Abelson: Radioactive Element 93 , in: Physical Review , 1940 , 57 , pp. 1185-1186 ( doi: 10.1103 / PhysRev.57.1185.2 ).
- ↑ BB Cunningham, LB Werner: The First Isolation Of Plutonium. In: Journal of the American Chemical Society . 71 (5), 1949, pp. 1521-1528 ( doi: 10.1021 / ja01173a001 ).
- ↑ a b c Matthew W. Francis et al. : Reactor fuel isotopics and code validation for nuclear applications . ORNL / TM-2014/464, Oak Ridge, Tennessee 2014, pp. 11 (xv, 89 p., Ornl.gov [PDF; accessed on November 18, 2017]).
- ^ High Flux Isotope Reactor , Oak Ridge National Laboratory; accessed on November 18, 2017.
- ^ Albert Ghiorso: Einsteinium and Fermium , Chemical & Engineering News, 2003.
- ↑ a b The heavy metal mass is not easy to find for every power reactor. In the article Emsland nuclear power plant , the heavy metal mass is given as 103 t, distributed over 193 fuel elements . This should also approximately apply to the other power reactors of the convoy type .
- ^ Audi, G., FG Kondev, M. Wang, B. Pfeiffer, X. Sun, J. Blachot, and M. MacCormick: The NUBASE2012 evaluation of nuclear and decay properties . In: Chinese Physics C . tape 36 , no. 12 , 2012, p. 1157-1286 .
- ↑ MJ Bell: ORIGEN - The ORNL Isotope Generation and Depletion Code . Oak Ridge National Laboratory, Oak Ridge, Tenn. 1973 (148 pp.).
- ↑ SM Bowman, IC Gauld: OrigenArp Primer: How to perform isotopic depletion and decay calculations with SCALE / ORIGEN . ORNL / TM-2010/43, Oak Ridge, Tennessee 2010 ( ornl.gov [PDF; accessed November 18, 2017]).
- ↑ Bradley T. Rearden: SCALE Code System . Oak Ridge, Tennessee 2016 (2712 pp. Ornl.gov [PDF; accessed November 18, 2017]).
- ↑ Stamm'ler, Rudi JJ et al .: HELIOS Methods: Version 1.8 . Studsvik Scandpower 2003 (192 pages).
- ↑ RK: PWR-Calculations with the Code-System HELIOS 1.8 , Studsvik 2005 International User's Group Meeting, Charlotte, NC, USA, June 1-3, 2005.
- ^ Paul Reuss: Neutron physics . EDP Sciences, Les Ulis, France 2008, ISBN 978-2-7598-0041-4 , pp. 325 (xxvi, 669 p., Limited preview in Google Book Search [accessed November 18, 2017]).
- ↑ a b c d RQ Wright, WC Jordan, RM Westfall: Critical Masses of Bare Metal Spheres Using SCALE / XSDRN . In: Proceedings of the Annual Meeting of the American Nuclear Society . 2000, p. 167 . The summary can be found in the INIS repository https://inis.iaea.org/search/search.aspx?orig_q=RN:31056505
- ↑ Guttmann, Hengge: Inorganic Chemistry . VCH, Weinheim / New York / Basel / Cambridge 1990.
- ^ AF Holleman , E. Wiberg , N. Wiberg : Textbook of Inorganic Chemistry . 102nd edition. Walter de Gruyter, Berlin 2007, ISBN 978-3-11-017770-1 , p. 1956.
- ↑ dtv-Atlas zur Chemie 1981 , part 1, p. 224.
- ↑ a b The values of the atomic and physical properties are taken from www.webelements.com , unless otherwise stated .
- ^ A b Lester R. Morss, Norman M. Edelstein, Jean Fuger (Ed.): The Chemistry of the Actinide and Transactinide Elements: Vol. 3 , 2006 , Springer, ISBN 1-4020-3555-1 .
literature
- Lester R. Morss, Norman M. Edelstein, Jean Fuger (Eds.): The Chemistry of the Actinide and Transactinide Elements . Springer, Dordrecht 2006, ISBN 1-4020-3555-1 :
- Harold W. Kirby, Lester R. Morss: Actinium , pp. 18-51; doi : 10.1007 / 1-4020-3598-5_2 .
- Mathias S. Wickleder, Blandine Fourest, Peter K. Dorhout: Thorium , pp. 52-160; doi : 10.1007 / 1-4020-3598-5_3 .
- Boris F. Myasoedov, Harold W. Kirby, Ivan G. Tananaev: Protactinium , pp. 161-252; doi : 10.1007 / 1-4020-3598-5_4 .
- Ingmar Grenthe, Janusz Drożdżynński, Takeo Fujino, Edgar C. Buck, Thomas E. Albrecht-Schmitt, Stephen F. Wolf: Uranium , pp. 253–698; doi : 10.1007 / 1-4020-3598-5_5 .
- Zenko Yoshida, Stephen G. Johnson, Takaumi Kimura, John R. Krsul: Neptunium , pp. 699-812; doi : 10.1007 / 1-4020-3598-5_6 .
- David L. Clark, Siegfried S. Hecker, Gordon D. Jarvinen, Mary P. Neu: Plutonium , pp. 813-1264; doi : 10.1007 / 1-4020-3598-5_7 .
- Wolfgang H. Runde, Wallace W. Schulz: Americium , pp. 1265-1395; doi : 10.1007 / 1-4020-3598-5_8 .
- Gregg J. Lumetta, Major C. Thompson, Robert A. Penneman, P. Gary Eller: Curium , pp. 1397-1443; doi : 10.1007 / 1-4020-3598-5_9 .
- David E. Hobart, Joseph R. Peterson: Berkelium , pp. 1444-1498; doi : 10.1007 / 1-4020-3598-5_10 .
- Richard G. Haire: Californium , pp. 1499-1576; doi : 10.1007 / 1-4020-3598-5_11 .
- Richard G. Haire: Einsteinium , pp. 1577-1620; doi : 10.1007 / 1-4020-3598-5_12 .
- Robert J. Silva: Fermium, Mendelevium, Nobelium, and Lawrencium , pp. 1621-1651; doi : 10.1007 / 1-4020-3598-5_13 .
- AF Holleman , E. Wiberg , N. Wiberg : Textbook of Inorganic Chemistry . 102nd edition. Walter de Gruyter, Berlin 2007, ISBN 978-3-11-017770-1 , pp. 1948-1976.
- James E. Huheey: Inorganic Chemistry . de Gruyter, Berlin 1988, ISBN 3-11-008163-6 , pp. 873-900.
- Norman N. Greenwood, Alan Earnshaw: Chemistry of the Elements . 1st edition. VCH, Weinheim 1988, ISBN 3-527-26169-9 , pp. 1601-1641.
- dtv-Atlas zur Chemie , Part 1. 1981, pp. 222-229.
![{\ mathrm {^ {{238}} _ {{\ 92}} U \ + \ _ {{0}} ^ {{1}} n \ \ longrightarrow \ _ {{\ 92}} ^ {{239} } U \ {\ xrightarrow [{23 \ min}] {\ beta ^ {-}}} \ _ {{\ 93}} ^ {{239}} Np \ {\ xrightarrow [{2,355 \ d}] {\ beta ^ {-}}} \ _ {{\ 94}} ^ {{239}} Pu}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6604de3d102be4a0a9b26d5b57873a6eeca17ae0)






